Осцилляторлық өрнектеу арқылы чармоний мен боттомоний мезондарының спектроскопиясы: конституенттік массалар, спин әсерлесулері, релятивистік түзетулер және киральды симметрияның бұзылуы


резюме
Магистерлік диссертация кіріспе, 5 бөлім, 140 формула, 6 сурет, 10 кесте, қорытынды, қосымша және қолданылған әдебиеттер тізімінен құралған барлығы 79 беттен тұрады.
Негізгі сөздер : адрондар, боттомоний, чармоний, мезон, кварк, гамильтониан, осцилляторлық өрнектелу, кулондық потенциал, энергетикалық спектр, полярланған тұзақ, релятивистік түзету, байланысқан күй, спин-спиндік және спин-орбиталдық әсерлесу, криалдық симметрия.
Жұмыстың мақсаты : жеңіл - ауыр кварктардан тұратын мезондардың қасиетін спин-спиндік, спин-орбиталдық әсерлесулерді ескеріп анықтау, чармоний мен боттомонийді зерттеу, кириалды симметрияның бұзылуын ескергендегі мезондардың қасиеттерін анықтау.
Зерттеу әдістері: теориялық зерттеулер осцилляторда өрнектелу әдісі арқылы жүргізілді.
Қолдану аймағы: элементар бөлшектер мен атомдық ядро физикасында, ядролық физика, іргелі әрекеттесулердегі өрістің кванттық теориясында, және де, берілген қасиетімен жаңа материал жасауда қолданылады.
Жаңалығы: әдістеме бойынша кварктардың байланыс күйінің конституенттік массасы аналитикалық жолмен анықталды. Бөлшектердің конституенттік массасы еркін күйлердің массасынан өзгеше екені көрсетілді. Псевдоскаляр мезондардың массалық спектрі және релятивистік түзету ескеріліп, мезондардың қасиеті анықталды, киральды симметрияның бұзылуы ескеріле отырып, қайта қаралды. Боттомоний мен чармонийдің қасиеттері зерттелінді. Есептеулер жоғары дәлдікпен жүргізілді.
резюме
Диссертация состоит из введения, 5 разделов, 140 формул, заключения, списка использованных литератур и приложения. Работа изложена на 79 страницах печатного текста.
Ключевые слова: адроны, боттомоний, чармоний, мезон, кварк, гамильтониан, осцилляторное представление, кулонный потенциал, энергетический спектр, поляризованная петля, релятивистская поправка, связанная состояние, спин - спиновое и спин - орбитальное взаимодействие, киральная симметрия.
Цель диссертационный работы: определение свойств мезонов состоящих из тяжелых и легких кварков с учетом спин - спинного, спин - орбитального взаимодействия, исследование свойств чармиония и боттомония, определение свойств мезонов при нарушении киральной симметрии.
Метод исследования: теоретические исследования с применением осцилляторного представления.
Область применения: физика элементарных частиц и атомного ядра, ядерная физика, квантовая теория поля в фундаментальных взаимодействиях и для получения новых материалов.
Новизна работы: конституентная масса связанных состояний кварков определена аналитическим путем с помощью осцилляторного метода. Выяснено что, конституентная масса частиц отличается от массы свободного состояния. Свойства мезонов определены и пересмотрены с учетом массовых спектров псевдоскалярных мезонов и релятивистских поправок, а также с учетом нарушения киральной симметрии. Исследованы свойства боттомония и чармония. Расчеты произведены с высокой точностью.
SUMMARY
The thesis consists of an introduction, 5 chapters, 140 formulas, conclusions, bibliography and annexes. The work presented on 79 pages of printed text.
Keywords: hadrons, bottomonium, charmonium, meson quark Hamiltonian, the oscillatory representation, pendants potential, energy spectrum, polarized loop, relativistic correction associated state, the spin - spin and spin - orbit interaction, chiral symmetry.
The aim of the thesis: the definition of the properties of mesons consisting of weight and light quarks, taking into account the spin - spinal cord, spin - orbit interaction, the study of the properties charmioniya and bottomonium, the definition of the properties of mesons in violation of chiral symmetry.
Method of research: theoretical studies using the oscillator representation.
Scope: elementary particle physics and nuclear physics, nuclear physics, quantum field theory of fundamental interactions and for new materials.
The novelty of the work: the constituent mass of the bound states of quarks is determined analytically by using the oscillator method. It was found that the constituent mass of the particles is different from the mass of a free state. The properties of mesons are defined and revised to reflect the mass spectra of pseudoscalar mesons, and relativistic corrections, as well as the chiral symmetry breaking. The properties of charmonium and bottomonium. Calculations are made with high accuracy.
Мазмұны
Кіріспе . . . 8
I. РЕЛЯТИВИСТІК БАЙЛАНЫС КҮЙІНІҢ МАССАЛЫҚ СПЕКТРІН АНЫҚТАУ . . . 13
1. 1Релятивистік әсерлесу сипаттамасын ескере отырып байланыс күйдің массалық спектрін сипаттайтын үлгі. . . . . 13
1. 2 Әсерлесу гамильтонианына пертурбативтік емес түзетуді енгізу . . . 19
II. КРИАЛДЫ СИММЕТРИЯНЫҢ БҰЗЫЛУЫ . . . 22
III. ЖЕҢІЛ-АУЫР КВАРЫКТАРДАН ТҰРАТЫН МЕЗОНДАРДЫ ЗЕТТЕУ . . . 34
3. 1 Сызықты өсетін потенциалдың энергетикалық спектрін анықтау . . . 35
3. 2 Спин - спиндік әсерлесудің мезондар массасына тигізетін үлесі . . . 40
3. 3 Мезондардың массалық спектрін спин-cпиндік, спин-орбиталдық әсерлесулерді ескеріп анықтау . . . 41
IV. АУЫР КВАРЫКТАРДАН ТҰРАТЫН МЕЗОНДАРДЫҢ ТӘЖІРИБЕДЕН АНЫҚТАЛҒАН СИПАТТАМАСЫ. . 44
4. 1 Чармоний . . 50
4. 2 Боттомоний . . . 54
4. 3 Релятивистік гамильтониандық жуықтау шеңберіндегі боттомонидың массалық спектрі . . . …. . 57
4. 4 Қысқа қорытынды . . . …59
V. ауыр және жеңіл кварктерден тұратын мезондардың спектроскопиясы . . . 61
5. 1Мезондарың массасына толық гамильтонианды енгізу арқылы кварктардың массасын және конституентті массын анықтау . . . 62
5. 2 Мезондардың массасына меншікті энергияның қосатын үлесі . . . 68
VI. ҚОыРТЫНДЫ . . . …74
VII. ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕРТІЗІМІ. . . . …. 75
VIII. ҚОСЫМША . . . . . . . . . …. 77
АНЫҚТАМАЛАР
Осы диссертациялық жұмыста келес анықтамалары бар терминдер қолданады:
скалярлық өрістің кванттық теорияларының идеялары мен әдістерінде негізі салынған әдіс және бұл әдіс энергетикалық спектрды анықтауға арналған.
Қысқартулар мен белгілеулер
КМ Кванттық механика
КЭД Кванттық электродинамика
КЕЭД Кванттық емес электродинамика
ӨКТ Өрістің кванттық теориясы
РЕӨКТ Релятивистік емес Өрістің кванттық теориясы
РЕКМ Релятивистік емес кванттық механика
ЛЕКМ Локалды емес кванттық механика
ТФ Толқындық функция
ОК Осцилляторлық көрініс
ОӨ Осцилляторлық өрнек
ШТ Шредингер теңдеуі
КХД Кванттық хромодинамика
БЭ Байланыс энергиясы
 Әсерлесу гамильтонианы
Әсерлесу гамильтонианы
 Еркін осциллятордың гамильтонианы
Еркін осциллятордың гамильтонианы
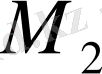 Келтірілген масса
Келтірілген масса
 Скаляр бөлшектің массасы
Скаляр бөлшектің массасы
 Гамма функциясы
Гамма функциясы
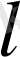 Орбиталдық кванттық сан
Орбиталдық кванттық сан
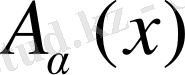 Калибрлік өріс
Калибрлік өріс
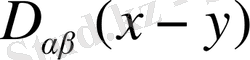 Калибрлі өрістің пропогаторы
Калибрлі өрістің пропогаторы
 Байланыс тұрақтысы
Байланыс тұрақтысы
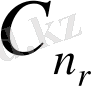 Equation. 3
Нормаланданған констант
Equation. 3
Нормаланданған констант
 Энергетикалық спектр
Энергетикалық спектр
 Осциллятор жиілігі
Осциллятор жиілігі
 Лапласиан
Лапласиан
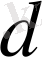 Кеңістіктің өлшемділігі
Кеңістіктің өлшемділігі
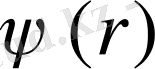 Толқындық функция
Толқындық функция
Кіріспе
Қазіргі кезде кванттық денелердің қалыптасу құрылымы мен механизмі жөнінде мынандай көріністер бар: байланыс күйлері фермиондардан тұрады, ал бұл фермиондардың арасындағы әсерлесу базондардың алмасуы арқылы іске асады. Атомдық, ядролық және адрондық болатын күйлерде келесі түрде іске асырылады. Электрондар мен ядродан тұратын атомдық құрылымда мұндай базондар фотондар, нуклондардан тұратын ядролық құрылымда π-мезон және кварктардан тұратын адрондық құрылымда- глюондар болып табылады. Сонымен, өрістің кванттық теориясы (ӨКТ) шеңберінде кванттық жүйелердің құрылуы бірыңғай жолмен түсіндіріледі деп көруге болады. Байланысқан күйлердің құрылу механизмін бірыңғай сипаттау үшін релятивистік инварианттылықтың, яғни Лоренц түрлендірулеріне инварианттық шартының орындалуы қажет немесе кванттық жүйелердің қасиетін сипаттайтын негізгі заңдар ковариантты. Қазіргі кезде әсерлесудің релятивистік сипаты өрістің кванттық теориясының аумағында сипатталады [1] . Өрістің кванттық теориясында Лоренц инварианттылығы орындалады. Бірақ, жүйенің құрылуын сипаттаған кезде, яғни өрістің кванттық теориясының аумағында байланысқан күйлердің энергетикалық спектрін анықтаған кезде, біз белгілі қиыншылықтарға кездесеміз [1] немесе өрістің кванттық теориясында байланыс күйдің энергетикалық спектрі деген түсінік дәл жоқ.
Бір жағынан байланысқан күйлердің энергетикалық спектрі жақсы дәлдікпен релятивистік емес кванттық механиканың (КМ) аумағында анықталады. Бірақ релятивистік емес кванттық механикада релятивистік инварианттылық шарты орындалмайды.
Өрістің кванттық теориясының аумағында байланысқан күйлердің энергетикалық спектрін сипаттауға Швингер [2] мен Бете-Солпетер [3] Грин функциясының коварианттық ұсынысын қолдануға әрекет еткен. Алынған теңдеу үлкен жетістік болғанмен, нақты байланысқан күйдің энергетикалық спектрін анықтау қиын, ал сандық нәтиженің дәлдігін жақсарту мүмкін емес. Бір жағынан белгілі, егер байланысқан күйлердің құрамын сипаттау кезінде массалық центр жүйесіне көшу тек релятивистік емес кванттық механиканың аумағында мүмкін. Сондықтан әсерлесудің релятивистік сипатын ескере отырып, байланысқан күйлердің энергетикалық спектрін анықтау және құрамын сипаттау қазіргі заманның бірден бір маңызды мәселелерінің бірі болып табылады.
Алайда, казіргі кездегі релятивистік ӨКТ- да байланысқан күйдің түзілуі және сипатталуы жақсы қойылған мәселелердің бірі болып табылмайды [1-3] . ӨКТ-сы жазық толқын күйіндегі бір бірінен өте үлкен қашықтықта орналасқан бос релятивистік бөлшектердің серпімді және серпімсіз ыдырауларын сипаттайды. Сонымен қатар, ӨКТ- ның қалыптасуы ығысу теориясы шеңберінде жүреді, яғни ешқандай байланысқан күйдің пайда болуы мүмкін болмайтын әсерлесу дәрежесінің жіктелуі. Сондықтан байланысқан күйге қойылған есебіміз қолда бар зерттеу әдістері жақсы жетілмеген ығысу теорясы шеңберінен шығып кетеді.
Байланыс күйінің энергетикалық спектрі әсерлесудің лайықты потенциялын таңдау кезіндегі релиятивистік емес кванттық механика (РЕМК) шеңберінде үлкен дәлдікпен анықталуы мүмкін екендігі белгілі. Байланыс күйлерін математикалық дұрыс сипаттауды беретін Шредингердің релятивистік емес теңдеуі әсерлесудің релятивистік сипатын ескеру керек болғандықтан жеткілікті болмайды. Өйткені заманауи атомдық [4] және адрондық [5] физикада алынған эксперименттік нәтижелерді сипаттау үшін релятивистік түзетулерді ескеру керек.
Олай болса нақты физика байланыс күйінің мәселелерін шешу қандайда бір математикалық шешімін ӨКТ негізінде құруды талап етеді. Осы мәселелерді шешуге бағытталған ізденістерді шартты түрде екі бағытқа бөлуге болады.
Бірінші бағыттың бастапқы нүктесі егер сәйкес кванттық сандармен екі бөлшектің байланысқан күйі бар болатын болса онда бұл бөлшектердің серпімді шашыраудың амплитудасы байланыс күйінің масса нүктесінде энергия бойынша жай полюсі бар болады деген пікір болып табылады. Осы идея негізінде квазипотенциялды теңдеулер [8] деп аталатын Бетте- Солпитер теңдеуі [3, 6, 7] қорытылды.
Келесі бағыт мына пікірге негізделген: релятивистік емес ШТ байланыс күйінің энергетикалық спектрін анықтау және зерттеудің сенімді құралы болып табылады. Бұл кезде нақты релятивистік түзетулер аз, сондықтан теориялық емес ӨКТ формализмнінен шығатын әсерлесудің релятивистік емес потенциялынан релятивистік түзетулерді алуға алып келеді. Бұл идея Бреит потенциалының негізінде жатыр [9] және Касвелл және Лепаждың [10] өрістің релятивистік емес кванттық теориясына тиімді. Бұл екі амалдарда бастапқы түзетулердің көзі ретінде шашырау матрицасы қолданылады. Авторлар [10] алдымен кванттық электродинамика шеңберінде релятивистік емес шекке тізбекке ауысу және қайта нормалдауды ескеріп сәйкес келетін Фейнман диаграмасымен шашырау матрицасы зерттелген яғни релятивистік түзетулері бар әсерлесу потенциялы анықталған. Нәтижесінде релятивистік түзетулері бар энергетикалық спектрді анықтауға арналған КЭД немесе релятивистік емес КЕЭД әдісі қорытылды. Кейіннен бұл әдіс [11] де жетілдірілді. Қазіргі кезде релятивистік түзетулер кулондық байланыс күйінің спектрімен қасиеттері КЕЭД шеңберінде анықталады. Бұл әдіс сондай- ақ жоғары дәлдікпен соңғы эксперименттік нәтижелерді сипаттайды. Бұл тәсілде ығысу теориясы бойынша тек төменгі дәрежелі жіктеумен шектеледі, ал жоғарғы дәрежелер аз түзетулер ретінде қарастырылады. Адрондық физикада кварктардың әсерлесу потенициялы кейбір физикалық болжамдардан алынады. Кварктардың феноменологиялық потенциалдық үлгілері [12-14] ауыр кварктардан тұратын адрондардың массалық спектрін жақсы сипаттайды. Жеңіл кварктардан тұратын адрондардың қаситетін зерттеу кезінде әсерлесудің релятивистік сипатын ескеру керек болады. Алайда қазіргі кезде кварктердің феноменологиялық үлгілерінде әсерлесудің релятивистік сипатын ескерудің жалпы қабылданған формуласы жоқ.
Соңғы бағыт аясында келесі идеяға негізделген тағы бір тәсіл бар. Гриннің кванттық-өріс функциясына арналған нақты шешімдерді функционалды интегралдар түрінде формальды жазуға болады. Қазіргі таңда бұл функционалды интегралдардың есептеу техникасы әлі жетілмеген жағдайда болып отыр, дегенмен бұл көріністі қажетті релятивистік түзетулерден тұратын потенциалы бар Фейнманның функционалды интегралы бейнесінде релятивистік емес Шредингер теңдеуінің шешімін алу үшін қолдануға болады.
Аталған бағытта әлі көп жұмыстар жасала қойған жоқ. Біздің жұмысымыз осы зерттеулерді жалғастырады.
Біздің жұмыста байланыс күйінің массасы қажетті кванттық сандары бар сәйкес токтардан корреляциялық функцияның асимптотикалық қалпы анықталады. Корреляциялық функция қажетті асимптотиканы бөліп алуға мүмкіндік беретін функционалды интеграл түрінде ұсынылады. [15] жұмыста ішкі калибрлық өрістегі зарядталған скаляр бөлшектер тогынан вакуумдық орташаны (Грин функциясын) асимптотикалық қалпын зерттеу негізінде энергетикалық спектрді есептеу тәсілі ұсынылған. Корреляциялық функцияның асимптотикалық қалпын анықтау кезінде функционалды интеграл бейнесіндегі көрініс пайдаланылады, сондықтан ішкі калибрлық өріс бойынша орташалау дұрыс орындалуы мүмкін. Алынған көрініс релятивистік емес кванттық механикадағы жол бойынша интегралданатын Фейнман функциясына [16] ұқсайды.
Осы кезде калибрлік өріс (фотон, глюон) алмасуы нәтижесінде пайда болатын әсерлесудің локалды емес функционалы (потенциал) Фейнман диаграммасымен анықталады және бөлшектердің меншікті энергиясына қалай үлес қосса, дәл солай байланыс күйінің құрылуына да үлес қосады. Олай болса, әсерлесу потенциалы Фейнман диаграмасының мүмкін болатын барлық типті үлестерімен мен анықталады.
Жұмыс мынандай сатылардан тұрады: бірінші бөлімде ішкі калибрлік өрістегі зарядталған бөлшектер тогының Грин функциясының асимптотикалық қалпы зерттеледі және байланыс күйінің массасын анықтайтын формула алынды. Әсерлесудің релятивистік табиғатымен байланысты әсерлесу гамильтонианына пертурбативті емес түзету аналитикалық жолмен анықталды; екінші бөлімде бұл тәсіл кулондық байланыс күйінің энергетикалық спектріне релятивистік түзетулерді есептеуге қолданылды; үшінші бөлімде глюонның массалық спектрі аналитикалық жолмен спин-спиндік, спин-орбиталдық әсерлесуді ескеріп анықталды және глюон байланыс күйінде массалы болатыны анықталды; төртінші бөлімде жеңіл- ауыр кварктерден тұратын мезондардың массалық спектрі орбиталдық және радиалдық қозулармен анықталды. Әсерлесудің модификацияланған потенциалы аналитикалық жолмен алынды. Алынған нәтижелер басқа ғалымдардың алған эксперименттік нәтижелерімен жақсы сәйкеседі. Соңында есептеулердің негізгі нәтижелері кесте арқылы көрсетілген. Қосымшада осциляторлық өрнектеу әдісі шеңберінде байланыс күйінің энергетикалық спектрін есептеу детальдары келтірілген.
I. РЕЛЯТИВИСТІК БАЙЛАНЫС КҮЙІНІҢ МАССАЛЫҚ СПЕКТРІН АНЫҚТАУ
1. 1 Релятивистік әсерлесу сипаттамасын ескере отырып байланыс күйдің массалық спектрін сипаттайтын үлгі
Біздің әдісті тереңірек қарастырайық.
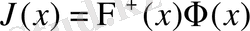 - скаляр зарядталған бөлшектердің тогы болсын. Аннигиляциялық каналды ескермейтін болсақ, онда қарастырып отырған корреляторымыз сыртқы калибірлік өрістегі
- скаляр зарядталған бөлшектердің тогы болсын. Аннигиляциялық каналды ескермейтін болсақ, онда қарастырып отырған корреляторымыз сыртқы калибірлік өрістегі
 скаляр бөлшектердің Грин функциясын
скаляр бөлшектердің Грин функциясын
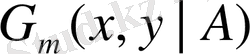 орташалау түрінде анықталады:
орташалау түрінде анықталады:
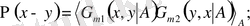 (1. 1)
(1. 1)
Сыртқы калибірлік өрістегі скаляр бөлшектерге арналған Грин функциясы
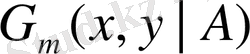 келесі теңдеуден анықталады:
келесі теңдеуден анықталады:
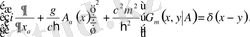 (1. 2)
(1. 2)
Бұл (1. 2) теңдеудің шешімін функционалды интеграл түрінде жазуға болады (есептің кейбір шығарылу жолдарын [17] -ден көріңіз) .
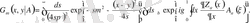 (1. 3)
(1. 3)
Мұнда мынандай белгілеулер енгізілді:
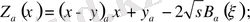
және интегралдау мөлшері
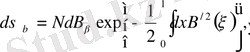 (1. 4)
(1. 4)
келесі нормалдау шартын қанағаттандырады:
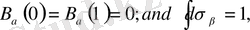 (1. 5)
(1. 5)
Мұндағы N - нормалау тұрақтысы. Сыртқы
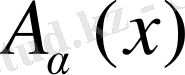 калибірлік өріс бойынша орташалағанда өріс формуласының төменгі дәрежелермен ғана шектелеміз, яғни тек екі нүктелі Гаусс корреляторын ғана ескереміз:
калибірлік өріс бойынша орташалағанда өріс формуласының төменгі дәрежелермен ғана шектелеміз, яғни тек екі нүктелі Гаусс корреляторын ғана ескереміз:
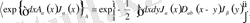 (1. 6)
(1. 6)
Мұндағы J α (x) -нақты ток, ал D αβ (x - y) - калибірлік өрістің пропагаторы, әдетте келесі теңдеуден анықталады:
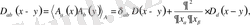 (1. 7)
(1. 7)
мұндағы
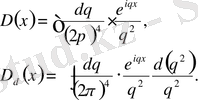 (1. 8)
(1. 8)
Осыларды ескерсек біздің тұзақ функциясының ролі Фейнман диаграмммасымен сипатталады.
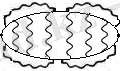
Сурет 1 - кварктерде глюон алмасу диаграммасы
Егер скаляр бөлшектерде көптеген глюон алмасу орындалса, 1-суретте көрсетілгендей сипатталады, бұны біз байланыс күй деп қарастыруымызға болады. Егер осы функция
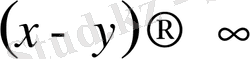 асимптотикалық шекке ұмтылса, онда келесі түрде жазылады:
асимптотикалық шекке ұмтылса, онда келесі түрде жазылады:
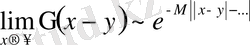 (1. 9)
(1. 9)
Байланысқан күйдің массасы шек сияқты анықталынады:
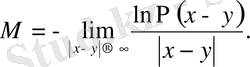 (1. 10)
(1. 10)
Бұл өрнектен көрініп тұрғандай, байланыс күйдің массасын
М
анықтау үшін
 асимтотикасындағы
асимтотикасындағы
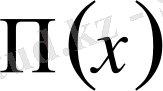 корреляциялық функцияны анықтау керек.
корреляциялық функцияны анықтау керек.
Грин функциясының орнына тұзақ функциясын қоя отырып және сыртқы калибірлік өріс бойынша орташаландыру жүргізе отырып, мына өрнекті аламыз:
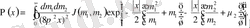 (1. 11)
(1. 11)
Бұл өрнектегі
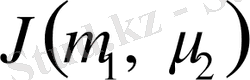 ток мынаған тең:
ток мынаған тең:
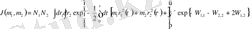 (1. 12)
(1. 12)
және келесі белгілеулер қолданылды:
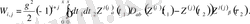 (1. 13)
(1. 13)
(1. 11) теңдеуі кванттық Грин функциясында
 локальді емес потенциал арқасында
локальді емес потенциал арқасында
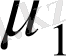 және
және
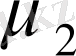 массалы екі бөлшек әсерлескен кездегі функционалды Фейнман интегралы түрінде мағынасы болады. Сондықтан
массалы екі бөлшек әсерлескен кездегі функционалды Фейнман интегралы түрінде мағынасы болады. Сондықтан
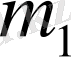 және
және
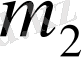 массалары токты, ал
массалары токты, ал
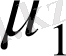 және
және
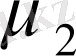 параметрлерін - конституенттік масса деп атайтын боламыз. (1. 11) теңдеуде функционалды интегралдау төрт өлшемді вектормен
параметрлерін - конституенттік масса деп атайтын боламыз. (1. 11) теңдеуде функционалды интегралдау төрт өлшемді вектормен
 және
және
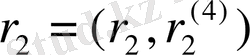 жүргізілетінін ескереміз. Сонымен қатар
жүргізілетінін ескереміз. Сонымен қатар
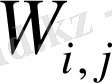 өлшемі мүмкін болатын Фейнман диаграммасы түрінің қосатын үлесімен анықталынады. Екі түрлі әсерлесу түрі бар: біріншісі калибірлік өріс әсерінен құраушы бөлшектердің әсерлесуі, оның қосатын үлесі
өлшемі мүмкін болатын Фейнман диаграммасы түрінің қосатын үлесімен анықталынады. Екі түрлі әсерлесу түрі бар: біріншісі калибірлік өріс әсерінен құраушы бөлшектердің әсерлесуі, оның қосатын үлесі
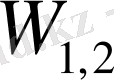 арқылы анықталынады, екіншісі - меншікті энергия диаграммасы болатын құраушы бөлшектердің бір бірімен әсерлесуі, оның қосатын үлесі
арқылы анықталынады, екіншісі - меншікті энергия диаграммасы болатын құраушы бөлшектердің бір бірімен әсерлесуі, оның қосатын үлесі
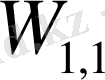 және
және
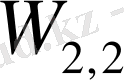 ретінде анықталынады. Релятивистік емес жағдайда
ретінде анықталынады. Релятивистік емес жағдайда
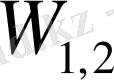 шамасы потенциалды әсерлесуге, ал
шамасы потенциалды әсерлесуге, ал
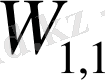 және
және
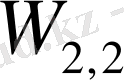 потенциалды емес әсерлесуге сәйкес келеді, потенциалды емес әсерлесулер бөлшек массасының қайта нормалауына қосқан үлесін анықтайды.
потенциалды емес әсерлесуге сәйкес келеді, потенциалды емес әсерлесулер бөлшек массасының қайта нормалауына қосқан үлесін анықтайды.
 асимптотикасында (1. 10) интегралы мына түрге келеді:
асимптотикасында (1. 10) интегралы мына түрге келеді:
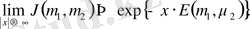 (1. 14)
(1. 14)
Мұндағы
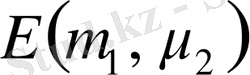 байланыс тұрақтысынан
байланыс тұрақтысынан
 және
және
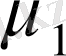 ,
,
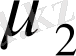 параметрлерінен тәуелді, ал m
1
және m
2
массаларынан тәуелсіз.
параметрлерінен тәуелді, ал m
1
және m
2
массаларынан тәуелсіз.
 кезде (1. 10) интегралы асу әдісімен есептелінеді. Байланысқан күйдің массасы асу нүктесімен анықталынады:
кезде (1. 10) интегралы асу әдісімен есептелінеді. Байланысқан күйдің массасы асу нүктесімен анықталынады:
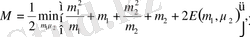 (1. 15)
(1. 15)
Сонымен барлық мәселе (1. 11) функционалды интегралды шешуге келіп тіреледі. Алайда бұл интеграл жалпы түрде шешілмейді және тек әртүрлі жуықтаулар шеңберінде ғана шешіледі. Қазіргі кезде нақты математикалық шығару үлгісі жоқ.
Сондықтан
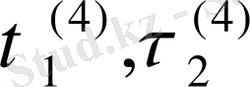 төртінші компенеттерімен интегралдауды орындауға жуықтау немесе әртүрлі физикалық болжамдарды енгізу керек. Мұндай интегералдау релятивистік емес шекке көшуге жақсы үйлеседі. Басқаша айтқанда, әсерлесудің локалды емес, релятивистік және пертурбативті емес қасиеттерімен байланысты әсерлесу потенциалы анықталады. Кейбір жағдайларда (1. 12)
төртінші компенеттерімен интегралдауды орындауға жуықтау немесе әртүрлі физикалық болжамдарды енгізу керек. Мұндай интегералдау релятивистік емес шекке көшуге жақсы үйлеседі. Басқаша айтқанда, әсерлесудің локалды емес, релятивистік және пертурбативті емес қасиеттерімен байланысты әсерлесу потенциалы анықталады. Кейбір жағдайларда (1. 12)
 -функциясындағы
-функциясындағы
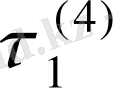 және
және
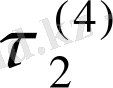 -ден тәуелділікті ескермесек, онда (1. 11) жүйе локалды потенциалы бар ЛЕКМ-ғы [16]
-ден тәуелділікті ескермесек, онда (1. 11) жүйе локалды потенциалы бар ЛЕКМ-ғы [16]
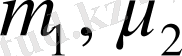 массалары бар скаляр бөлшектердің қозғалысына арналған траектория бойынша Фейнман интегралына келеді. Бұл жуықтауда (1. 10) -ға сәйкес
массалары бар скаляр бөлшектердің қозғалысына арналған траектория бойынша Фейнман интегралына келеді. Бұл жуықтауда (1. 10) -ға сәйкес
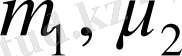 массалары бар скаляр бөлшектердің әсерлесу гамильтонианы мына түрде жазылады:
массалары бар скаляр бөлшектердің әсерлесу гамильтонианы мына түрде жазылады:
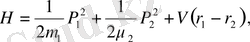 (1. 16)
(1. 16)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz