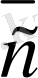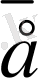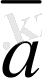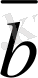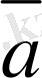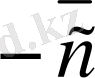Курстық жұмыс: Matlab-та векторлармен жұмыс және векторлық алгебра


Курстық жұмысты орындауға тапсырма
Студент: Нұрғазиев Берік Ермекұлы
Тақырыбы: Векторлармен жұмыс
Аяқталған жұмысты тапсыру уақыты:
«___»2005 ж.
Жұмыс барысында қолданылатын мәліметтер
Мазмұны
Жұмысты сипаттайтын негізгі бөлім
Қорытынды
Сызба материалдар саны: 0
Суреттер саны:
Кестелер саны:
Жұмыс жетекшісі: Умирбекова А. Н.
Тапсырманы орындауға қабылдап алған студент: Нұрғазиев Берік
«___»2005 ж.
Мазмұны
Кіріспе3
1 Matlab-та векторлармен жұмыс . . . . . . 5
1. 1 Векторларды Matlab -та енгізу . . . . . . 5
1. 2 Векторларды құру . . . . . . 5
1. 3 Векторларға матеметикалық және матеметикалық емес операциялар жасау . . . 6
1. 3. 1 Векторлық әрекет . . . . . . 7
1. 3. 2 Вектордың әрбір элементімен жұмыс. . ……8
2 Векторлық алгебра 11
2. 1. Вектор………. . . . 11
2. 2. Векторларды қосу . 12
2. 3. Векторлардың айырымы . . 14
2. 4 Векторларды санға көбейту . . . . 14
2. 5. Коллинеар және компланар векторлар . . …. . . . 15
2. 6. Базис . . . . . 16
2. 7. Кеңiстiктегi тiк бұрышты декарт координат жүйесiндегi вектордың проекциялары . . . 16
2. 8. Векторларға сызықты амалдар қолдану . . . 19
2. 9. Векторлардың коллинеар және компланар болу шарттары . . . . . 19
2. 10. Кесiндiнi берiлген қатынасқа бөлу. . . …. ………20
2. 11. Екi вектордың скаляр көбейтiндiсi және оның қасиеттерi . 21
2. 12. Координаттарымен берiлген екi вектордың көбейтiндiсi . …23
2. 13. Үш вектордың оң және терiс жүйесi . . . 23
2. 14. Екi вектордың векторлық көбейтiндiсi және қасиеттерi. . … . . . 24
2. 15. Координаттарымен берiлген екi вектордың векторлық көбейтiндiсi…26
2. 16. Параллелограмм және үшбұрыш аудандары . . . 26
2. 17. Үш вектордың аралас көбейтiндiсi және оның қасиеттерi. . . . . 27
3 Мысалдар . . . 29
Қорытынды . . . 34
Қолданылған әдебиеттер тізімі . . . 35
КІРІСПЕ
Matlab жүйесі (MATrix LABortory - Матрица лабораториясы) мәліметтер мапссивімен жұмысқа негізделген инженерлік және ғылыми есептеулерге арналған интерактивті жүйе. Matlab жүйесі дамыған математикалық және комплекстік арифметикадан тұрады.
Бұл жүйе векторлармен, матрицалармен және массивтермен операцияларды қолдайды, сингулярлы және спектралды айырылуды (разложение) іске асырады, матрица рангтарын есептейді, алгебралық полиномдармен, сызықтық емес теңдеулермен, дифференциалдық теңдеулермен және оптимизация есептерімен жұмыс жасайды, әртүрлі графиктермен тұрғызады.
1. Matlab-та векторлармен жұмыс
Matlab - векторлар, матрицалар және көпмүшелермен күрделі есептеулерге әдейі арналған жүйе.
Векторды бір өлшемді массив деп түсінеміз, ал матрицаны екі өлшемді массив деп түсінеміз. Matlab жүйесінде үнсіздік бойынша әрбір берілген айнымалы вектор не матрица ретінде қарастырылады. Мысалы, бөлек берілген кез келген санды программа (1*1) өлшемді матрица, ал N өлшемді(элементті) векторды (1*N) өлшемді матрица деп қабылдайды.
1. 1. Векторларды Matlab -та енгізу
Векторларды Matlab-та енгізу негізінен екі жолмен іске асырылады. Бірінші жолы - вектор атын, одан кейін “=” белгісі, сосын тік жақша ішіне үтір немесе бос орын арқылы бөліп жазу арқылы вектор элементтерін енгіземіз. Мысалы, v=[1 6. 7 99 -1. 8] жазсақ, онда бізге төмендегідей нәтиже береді.
>> v=[1 6. 7 99 -1. 8]
v =
1. 6. 7000 99. -1. 8000
Векторды енгізудің екінші жолы - вектордың элементтерін арифметикалық прогрессия өсуі немесе кемуі арқылы енгізу. Ол үшін вектор атын, одан кейін “=” белгісі, сосын вектордың алғашқы элементі, “:” белгісі, арифметикалық қадам, “:” белгісі, вектордың соңғы элементі енгізіледі. Мысалы, 2-мен 4 арасындағы қадамы 0. 5-ке тең элементтері бар х векторын құру.
>> x=2:0. 5:4
x =
2. 2. 5000 3. 3. 5000 4.
Matlab жүйесінде векторларды біріктіріп, бөлек вектор алуға болады. Мысалы, алдыңғы v және х векторларын біріктірейік. Нәтижесі төменде көрсетілген.
>> z=[v x]
z =
1. 6. 7000 99. -1. 8000 2. 2. 5000 3. 3. 5000 4.
1. 2. Векторларды құру
Векторларды құру үшін Matlab жүйесінің дайын функцияларын қолдануға болады. Негізінде Matlab жүйесі векторларға қарағанда матрицаларға дайын функциялары арналған және көп. Матрицаларға арналған функциялардың көбісі векторларға да жарайды. Қандайда бір функциядан вектор алатын болсақ, онда бір қатардан және N бағаннан тұратын матрица түрінде көрсетеміз.
zeros(1, N) - N нөлдік элементтен тұратын вектор құрады:
>> zeros(1, 6)
ans =
0 0 0 0 0 0
ones(1, N) - N бірлік элементтен тұратын вектор құрады:
>> ones(1, 6)
ans =
1 1 1 1 1 1
rand(1, N) - 0 мен 1 арасындағы кездейсоқ N элементтен тұратын вектор құрады:
>> rand(1, 6)
ans =
0. 9501 0. 2311 0. 6068 0. 4860 0. 8913 0. 7621
randn(1, N) - 0 мен 1 арасындағы нөлдік математикалық күтудің нормальды заңдылығымен үлестірілген және стандартты ауытқуы бірге тең кездейсоқ N элементтен тұратын вектор құрады:
>> randn(1, 6)
ans =
-0. 4326 -1. 6656 0. 1253 0. 2877 -1. 1465 1. 1909
fliplr(v) - v векторын вертикаль өске қарағанда орындарын ауыстырып құрады:
>> v=[5 9 3 4 8 7] ;
>> fliplr(v)
ans =
7 8 4 3 9 5
1. 3. Векторларға матеметикалық және матеметикалық емес
операциялар жасау
Matlab жүйесінде векторлармен жұмысты екі топқа бөлуге болады:
Векторлық әрекет - тек матеметикалық операциялар орындалады;
Вектордың әрбір элементімен жұмыс - мұнда вектордың әрбір элементіне керекті операция жасалады, бірақ векторлық алгебрада мұндай операциялар орындалмайды.
1. 3. 1. Векторлық әрекет
Векторларды қосу. Бұл операцияда вектордың әрбір сәйкес элементтерін қосады:
>> v=[5 6 9 8 7 3] ;
>> u=[6 5 3 1 9 4] ;
>> z=v+u
z =
11 11 12 9 16 7
Векторларды алу. Бұл да қосу сияқты сәйкес элементтерін бір-бірінен азайтады:
>> z=v-u
z =
-1 1 6 7 -2 -1
Транспонирлеу. Транспонирлеу транспонирлейтін вектордың шекесіне апостроф қою арқылы іске асырылады және нәтижесінде вектор-баған алынады:
>> z'
ans =
-1
1
6
7
-2
-1
Векторды санға көбейту. Векторды санға көбейту z=r*v немесе z=v*r формуласы жеткілікті. Мұнда v - берілген вектор, r - кез келген сан:
>> z=5*v
z =
25 30 45 40 35 15
Екі векторды көбейту. Екі векторды көбейту үшін екеуінің өлшемі бірдей және көбейткіш вектор - вектор-баған, көбейтілгіш вектор - вектор-қатар болу шарттары орындалса, онда нәтижесінде квадраттық матрица(диада) құрылады. Ал екі көбейткіштің орындары ауысса, онда нәтижесінде сан шығады:
>> u=[6 5 3 1 9 4] ;
>> v=[5 6 9 8 7 3] ;
>> z=u'*v
z =
30 36 54 48 42 18
25 30 45 40 35 15
15 18 27 24 21 9
5 6 9 8 7 3
45 54 81 72 63 27
20 24 36 32 28 12
>> z=u*v'
z =
170
Екі вектордың векторлық көбейтіндісі. Үш өлшемді екі векторды көбейтуге cross(v, u) функциясы арналған:
>> v=[3 7 4] ;
>> u=[2 6 9] ;
>> cross(v, u)
ans =
39 -19 4
1. 3. 2. Вектордың әрбір элементімен жұмыс
Вектордың әрбір элементімен жұмыста берілген вектордың әрбр элементін бөлек қарастырып, сол элементке операциялар жасалады. Matlab жүйесінде жазылу форматы былай болады: u=function(v), мұндағы v - берліген вектор, - функция аты, u - өлшемі v векторындай және әрбір элементтерінің мәндері v векторының сәйкес элементтерінен function функциясы бойынша өзгеріп отырады. Төменде бірнеше мысалдар келтірледі:
cos(v) - v векторының әрбір элементінің косинусын табады:
>> v=[-5 -2 0 1 4] ;
>> u=cos(v)
u =
0. 2837 -0. 4161 1. 0. 5403 -0. 6536
cot(v) - v векторының әрбір элементінің котангенсын табады:
>> cot(v)
Warning: Divide by zero.
> In C:\MATLAB6p1\toolbox\matlab\elfun\cot. m at line 8
ans =
0. 2958 0. 4577 Inf 0. 6421 0. 8637
log10(v) - v векторының әрбір элементінің ондық логарифмін табады:
>> v=[-10 -1 0 1 1000] ;
>> log10(v)
Warning: Log of zero.
> In C:\MATLAB6p1\toolbox\matlab\elfun\log10. m at line 13
ans =
1. + 1. 3644i 0 + 1. 3644i -Inf 0 3.
Matlab жүйесінде бұлардан басқа операциялар, атап айтқанда - мыналар(вектордың әрбір элементіне бір санды қосу не алу, екі векторды бөлу, дәрежеге шығару және т. б. ) :
>> v=[5 3 -4 0 9] ;
>> u=[3 -4 0 11 7] ;
>> v+4
ans =
9 7 0 4 13
>> u-6
ans =
-3 -10 -6 5 1
>> v. /u
Warning: Divide by zero.
ans =
1. 6667 -0. 7500 -Inf 0 1. 2857
>> v. \u
Warning: Divide by zero.
ans =
0. 6000 -1. 0 Inf 0. 7778
>> v. ^u
ans =
1. 0e+006 *
0. 0001 0. 0. 0 4. 7830
2 Векторлық алгебра
2. 1. Вектор
Mатематикада, физикада, механикада кез келген құбылыс екi шамамен анықталады. Егер кез келген шама оң немесе терiс санмен анықталса, онда ол скаляр шама деп аталады. Мысалы, көлем, масса, аудан, уақыт, температура - скаляр шама. Кейбiр шамаларды анықтау үшiн олардың сандық мәнiмен қоса, бағытын да бiлу қажет, олар - векторлық шама деп аталады. Мысалы үдеу, жылдамдық, күш - векторлық шама болып табылады.
Анықтама. Вектор дегенiмiз - бағытталған кесiндi.
Берiлген вектор үлкен екi латын әрiпiмен немесе кiшi бiр латын әрiптерiмен белгiленедi. Егер вектор екi әрiппен белгiленсе, онда бiрiншi әрiп вектордың
бастапқы нүктесi
, ал екiншiсi -
соңғы нүктесi
деп аталады. Мысалы
 - вектор, A нүктесi осы вектордың бастапқы нүктесi, ал B - соңғы нүктесi, стрелка
- вектор, A нүктесi осы вектордың бастапқы нүктесi, ал B - соңғы нүктесi, стрелка
 вектордың бағытын сипаттайды, яғни вектордың бағыты A нүктеден A нүктеге бағытталған (1-сурет) . Егер вектор кiшi бiр әрiппен белгiленсе, онда сол әрiптiң төбесiне тек сызықша ғана қойылады. Мысалы,
вектордың бағытын сипаттайды, яғни вектордың бағыты A нүктеден A нүктеге бағытталған (1-сурет) . Егер вектор кiшi бiр әрiппен белгiленсе, онда сол әрiптiң төбесiне тек сызықша ғана қойылады. Мысалы,
 векторын
векторын
 деп те белгiлеуге болады. Берiлген
деп те белгiлеуге болады. Берiлген
 векторының
үзындығы
немесе
модулi
деп, AB кесiндiсiнiң ұзындығын айтамыз және ол былай белгiленедi:
векторының
үзындығы
немесе
модулi
деп, AB кесiндiсiнiң ұзындығын айтамыз және ол былай белгiленедi:
 немесе
немесе
 .
.
E
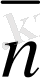
F
B
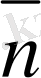
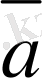 . 3
. 3
A
1-сурет
Модулдерi бiрге тең векторлар
бiрлiк
немесе
орт
векторлар
деп аталады. Берiлген
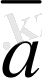 векторының орт векторы
векторының орт векторы
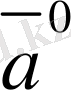 деп белгiленедi және оның бағыты
деп белгiленедi және оның бағыты
 векторының бағытымен бағыттас. Жалпы
векторының бағытымен бағыттас. Жалпы
 векторының орт векторын
векторының орт векторын
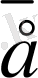 деп те белгiлейдi (2-сурет) .
деп те белгiлейдi (2-сурет) .
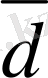
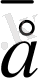
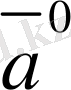
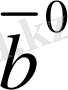
2-сурет
Аны қ тама. Екi вектор тең деп аталады, егер:
1. Oлар параллель болса (параллель түзулердiң бойында немесе бiр түзудiң бойында жатса) ;
2. Олардың бағыттары бағыттас болса;
3. Олардың модульдерi тең болса.
Екi
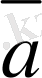 мен
мен
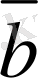 векторларының теңдiгiн былай белгiлеймiз:
векторларының теңдiгiн былай белгiлеймiз:
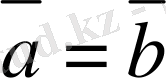 .
.
Анықтама. Егер екi вектор бiр түзудiң бойында немесе параллель түзулердiң бойында жатса, онда мұндай векторлар коллинеар векторлар деп аталады (3-сурет) .
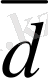
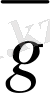
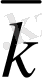
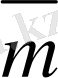
3-сурет
Егер вектордың бас нүктесiмен соңғы нүктесi бiр нүктеде үйлессе, онда мұндай вектор
нөл вектор
деп аталады да, былай белгiленедi:
 немесе
немесе
 ,
,
 . Нөл векторлардың бағыттары анықталмаған, модульдерi нөлге тең және олар өзара тең.
. Нөл векторлардың бағыттары анықталмаған, модульдерi нөлге тең және олар өзара тең.
 нөл векторы
нөл векторы
 нүктесiнен өтетiн кез келген түзулердiң бойында жатады, сондықтан нөл вектор - кез келген вектормен коллинеар деп айтуға болады. Кез келген вектор өзiне-өзi коллинеар бола алады.
нүктесiнен өтетiн кез келген түзулердiң бойында жатады, сондықтан нөл вектор - кез келген вектормен коллинеар деп айтуға болады. Кез келген вектор өзiне-өзi коллинеар бола алады.
Егер
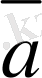 мен
мен
 векторлары параллель және модулдерi тең, ал бағыттары қарама-қарсы болса, онда мұндай векторлар
қарама-қарсы
векторлар
деп аталады (4-сурет) .
векторлары параллель және модулдерi тең, ал бағыттары қарама-қарсы болса, онда мұндай векторлар
қарама-қарсы
векторлар
деп аталады (4-сурет) .
4-сурет
Қарама-қарсы векторлардың байланысын былай көрсетемiз
 .
.
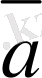 векторының қарама-қарсы векторын
векторының қарама-қарсы векторын
 деп белгiлеуге болады. Егер
деп белгiлеуге болады. Егер
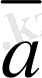 мен
мен
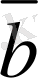 векторларының модулдерi ғана тең болса, онда бұл векторлардың өзара теңдiгi туралы ешқан-дай тұжырым айтуға болмай-ды, яғни олар жалпы жағдай-да тең немесе тең емес болуы да мүмкiн.
векторларының модулдерi ғана тең болса, онда бұл векторлардың өзара теңдiгi туралы ешқан-дай тұжырым айтуға болмай-ды, яғни олар жалпы жағдай-да тең немесе тең емес болуы да мүмкiн.
2. 2. Векторларды қосу
Берiлген
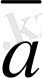 ,
,
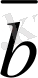 ,
,
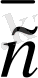 , . . . ,
, . . . ,
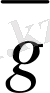 коллинеар емес векторларын былай орналастырайық:
коллинеар емес векторларын былай орналастырайық:
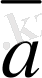 векторының соңғы нүктесi
векторының соңғы нүктесi
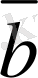 векторының бас нүктесiмен,
векторының бас нүктесiмен,
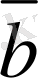 векторының соңғы нүктесi
векторының соңғы нүктесi
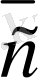 векторының бас нүктесiмен үйлестiрейiк, ал қалғандарында осылай тiзбектеп орналастырайық.
векторының бас нүктесiмен үйлестiрейiк, ал қалғандарында осылай тiзбектеп орналастырайық.
Анықтама.
Берiлген
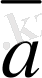 ,
,
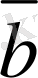 ,
,
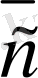 , . . . ,
, . . . ,
 векторларының
қосындысы
деп бас нүктесi
векторларының
қосындысы
деп бас нүктесi
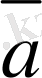 векторының бас нүктесiмен үйлесетiн, ал соңғы нүктесi
векторының бас нүктесiмен үйлесетiн, ал соңғы нүктесi
 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
 векторын айтамыз (5-сурет) .
векторын айтамыз (5-сурет) .
Осы векторлардың қосындысы былай белгiленедi:
+
+
+
+ . . . +
=
.
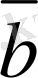
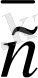
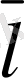
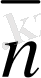
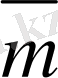
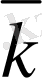
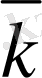
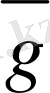
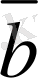
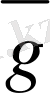
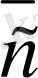
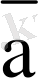
5-сурет
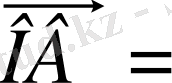
Жоғарыдағы анықтаманы пайдаланып, коллинеар емес
 мен
мен
 век-торларының қосындысын анықтайық. Ол үшiн
век-торларының қосындысын анықтайық. Ол үшiн
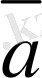 векторының соңғы нүкте-сiн
векторының соңғы нүкте-сiн
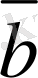 векторының бас нүктесiмен үйлестiрейiк, сонда
векторының бас нүктесiмен үйлестiрейiк, сонда
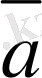 мен
мен
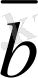 векторларының қосындысы
деп - бас нүктесi
векторларының қосындысы
деп - бас нүктесi
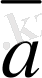 векторының бас нүктесiмен, ал соңғы нүктесi
векторының бас нүктесiмен, ал соңғы нүктесi
 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
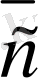 векторын айтады, яғни
векторын айтады, яғни
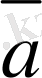 +
+
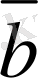 =
=
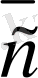 (6-сурет) .
(6-сурет) .
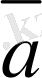 A
A
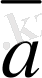 O
O
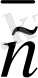
B
C
6-сурет
Берiлген
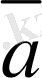 мен
мен
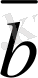 векторларының қосындысын табу үшiн
параллелограмм ережесiн
пайдаланып табуға да болады. Ол үшiн жа-зықтықтағы 0 нүктесiн берiлген
векторларының қосындысын табу үшiн
параллелограмм ережесiн
пайдаланып табуға да болады. Ол үшiн жа-зықтықтағы 0 нүктесiн берiлген
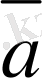 мен
мен
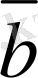 векторларының бас нүктесi етiп аламыз да, осы нүктеден
векторларының бас нүктесi етiп аламыз да, осы нүктеден
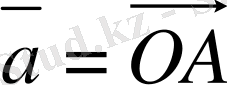 мен
мен
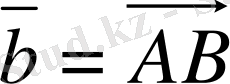 векторларын тұрғызамыз. Осы тұрғызылған векторлар арқылы
векторларын тұрғызамыз. Осы тұрғызылған векторлар арқылы
 параллелограмын саламыз. Параллелограмның
параллелограмын саламыз. Параллелограмның
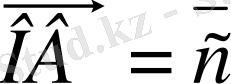 диагоналы, берiлген векторлардың қосындысы болады, яғни
диагоналы, берiлген векторлардың қосындысы болады, яғни
 +
+
 .
.
Жоғарыда берiлген анықтамадан, векторларды қосу амалына мына қасиеттер орындалады:
- - ауыстырымдылық заңы;
- - терiмдiлiк заңы;
- ;
- Кез келгенвекторына қарама-қарсывекторы табылып, теңдiгi орындалады.
2. 3. Векторлардың айырымы
Анықтама.
Берiлген
 мен
мен
 векторларының
айырымы
деп - үшiншi
векторларының
айырымы
деп - үшiншi
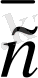 векторын айтамыз, егер
векторын айтамыз, егер
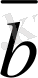 мен
мен
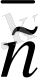 векторларының қосын-дысы
векторларының қосын-дысы
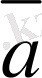 векторына тең болса
векторына тең болса
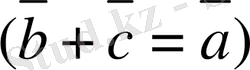 ол былай белгiленедi:
ол былай белгiленедi:
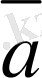 -
-
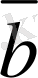 =
=
 .
.
Осы анықтаманы пайдаланып, берiлген
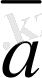 мен
мен
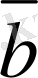 векторларының
векторларының
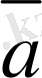 -
-
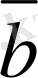 айырымын табайық. Ол үшiн
айырымын табайық. Ол үшiн
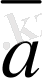 мен
мен
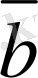 вектор-ларын ортақ бас О нүктесiмен үйлестiрелiк (7-сурет), яғни
вектор-ларын ортақ бас О нүктесiмен үйлестiрелiк (7-сурет), яғни
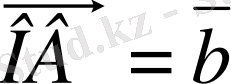 ,
,
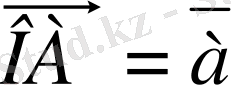 .
.
 -дан және жоғарыдағы анықтамадан мына теңдiктi аламыз:
-дан және жоғарыдағы анықтамадан мына теңдiктi аламыз:
 немесе
немесе
 .
.
Сонда,
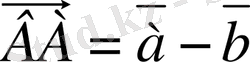 болады. Сонымен, берiлген
болады. Сонымен, берiлген
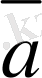 мен
мен
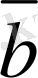 векторларының айырымын табу үшiн (7-сурет),
векторларының айырымын табу үшiн (7-сурет),
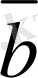
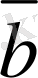
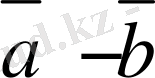
7-сурет
алдымен осы векторларды ортақ бас О нүктесiне үйлестiремiз де, бастапқы нүкте
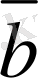 векторының соңғы нүктесiмен үйлесетiн, ал соңғы нүкте
векторының соңғы нүктесiмен үйлесетiн, ал соңғы нүкте
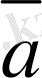 векторының соңғы нүктесiмен үйлесетiн
векторының соңғы нүктесiмен үйлесетiн
 векторын тұрғызамыз. Сонда, осы
векторын тұрғызамыз. Сонда, осы
 векторы
векторы
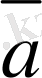 мен
мен
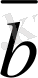 векторларының айырымы болады. Осы векторлардың айырымын қосу амалын пайдаланып та табуға болады. Ол үшiн
векторларының айырымы болады. Осы векторлардың айырымын қосу амалын пайдаланып та табуға болады. Ол үшiн
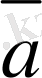 мен
мен
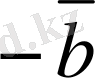 векторларының қосындысын анықтасақ жеткiлiктi,
векторларының қосындысын анықтасақ жеткiлiктi,
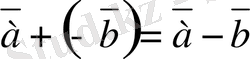 (8-сурет) .
(8-сурет) .
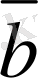
0
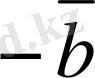
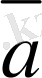
8-сурет
2. 1-теорема. Берiлген екi вектордың айырымы әрқашанда бар және ол тек бiреу ғана.
2. 4 Векторларды санға көбейту
Анықтама.
Берiлген
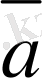 векторын скаляр
векторын скаляр
 санына көбейту
деп, мына үш шартты қанағаттандыратын
санына көбейту
деп, мына үш шартты қанағаттандыратын
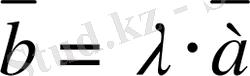 векторын айтамыз:
векторын айтамыз:
- ;
- . 3 мен. 3 векторлары коллинеар;
- Егер. 3 болса, онда. 3 мен. 3 векторларының бағыттары бiр бағыттас; егер. 3 болса, онда олардың бағыттары қарама-қарсы бағыттас.
Осы анықтамадан мынадай тұжырымдар аламыз:
егер
 немесе
немесе
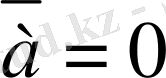 болса, онда
болса, онда
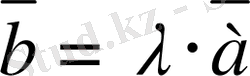 - нөл вектор;
- нөл вектор;
егер
 болса, онда
болса, онда
 . 3 мен
. 3 мен
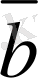 . 3 векторлары беттеседi;
. 3 векторлары беттеседi;
кез келген
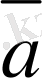 . 3 векторы үшiн
. 3 векторы үшiн
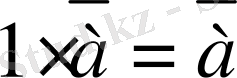 . 3 теңдiгi орындалады;
. 3 теңдiгi орындалады;
кез келген
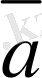 . 3 вектор мен
. 3 вектор мен
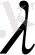 . 3 саны үшiн тек бiр ғана
. 3 саны үшiн тек бiр ғана
 векторы анықталады.
векторы анықталады.
Векторларды скаляр санға көбейту амалына мына қасиеттер орындалады (
 скаляр шама) :
скаляр шама) :
- ;
- ;
- .
2. 5. Коллинеар және компланар векторлар
2. 2-теорема.
Берiлген
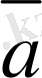 . 3 мен
. 3 мен
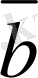 . 3 векторлары сызықты тәуелдi болу үшiн олардың өзара коллинеарлығы қажеттi, әрi жеткiлiктi.
. 3 векторлары сызықты тәуелдi болу үшiн олардың өзара коллинеарлығы қажеттi, әрi жеткiлiктi.
қажеттiлiгi.
Берiлген
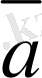 . 3 мен
. 3 мен
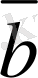 . 3 векторлары сызықты тәуелдi деп ұйғаралық та, олардың коллинеар екендiгiн дәлелдейiк. Ұйғаруымыз бойынша
. 3 векторлары сызықты тәуелдi деп ұйғаралық та, олардың коллинеар екендiгiн дәлелдейiк. Ұйғаруымыз бойынша
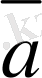 . 3 мен
. 3 мен
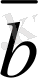 . 3 сызықты тәуелдi векторлар, сондықтан анықтама бойынша
. 3 сызықты тәуелдi векторлар, сондықтан анықтама бойынша
 . 3 мен
. 3 мен
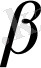 нақты сандары табылып,
нақты сандары табылып,
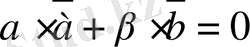 (2. 3)
(2. 3)
теңдiгi орындалады.
Ендi
 мен
мен
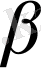 сандарының бiрiн, яғни
сандарының бiрiн, яғни
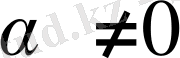 болсын дейiк, олай болса, (2. 3) теңдiктен мына теңдiктi аламыз:
болсын дейiк, олай болса, (2. 3) теңдiктен мына теңдiктi аламыз:
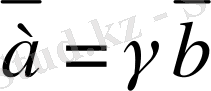 ,
,
мұндағы
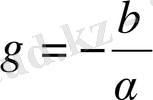 .
.
Соңғы теңдiктен және векторды скаляр санға көбейту анықтамасын еске түсiрсек, онда
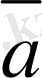 мен
мен
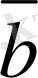 векторларының
коллинеар
екендiгi шығады.
векторларының
коллинеар
екендiгi шығады.
Жеткiлiктiлiгi.
Ендi
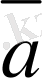 мен
мен
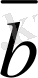 векторларын коллинеар деп үйғаралық та, олардың сызықты тәуелдi векторлар екендiгiн дәлелдейiк. Ол үшiн екi жағдайды қарастырамыз.
векторларын коллинеар деп үйғаралық та, олардың сызықты тәуелдi векторлар екендiгiн дәлелдейiк. Ол үшiн екi жағдайды қарастырамыз.
Бiрiншi жағдай. Берiлген векторлардың бiрi нөл вектор болсын делiк. Онда, бұл векторлардың сызықты тәуелдiлiгi бiрiншi қасиеттен алынады.
Екiншi жағдай.
Берiлген
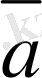 мен
мен
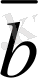 векторларының екеуi де нөл емес вектор делiк. Онда,
векторларының екеуi де нөл емес вектор делiк. Онда,
 . 3 нақты саны табылып, мына теңдiк орындалады:
. 3 нақты саны табылып, мына теңдiк орындалады:
 немесе
немесе
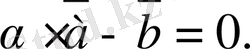 (2. 4)
(2. 4)
Соңғы теңдiкте, мынадай екi жағдай болуы мүмкiн
 . 3 немесе
. 3 немесе
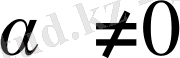 . 3. Екi жағдайда да
. 3. Екi жағдайда да
 болғандықтан, (2. 4) теңдiгi
болғандықтан, (2. 4) теңдiгi
 . 3 мен
. 3 мен
 . 3 векторларының сызықты тәуелдiлiгiн анықтайды. Теорема дәлелдендi.
. 3 векторларының сызықты тәуелдiлiгiн анықтайды. Теорема дәлелдендi.
Анықтама. Бiр жазықтықтың бойында жатқан немесе бiр жазықтыққа параллел болатын векторларды - компланар векторлар деймiз.
Осы анықтамадан, кез келген екi вектор - компланар болады.
2. 3-теорема.
Кез келген үш
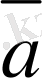 . 3,
. 3,
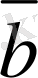 . 3,
. 3,
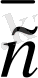 векторлар сызықты тәуелдi болу үшiн, олардың компланарлығы қажеттi, әрi жеткiлiктi.
векторлар сызықты тәуелдi болу үшiн, олардың компланарлығы қажеттi, әрi жеткiлiктi.
Осы теоремадан мынадай салдар аламыз.
Салдар.
Егер
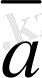 . 3,
. 3,
 . 3,
. 3,
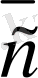 компланар емес векторлар болса, онда олар сызықты тәуелсiз.
компланар емес векторлар болса, онда олар сызықты тәуелсiз.
2. 6. Базис
Сызықтық және векторлық алгебрада базис ең негiзгi үғымдардың бiрi. Сондықтан бiз базис жайлы айтпақпыз.
Анықтама. Түзу бойындағы базис деп - осы түзу бойындағы кез келген нөл емес векторды айтамыз.
Анықтама. Жазықтықтағы базис деп - осы жазықтықтағы кез келген коллинеар емес екi векторды айтамыз.
Соңғы анықтама мен 2. 2-теоремадан: осы жазықтықта жатқан кез келген
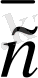 векторы үшiн
векторы үшiн
 мен
мен
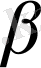 нақты сандары табылып,
нақты сандары табылып,
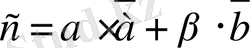 (2. 5)
(2. 5)
теңдiгi орындалады.
(2. 5) теңдiк,
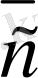 векторының
векторының
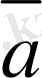 мен
мен
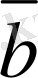 базистерi арқылы жiктелiнуi
деп аталады.
базистерi арқылы жiктелiнуi
деп аталады.
Анықтама.
Егер
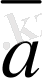 мен
мен
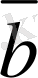 векторлары осы жазықтықтағы кез келген
векторлары осы жазықтықтағы кез келген
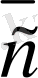 векторының сызықты комбинациясы болса, бiр жазықтықтағы сызықты тәуелсiз
векторының сызықты комбинациясы болса, бiр жазықтықтағы сызықты тәуелсiз
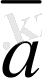 мен
мен
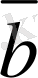 векторлары
бiр
базис құрайды
деймiз.
векторлары
бiр
базис құрайды
деймiз.
Анықтама.
Кеңiстiктегi сызықты тәуелiз
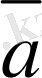 ,
,
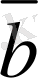 ,
,
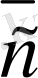 векторлары
бiр базис құрайды
деймiз. Егер олар кез келген
векторлары
бiр базис құрайды
деймiз. Егер олар кез келген
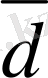 векторының сызықты комбинациясы болса, яғни кез келген
векторының сызықты комбинациясы болса, яғни кез келген
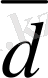 векторы үшiн
векторы үшiн
 ,
,
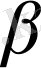 ,
,
 нақты сандары табылып,
нақты сандары табылып,
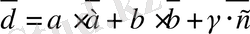 (2. 6)
(2. 6)
теңдiгi орындалады.
2. 4-теорема.
Кеңiстiкте компланар емес
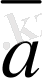 ,
,
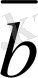 ,
,
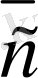 векторлары базис құрайды.
векторлары базис құрайды.
(2. 6) теңдiгiн
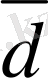 векторының
векторының
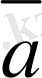 ,
,
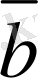 ,
,
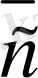 базистерi арқылы жiктелiнуi,
ал
базистерi арқылы жiктелiнуi,
ал
 ,
,
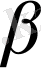 ,
,
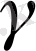 нақты сандар
нақты сандар
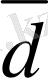 векторының осы базистерге тиiстi
координаттары
деп аталады.
векторының осы базистерге тиiстi
координаттары
деп аталады.
2. 5-теорема.
Кеңiстiктегi кез келген
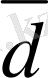 векторы
векторы
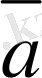 ,
,
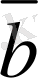 ,
,
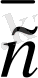 базистерi арқылы тек бiр-ақ рет жiктелiнедi, яғни (2. 6) теңдiк орындалады.
базистерi арқылы тек бiр-ақ рет жiктелiнедi, яғни (2. 6) теңдiк орындалады.
2. 7. Кеңiстiктегi тiк бұрышты декарт координат
жүйесiндегi вектордың проекциялары
Бiзге тiк бұрышты декарт координат жүйесi берiлсiн делiк. Координат өстерiндегi бiрлiк векторлар
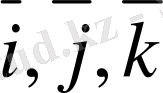 әрiптерiмен белгiленедi (9-сурет) . Координат жүйенiң бас
әрiптерiмен белгiленедi (9-сурет) . Координат жүйенiң бас
 нүктесi бiрлiк векторларының бас нүктесi болады. Кеңiстiкте жатқан кез келген
нүктесi бiрлiк векторларының бас нүктесi болады. Кеңiстiкте жатқан кез келген
 нүктенi алайық. Координат жүйенiң бас нүктесiнен шығып,
нүктенi алайық. Координат жүйенiң бас нүктесiнен шығып,
 нүктеге бақытталған вектор осы нүктенiң
радиус векторы
деп аталады да, былай белгiленедi:
нүктеге бақытталған вектор осы нүктенiң
радиус векторы
деп аталады да, былай белгiленедi:
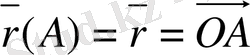 . Кеңiстiктегi кез келген нүкте үш санмен немесе үш координатпен анықталатыны бiзге белгiлi. Ендi берiлген координат жүйеге тиiстi
. Кеңiстiктегi кез келген нүкте үш санмен немесе үш координатпен анықталатыны бiзге белгiлi. Ендi берiлген координат жүйеге тиiстi
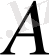 нүктесiнiң радиус векторының координаттарын анықтайық. Ол үшiн
нүктесiнiң радиус векторының координаттарын анықтайық. Ол үшiн
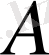 нүктеден координат жазықтықтарына параллель жазықтықтар тұрғызамыз. Осы жазықтықтардың координат жазықтықтарымен қиылысу нүктелерiн
нүктеден координат жазықтықтарына параллель жазықтықтар тұрғызамыз. Осы жазықтықтардың координат жазықтықтарымен қиылысу нүктелерiн
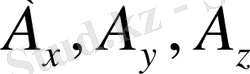 әрiптерiмен, ал
әрiптерiмен, ал
 нүктесiнiң координат жазықтықтарындағы проекцияларын
нүктесiнiң координат жазықтықтарындағы проекцияларын
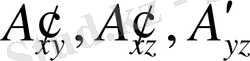 әрiптерiмен бел-гiлейiк. Ендi жазықтықтағы вектордың өстегi проекцияларының анықтамасын еске түсiрейiк. Бұл анықтамадан,
әрiптерiмен бел-гiлейiк. Ендi жазықтықтағы вектордың өстегi проекцияларының анықтамасын еске түсiрейiк. Бұл анықтамадан,
 нүктенiң координаттары
нүктенiң координаттары
 векторының координат өстерiне түсiрiлген проекциялар болып табылады, яғни
векторының координат өстерiне түсiрiлген проекциялар болып табылады, яғни
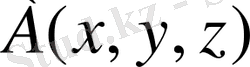 , ал
, ал
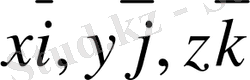 векторлары
векторлары
 векторының координат өстерiндегi
компоненттерi
деп аталады:
векторының координат өстерiндегi
компоненттерi
деп аталады:

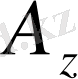
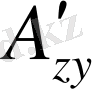
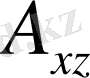
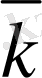
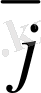
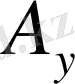
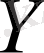
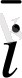
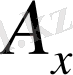
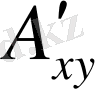
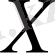
9-сурет
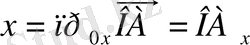 ,
,
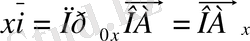 ,
,
,
, (2. 19)
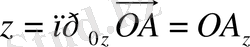 . 3,
. 3,
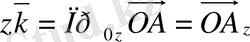 .
.
Сонымен, кеңiстiктегi кез келген
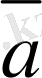 векторы тiк бұрышты координат жүйесiнде
векторы тiк бұрышты координат жүйесiнде
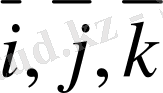 базистерi арқылы тек бiр-ақ рет жiктелiнедi, яғни
базистерi арқылы тек бiр-ақ рет жiктелiнедi, яғни
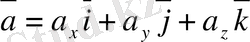 , (2. 20)
, (2. 20)
мұндағы
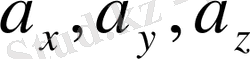 - нақты сандар,
- нақты сандар,
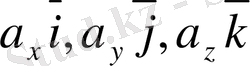 - вектордың компоненттерi.
- вектордың компоненттерi.
Анықтама.
Вектордың тiк бұрышты координат жүйесiндегi
координаттары
деп - осы вектордың координаттар өстерiндегi проекцияларын айтамыз, яғни (2. 20) формуладағы
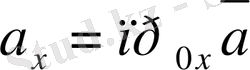 ,
,
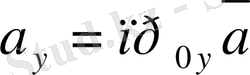 ,
,
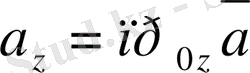 нақты сандары
нақты сандары
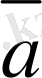 векторының координаттары болады және ол былай белгiленедi:
векторының координаттары болады және ол былай белгiленедi:
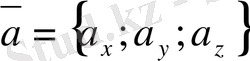 . (2. 21)
. (2. 21)
Егер вектордың бас нүктесi координат жүйесiнiң бас нүктесiмен үйлессе, онда ол вектордың координаттары осы нүктенiң координаттарына тең.
Ендi
 ,
,
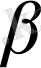 ,
,
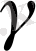 әрiптерi арқылы
әрiптерi арқылы
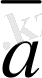 векторының координаттар өстерi арасындағы бұрыштарын белгiлейiк (10-сурет) . Осы бұрыштардың косинустары,
векторының координаттар өстерi арасындағы бұрыштарын белгiлейiк (10-сурет) . Осы бұрыштардың косинустары,
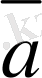 векторының
бағыттауыш косинустары
деп аталады.
векторының
бағыттауыш косинустары
деп аталады.

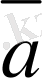

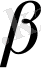 а
z
X
а
z
X

а y
Y а x
10-сурет
(2. 19) формуладан
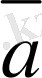 векторының координаттарын анықтаймыз:
векторының координаттарын анықтаймыз:
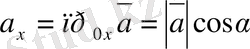 ,
,
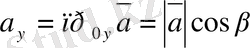 , (2. 22)
, (2. 22)
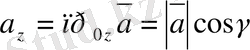 .
.
Тiк бұрышты параллелепипед диагоналының квадраты, оның үш өлшемiнiң квадраттарының қосындысына тең (9-сурет) :
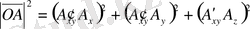
немесе
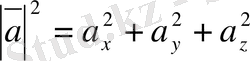 .
.
Сонымен,
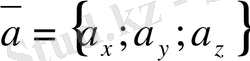 векторының модулiн мына формуладан анықтаймыз:
векторының модулiн мына формуладан анықтаймыз:
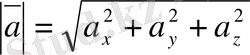 . (2. 23)
. (2. 23)
Ендi (2. 22) және (2. 23) формулаларынан, берiлген
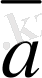 векторының бақыттауыш косинустарын анықтаймыз:
векторының бақыттауыш косинустарын анықтаймыз:
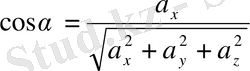 ,
,
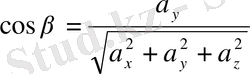 ,
,
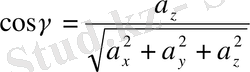 . (2. 24)
. (2. 24)
Соңғы формуладағы теңдiктердiң екi жағын квадраттап қосайық:
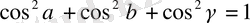 . (2. 25)
. (2. 25)
Сонымен, кез келген вектордың бағыттауыш косинус квадрат-тарының қосындысы бiрге тең.
Анықтама.
Берiлген
 векторының
орт (бiрлiк) векторы
деп, бағыты
векторының
орт (бiрлiк) векторы
деп, бағыты
 векторымен бағыттас және осы вектордың бойында жатқан бiрлiк векторды айтады, ол былай белгiленедi
векторымен бағыттас және осы вектордың бойында жатқан бiрлiк векторды айтады, ол былай белгiленедi
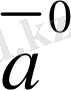 .
.
Осы анықтамадан және (2. 25) ôормóладан,
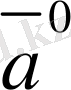 векторының координаттар өсi бойынша былай жiктелiнедi:
векторының координаттар өсi бойынша былай жiктелiнедi:
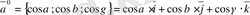 . (2. 26)
. (2. 26)
Егер
 векторының
векторының
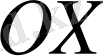 өсiндегi проекциясы нөлге тең болса, яғни
өсiндегi проекциясы нөлге тең болса, яғни
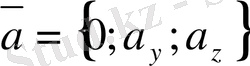 , онда
, онда
 векторы
векторы
 координат жазықтығына параллель болады. Осы сияқты
координат жазықтығына параллель болады. Осы сияқты
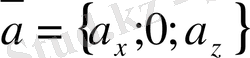 векторы
векторы
 жазық-тығына, ал
жазық-тығына, ал
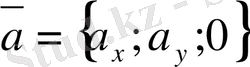 векторы
векторы
 жазықтығына да параллель.
жазықтығына да параллель.
Егер
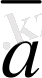 векторының
векторының
 пен
пен
 өстерiндегi проекциялары нөлге тең болса, яғни
өстерiндегi проекциялары нөлге тең болса, яғни
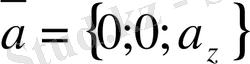 , онда
, онда
 векторы
векторы
 координат өсiне коллинеар болады. Осы сияқты
координат өсiне коллинеар болады. Осы сияқты
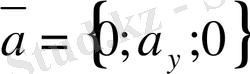 векторы
векторы
 өсiне, ал
өсiне, ал
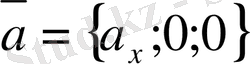 векторы
векторы
 өсiне коллинеар.
өсiне коллинеар.
2. 8. Векторларға сызықты амалдар қолдану
Векторларға сызықты амал қолдану нәтижесiнде жаңа вектор аламыз. Ендi осы жаңа вектордың координаттарын табу жолдарын қарастырайық. Ол үшiн бiзге екi вектор берiлсiн:
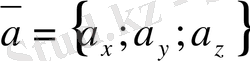 ,
,
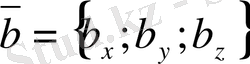 .
.
2. 6-теорема. Берiлген векторлардың қосындысын табу үшiн, олардың сәйкес координаттарын қосу керек, яғни
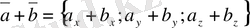 .
.
Осы теоремадан мынадай салдар аламыз.
Салдар.
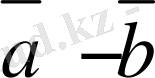 векторының координаттарын табу үшiн, бiрiншi вектордың координаттарынан, екiншi вектордың сәйкес координаттарын алу керек, яғни
векторының координаттарын табу үшiн, бiрiншi вектордың координаттарынан, екiншi вектордың сәйкес координаттарын алу керек, яғни
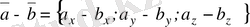 .
.
2. 7-теорема. Скаляр шаманы векторға көбейту үшiн, вектордың барлық координаттарын сол скаляр шамаға көбейту керек:
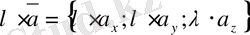 , мұндағы
, мұндағы
 - скаляр шама.
- скаляр шама.
Жоғарыдағы теоремалардан және вектор проекцияларының қасиеттерiнен, мына тұжырымдарды аламыз:
- Тең векторладың сәйкес координаттары тең;
- менвекторлары коллинеар.
2. 9. Векторлардың коллинеар және компланар болу шарттары
Бiзге
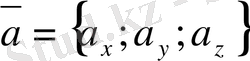 мен
мен
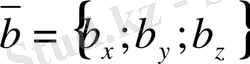 векторлары берiлсiн.
векторлары берiлсiн.
2. 8-теорема.
Нөл емес
 мен
мен
 векторлары коллинеар болу үшiн, олардың сәйкес координаттарының пропорционалдылығы қажеттi әрi жеткiлiктi, яғни:
векторлары коллинеар болу үшiн, олардың сәйкес координаттарының пропорционалдылығы қажеттi әрi жеткiлiктi, яғни:
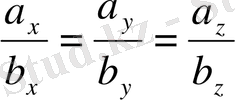 . (2. 27)
. (2. 27)
Осы теоремадан мынадай салдар аламыз.
Салдар.
Кеңiстiкте жатқан
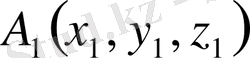 ,
,
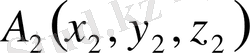 ,
,
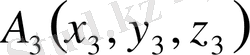 нүктелерi бiр түзудiң бойында жату үшiн
нүктелерi бiр түзудiң бойында жату үшiн
 мен
мен
 векторларының коллинеарлығы қажеттi әрi жеткiлiктi.
векторларының коллинеарлығы қажеттi әрi жеткiлiктi.
2. 9-теорема.
Берiлген
 ,
,
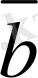 ,
,
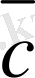 векторлары компланар болу үшiн, олардың координаттарынан анықталған үшiншi реттi анықтауыштың нөлге тең болуы қажеттi, әрi жеткiлiктi, яғни:
векторлары компланар болу үшiн, олардың координаттарынан анықталған үшiншi реттi анықтауыштың нөлге тең болуы қажеттi, әрi жеткiлiктi, яғни:
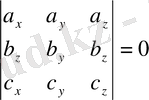 . (2. 28)
. (2. 28)
Осы теоремадан мынадай салдар аламыз.
Салдар.
Кеңiстiкте жатқан
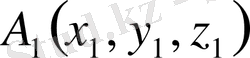 ,
,
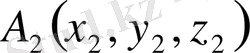 ,
,
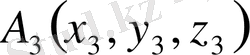 ,
,
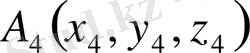 нүкте бiр жазықтықта жату үшiн
нүкте бiр жазықтықта жату үшiн
 ,
,
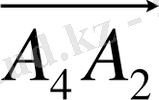 ,
,
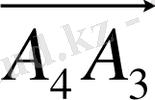 векторларының компланарлығы қажеттi әрi жеткiлiктi.
векторларының компланарлығы қажеттi әрi жеткiлiктi.
Сонымен, берiлген векторлар теореманың қажеттi әрi жеткiлiктi шартын , олар - компланар векторлар.
... жалғасы2. 10. Кесiндiнi берiлген қатынасқа бөлу
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz