Баротроптық қозғалыстағы тұтқырлы газ моделі үшін айырымдық сұлбанының орнықтылығы мен жинақтылығын зерттеу

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:

ӘЛ-ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ

МЕХАНИКА-МАТЕМАТИКА ФАКУЛЬТЕТІ

МАГИСТРАТУРА

Математикалық және компьютерлік пішіндеу кафедрасы

МАГИСТРЛІК ДИССЕРТАЦИЯ

Баротроптық қозғалыстағы тұтқырлы газ моделі үшін айырымдық сұлбанының орнықтылығы мен жинақтылығын зерттеу

Орындаушы Момынқұлова А. Қ. «___» 2014 ж.

/қолы/

Ғылыми жетекшісі

ф. -м. ғ. к., доцент Тұңғатаров Н. Н. «___» 2014 ж.

/қолы/

Кафедра меңгерушісінің

рұқсатымен

қорғауға жіберілді:

PhD, доцент Жакебаев Д. Б. «___» 2014 ж.

/қолы/

Алматы 2014

ТҮЙІНДЕМЕ

Диссертациялық жұмыс 60 беттен тұрады. Дисертацияда барлығы 44 әдебиет қолданылған.

Тәжірибеде туындайтын заманауи ғылым мен техниканың көптеген есептері газдық динамика теңдеуінің шешімімен байланысты. Осы теңдеулерді шешу үшін қазіргі таңда қолданылатын әдістердің көптігіне қарамастан оларды ары қарай зерттеу әлі күнге дейін өз маңыздылығы мен өзектілігін жоғалтпаған. Сол себепті, механика мәселелерін зерттеуде кездесетін есептер үлкен ғылыми және тәжірибелік қызығушылық тудырады. Себебі, олардың шешімі дифференциалдық теңдеулер және айырымдылық сұлба теориясының ары қарай дамуымен тікелей байланысты.

Жұмыстың мақсаты электр өрісін ескерген жағдайда, баротроптық қозғалыстағы тұтқырлы газ моделі үшін айырымдық сұлбаның орнықтылығы мен жинақтылығын зерттеу.

Жұмыс кіріспеден, негізгі бөлімнен, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

Бірінші бөлімде, дифференциалдық есептің қойылымы және негізгі нәтижелерін алынған.

Екінші бөлімде, (1. 9) - (1. 15) есебі үшін айырымдылық сұлбасын алынған.

Үшінші бөлімде, меншікті көлемнің айырымдылық аналогы үшін төменнен және жоғарыдан бағалауы алынған.

Төртінші бөлімде, жоғарғы ретті туындылардың бағалауы алынған.

Бесінші бөлімде, (2. 1) - (2. 5) айырымдылық сұлбасының жинақтылығы дәлелденген.

Алтыншы бөлімде, (2. 1) - (2. 5) айырымдылық сұлбасының орнықтылығы дәлелденген.

Жұмыстың барысында диссертация тақырыбына қатысты ғылыми еңбектерге шолу жасалады.

РЕЗЮМЕ

Диссертационная работа состоит из 60 страниц. В работе использованы 44 литературы.

Многие математические задачи современной науки и техники, возникающие на практике, связаны с решением уравнений газовой динамики. Несмотря на многочисленное количество методов, используемых в настоящее время для решения этих уравнений, работа по их дальнейшему изучению продолжает оставаться важной и актуальной. Поэтому задачи, встречающиеся при изучении проблем механики, представляют большой научный и практический интерес, поскольку их решение связано с дальнейшим развитием теории дифференциальных уравнений и разностных схем.

Цель работы заключается в исследовании на сходимость и устойчивость разностной схемы для модели баротропного движения вязкого газа в электрическом поле при наличии электрического поля.

Работа состоит из введения, основной части, заключения и списка использованной литературы.

В первой части говорится о постановке дифференциальных задач и основных результатах.

Во второй части приведены разностные схемы для задачи (1. 9) - (1. 15) .

Третья часть о получении оценках сверху и снизу для разностного аналога удельного обьема.

Четвертая часть о получении оценках на старшых производных.

В пятой части доказаны сходимость разностной схемы (2. 1) -(2. 5) .

В шестой части доказаны устойчивость разностной схемы (2. 1) - (2. 5) .

В начале работы проведен обзор известных научных трудов по теме диссертаций.

SUMMARY

The dissertation consists of 60 pages . We used the 44 literatures.

Many mathematical problems of modern science and technology arising in practice, related to the solution of equations of gas dynamics. In spite of numerous number of methods currently in use to solve these equations, work on their further study continues to remain important and relevant. Therefore, tasks occurring in the study of mechanics problems are of great scientific and practical interest because their decision is related to the further development of the theory of differential equations and difference schemes.

The aim of this work is to study the convergence and stability of difference schemes for the model of barotropic viscous gas in an electric field in the presence of an electric field.

The work consists of an introduction, body, conclusion and bibliography.

The first part said about differential formulation tasks and main results.

The second part are given difference scheme for the problem (1. 9) - (1. 15) .

The third part is about getting upper and lower estimates for the difference analogue of the specific volume.

The fourth part about getting estimates on higher derivatives.

In the fifth part we prove the convergence of the difference scheme (2. 1) - (2. 5) .

In the sixth part of the proven stability of the difference scheme (2. 1) - (2. 5) .

At the start of a review of known scientific papers on the topic of the thesis.

МАЗМҰНЫ

Нормативтік сілтемелер . . .

Нормативтік сілтемелер . . .: Шартты белгілер . . .

6: 7

Нормативтік сілтемелер . . .: Кіріспе . . .

6: 8

Нормативтік сілтемелер . . .: 1. Дифференциалдық есептің қойылымы және негізгі нәтижелер

6: 15

Нормативтік сілтемелер . . .: 2. (1. 9) - (1. 15) есебі үшін айырымдылық сұлбасы . . .

6: 17

Нормативтік сілтемелер . . .: 3. Меншікті көлемнің айырымдылық аналогы үшін төменнен және жоғарыдан бағалау . . .

6: 18

Нормативтік сілтемелер . . .: 4. Жоғарғы ретті туындыларды бағалау . . .

6: 34

Нормативтік сілтемелер . . .: 5. (2. 1) - (2. 5) айырымдылық сұлбасының жинақтылығы . . .

6: 45

Нормативтік сілтемелер . . .: 6. (2. 1) - (2. 5) айырымдылық сұлбасының орнықтылығы . . .

6: 53

Нормативтік сілтемелер . . .:

Қорытынды . . .

6: 57

Нормативтік сілтемелер . . .:

Пайдаланылған әдебиеттер тізімі . . .

6: 58

НОРМАТИВТІК СІЛТЕМЕЛЕР

Магистрлік диссертация Қазақстан Республикасы Ғылым жэне Білім Министрлігінің әл-Фараби атындағы Қазақ ұлттық университетінің келесідей нормативтік құжаттарына сүйене отырып жазылған:

Қазақстан Республикасының «Білім туралы» Заңы (№ 319 - III, 27. 07. 20 07) .
Қазақстан Республикасының «Білім туралы» Заңы.
«ҚР МЖМБС 5. 04. 033-2011. Жоғары оқу орнынан кейінгі білім. Магистратура».
«Магистрлік диссертацияға қойылатын талаптар» (әл-Фараби атындағы ҚазҰУ-дың Ғылыми Әдістемелік Кеңесінің Мәжілісінде 17. 02. 2012 ж. бекітілген (хаттама № 3) ) .

БЕЛГІЛЕУЛЕР МЕН ҚЫСҚАРТУЛАР

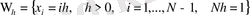− (0, 1) интервалындағы бірқалыпты кеңістіктік тор;

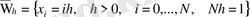− [0, 1] кесіндісіндегі бірқалыпты кеңістіктік тор;

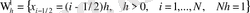− (0, 1) интервалындағы 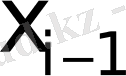және түйіндері арасындағы «жартылай тұтас нүктелердің» бірқалыпты кеңістіктік торы;

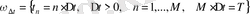− (0, T] -дағы бірқалыпты уақыттық тор;

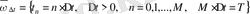− [0, T] кесіндісіндегі бірқалыпты уақыттық тор;

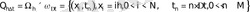, − тіктөртбұрыш облыстағы бірқалыпты тор;

− торның қадамы;

− [0, 1] кесіндісінің бөлікке бөлшектену саны;

− торының түйіндері;

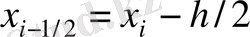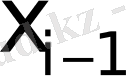− және түйіндері арасындағы «жартылай тұтас нүктелер»;

− уақыттық торының қадамы;

− [0, T] уақыттық кесіндісінің бөлікке бөлшектену саны;

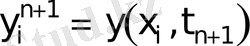− торындағы берілген функция;

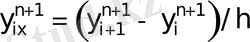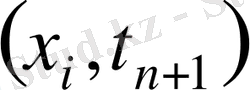− нүктесіндегі кеңістік бой

ынша оң жақ айырымдық туынды;

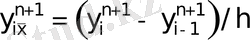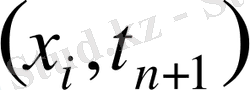− нүктесіндегі кеңістік бойынша сол жақ айырымдық туынды;

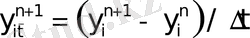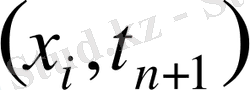− нүктесіндегі уақыт бойынша сол жақ айырымдық туынды;

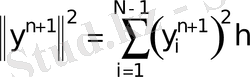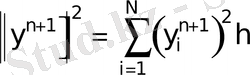, − кеңістігіндегі нормалардың торлық аналогтары.

КІРІСПЕ

«Электрогазодинамика» термині ең алғаш рет 1753 жылы Санкт-Петербург қаласында «Торжество Академии Наук» жинағында жарық көрген М. В. Ломоносовтың ғылыми жұмысының тақырыбында кездеседі. 1943 жылы М. Фарадей алғаш рет өзінің баяндамасында құбылыстың физикалық қағидасын келтірді, П. Армстронгтың гидроэлектрлік машинамен жүргізген тәжірибесін түсіндірді. бағыт бойынша орындалған жұмыстар: И. М. Кирко, Г. А. Остроумов, В. И. Попков, А. М. Мхитрарян, Е. И. Янтовский, В. А. Касьянов, Ю. М. Трушин, В. Е. Глазков, В. А Гогосов, И. Ф. Бабой, Е. П. Ударцев, Ю. С. Бортникова, И. Б. Рубашов, А. Б. Ватажин, В. И. Грабовский, В. А. Лихтер, В. И. Шульгин сияқты кеңес үкіметі ғалымдары мен О. Штуцер, М. Гурдин, М. Мельчер, Д. Тейлор, Н. Велкофф, Э. Барето, Н. Брандмайер, В. Кан, А. Маркс секілді шетел ғалымдарының еңбектері.

Электрогазодинамика (ЭГД) - электр өрісінде полярланған немесе униполярлы зарядталған сұйықтықтар мен газдардың қозғалысын зерттейтін физика мен механиканың бөлімі. ЭГД кейіннен құрылған бағыттардың бірі болып табылады. Күшті электр өрісінде газдың немесе полярланған, униполярлы зарядталған сұйықтардың қозғалысы барысында сол өрісте гидродинамикалық күштермен қатар өлшенетін шамалар реті бойынша электр күштері пайда болады. Бұл күштер гидродинамикалық ағынның қайта құрылуына әкеледі, соның салдарынан берілген электр өрісінің өзгеруіне әкеледі. Электрогазодинамика мен ЭГД-ның үдерістеріне деген қызығушылық жаңа дербес құрылғыларды (генераторларды, үдегіштерді, насостарды, дозаторларды және т. б. ) құрастыру мен зерттеу бойынша олардың практикалық қолданылу мүмкіндіктерімен жоғары деңгейде орнын табуда. Мұнда электр өткізгіштік орта электр өрісі бар құбыр немесе канал бойынша қозғалады.

үдерістердің техникалық қолданысының негізгі бағыттарына мыналар жатады: ЭГД - энергияның түрленуі, ЭГД - ортаның қасиеттерін басқару, ЭГД - технологиясы, ЭГД - диагностикасы, ЭГД - сепарациясы.

Энергияның түрленуімен байланысты ЭГД облысы мынандай екі бағытта дамиды: электр тоғын тудыратын ЭГД құрылғылар ( генератор) (М. Фарадей мен П. Армстронгтың жұмыстары) және электр өрісінің энергиясының механикалық энергияға (ионды-конвекциялы насос) түрленуін жүзеге асыратын ЭГД құрылғы. Аталмыш бағыт бойынша маңызды жұмыстарға Д. Авсеканың май мен ауадағы электроконвектті қозғалыстардың әртүрлі түрлері бойынша еңбектері мен В. И. Арабаджидің ауа мен электрошоғырланған сұйықтықта «электрлік желдің» гидродинамикасының экспериментті зерттеулері бойынша еңбектері жатады. 1953 жылы О. Штуцер ионды-конвекциялы насос идеясын ұсынды. «Маңызды желді» зерттеуге С. Аррениустың, А. Чаттоктың, А. Гюнтершульцтің, Х. З. Тайхманның еңбектері бағытталған. И. Ф. Бабойдың жұмысында ортаның физикалық параметрлерін басқару мәселесі ерекше сұрақтар шеңберін құрайды. Әсіресе тұтқырлық пен жылу алмасу үдерістерін басқаруға байланысты мәселелер ерекше назарды талап етеді.

Шеттік қабатты басқару мәселесі М. Гурдиннің, Э. Бареттоның, М. Ханның және Е. П. Ударцевтің жұмыстарында зерттелінген.

ЭГД - диагностикасы ортаның физикалық параметрлерін өлшеу мен анықтаудың негізгі заңдылықтарын пайдаланумен байланысты.

Ортаның электрлік өрісімен тікелей әсерінен туындайтын күш басқа да әрекеттегі күштермен салыстырмалы түрдегі шамасының реті бойынша арнайы математикалық және физикалық зерттеулерді қажет ететін сұйықтықтар мен газдардың ағындарын тривиал емес түрде құруға және басқа да эффектілердің туындауына әкеледі.

ЭГД - ағындарының жеке сұрақтарын толық зерттеу О. Штуцердің, Г. Копыловтың, В. А. Касьяновтың, М. Гурдиннің ЭГД - каналдардағы ағыны, ЭГД - ағысы, шеттік қабат мәселелерін сипаттау мен олардың тікелей физикалық зерттеулеріне (ағындардың диагностикасы, тасымалдау коэффициенттерін зерттеу) қатысты жұмыстарында қарастырылады.

ЭГД электрогазодинамика ағындарының пайда болу шарттарын зерттеу мен талдауына байланысты бірқалыпсыз зерттелінген. Аталмыш мәселенің жекеше сұрақтар, мысалы, электрфильтрдегі үдерістер толығымен қарастырылған, ал басқа сұрақтардың (мысалы, разряд) зерттеулері жалғасуда.

Конвективті электрохимияның жалпы есептері В. Г. Левич, Г. А. Остроумов, Р. Диксон және т. б. ғалымдардың атымен байланысты.

Өзектілігі. Тәжірибеде туындайтын заманауи ғылым мен техниканың көптеген есептері газдық динамика теңдеуінің шешімімен байланысты. Осы теңдеулерді шешу үшін қазіргі таңда қолданылатын әдістердің көптігіне қарамастан оларды ары қарай зерттеу әлі күнге дейін өз маңыздылығы мен өзектілігін жоғалтпаған. Сол себепті, механика мәселелерін зерттеуде кездесетін есептер үлкен ғылыми және тәжірибелік қызығушылық тудырады. Себебі, олардың шешімі дифференциалдық теңдеулер және айырымдылық сұлба теориясының ары қарай дамуымен тікелей байланысты. Олардың көмегімен газдық динамика теңдеулеріне келтірілетін механиканың, физиканың және техниканың көптеген есептері өз шешімдерін табуда. Мысалы, ұшу аппараттарының аэродинамикасы, астрофизика, ауа-райын болжау және т. б. Әсіресе практикада газодинамикалық ағындарға әртүрлі қосымша факторлардың, мысалы, электрлік, магниттік және гравитациялық өрістер, жылуөткізгіштік және электрөткізгіштік үдерістері, химиялық және басқа да үдерістердің әсер етуінен болатын есептер жиі кездесіп отырады. Осындай құбылыстарды ескерсе, есептердің математикалық дұрыс қойылуы мен шешілуі барысында көптеген қиындықтар мен проблемалар туындайды. Әдетте мұндай есептерді аналитикалық тәсілмен шешу теңдеудің күрделілігі мен сызықсыздығына байланысты жүзеге аса бермейді.

Тұтас орта қозғалысын сипаттайтын теңдеулердің шешімдерін анықтау туралы математикалық есебі уақыт пен үш кеңістікті айнымалылардан (мысалы, жылдамдық, көлем, қысым, температура, тығыздық, электрлік және магниттік кернеуі) белгісіз функцияларды іздеуге келтіріледі.

Бұл есеп көптеген жағдайларда өте күрделі болып табылады, және оны шешу үшін нақты физикалық есептердің қойылуына қатысты қосымша құрылуды енгізуді және олардың математикалық қойылымына мүмкін болатын қысқартуларды енгізуді қажет етеді.

Гидроаэродинамика модельдерінің арасында тұтқырлы сығылатын сұйықтықтың (тұтқырлы газ) Навье-Стокс теңдеулер жүйесінің орны ерекше . Себебі бұл модель сығылу мен жылуөткізгіштікке қоса, ортаның тұтқырлығын қарайды. Бұл жүйе өте күрделі, және ол аралас типтен тұрады, ал оған кіретін теңдеулер сызықты емес. Сол себепті, тұтқырлы газдың басқа да неғұрлым қарапайым модельдері пайдаланылады. Дербес жағдайда, егер баротроптық қозғалысы қарастырылса, онда энергия теңдеуі бөлінеді, алайда, мұндай жағдайда да жүйе өзінің негізгі ерекшеліктерін сақтап қалады, яғни сызықсыздық пен аралас типтілігін.

Тұтқырлы газдың қозғалысы есебін шешудің жалпы әдісі әлі кунге дейін табылмаған. Бұл Навье-Стокс теңдеуінің сызықсыздығымен түсіндіріледі. Сонымен қатар, сызықсыздық үлкен теориялық және практикалық қызығушылыққа ие эффектілерді туындайды.

Газдық динамика есептерін заманауи компьютерлердің көмегімен сандық шешу қазіргі таңда жалғыз тиімді әдіс болып отыр. Әртүрлі басқа шарттардың орындалуында зерттелінетін үдерістердің негізгі қасиеттерін неғұрлым айқын сипаттайтын болса және тордың неғұрлым жалпыланған кеңістіктік уақыттық есептелуінде қарастырылатын ағындардың жеткілікті дәл ерекшеліктерін ескерсе бұл әдіс анағұрлым тиімді әдіс болып табылады.

Математикалық физиканың сызықты теңдеулері үшін аппроксимация, орнықтылық және бұлардан туындайтын жинақтылық, осындай үш іргелі ұғымдарына сүйенетін айырымдылық сұлбалар теориясы жақсы дамыған.

Тегіс функциялар үшін айырымдылық сұлбасының аппроксимациясын зерттеу сызықты жағдай үшін де, сызықсыз жағдай үшінде ешқандай қиындықтар тудырмайды. Сұлбаның орнықтылығын дәлелдеу айырымдылық шешімінің есептің бастапқы берілуінен үзіліссіз тәуелділігін сипаттайтын кейбір априорлық бағаларын алуға келтіріледі. Сызықты жағдайға қарағанда мұндай бағаларды сызықсыз теңдеулер үшін құру үлкен қиындықтар туғызады /1/.

Газдық динамика есептеріндегі математикалық моделі үшін айырымдылық сұлбасын құру дифференциалдық және интегралдық теңдеулерімен сипатталатын үзіліссіз облыстың айырымдылық теңдеулер жүйесімен өрнектелетін облыстың қандайда бір дискретті аналогымен алмастыру ретінде қарастырылады. Бұған қоса, жаңа параметрлер пайда болады - кеңістік және айырымдылық тордың уақыты бойынша қадамдар. Практикада қолданылатын тордың ақырлы қадамдарында айырымдылық теңдеулерімен сипатталатын ортаның дискретті моделі айырымдылық шешімнің бағасын төмендететін үзіліссіз ортадан ерекшеленеді. Нақты есептеулерде қолданылатын күрделі, қадамдары үлкен торларда өзінің жақсы қасиеттерін сақтайтын өзгеше тор құру маңызды.

Газдық динамика теңдеуінің сандық интегралдануында, әдетте, айырымдылық сұлбасы мен ортаның нүктелерінің қатысты қозғалысымен, сонымен қатар, кеңістіктік туындыларды жуықтайтын айырымдылық теңдеулердің күрделілігімен ерекшеленетін лагранждық, эйлерлік және аралас эйлерлік-лагранждық әдістері қолданылады.

Лагранждық торлар ортаның бөлшектерімен бірге қозғалады және, сол себепті, оларды пайдаланытын әдістерде /2, 3-5/ конвективті тасымалға жауап беретін мүшелер болмайды. Контактылы үзілістердің және бос шеттердің қозғалуын есептеу және де жақсы таңдалған жасанды тұтқырлықта /6/ екпінді толқынды есептеу Лагранждық әдістердің басты ерекшелігі болып табылады.

Эйлер торлары қозғалмалы емес, сол себепті ол кеңістіктік туындының сандық жуықталуын ықшамдауға септігін тигізеді. Олар қарапайым және тиімді, күшті кеңістікті деформациялы ағындарды есептеуге мүмкіндік береді, алайда, масса диффузиясының жоғарғы жуықталуының бар болуынан контактылы үзілістерде ауытқулар, қателіктер пайда болады. Мұндай кемшілікті жеңуге әдетте ағындардың коррекция әдісі пайдаланылады.

Аралас эйлерлік-лагранждық әдістерінде нақты есептерге қатысты есептеулерді жүзеге асыруға мүмкіндік беретін қозғалмайтын координаттар жүйесіне де, ортаның бөлшектеріне қатысты алмастыратын айырымдылық сұлбалары пайдаланылады.

Эйлерлік, лагранждық немесе аралас эйлерлік-лагранждық айнымалылардың пайдалануына негізделген әдістерден басқа тұтас ортаны «бөлшек» немесе «бос нүктелер» түрінде өрнектеуіне негізделген алгоритмдердің кең классы бар. Кейінірек толығымен консервативтік сұлбалары құрылған болатын.

Айырымдылық сұлбаның консервативтілігі дегеніміз - испульстің және энергияның негізгі заңдарының сақталу. Толық консервативтілік үшін негізгі сақталу заңдарының айырымдылық аналогтарының орындалуынан басқа энергияның жекеше түрлерінің балансын, тепе-теңдігін тудыратын қосымша қатынастар қажет.

Айқын, толығымен консервативтік сұлбалар оңай шешілімді, бірақ аз дәрежеде орнықты. Әрине, орнықты айқын емес айырымдылық сұлбалар өлшемдері жоғары болатын сызықсыз алгебралық теңдеулер жүйесі болып табылады. Ал оларды шешу үшін тез жинақталатын итерациялық алгоритмдерді /7/ пайдалану қажет, мысалы, жинақтылықтың квадраттық жылдамдығы бар Ньютонның классикалық әдісі.

Г. А. Остроумовтың, Г. Н. Копыловтың, О. Штуцердің жұмыстары поляризациялық күштері жоқ сығылмайтын, термикалық біртекті орта жағдайларына арналған.

Қосымша шектеулері бар сығылатын сұйықтықтар үшін теңдеулер жүйесін зерттеу М. Гурдин мен Э. Бареттоның /1/, Ю. С. Бортников пен И. Б. Рубашовтің /8/, Y. Shohet /9/, Ю. Ф. Дейнега мен Г. В. Виноградовтың /10/. Виноградовтың жұмыстарында келтірілген, ал оларды талдау тұтқырлықсыз, диффузияның жылуөткізгіштігі мен поляризациялық күштерінсіз жүргізілген.

Термикалық және поляризациялық эффектілері жоқ электродинамикалық теңдеулердің жалпы жүйесі Р. Диксонның жұмыстарында, ал поляризациялық күштері бар электродинамикалық теңдеулер жүйесі Y. Shohet-тің жұмыстарында қарастырылған /9/.

Меншікті өткізгіштік ұғымындағы электродинамикалық теңдеулер жүйесі Г. А. Остроумов /11/ пен С. Смиттің /12/ еңбектерінде зерттелінген.

жалпы теңдеулері сызықсыз болып табылады және аралас типтегі жүйелерге кіреді. ЭГД теңдеулер жүйесі тұтқырлы сығылатын сұйықтықтың Навье-Стокс теңдеулер жүйесімен салыстырғанда анағұрлым күрделірек және олардың арасында кең ұқсастық бар, сонымен қатар, ЭГД есептерін шешуде газдық динамикада қолданылатын идеялар мен әдістерді пайдалануға болады. Сондықтан, тұтқырлы сығылатын газдың теңдеулері бойынша нәтижелерді ұсынамыз.

Жылуөткізгіш тұтқырлы газдың ағындарының математикалық зерттеу Дж. Серриннің жұмыстарынан бастау алады. Онда шекаралық есептердің негізгі қойылымы келтіріліп, тегіс шешімдер классында шешімнің жалғыздығы туралы теоремалары дәлелденген. Ал 1962 жылы Дж. Нэш сығылатын сұйықтықтың Навье-Стокс теңдеуі үшін шешімнің бар болуының бірінші теоремасын тұжырымдаған. Ол бастапқы берілген тегіс шамалар үшін Коши есебінің уақытқа тәуелді шешілімділігінің локальділігін дәлелдеді. Тура сондай нәтижелерді жапондық математик Н. Итая, сонымен қатар, А. И. Вольперт пен С. И. Худяев та келтірген болатын.

Жалпы алғанда, уақыт бойынша шешілімділікке қатысты сұрақтар Я. И. Канель /13-14/ зерттеп бастаған болатын. Ол жазық толқынды тұтқырлы газдың боротропты қозғалысы моделі үшін Коши есебін қарастырған болатын және де Коши есебінің глобальді қисындылығын дәлелдеген.

Жалпы уақыт бойынша тұтқырлы газдың теңдеуінің шешілімдлігі тек біртекті қозғалыс жағдайында ғана зерттелген. Н. Итая және Н. Тани /50/ Бюргерстің жалпыланған теңдеуі үшін алғашқы бастапқы-шекаралық есебі мен Коши есебін - тұтқырлы газдың изобаралық қозғалысы моделін қарастырған болатын.

Аралас бастапқы-шекаралық есептерді В. А. Солонников қарастырған болатын. Ол баротроптық қозғалыс жағдайында аз уақыт бойынша бар болу мен жалғыздық теоремасын дәлелдеген. Ал А. Тани - жылуөткізгіш тұтқырлы газ жағдайында дәлелдеген болатын. Жалпы уақыт бойынша Коши есебі мен аралас есептің шешімдерінің бар болуын А. Матсумура мен Т. Нишидо дәлелдеген.

Кейінірек А. В. Кажихов баротропты тұтқырлы газдық жүйесі үшін априорлық бағаларын алу әдісін ұсынған. Содан кейін ол вакуумдағы газдың қозғалысы есебінің қисындылығын дәлелдеген еді. Бүйір шекараларындағы біртектілік шарттарында бекітілген облыста жылуөткізгіш газдың қозғалысы үшін есептер жұмысында, ал біртексіздік шарттары жұмысында зерттелінген.

Біртекті жағдайында шекаралық есептердің «тұтас» шешілімділігі жұмыстарында зертелінген.

/15/ жұмысында В. В. Шелухин тұтқырлы сығылатын баротроптық газдың жылжымалы ағынын зерттеген, ал /16/-те Бюргерстің жалпыланған жүйесінің периодты шешімінің бар болуын көрсеткен. Екі өлшемді жағдай үшін шекаралық есептің глобальді шешілімділігін В. А. Вайгант пен А. В. Кажихов /17/ дәлелдеген.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.