Техникалық жүйелердің математикалық негіздері: тау-кен технологиясының статикалық және динамикалық модельдері мен модель алудың әдістері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 42 бет
Таңдаулыға:
Кіріспе
«Техникалық жүйелердің математикалық негіздерің пәнінен курстық жұмыс студенттердің осы пәннен алған білімдерін қорыту мен тереңдетуін мақсат етеді. Және де сол білімдерін автоматтандыру процесі мен өнеркәсіп құрылғыларын жекеше шешім табуда қолданады.
1 Өндіріс объектілерінің статикалық және динамикалық математикалық модельдерін анықтау
- Басқару объектілері және олардың математикалық моделдерінің түрлері
Технологиялық өндірісінің процестері, осы процестерге әсер ететін факторлар көп және олар әртүрлі. Басқару объектісі ретінде, өндіріс процестері анализінің күрделігін зерттеу кезінде белгілі бір иерархиялық құрылымды сақтау табиғи және қажетті болып табылады.
Арасында бағынушылық қатынас құрылатын үстеме, жүйе ретімен бөлшектенетін техникалық жүйе иерархиялық құрылымның негізі болып саналады.
Басқару мәселелері тарапынан тау-кен өндірісінің иерархиялық құрылымы үш сатыдан тұрады:
- Төменгі саты - тау-кен технологиясының типтік процестері (бұрғылау, жару, жеткізу, ұсақтау, ұнтақтау, сепарация, т. б. ) ;
- Ортаңғы саты - пайдалы қазба өңдіру және қайта өңдеудің технологиялық қызметтерін орындайтын аппарат немесе процестер тобы;
- Жоғарғы саты - жалпылай қаралатын шикізатты өңдіру және оның технологиялық желісі.
Өндіріс технологияның әрбір сатысы үшін өзінің бағытталған функциясына басқару міндеттері тән, олар әрбір объектінің қалыптасу процесін бейнелейтін математикалық модель түрін анықтайды. Жалпы жағдайда әрбір сатының математикалық моделін, тау-кен технологиясының күрделі объектісі ретінде қарастыруға және 3. 1-суретте келтірілген айнымалылардың кейбір функциялары ретінде ұсынуға болады. Мұнда объектінің кірісіне ықпалдың үш түрлі әсері бар:
1. Басқарылмайтын (бірақ бақыланатын) кіріс айнымалылары
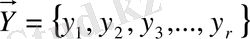 негізгі шикізаттың сапалы көрсеткіштерін сипаттайды, ауытқу векторы түрінде келеді.
негізгі шикізаттың сапалы көрсеткіштерін сипаттайды, ауытқу векторы түрінде келеді.
- Басқарылатын кіріс және материалдық ағымдардың сандық көрсеткішін сипаттайды, басқару векторы түрінде келеді.
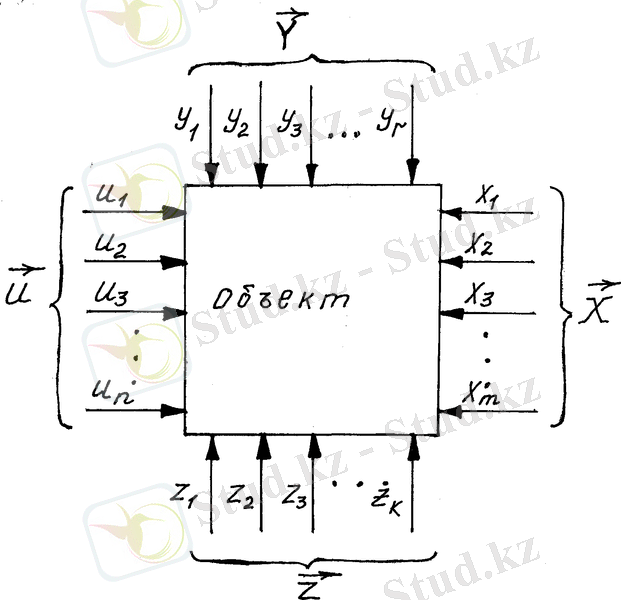
1. 1-сурет. Күрделі басқару объектінің құрылымы
- Бақыланбайтын факторларбөгеу векторы ретінде келеді. Бұл - мәні бойынша ауытқу векторы тәріздес. Бірақ, зерттеушілерде бұл туралы мәлімет өте аз немесе мүлдем белгісіз.
Кез келген технологиялық процестердің маңызы кіріс
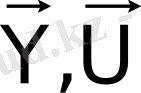 ықпалдарын, шығыстағы
ықпалдарын, шығыстағы
 -ке түрлендіруден тұрады.
-ке түрлендіруден тұрады.
 векторы - күй-жағдай векторы деп аталады және шығыстағы өнімнің сандық-сапалық белгісін сипаттайды.
векторы - күй-жағдай векторы деп аталады және шығыстағы өнімнің сандық-сапалық белгісін сипаттайды.
Тау-кен байыту технологиясының объектілерін, типтік процестерді бейнелейтін модельдер түрінде ұсынған ыңғайлы. Типтік операцияның төрт түрін бөліп қарастыруға болады:
- қарапайым;
- аралас;
- бөлінгіш;
- күрделі.
Бір кіріс У өнімнің шығыс Х өніміне қайта өңделуі - қарапайым операцияның ерекшелігі болып табылады. Бұл операцияны мына теңдеумен жазуға болады:
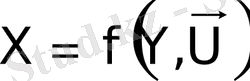 . (1. 1)
. (1. 1)
Мысалы, қарапайым операцияға кенді ұсақтау процесін жатқызуға болады. Себебі, мұнда ұсатқышқа келіп түсетін ірі-кесекті материалды тиеу ағыны - кірістегі айнымалыға жатады. Шығыстағы айнымалыға Х кесектер көлемімен бақыланатын ұсақталған материал; ал басқаруға әсер етушілерге - түсіру саңылауының ені
h
(мм)
, ұсатқыш кірісіндегі
Q
(
т/год)
ағынның өнімділігі, артудағы кесектердің ірілігі
d
(мм)
болып табылады, яғни
 .
.
Аралас операция -
бір шығыс
Х
ағынымен және объекті кірісіндегі
n
технологиялық ағынмен
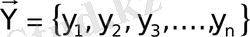 сипатталады. Осы операцияны мына теңдеумен жазуға болады:
сипатталады. Осы операцияны мына теңдеумен жазуға болады:
. (1. 2)
Бөлінгіш операция -
бір кіріс
Y
технологиялық ағынымен және шығыстағы
m
технологиялық ағынымен
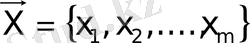 сипатталады. Бұл операцияны келесі теңдеумен жазуға болады:
сипатталады. Бұл операцияны келесі теңдеумен жазуға болады:
. (1. 3)
Мысалы, сеператор ұнтақталған кен ағыннын, ірілігі бойынша екі ағынға бөледі (дайын өнім
х
1
, айналынды жүктеме
х
2
) . Мұндағы басқарылатын ықпалға
Н
-жеңілдеткіштен туындайтын арын,
ϕ
-күрекшелердің қондырылу бұрышы, желдеткіш айналу
n
жиілігі жатады, яғни
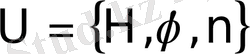 .
.
Күрделі операция - n
- кіріс технологиялық ағынымен және
 технологиялық ағынмен сипатталады (3. 1-суретт) . Күрделі операцияның басқарылуын мына теңдеумен келтіруге болады:
технологиялық ағынмен сипатталады (3. 1-суретт) . Күрделі операцияның басқарылуын мына теңдеумен келтіруге болады:
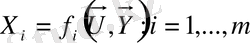 . (1. 4)
. (1. 4)
Әдетте күрделі - операция, құрамында бірнеше операциялардан түратын технологиялық схемаға сәйкес келеді. Мысалы: аралас және бөлінгіш операциялардың тізбектей қосылуы (шар тәріздес диірмен және классификатор) .
Тау-кен технологиясында типтік операциялар, олардың параллельді және тізбектелген қосылыстарынан құралады (1. 2-сурет) .
Агрегаттың қалыптанған жұмыс режимінде (1. 1-1. 4) тәуелділіктері, статикалық жұмыс режиміндегі математикалық модельдерін немесе объектілердің статикалық сипаттамаларын келтіреді (1. 3-сурет) .
Жалпы жағдайда, статикалық сипаттамалар - басқарылатын және басқарылмайтын
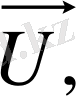
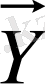 кіріс айнымалыларынан шығыс
кіріс айнымалыларынан шығыс
 айнымалылардың, сызықзыз түрде тәуелділігімен сипатталады.
айнымалылардың, сызықзыз түрде тәуелділігімен сипатталады.
.
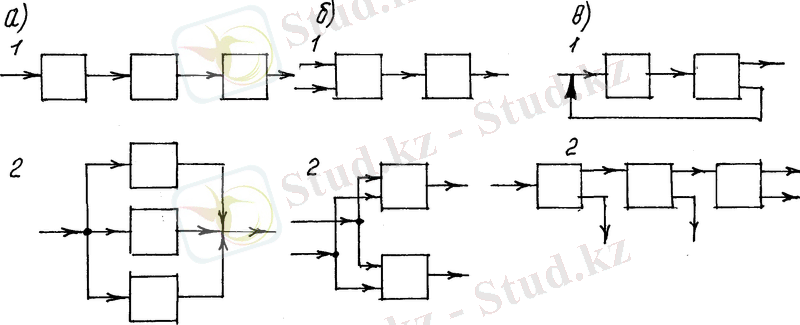
1. 2-сурет. Типтік операцияның түрлері
а - қарапайым операциялар (1 - тізбектей қосылған; 2 - паралель қосылған) ; ә - аралас операциялар (1 - қарапайым операциямен тізбектей қосылған; 2 - паралель қосылған) ; б- бөлінгіш операциялар (1 - рециклді схема; 2 - тізбектей қосылыс)
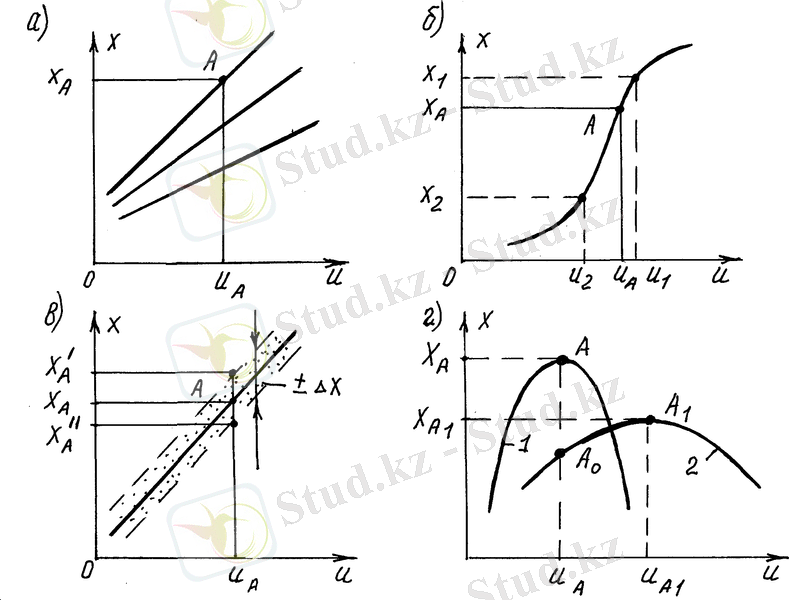
1. 3-сурет. Өнеркәсіптік объектілердің статикалық сипаттамалары
Тәжірибелік материал негізіне, статикалық сипаттамалар - дәрежелік көпмүше түрінде жиі ұсынылады:
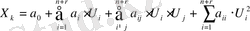 (1. 5)
(1. 5)
мұндағы а о - бос мүше; а і , а іj , а іі - шығыстағы Х к мәніне параметрлердің, олардың өзара әсері мен олардың квадраттарының әсер етуін сипаттайтын коэффициенттер.
(1. 5) теңдеуінде
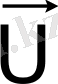 және
және
 кіріс айнымалылары бір әріппен, яғни
u
і
мен белгіленген (1. 1-сурет), сондықтан қосынды белгісінің жоғарғы шегі
n
және
кіріс айнымалылары бір әріппен, яғни
u
і
мен белгіленген (1. 1-сурет), сондықтан қосынды белгісінің жоғарғы шегі
n
және
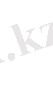 r индекстерінің қосындысы болады. Мысалы, екі басқару ықпалына
u
1
, u
2
(
n=2
) ие болатын қарапайым операцияның статикалық сипаттамасын былай суреттеуге болады:
r индекстерінің қосындысы болады. Мысалы, екі басқару ықпалына
u
1
, u
2
(
n=2
) ие болатын қарапайым операцияның статикалық сипаттамасын былай суреттеуге болады:
 . (1. 6)
. (1. 6)
(3. 4) теңдеуіне сәйкес бөлінгіш операцияда әрқашан статикалық сипаттамалау жүйесі орын алады. Мысалы,
 ,
,
 ,
,
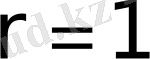 жағдайында:
жағдайында:
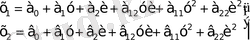
 (1. 7)
(1. 7)
Кей бір жағдайларда статикалық сипаттамалар сызықты болып келуі мүмкін. Онда (1. 5) теңдеуіндегі
 а
іj
және
а
іі
коэффициенттері нөлге тең болады. Бұл мына жағдайды көрсетеді, мысалы қарапайым операцияның (1. 6) статикалық сипаттамасы былай түрленеді:
а
іj
және
а
іі
коэффициенттері нөлге тең болады. Бұл мына жағдайды көрсетеді, мысалы қарапайым операцияның (1. 6) статикалық сипаттамасы былай түрленеді:
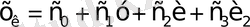 . (1. 8)
. (1. 8)
Сонымен қатар, жалпы жағдайда сызықтық емес статикалық (1. 6) мінездеменің
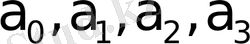 коэффициенттері
коэффициенттері
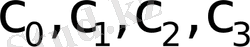 коэффициенттеріне тең емес.
коэффициенттеріне тең емес.
Статикалық сипаттамалар
. Автоматты басқару есептерінде статикалық сипаттамаларды, қондырғының жұмыс режимін анықтайтын
А
жұмыс нүктесін таңдау үшін қолданады. Осы құрылғының жұмыс режимінің тұрақтылығын, автоматты реттеу жүйесі жүзеге асырады. Сондықтан төңіректік сызықтық статикалық сипаттамалар, маңызды орын алады. Олар А таңдалған жұмыс нүктенің жақын маңында,
 шығыс көрсеткіштерінің басқаратын
шығыс көрсеткіштерінің басқаратын
 ықпалынан тәуелділігін белгілейді.
ықпалынан тәуелділігін белгілейді.
Практикада, техникалық себептерге байланысты, Y айнымалының шығыс Х шамасына әсерін, сандық түрде тура анықтау - өте көп жағдайларда мүмкін емес. Онда статикалық сипаттаманы тәуелдік түрінде көрсетуге болады:
Х = в о + в 1ƒ u. (1. 9)
бұл 1, 2, 3 сызықтарымен (1. 3 а -сурет) көрсетілгендей у- тің әртүрлі шамасы үшін берілген. у айнымалы жеткілікті нысан шекте өзгеріп, ал оның Х айнымалыға әсерін ескеру мүмкін болмаса, онда қарапайым операцияның статикалық Х=f(u) сипаттамасын мына түрде бейнелеуге болады:
Х
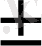
 Х = а
0
+ а
1ƒ
и
(1. 10)
Х = а
0
+ а
1ƒ
и
(1. 10)
мұндағы
 Х =
Х =
 - шығыс айнымалының сенімді аралығы (1. 3
в-
сурет) .
- шығыс айнымалының сенімді аралығы (1. 3
в-
сурет) .
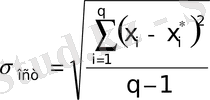
 - есептелген Х
і
*
мәнінен Х
і
дәл мәнінің қалдық орташа ауытқуы (ВС сызығы) ;
q
- мүшелердің экспериментальдық саны;
t
p
-
еркіндік дәрежесі
(q-1)
кезіндегі, берілген
- есептелген Х
і
*
мәнінен Х
і
дәл мәнінің қалдық орташа ауытқуы (ВС сызығы) ;
q
- мүшелердің экспериментальдық саны;
t
p
-
еркіндік дәрежесі
(q-1)
кезіндегі, берілген
 сенімді ықтималдық үшін алынған Стьюдент коэффициенті. Математикалық статистика курсынан (1. 10) өрнегіндегі
а
0
, а
1
коэффициенттерін,
сенімді ықтималдық үшін алынған Стьюдент коэффициенті. Математикалық статистика курсынан (1. 10) өрнегіндегі
а
0
, а
1
коэффициенттерін,
 Х
-ты есептеу әдісі белгілі.
Х
-ты есептеу әдісі белгілі.
Өнеркәсіптік объектілер әртүрлі статикалық сызықтық емес сипаттамалармен сипатталады. Бірқалыпты сызықтық емес сипаттамалардың кейбір түрлері, бірқатар ұйғарымдарды ескере отырып, сызықты тәуелділікпен ауыстырылуы мүмкін. Мысалы, А нүктесінің айналасында, и айнымалының и 1 - ден и 2 - ге дейін өзгеруі кезінде, (1. 3 ә - сурет) сызықтық емес тәуелділікті түзу сызықпен ауыстыруға болады. Бұл сызық А нүктесіндегі жанама түзу. Мүнда:
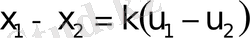 немесе
немесе
 . (1. 11)
. (1. 11)
Пропорционалдық
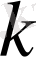 коэффицентін, А нүктесі үшін ғана әділетті болатын беріліс коэффициенті (күшейту коэффициенті) деп атайды.
коэффицентін, А нүктесі үшін ғана әділетті болатын беріліс коэффициенті (күшейту коэффициенті) деп атайды.
Жұмыс нүктесі статикалық сипаттаманың бойымен жылжыса (технологиялық агрегаттың жұмыс тәртібі өзгерсе),
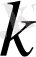 коэффициентінің мәні де өзгереді.
коэффициентінің мәні де өзгереді.
Егер объектінің статикалық сипаттамасы аналитикалық түрде берілсе, онда А нүктесінің айнымалысындағы сызықтандыру,
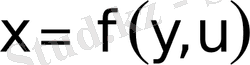 тәуелділігін, нүктенің айналасында Тейлор қатарына жіктеу және де екінші мен жоғарғы дәрежелі мүшелерді есепке алмау.
тәуелділігін, нүктенің айналасында Тейлор қатарына жіктеу және де екінші мен жоғарғы дәрежелі мүшелерді есепке алмау.
Статикалық сипаттамалардың кейбір түрлері сызықтандырылмайды. 1. 3
г
-суретінде кіріс айнымалының
y
әртүрлі мәндері кезіндегі (1 және 2 қысық) экстремальды статикалық сипаттамалар келтірілген. Көрсетілген түрлі сипаттамалар бірқатар обьектілер үшін (бұрғылау, ұсақтау процестері) әдетті болып келеді. А жұмыс нүктесі
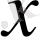 шығыс айнымалысының экстремалды мәнінің аумағында болса, мұндай құрылғыларда тәртіптің тиімдісі болып -
y
кіріс айнымалысы өзгерсе, онда
х0и
жазықтығында,
шығыс айнымалысының экстремалды мәнінің аумағында болса, мұндай құрылғыларда тәртіптің тиімдісі болып -
y
кіріс айнымалысы өзгерсе, онда
х0и
жазықтығында,
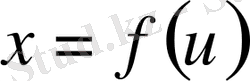
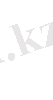 статикалық сипаттамасы да,
статикалық сипаттамасы да,
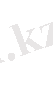 жылжиды (1. 3
в-
сурет) .
y
1
мәнінде жұмыс нүктесі, 1-ші статикалық сипаттаманың А нүктесінде болса, онда
y
2
мәнінде,
жылжиды (1. 3
в-
сурет) .
y
1
мәнінде жұмыс нүктесі, 1-ші статикалық сипаттаманың А нүктесінде болса, онда
y
2
мәнінде,
 статикалық сипаттама 2-ші күйге ауысады. Бұл жағдайда, басқару ықпалы
статикалық сипаттама 2-ші күйге ауысады. Бұл жағдайда, басқару ықпалы
 болса, жұмыс нүктесі
болса, жұмыс нүктесі
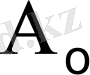 күйінде болады. 2-ші қисықтың экстремулына сәйкес келетін
күйінде болады. 2-ші қисықтың экстремулына сәйкес келетін
 нүктесіне,
нүктесіне,
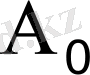 жұмыс нүктесінің ауыстырылуы, экстремальды басқарудың қызметі болады. Бұл жағдайда,
и
басқару ықпалы
жұмыс нүктесінің ауыстырылуы, экстремальды басқарудың қызметі болады. Бұл жағдайда,
и
басқару ықпалы
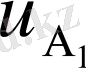 шамасына сәйкес келу керек.
шамасына сәйкес келу керек.
Бақыланбайтын
Z
ықпалының үздіксіз өзгеруі кезінде (1. 3
в
-сурет), 1-қисығы ақырындап ығысады. Бұл дегеніміз -
 теңдеуіндегі
а
0
, а
1
, а
2
коэффиценттері уақыт аралығында өзгеруі. Ал экспериментальды статикалық сипаттаманың теңдеуі төмендегідей:
теңдеуіндегі
а
0
, а
1
, а
2
коэффиценттері уақыт аралығында өзгеруі. Ал экспериментальды статикалық сипаттаманың теңдеуі төмендегідей:
х= а 0 (t) + а 1 (t) Һи + а 2 (t) Һи 2 . (1. 12)
Математикалық модельдері, уақыт функциясындағы а і - коэффициенттерінен тұратын, технологиялық объектілерді стационарлы емес объект деп атайды. Станционарлы емес жағдайлар, сонымен бірге тұрақты тозуда, деформацияда, технологиялық элементтердің кейбір элементтерінің қасиеттері өзгеруінде байқалады.
Кейбір жағдайларда, статикалық сипаттамаларды нақты түрде келтіру, яғни шығыстағы
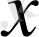 айнымалысын салыстырмалы түрде шешу мүмкін емес, онда олар нақты болмайды. Мысалы, қарапайым операцияның статикалық сипаттамасы ретінде:
айнымалысын салыстырмалы түрде шешу мүмкін емес, онда олар нақты болмайды. Мысалы, қарапайым операцияның статикалық сипаттамасы ретінде:
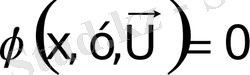 . (1. 13)
. (1. 13)
Динамикалық сипаттамалар
. Статикалық сипаттамада объектінің басқарылатын кіріс
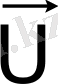 айнымалысының әсерімен,
а
нүктесінен
б
жұмыс нүктесі орын ауыстырады (1. 4
а
-сурет) .
б
нүктесінде объектінің жаңа қалыптасқан жұмыс тәртібі орнатылуы мүмкүн. Кірістегі әсердің сатылы түрде өзгеруінде, мысалы
айнымалысының әсерімен,
а
нүктесінен
б
жұмыс нүктесі орын ауыстырады (1. 4
а
-сурет) .
б
нүктесінде объектінің жаңа қалыптасқан жұмыс тәртібі орнатылуы мүмкүн. Кірістегі әсердің сатылы түрде өзгеруінде, мысалы
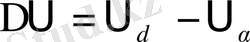 шамасына,
шамасына,
 уақыты кезінде (1. 4
ә
-сурет), шығыс
уақыты кезінде (1. 4
ә
-сурет), шығыс
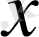 шамасы қалыптасқан
х
б
мәніне (97%-ке) жедел емес, ал
шамасы қалыптасқан
х
б
мәніне (97%-ке) жедел емес, ал
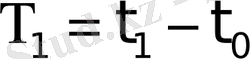 уақытында жетеді (1. 4
б
-сурет) . Бұл уақыт - ауыспалы процесс уақыты болып табылады, яғни
X(t)
айнымалысының нөлден (1 нүктесінде)
уақытында жетеді (1. 4
б
-сурет) . Бұл уақыт - ауыспалы процесс уақыты болып табылады, яғни
X(t)
айнымалысының нөлден (1 нүктесінде)
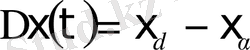 (2-нүктесіне) мәніне дейін өзгеруі.
(2-нүктесіне) мәніне дейін өзгеруі.
 - объектінің динамикалық қасиетін көрсетеді. Егер
- объектінің динамикалық қасиетін көрсетеді. Егер

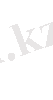 болса, онда объект инерциясыз деп саналады және керісінше, ауыспалы процестің
болса, онда объект инерциясыз деп саналады және керісінше, ауыспалы процестің
 уақыты көп болған сайын, объект инерциялы болады.
уақыты көп болған сайын, объект инерциялы болады.
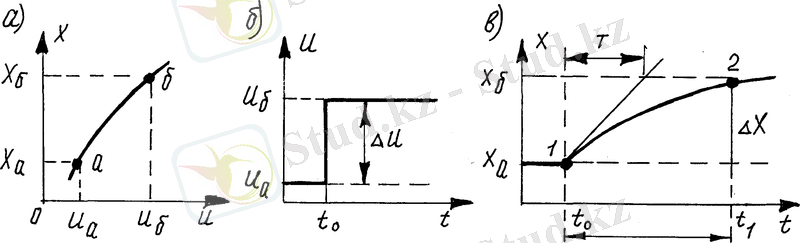
1. 4 - сурет. Сатылы кіріс (ә) ықпалы кезіндегі объектілердің статикалық және динамикалық сипаттамалары.
Бірінші жуықтауда, объект кірісіне сатылы түрдегі
 басқару ықпал берілген кезде,
басқару ықпал берілген кезде,
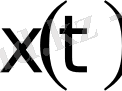 айнымалының статикалық сипаттамасы
а
нүктесінен
ә
нүктесіне дейінгі интервалдағы өзгерісін, бірінші ретті инерциалдық буынның дифференциалды теңдеуі түрінде жазуға болады:
айнымалының статикалық сипаттамасы
а
нүктесінен
ә
нүктесіне дейінгі интервалдағы өзгерісін, бірінші ретті инерциалдық буынның дифференциалды теңдеуі түрінде жазуға болады:
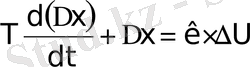 (1. 14)
(1. 14)
мұндағы
Т
-
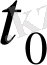 моментінен,
X
айнымалының жаңа қалыптасқан 3 сызығымен 1-3 жанаманың (1. 4
б
-сурет) қиылысқан 3 нүктесіне дейінгі уақыт бөлігіне тең, уақыт тұрақтылығы,
с
:
моментінен,
X
айнымалының жаңа қалыптасқан 3 сызығымен 1-3 жанаманың (1. 4
б
-сурет) қиылысқан 3 нүктесіне дейінгі уақыт бөлігіне тең, уақыт тұрақтылығы,
с
:
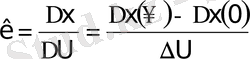
- беріліс коэффициенті.
Объектінің қалыптасқан жұмыс тәртібіндегі (
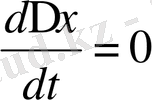 болса) (1. 14) өрнегі,
а
нүктесінен
б
нүктесіне дейінгі интервалдағы (1. 4
а
-сурет) сызықтандырылған
болса) (1. 14) өрнегі,
а
нүктесінен
б
нүктесіне дейінгі интервалдағы (1. 4
а
-сурет) сызықтандырылған
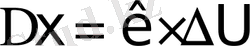 статикалық сипаттамасына түрленеді.
статикалық сипаттамасына түрленеді.
(1. 14) дифференциалды теңдеуін нормальдық формада ұсынуға болады (Коши формасы) :
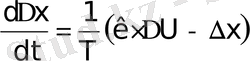 . (1. 15)
. (1. 15)
Жалпы жағдайда, уақыт тұрақтылығы объектінің затты немесе энергияны жинау және тарату қабілеттілігін сипаттайды.
Объектінің инерциялық қасиетін сипаттайтын басқа бір параметрге таза немесе транспорттық кешігу
 жатады. 1. 5
а, ә, б
-суретінде транспорттық кешігуі бар және кірісіне сатылы ықпал берілген кездегі (1. 5
в-
сурет) технологиялық объектілердің ауыспалы функцияларының типтері көрсетілген. Мұнда айнымалылар салыстырмалы түрде ұсынылған, яғни:
жатады. 1. 5
а, ә, б
-суретінде транспорттық кешігуі бар және кірісіне сатылы ықпал берілген кездегі (1. 5
в-
сурет) технологиялық объектілердің ауыспалы функцияларының типтері көрсетілген. Мұнда айнымалылар салыстырмалы түрде ұсынылған, яғни:
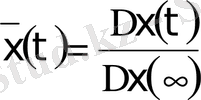 және
және
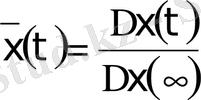 .
.
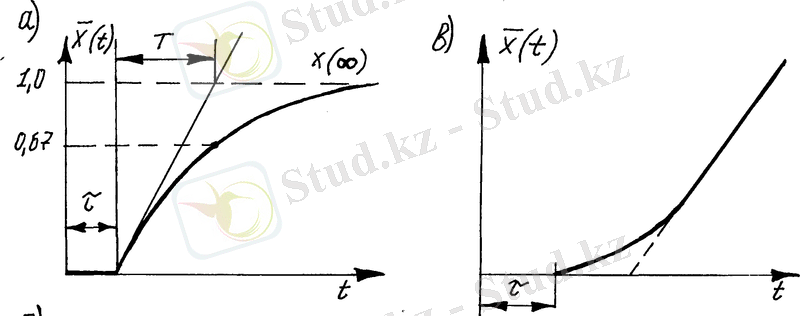
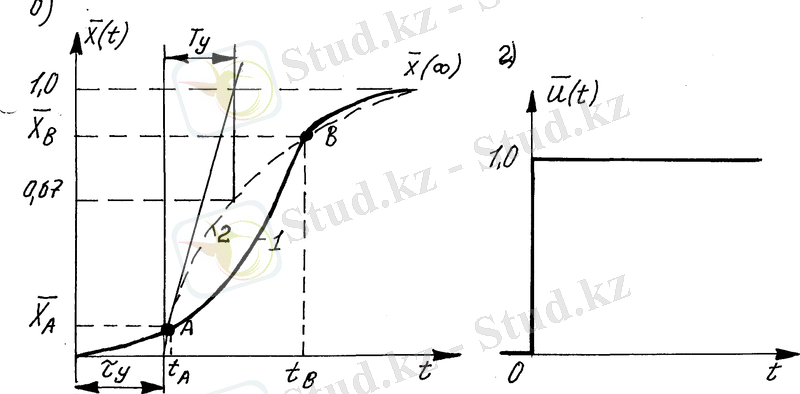
1. 5-сурет. Технологиялық объектілердің ауыспалы функцияларының сипаты жағынан ұқсас типтері
Кешігуі бар бірінші ретті инерциалды буынның дифференциалды теңдеуін былай көрсетеміз:
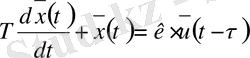 .
(1. 16)
.
(1. 16)
Кейбір объектілер көпсыйымдылықты болады, яғни жоғарғы ретті дифференциалды теңдеумен бейнеленед. Оларда коэффициент ретінде бірнеше уақыт тұрақтылары комбинациясы болады. Таза транспорттық кешігуі бар объектінің динамикасы, мына түрдегі сызықтық дифференциалды теңдеумен бейнеленеді:
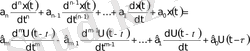 (1. 17)
(1. 17)
мұнда әрқашан
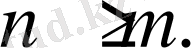
(1. 17) дифференциалды теңдеулерге, статикалық объектілердің S-түрлі ауыспалы процесс қисықтары (1. 5 ә -сурет) сәйкес келеді.
Астатикалық объектінің динамикалық қасиеттерін суреттеу кезінде де дифференциалдық теңдеулер қолданылады, бірақ бұл теңдеудің сол жақ бөлігінде а 0 х(t) мүшесі болмайды, ал оң жақ бөлігінде статикалық беріліс коэффициенті жоқ. Себебі, астатикалық объектілер, статикалық сипаттамаға ие болмайды (1. 5 б- сурет) .
Тау-кен өнеркәсібінің түрлі объектілердің динамикалық сипаттамаларын практика жүзінде бағалау тәжірибесі, олардың төменде берілген дифференциалды теңдеулердінің бірімен ұсынылады:
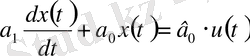 ;
;
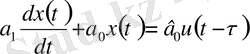 ;
;
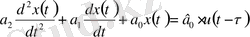 ; (1. 18)
; (1. 18)
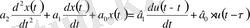 ;
;
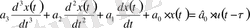 ;
;
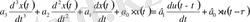 .
.
Егер жұмыс нүктесінің маңайында объектінің статикалық сипаттамасын сызықтандыру мүмкін болмаса, онда оны
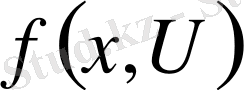 түрінде
түрінде
 және
және
 айнымалылардың сызықтық емес функциясы ретінде көрсету керек. Ол жағдайда (3. 16) дифференциалды теңдеу Коши формасында жазылғанда мына түрге енеді:
айнымалылардың сызықтық емес функциясы ретінде көрсету керек. Ол жағдайда (3. 16) дифференциалды теңдеу Коши формасында жазылғанда мына түрге енеді:
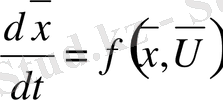 (1. 19)
(1. 19)
Көп өлшемді объектілерднің динамикасы, кейбір локалды аумақта, нормальды формада дифференциалды теңдеулердің жүйесі ретінде жазылуы мүмкін:
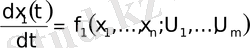 ;
;
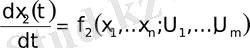 ; (1. 20)
; (1. 20)
.
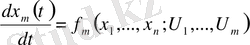 .
.
Осылайша, технологиялық операциялардың статикалық тәртібін сипаттайтын математикалық моделдер, (3. 5) түріндегі алгебралық теңдеумен анықталады. Ал осы операциялардың динамикалық моделін, (3. 18) түріндегі дифференциалды теңдеумен немесе (3. 20) түрінде көрсетуге болады. Технологиялық объектінің математикалық моделін осылайша келтіру, автоматты басқару жүйелерін синтездеуге мүмкіндік береді.
1. 2. Өндіріс басқару объектілерінің модельдерін алу әдістері
Тау-кен технологиясының объектісі ретінде технологиялық аппараты немесе олардың, бірден-бір типтік операциясын жүзеге асыратын жиынтығын түсінуге болады. Егер объект үшін басқару жүйесі құрылса, онда оны -
басқару объектісі
деп атайды. Бұл жағдайда, объектіге сезімтал элементтер (бергіштер) жатады. Бұл элементтер шығысы басқарылатын айнымалылар
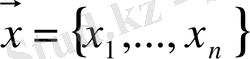 векторының жағдайын бақылайды. Сонымен қатар, кіріс басқарылатын
векторының жағдайын бақылайды. Сонымен қатар, кіріс басқарылатын
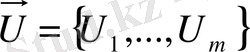 айнымалы векторының жағдайын өзгертетін реттеуші органдар жатады (1. 1-сурет) . Басқару объектісінің контурлары, басқару жүйесін құрастырушының алдына қойған негізгі мақсатына тәуелді.
айнымалы векторының жағдайын өзгертетін реттеуші органдар жатады (1. 1-сурет) . Басқару объектісінің контурлары, басқару жүйесін құрастырушының алдына қойған негізгі мақсатына тәуелді.
Технологиялық процестің басқару жүйесін құру, басқару объектілерінің моделімен тығыз байланысты. Технологиялық процесті басқарудың локальдық (қарапайым) жүйесін құру кезінде, басқару объектілерінің моделі ретінде статикалық және динамикалық сипаттамалар тұрады. Барлық технологиялық желіні басқаруда, объектілер арасындағы байланысты, басқару объектінің модель жиынтығын өзіне енгізетін күрделі модельдерді қолдану қажет.
Басқару объектісінің әрбір нақты моделі, жүріп жатқан физикалық процестердің көрінісі. Басқару объектінің моделін шартты түрде екіге бөлуге болады: физикалық және математикалық.
Физикалық модельдерде - басқару объектісіне тән құбылыстар жүруі қажет. Әдетте, модель объектіден геометриялық шамаларымен және
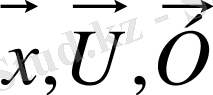 айнымалыларының өзгеру диапазонымен ерекшеленеді. Осындай модельдерді құру, объекті мен модельде өтетін процестердің сәйкес келу деңгейі бағалауға байланысты белгілі бір қиындықтарды жеңуді талап етеді. Бұл бағалау, ұқсастық теориясының теоремаларымен негізделеді.
айнымалыларының өзгеру диапазонымен ерекшеленеді. Осындай модельдерді құру, объекті мен модельде өтетін процестердің сәйкес келу деңгейі бағалауға байланысты белгілі бір қиындықтарды жеңуді талап етеді. Бұл бағалау, ұқсастық теориясының теоремаларымен негізделеді.
Физикалық модельдердің басқа тобына, объектінің физикалық табиғатына қарағанда, басқаша физикалық табиғатқа ие модельдер жатады. Бұл жағдайда, ұқсастық принципінің орнына, эквиваленттік принципі қолданылады. Эквиваленттілік шарттар орындалса, объекті теңдеуі мен модель теңдеуі сәйкес келеді. Мұндай модельдерді - аналогтық деп атайды.
Басқару объектісінің математикалық моделі ретінде, объектіде өтіп жатқан құбылыстың маңыздылығын көрсететін, алгебралық немесе дифференциалдық теңдеулер, теңсіздік, логикалық шарттар, операторлар, т. б. түріндегі жүйе қабылданады. Олар нақты бір алгоритмнің көмегімен, кірістегі
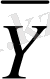 басқарылмайтын және
басқарылмайтын және
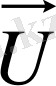 басқарылатын айнымалылар өзгерген кезде, объектінің жағдайын көрсететін
басқарылатын айнымалылар өзгерген кезде, объектінің жағдайын көрсететін
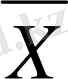 векторының өзгерісін болжауға мүмкіндік береді.
векторының өзгерісін болжауға мүмкіндік береді.
Математикалық модельдің ең негізгі қасиетіне, оның мағыналылығы жататынын көреміз, яғни зерттелетін объектінің маңызды жағын көрсету қабілеттігі.
Басқару объектілерін математикалық модельдеу кезінде, математикалық модельді құрастырады, оның шешімін табады және зерттелетін процеске моделдің адекваттығын тексереді.
Модель алудың аналитикалық әдісі - модельделетін объектіде жүретін процестерді сандық және сапалық түрде бағалауға негізделген. Бұл әдіс процестің физика-механикалық (немесе басқа) маңызын білуге; процестегі байланысты көрсететін математикалық теңдеулер жиынтығын математикалық модель түрінде көрсетуге мұмкіндік береді; математикалық модельдің сәйкестену деңгейін анықтауға мүмкіндік береді. Мұндай модельдер үлкен ортақтықпен ерекшеленеді, олар тек бір ғана нақты объект жөнінде емес, жалпы осындай объектілер класынан басқару жүйелерін жобалау кезінде аса құнды болады.
Тау-кен технологиясының математикалық модельдерін аналитикалық әдіспен алу, тәжірибиеде қолайлы емес. Себебі, тау-кен өнеркәсібінің процестері әдетте сызықсыз, көп шамалы, стационарлы емес. Көп жағдайда, объект жұмысының динамикалық және статикалық режимінде, кіріс пен шығыстағы айнымалылар арасындағы байланыс формасы жайлы ақпарат түспейді. Осының барлығы, аналитикалық әдіспен үйлес моделін алуды қиындатады.
Математикалық модельдерді анықтаудың эксперименталдық әдісі екіге бөлінеді: активтік және пассивтік . Активтік экспериментті жүргізу кезінде зерттеліп отырған объектінің кірісіне белгілі бір түріндегі u басқару сигналдары беріледі, ал содан кейін шығыстағы айнымалылардың өзгерісі (1. 6-сурет) белгіленеді. Мұндай сигналдарға объектінің кірісіне қолмен немесе техникалық құрылғының көмегімен берілетін жоспарланатын ықпал (ЖЫ) жатады. Кіріс u сигналдары - кездейсоқ және ұдайы болып бөлінеді. Ұдайы сигналдарға - апериодтық (сатылы функция 2 және импульстік ықпал 3) және периодтық (синусоидалылық ықпал 4 немесе тік бұрышты толқын 1) жатады. Берілген жоспарланатын ықпал - объектінің динамикалық сипаттамаларын анықтаға, ал ықпал 1 -статикалық сипаттамаларын анықтау үшін қолданылады. Кірістегі кездейсоқ әсер етуші u арнаулы шу генераторымен құрылады. Оларды қолдану арқылы, объектілердің динамикалық сипаттамаларын анықтау әдісі жеңілдейді.
Объектінің кірісінде активтік эксперимент нәтижесінде оның шығысында Х-тың экспериментальдық мәнін алады, одан кейін аналитикалық тұрде, математикалық әдістермен үйлестілігі анықталады.
Пассивтік экспериментті жүргізу кезінде объектінің шығысындағы айнымалы шаманың және кірісіндегі айнымалы u шаманың кездейсоқ ықпалын (СВ) ұдайы белгілеп отырады. u және Х экспериментальдық шамаларын өңдеу - кіріс пен шығыс кездейсоқ сигналдарының статикалық сипаттамаларын анықтауға, солар арқылы объектінің динамикалық және статикалық сипаттамаларын есептеуге әкеледі.
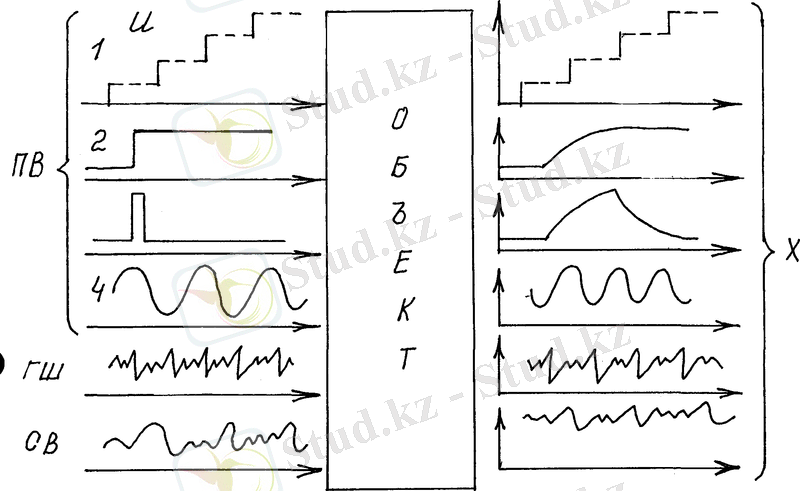
1. 6-сурет. Активтік және пассивтік эксперимент арқылы эксперименталдық әдіспен объектінің математикалық модельдерін алу схемасы
Экспериментальды-аналитикалық әдіс кезінде біріншіден, аналитикалық модельді құрады, содан кейін математикалық модельге кіретін коэффициенттерді дәлелдеу үшін, нақты бір объектіде эксперименттік зерттеу жүргізеді.
1 . 2. 1. Математикалық модельдер алудың аналитикалық әдісі
Математикалық модельдердің аналитикалық әдісін құру - бізге белгілі материалды дүниенің заңдарына негізделген. Осындай модельдерді құру кезінде, технологиялық процесті айтарлықтай дәріптеу қажет, өйткені ол технологиялық процесті құрайтын элементар құралға бөліп, олар жайлы салыстырмалы түрде математикалық суреттеу және зерттеу гипотезасы жүргізіледі. Объектілерді аналитикалық түрде модельдеу әдісі мына сатыдан тұрады:
- процесті зерттеу;
- жеткілікті түрде оны дәріптеу;
- материалдық және энергетикалық баланс теңдеуін, процестің кинетикалық теңдеуін, гидравликалық, т. б. теңдеулерін құру;
- теориалық модель мен процестің үйлестігін анықтау.
Объектінің статикалық сипаттамасын анықтау үшін, материалдық және энергетикалық баланс теңдеуін жиі қолданады:
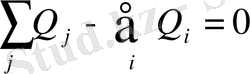 ;
;
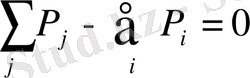 (1. 21)
(1. 21)
мұндағы Q j , Q і және P j , P і - объектіге берілетін, әрі одан алынатын заттардың шығын энергия ағындары. (1. 21) теңдеуі (1. 5) немесе (1. 13) түріне айналады.
Объектінің дифференциалдық теңдеуін алу үшін:
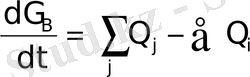 ;
;
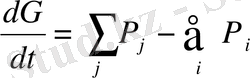 (1. 22)
(1. 22)
қалыптанбаған режиміндегі энергияның немесе заттың жиналу процесін сипаттайтын өрнек қолданылады. Бұл дегеніміз - объектідегі шығын (Q j ) өзгерсе, объектіде G В затын жинау процесі басталып, шығу координаттары өзгеріске ұшырайды, мысалы Q і . (1. 22) өрнегі (1. 17) немесе (3. 20) түріне келтіріледі.
1. 7-суретінде 1 құбырдан ағатын сұйықтың шығынын қалыптандыратын, автоматты жүйе келтірілген.
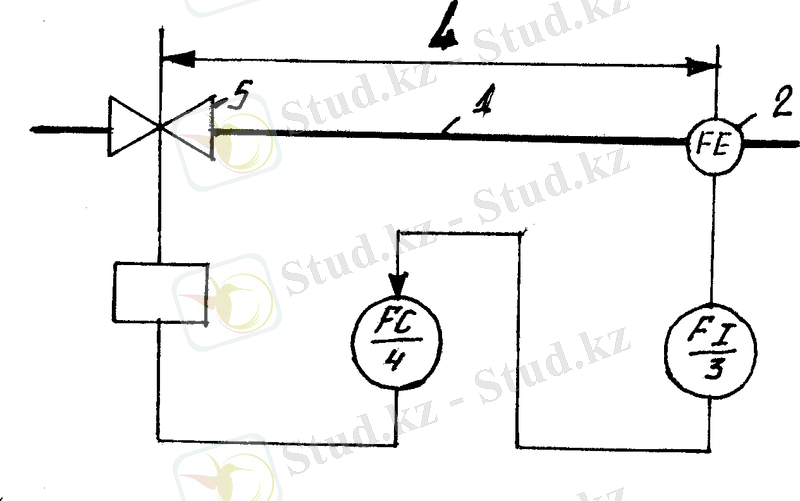
1. 7-сурет. Сұйықтық шығынын тұрақтандыру жүйесі
1 - құбыр; 2 - өлшеу құрылғысы; 3 - екінші аспап, 4 - реттегіш; 5 - реттеуші орган
Автоматтандыру объектісіне
L
ұзындықты құбырдың 1 саласы жатады. Осы объектінің динамикалық және статикалық сипаттамаларын аналитикалық әдіспен анықтаймыз.
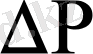 қысымның түсуі мен құбырдағы сұйықтың
қысымның түсуі мен құбырдағы сұйықтың
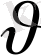 жылдамдығы арасындағы байланыс белгілі, ол:
жылдамдығы арасындағы байланыс белгілі, ол:
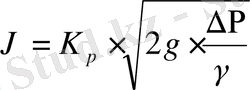 ; (1. 23)
; (1. 23)
мұндағы g - еркін құлау үдеуі;
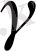 - сұйық тығыздығы;
- сұйық тығыздығы;
К р - шығыс коэффициенті.
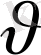 жылдамдығы, кесінді
S
ауданының кері көлеміне тең болатын коэффициентімен, құбырдан өтетін сұйықтың шығынына (Q) пропорционал болғандықтан, қысым күшінің балансын
жылдамдығы, кесінді
S
ауданының кері көлеміне тең болатын коэффициентімен, құбырдан өтетін сұйықтың шығынына (Q) пропорционал болғандықтан, қысым күшінің балансын
 Р•S және гидродинамикалық қарсыластықтың теңдеуін былай жазуға болады:
Р•S және гидродинамикалық қарсыластықтың теңдеуін былай жазуға болады:
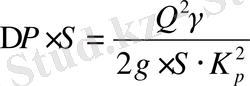 . (1. 24)
. (1. 24)
(1. 24) өрнегі - құбырдың статикалық сипаттамасы, өйткені ол құбыр мен сұйықтың сипаттамалары-
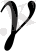 , S, К
р
, кірістегі
, S, К
р
, кірістегі
 Р, шығу Q айнымалысы арасындағы өзара тәуелділікті көрсетеді.
Р, шығу Q айнымалысы арасындағы өзара тәуелділікті көрсетеді.
Егер түсірілетін
 РƒS
күші құбырдың гидродинамикалық кедергісінен басым түссе, онда ағын үдеулікпен қозғала бастайды. Сондықтан, жұмыстың қалыптанбаған тәртібі кезіндегі күш теңдеуі былай жазылады:
РƒS
күші құбырдың гидродинамикалық кедергісінен басым түссе, онда ағын үдеулікпен қозғала бастайды. Сондықтан, жұмыстың қалыптанбаған тәртібі кезіндегі күш теңдеуі былай жазылады:
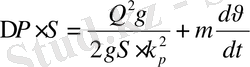 ; (1. 25)
; (1. 25)
мұндағы
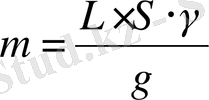 - құбырдағы сұйықтың массасы, кг.
- құбырдағы сұйықтың массасы, кг.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz