Кристалдық химия

Пән: Химия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 90 бет
Таңдаулыға:

Қозыкеева Р. А.

К Р И С Т А Л Д Ы Қ Х И М И Я

ШЫМКЕНТ-2007

ӘОЖ 544. 228(0758)

Қ 59

Қ. А. Ясауи атындағы Халықаралық Қазақ-Түрік университеті

Шымкент иниституты Ғылыми кеңесінің шешімімен баспаға

ұсынылған ( хаттама N 2 26. 10. 2007ж )

Құрастырған: Қозыкеева Р. А.

Пікір жазғандар: А. П. Әуешов- Қ. А. Ясауи атындағы ХҚТУ-нің химия ғылымдарының докторы, профессор.

Б. Ш Кедельбаев- М. Ауезов атындағы ОҚМУ-нің химия ғылымдарының докторы.

А. Д. Асильбекова- Қ. А. Ясауи атындағы ХҚТУ-нің техника ғылымдарының кандидаты, доцент.

Жоғары оқу орындарының студенттеріне арналған оқулықта кристалдық химияның негізгі бөлімдері: кристалл, кристалл затар және кристаллография туралы түсінік, кристалдардағы екі қырлы бұрыштардың тұрақтылық заңы, кристалдардың симметриясы, көп қырлы кристалдардың формасы, бүтін санадар заңы және көп қырлы кристалдардың аналитикалық әдістерін баяндау, Е. С. Федоровтың кристалдар структурасының теориясы қарастырылған.

ISBN 9965-898-70-6

 Қозыкеева Р. А.

“Алтын алқа”, 2007ж.

КІРІСПЕ

Оқулық Қазақстан Республикасының Білім және Ғылым министрлігінің университет студенттеріне арнап бекіткен кристалдық химия пәнінің бағдарламасына сәкес жасалынды.

Жаратылыстану ғылымдарының бірі болып есептелетін кристалдық химия пәнінен қазақ тілінде жазылған оқулықтар тіпті жоқ десекте болады. Оқулықты қазақ тілінде дайындау барысында ортақ терминдер қолданылды.

Ұсынылып отырған оқулықта кристалдық химияның негізгі бөлімдері: кристалл, кристалл затар және кристаллография туралы түсінік, кристалдардағы екі қырлы бұрыштардың тұрақтылық заңы, кристалдардың симметриясы, көп қырлы кристалдардың формасы, бүтін санадар заңы және көп қырлы кристалдардың аналитикалық әдістерін баяндау, Е. С. Федоровтың кристалдар структурасының теориясы қарастырылған.

Жақсы қырланған кристалдар өте ертеден-ақ адамзат көңілін өзіне аударған. Олардың табиғатта табылуы ертеректе қиял-ғажайып түсініктермен байланыстырылды. Жақсы түзілген кристалдар ерекше мистикалық қасиеттерді иеленеді. Олар аурудан сауықтыруға немесе керісінше кейбір ауруларды туғызуға, адам тағдырына ықпал етуге т. б. қабілетті деп есептеледі. Осылайша кристалдарға ерекше көңіл аудару оларды коллекциялауға мүмкіндік туғызды, олардың пішінін егжей-тегжейлі бақылауға және ғылыми жинақтап қортындылауға алып келеді.

Кристаллография, ботаника-өсімдіктердің алуан түрлілігімен, химия-химиялық қосылыстарымен және т. б. шұғылданатын сияқты кристалдардың сан алуан түрлерін зерттеумен шұғылданады. Ол осы алуан түрліліктің бірлігінің белгілерін (заңдарын) анықтайды; дара кристалдар мен кристалдық агрегаттардың (структурасын) құрылысын және қасиетін зерттейді.

Кристаллография-кристалдарда жүретін құбылыстарды, кристалдың қоршаған ортаға әсерін, қандайда бір әсер ету арқылы кристалдарда жүретін өзгерістерді зерттейді. Бір сөзбен айтқанда кристаллография кристалл заттарды жан-жақты зерттейтін ғылым болып табылады.

Кристаллография-химиямен, физикалық химиямен және физикамен тығыз байланысты. Сондай-ақ кристаллографияның геологиялық пәндерімен, бәрінен бұрын минероллогиямен, геохимиямен және петерографиямен де байланысты. Ертеректе кристалдар сирек кездеседі деп саналады. Шынында, табиғатта ірі біртекті кристалдардың табылуы-сирек құбылыс. Бірақ ұсақ кристалды заттар өте жиі кездеседі. Барлық тау жыныстары: граниттер, құмдар, әктастар және т. б. кристалдар. Металлургия өнеркәсібінің шикізаты болып табылатын барлық рудалар кристалды болып келеді. Сондай-ақ, руданы өңдеу нәтижесінде алынған металлургия өнеркәсібінің өнімдері-барлық металдармен олардың қорытпалары кристалды. Барлық құрылыс материалдары да ұсақ кристалдардан тұрады.

Химия өнеркәсібінің көптеген қатты өнімдері (ашудас, селитра, купорос, сода, нафталин және т. б. ) де кристалды, ал сұйық химиялық өнімдер, мысалы мұнай өндірісінің бірқатар өнімдерін немесе органикалық емес қышқылдарды кристалды күйде өте төменгі температурада оңай алуға болады. Зерттеу әдістерін жетілдіру барысында (алғашқыда визуальді әдістер, сосын микроскопия, рентгендік талдау, электронография және т. б. ) осыған дейін аморфты деп саналған заттар кристалды болып шықты.

Қазір біз ағзаның кейбір бөліктерінің, мысалы көздің мөлдір қабығының кристалды екендігін білеміз. Белоктар мен вирустарды рентгеноструктуралық және кристаллохимиялық зерттеу ерекше ғылыми бағыт алды. Ары қарай химия мен биологияда кристаллографиялық әдістерді енгізу күмәнсіз.

Сондықтан жоғары оқу орындарының және факультеттерінің студенттеріне кристаллографияның және ерекше кристаллохимияның негіздерін білуі қажет.

I-БӨЛІМ. КРИСТАЛЛ, КРИСТАЛЛ ЗАТТАР ЖӘНЕ КРИСТАЛЛОГРАФИЯ ТУРАЛЫ ТҮСІНІК.

Табиғаттағы заттар әдетте негізінен үш агрегаттық күйдің бірінде болады: газ тәрізді, сұйық немесе қатты түрде кездеседі. Соңғысы, шамамен кристалды күймен бірдей болып табылады. Әрбір күй бір-бірімен салыстырғанда материал бөлшектерінің қозғалысының сипатымен ерекшеленеді.

Газдарда ретсіз қозғалыс байқалады. Материал бөлшектердің - молекула немесе атомдардың бір-біріне тартылуын газдарда қолдануға болады және алғашқы жуықтауда ондай бөлшектер өзара соқтығысу кезінде шарлардың серпімділік заңы бойынша тебіледі деп санауға болады.

Сұйықтарда бөлшектердің қозғалысы анағұрлым баяу, өзара әсер ету күшінің-тартылу күшінің әсерінен уақытша реттілік сақталады. Бөлшектердің арасындағы ара қашықтық газдардағы ара қашықтықпен салыстырғанда біршама қысқарған, оны газдар мен сұйықтардың түрлі сығымдалғыштығы бойынша айтуға болады.

Кристалдарда материал бөлшектер, мысалы молекулалар, бір-біріне қатысты бейімделген. Нәтижесінде бұл кристалл белгілі бір формада, қандайда бір көп қырлы дене түрінде болады. Материал бөлшектер тепе-теңдік жағдайының төңірегінде жылу тербелістерін жасайды. Егер температура кристалдық балқу температурасынан алшақ болса, онда ереже бойынша бөлшектер шамамен ешқашан үдемелі қозғалысқа түспейді. Кристалдың, сұйықтан айқын айырмашылығы осында.

Материал бөлшектердің тартылу күшінің табиғаты барлық агрегаттық күйде әрқашан да электрлі. Сонымен, молекулалық кристалда, яғни бейтарап бөлшектерден құрылған молекула-кристалда бұл бөлшектердің салыстырмалы бағыты, мысалы оларда электрлі дипольдердің болуымен байланысты болуы мүмкін (1-cурет) .

Зат ретсіз (cұйық) күйден ретті кристалды күйге өтуі үшін біраз уақыт керек. Бұл уақыт кристалдандыру уақыты деп аталады. Егер кристалдау үшін қажет уақытқа қарағанда, салқындатау мен қатаю тез жүретін болса, онда бөлшектері сұйықтардағы сияқты ретсіз күйде қалатын аморфты немесе шыны тәрізді дене түзіледі.

1-сурет. Көп қырлы кристалдардың проекциясы.

1. 2. Кристалдардың негізгі қасиеттері.

Кристалдың негізгі қасиеттерінің бірі анизотропия болып табылады. Бұл термин бағытқа байланысты қасиеттердің өзгеруімен түсіндіріледі.

Сонымен, мысалы, ас тұзының кристалынан 1мм ² көлденең қима арқылы түрлі бағытта стерженьдер кесіп алып, оларды үзіп тастасақ, онда олардың беріктігі әр түрлі болады. Сонымен, кубтың бір қырына перпендикуляр және басқаларына параллель стержень оған 570 г/мм ² - тең күш түсірілсе үзіледі (2-сурет) . Куб қырының диогналына параллель кесіп алынған осындай стержень 1150 г/ мм ² күш түсірілген кезде үзіледі. Кубтың кеңістіктегі диогналы бойынша кесіп алынған стержень аса берік болып табылады. Үзілуі 2150 г/мм ² асатын күш түсірілген кезде жүреді. Егер біз мұндай стержендерді шыныдан немесе қандай да бір басқа изотропты денеден кесіп алсақ, онда олар бағытына қарамастан бірдей күш түсірілген кезде үзілер еді.

Анизотропты заттардың изотропты затардан айырмашылығы да осында.

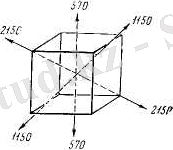
2-сурет. Ас тұзы кристалының қатылығының бағытқа тәуелділігі.

Сонымен бірге кристалдар біртекті дене болып табылады. Кристалл заттардың біртектілігі оның бірдей формадағы және бірдей шамадағы екі бөлігіде өзінің қасиеттері бойынша бірдей екендігінде (3-сурет) .

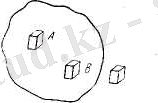
3-сурет. Кристалл заттардың біртектілігі келтірілген.

Кристалл заттардың үшінші маңызды қасиеті өздігінен қырлануға қабілеттігі деп аталатын жазықтық көп қырлар түзуге мүмкіншілігі болып табылады. Сондай-ақ бұл қасиет ішкі (атомдық) реттіліктің нәтижесі болып табылады. Егер кристалл өсу кезінде механикалық кедергілерге кезікпесе, онда ол дөңес көп қырлы түрінде өседі.

Сонымен, кристалдың ең маңызды қасиеті оның симметриясы болып табылады. Ол туралы төменде қарастырылады.

1. 3 Кристалл және кристалдық заттар.

Кристалдық күйдің газ тәрізді және сұйық күйден айырмашылығы оның анағұрлым сан алуандығында. Құрамы және пішіні бойынша бірдей молекулалар кристалда түрлі әдістермен буып - түйілуі мүмкін (4 а, г -сурет)

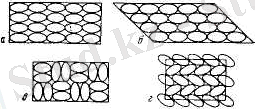
4-сурет. Бірдей бөлшектердің әр түрлі буып-түйілуі.

Заттың физика-химиялық қасиеттері буып-түю әдістеріне байланысты. Осылайша химиялық құрамы бойынша бірдей заттар іс жүзінде түрлі физикалық қасиеттерге ие бола алады. Мұндай әр түрлілік заттардың сұйық күйіне тән емес, ал газдар үшін тіпті де мүмкін емес.

Мысалы, егер кәдімгі ас тұзын алар болсақ, онда тіпті микроскоптың көмегінсіз жекелеген кристалдарды көруге болады. Әрбір кристалл NаСI заты, бірақ ол сол уақытта бөлек кескінге де ие. Ол үлкен немесе кіші, куб болмаса тік бұрышты-параллелепипедті, түрліше қырланған және де т. б. болуы мүмкін.

Сұйықта жекелеген ерекшелікті тамшыны көре алмайсыз, ал кристалл заттарда олар көрінеді.

Егер микроскопен тегістеліп қырналған металды қарайтын болсақ (5-сурет), онда оның өзіне тән жекелеген кристалдары өзіндік кескіндерімен байқалады.

5-сурет. Қырналған металдың кескіні.

Егер біз кристалдың ерекшелігі бар бірдей жекелеген кристалды атап көрсеткіміз келсе, онда біз оны монокристалл деп атаймыз. Көптеген кітаптарда кристалл термині дара кристалл ретінде де кристалл зат ретінде де түсіндіріледі. Кейде біз тоқталған көптеген кристалдарды ерекшелеп көрсету үшін кристалдық агрегат терминін пайдаланамыз. 5-суретте көрсетілген тегістеліп өңделген металл кристалдық агрегатқа жақсы мысал болып табылады. Онда жекелеген кристалдар қырланбаған дерлік. Бұл көп жағдайда балқыманың көптеген нүктелерінде бір мезгілде басталып, тез кристалдану кезінде орын алады. Көбейіп келе жатқан кристалдар бір-біріне кедергі келтіреді және олардың әрқайсысының дұрыс қырлануына жол бермейді.

1. 4. Кристаллография.

Ол осы алуан түрліліктің бірлігінің белгілерін (заңдарын) анықтайды; дара кристалдар мен кристалдық агрегаттардың (структурасын) құрылысын және қасиетін зерттейді. Кристаллография − кристалдарда жүретін құбылыстарды, кристалдың қоршаған ортаға әсерін, қандайда бір әсер ету арқылы кристалдарда жүретін өзгерістерді зерттейді. Бір сөзбен айтқанда кристаллография кристалл заттарды жан-жақты зерттейтін ғылым болып табылады.

Кристаллография үш бәлімнен тұрады: геометриялық кристаллография, химиялық кристаллография (кристаллохимия) және физикалық кристаллография (кристаллофизика) . Соңғы екі бөлім бір-бірінің қатысынсыз зерттелуі мүмкін, бірақ екеуі де алғашқысына негізделеді, онсыз оларды ұтымды баяндап беру мүмкін емес.

Басқа кристалл емес заттардан кристалл заттардың айырмашылығы ол ретті атомдық структураға ие және анизотропты екендігіне қарай кристаллография әдістері басқа ғылымдардың әдістерінен айқын ерекшеленеді. Симметрия кристалдардың сыртқы пішінінде, олардың структурасында, кристалдарда жүретін физикалық құбылыстарда, кристалдардың қоршаған ортаға әсер етуі кезінде, сыртқы күштердің әсерінен кристалдарда болатын өзгерістерде айқын білінеді. Сондықтан кристаллография әдістерінің ерекшелігі барлық жағдайда симметрия принципін жүйелі түрде қолдану болып табылады. Осы аса өзгеше әдісінің арқасында кристаллография нақты жағдайларда, зерттеу тақырыбы және басқа ғылымдармен міндеті, мақсатының ішінара сәйкес келуімен байланысқан дербес ғылым болып табылады.

Кристалл заттарды оның түзілу процессінсіз, газ тәрізді және сұйық фазалармен байланысынсыз зерттеуге болмайды. Бұл процестерді физикалық химия зерттейді, өйткені кез-келген процесс немесе тепе-теңдік күйі ортаның физика-химиялық жағдайына тәуелді. Кристалл заттарда атомдар мен молекулалардың салыстырмалы орналасуы сол атомдардың сапасына, олардың химиялық табиғатына байланысты. Сондықтан ол химиямен, әсіресе стерохимиямен тығыз байланыста. Атомдар мен молекулалар кристалдарда геометриялық дұрыс комплекстер түзеді. Олардың жиынтығы көп қырлар түрінде кристалдың пішінін анықтайды. Көп қырларды математика, бірінші кезекте геометрия зерттейді. Әрине, кристаллографияның физиакмен, әсіресе оның қатты денелердің түрлі қасиеттерін зерттеумен шұғылданатын бөлімдерімен байланысы дәлелдеуді қажет етпейді. Соңғы жылдары оптикалық, электірлік, механикалық және т. б. түрлі қасиеттері бар монокристалдарды қолданатын өнеркәсіптер қарқынды дамып келеді.

Кристаллографияның химиямен, физика-химиямен және физикамен байланысының тығыздығы соншалықты бұл ғылымдардың арасына тіпті шартты түрде де шекара жүргізуге мүмкіндік бермейді.

Кристаллографияның геологиялық пәндерімен, бәрінен бұрын минероллогиямен, геохимиямен және петерографиямен де байланысты. Минералдың басым мөлшері кристалдық, өйткені олардың көпшілігі жақсы түзілген кристалл түрінде белгілі, бірақ өз тарихында ертеректе кристаллография минералогияның бөлімі ретінде қарастырылады. Кристалдың сыртқы пішіні осы кезге дейін минералдың маңызды диагностикалық белгісі болып табылған.

Ал минералдың атомдық структурасын зерттеу оларды топтау қазіргі заманың негізі болып табылады. Зерттеудің кейбір кристаллографилық әдістері геологиялық пәндерде маңызды роль атқарады; мысалы кристалооптикалық талдау қазір петрографияның негізгі әдісі болып табылады.

1. 5. Кристалл заттардың таралуы.

Ертеректе кристалдар сирек кездеседі деп саналады. Шынында, табиғатта ірі біртекті кристалдардың табылуы-сирек құбылыс. Бірақ ұсақ кристалды заттар өте жиі кездеседі. Барлық тау жыныстары: граниттер, құмдар, әктастар және т. б. кристалды. Металлургия өнеркәсібінің шикізаты болып табылатын барлық рудалар кристалды. Сондай-ақ, руданы өңдеу нәтижесінде алынған металлургия өнеркәсібінің өнімдері-барлық металдармен олардың қорытпалары кристалды. Барлық құрылыс материалдары да ұсақ кристалдардан тұрады.

Химия өнеркәсібінің көптеген қатты өнімдері (ашудас, селитра, купорос, сода, нафталин және т. б. ) де кристалды, ал сұйық химиялық өнімдер, мысалы мұнай өндірісінің бірқатар өнімдері немесе органикалық емес қышқылды да кристалды күйде өте төменгі температурада оңай алуға болады. Зерттеу әдістерін жетілдіру барысында (алғашқыда визуальді әдістер, сосын микроскопия, рентгендік талдау, электронография және т. б. ) осыған дейін аморфты деп саналған заттар кристалды болып шықты.

1. 6. Кристаллизация монокристалдар өнеркәсібі.

Кристаллографияда-кристализация ерекше орын алады. Газ тәрізді, сұйық және қатты фазалардан кристалдар алу процессі, қазір қарқынды түрде зерттелуде. Олар тек фазалық өту теориясын дамыту үшін ғана қажет емес. Қазір дүние жүзінде микрокристалдар өнеркәсібі қарқынды өсуде. Кристалдардың көп түрлілігі, олардың өзгеше қасиеттері қазіргі уақытта ғылым мен техникада тиімді қолданылуда. Мысалы ультракүлгін, инфрақызыл сәулелерді өткізетін оптикалық призмалар мен линзалар дайындау үшін NаCL, LіF, СаF ₂ , SiO ₂ т. б. монокристалдар қолданылатыны белгілі. Бұл заттарды ірі жетілген монокристалдар түрінде алу өте қиын міндет. Қазіргі уақытта техника бізден әр күн сайын жаңа монокристалдардың өте көп, үлкен мөлшерін талап етеді. Өнеркәсіпте ашудас пъезокристалдары SiO ₂ , сагнет тұзы, C ₄ Н ₄ О ₆ КNа · 4Н ₂ О т. б. кең тарады. Дәл жүретін құралдар үшін мыс сағаттар үшін подшипниктер рубиннен Аl ₂ О ₃ аздаған Сr ₂ О ₃ қоспасынан дайындалады. Рубин монокристалдарының дамуында жаңа серпіліс, оларды лазер ретінде қолдана бастағаннан кейін жүрді. Ғылымда және техникада квантты генераторларды, люминесцентті кристалдар және жартылай өткізгіштер монокристалдары үшін түрлі кристалдарды қолдану бүтін бір дәуірді құрайды. Әдетте кристалдарды алу аса таза заттарды қолданумен байланысты, сондықтан кристаллограф, химиктер және физиктердің мақсаттары бұл мәселеде бір жерге жиналды. Ендеше, монокристалдар өндірісі саласында жұмыс істейтін мамандарға, сондай-ақ осындай жұмыстарға дайындайтын химиялық жоғары оқу орындарының және факультеттерінің студенттеріне кристаллографияның және ерекше кристаллохимияның негіздерін білуі қажет.

II- БӨЛІМ. КРИСТАЛДАҒЫ ЕКІ ҚЫРЛЫ БҰРЫШТАРДЫҢ ТҰРАҚТЫЛЫҚ ЗАҢЫ.

2. 1. Кристалдардың сыртқы пішінін зерттеуге арналған алғашқы жұмыстар.

Жақсы қырланған кристалдар өте ертеден-ақ адамзат көңілін өзіне аударған. Олардың табиғатта табылуы ертеректе қиял-ғажайып түсініктермен байланыстырылды. Жақсы түзілген кристалдар ерекше мистикалық қасиеттерді иеленеді. Олар аурудан сауықтыруға немесе керісінше кейбір ауруларды туғызуға, адам тағдырына ықпал етуге т. б. қабілетті деп есептеледі. Осылайша кристалдарға ерекше көңіл аудару оларды коллекциялауға мүмкіндік туғызады, олардың пішінін егжей-тегжейлі бақылауға және ғылыми жинақтап қортындылауға алып келеді.

Біздің жыл санауымыздың 79- шы жылдарында-ақ Үлкен Плиний кристалдардың тік қабырғалылығы мен жалпақ қырлылығы туралы айтып өтті. Бұл қорытындыны геометриялық кристаллографияны алғашқы жинақтап қорыту деп есептеуге болады. Содан бері көптеген жүз жылдар бойы XVIII ғ. соңында геометриялық кристаллографияның маңызды заңы - кристалдардағы екі қырлы бұрыштардың тұрақтылық заңының ашылуына мүмкіндік берген материалдар баяу болса да үнемі жинақталып отырды.

Бұл заң 1783 табиғи кристалдардың бұрышын өлшеу бойынша Француз ғалымы Роме де Л ^' Илияның мол материалы жарияланды. Ол зерттеген әр заттың кристалдары үшін бірдей заттардың барлық кристалдарында сәйкес қырлардың арасындағы бұрыштар тұрақты болып табылатындығы туралы ереже сәйкес келеді. Роме де Л'Ильдің еңбегі, оның тауып өлшеген барлық заттарының кристалдары бұрыштарының тұрақтылық заңын кеңінен таратқандығында.

Бұл жұмыс оның бүкіл ұзақ өмірінің жемісі болып табылады. Ол өз жұмысының нәтижелерін Парижде ғалымдарға жүйелі түрде баяндап тұрды. Бұл хабарламалар кристаллография бойынша алғашқы лекциялары болып табылады.

Осыған қарап Роме де Л 'Ильден басқа кристаллографияның негізін салушылар болмады деп ойлауға болмайды.

Бұрыштардың тұрақтылық заңның ашылу тарихы екі ғасырға жуық ұзақ жолдардан өтті, бұл заң ашылудан бұрын барлық кристалды заттар үшін барлық еңбектер жинақталып тұжырымдалды. Мысалы, И. Кеплер 1615 қар ұшқында жекелеген сәулелердің арасындағы бұрыш 60 ^° - қа сақталғанын көрсетті. 1669 ж. Н. Стенсен гематит және кварц кристалдарындағы бұрыштардың тұрақтылық заңын ашты. Бір жылдан соң Э. Бартолин кальцит, 1695 ж Левенгук гипс кристалына осы заңды қолдануға болатындығына қорытынды жасады. Ол микроскопиялық зерттеу барысында кішкентай және үлкен гипс кристалдарының арасындағы сәйкес қырлардың бірдей болатындығын көрсетті.

Ресейде бұрыштардың тұрақтылық заңын 1749 ж. селитра, пирит, алмаз және басқа бірнеше миниралдардың кристалдары үшін М. В. Ломоносов ашты. Сонымен қатар Ломоносов селитраның молекулалық құрылысы туралы қисынды болжамдарын ұсынды. Лабораторияда алынған химиялық қосылыстардың кристалдарының көптеген зерттеулерін Ресей ғылым академиясында химия кафедрасы бойынша Ломоносовтың жолын қуушы Т. Е. Ловицев жүргізді.

Мысал ретінде Роме де Л' Иль жұмыстарынан SiO ₂ кварц кристалдарының формасы бойынша түрлі суреттерді қарастырамыз. Барлық кристалдар сәйкес қырлардың арасындағы бұрыштары тұрақты болатын қасиетке ие.

Жекелеген дара кристалдарда қырлар түрлеше дамуы мүмкін. Бірақ, біз сәйкес қырлар арасындағы бұрышты өлшейтін болсақ,

(мысалы а , в және с 6- сурет) онда бұл бұрыштардың мәндері кристалл формасына қарамастан тұрақты күйде қалады.

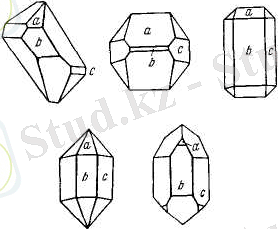
6-сурет

Сурет Роме де Л Ильдің кітабынан алынған( 1783 ), бұрыштардың тұрақтылық заңын суреттейтін мысалы кварц кристалдарының әр түрлі формасы. Біріңғай қарапайым формасын а , б және с әріптеріне сәйкес белгіленген.

2. Кристалдарды өлшеу әдістері.

Кристалдарды өлшеу барысында Роме де Л Иль барлық жұмыстарын өзінің оқушысы Каранжо ойлап тапқан қолданбалы

( 7-cурет ) гониометрдің көмегімен жүргізеді.

Бұл құрал ортасы арқылы өтетін осьті айналатын сызғышты транспортирден тұрады. Кристалдың бір қыры транспортирдің шетіне, екінші қыры жылжымалы сызғышқа тиіп тұратындай етіп қойып, кристалдың қырларының арасындағы сәйкес екі қырлы бұрышқа есептеп транспортир шкаласы бойынша жүргізеді.

6-суретте бейнеленген кварц кристалындағы а және в қырларының арасындағы бұрышты өлшеу көрсетілген. Қолданбалы гониометрдің көмегімен кристалдарды өлшеудің дәлдігі үлкен емес екендігі айқын. Ол шамамен жарты градусқа жетеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.