Қатты денелер беріктілігінің кинетикалық концепциясы: құрылымы, ақаулары және қирау механизмдері


Мазмұны
Кіріспе . . . 3
І - Тарау; Әдебиеттерге шолу
1. 1 Қатты денелердің ішкі құрылымы . . . 10
1. 2 Моно және поли кристалдық қатты денелер . . . 16
1. 3 Химиялық элементтердің кристалдық құрылымы . . . 18
1. 4 Полиморфизм құбылысы . . . 23
1. 5 Кристалдағы құрылым жетіспеушілігі және ақаулары . . . 26
1. 6 Қатты денелердің механикалық және жылулық қасиеттері . . . 34
1. 7 Кристалдар ығысуының теориялық және практикалық беріктілігі . . . 43
ІІ - Тарау
2. 1 Зерттеу обьектісі . . . 70
2. 2 Қатты денелердің жарамдылық мерзімі және беріктілік кинетикалық концепсиясының негіздер . . . 73
Қорытынды . . . 80
Пайдаланылған әдебиеттер . . . 83
Кіріспе
Денелердің беріктілігін зерттеу проблемасы қайтадан қаралу барысына негізделген. Қайтадан қараудың екі негізгі себебі бар:
- біріншіден, дене қирау мәселені жаңа көзқараспен қарастырудың дамуы, қирау процесінде атом және молекулалардың жылулық қозғалысын есепке алу, яғни қирауды кинетикалық процес деп түсіну;
- екіншіден, әртүрлі физикалық және физика - химиялық әдістер атом малекулалық деңгейде жүктелген денелерде өтетін құбылыстарды анықтауда кеңінен қолдана бастауы.
әрине, беріктілік ғылымының дамуына материалдарға қойылатын талап пен қолдану мүмкіншіліктері тез өзгеруі, беріктілікті интентсивті түрде өзінің әсерін тигізеді және ғылыми нәтижелерді практикада қолшдануды қажет етеді.
Осы айтылған мәселелерді ескере отырып, беріктілік физикасының ғылымының ары қарай даму саласына жатқызуға болады. Жиналған эксперименттіңк мәліметтерге сүйене отырып, дененің механикалыққирауын кинетикалық деуге негіз тудыратынын қарастырып, осы бағыттағы проблемаларды талдау, беріктілікиің кинетикалық концепциясын ары қарай дамуына және басқа проблемаларды қарастыру, осы арнайы курстың мақсатына жатады.
Беріктілік қатты денелердің негізгі қасиеттерінің бірі болып есептеледі. Беріктілік сыртқы жүктелген механикалық жүкке төзімділігін сипаттайтын шама.
Беріктілік физикасының дамуын бірнеше этапқа бөлуге болады. Бірінші, негізгі даму этабы, денелерді серпінді не болмаса тұтқыр серпімді біртұтас орта деп қарастырудан, денелер атом - малекулалық жүйе деп қарастыруға өтуі жатады. Қатты денелерді бір - бірімен белгілі күшпен байланысқан атомдардан құралған деген көзқарас, денеге жүк жүктелген кездегі құбылысты таза механикалық түрде қарастыру, яғни жүктелген жүк денедегі барлық атомдар арасындағы байланыс күш шамасының қатынасына байланысты. Егер әсер етуші күш, атомдар арсындағы байланыс күшпен аз шамада болса, денеде тек серпімді деформация ғана болады. Егер тең не болмаса көп болса дене қирайды не болмаса қайтымсыз деформацияланады. Қатты дененің механикалық күш әсеріне реакциясының шамасын анықтау мақсатында дененің серпінді шегі, ағу шегі және беріктілік шегі деген шамалар енгізілеген. Осы шамалардың енгізілуі атомдар жүйесімен жүктелген сыртқы әсерлесу таза механикалық әсерлесудің айғағы деп айтуға болады. Сол себепті атомдар жүйесінің жүктелуіне байланысты тепе- теңсіздікке өтуі критикалық түрде һөтуін көрсетеді.
Бірақ көптеген жинақталған эксперименталды мәліметтерге қарағанда ендірілген шектер шамасы тұрақты емес, олар өлшеу жүргізу талаптарына байланысты . Бұл, әсіресе, қатты денелердің механикалық қасиеттерін кең аралықта денені жүктеу жылдамдығы, сынау температурасы өзгергенде периодикалық және вибрациялық жүктеулерде және т. б. жағдайларда анық байқалады.
«Шектердің» тұрақсыздығы, қабылданған механикалық модельдің (жүктелген жүктеменің атом байланыстарын бірдей кернейтін) толық еместігі «шектердің» тұрақсыздығын түсіндіретін жалпы бір физикалық құбылыстар бар екендігін байқатады. Ол физикалық құбылыс атомдардың жылулық қозғалысымен байланысты. Бірақ қатты денелердің беріктілігін зерттеуде, зерттеушілер көп уақытқа дейін атомдардың жылулық қозғалысын ескерией, атом - малекулалық қирау концепциясын құрған. Атомның жылулық қозғалысын ескерсек, атом кинетикалық қирау концепсиясы болар еді. Шынында да сыртқы жүктелген күш статикалық жүйемен әсерлеспей жылулық тербелісте қозғалатын бөлшек жүйесімен әсерлесуі керек деп қарастыруға болады. Сол тербелістің арасында атомдар байланысын кернейтін шама локальді жиі өзгеріп отырады. Локальді кернейтін шаманың өзгеруіне аса маңызды рол атқаратын атом жылулық қозғалысының біртексіздігі, яғнм энергетикалық флуктуация. Бұл атом аралықтағы жылулық флуктуация механикалық құбылыстың сипатын қатты өзгертеді, сонымен бірге механикалық процестің энергетикасын және оның денелердің басақа қасиеттерімен байланысын өзгертеді.
Атомдардың жылу қозғалысын ескеріп, денелердің физика - механикалық проблемаларын қарастыру негізіне молекула - кинетикалық концепция жатады. Жалпы бұл концепсияны кинетикалық деп атайды.
Бұл қатты денелер беріктілігінің физикалық табиғатын кинетикалық бағытта зерттеуге эксперименттік және теориялық зерттеулер өткен ғасырда негізі қаланған. Сол Я. И. Френкельдің 1930 жылдары сұйықтар мен қатты денелерде атомдардың жылулық қозғалысы теориясы болып есептеледі. Бұл теория сол кезде ақ конденсирланған ортаның көптеген кинетикалық қасиеттерін сипаттауға мүмкіндік тудырған. Атап айтұанда тұтқырлық, ағу, дифузия, булану т. б. бірақ жылулық қозғалыс теориясының физикалық табиғатын және қатты денелердің қирау механизмдерін анықтауға көпке дейін қолданбай., дененің беріктілігін зерттеу механикалық бағытта жалғастырылып дами берген. Қатты денелер қирау табиғатын кинетикалық бағытта зерттеу тек 1950 жылдары басталған. Ол академик С. Н. Журков басшылығымен бұрынғы Ленинградтың, қазіргі Санкт - Петербург қаласындағы А. Ф. Иоффе атындағы физика техникалық институтында басталған. Бұл зерттеулер механикалық қирау құбылысына және қатты денелер беріктілік табиғатына деген бұрынғы көзқарастарды толығымен өзгертті. Бұл зерттеулер денелердің атомарлық байланысынденеге жүктелген күш үзбейтіндігін, ол тек жылулық флуктуацияның үзуіне мүмкіндік тудыратынын дәлелдеді. Сонымен денелердің қирау процес екендігі анықталды. Яғни «беріктілік шегі» деген түсінікті қирау процесінде қолдануға болмайтындығын көрсетті. Осымен денелердің қирау кинетикалық теориясы толығымен жетілді деп айтуға болмайды. әлі де көптеген анықталмаған және дикуссиялы мәселелер көп. Олар беріктілік физикасының ары қарай даму жолдарын анықтайды және келешектегі қирау кинетикалық концепсиясын береді.
Берікілік проблемаларды шешуде статикалық және кинетикалық
көзқарастар.
Көп уақытқа дейін қатты денелердің беріктілік физикасының табиғатын олардың критикалық қирау түсінігімен қарастырып келгенін айтып өттік. Осы көзқараспен ақауы жоқ идеал дененің морт қирауын қарастырайық. Бұл денеге жүктелген жүк сол дененің теориялық беріктілігіне жеткенде, ол дене бірденен атомдарға шашылып кеткен болар еді. Реал жағдайда денелер бірнеше бөлікке ғана бөлінетінін және жүктелген жүк шамасы теориялық беріктілікке жетпей қирайтыны белгілі (Гриффите теориясы) . Бұл теорияның рас екендігін А. Ф. Иоффе юінің экспериментінде дәлелдеген (NaCl кристалын су ертінді ортасындағы беріктілігі теориялық беріктілікке жақын болатыны байқалған) . Бірақ Гриффите мен Иоффенің теориясы реал беріктілігінің шамасы теориялық беріктілік шамасынан төмен екендігін және денелер қирау барысында 2-3 бөлікке ғана бөлінетінін түсіндіргенімен, жүктелген жүктің әсер етуші уақыт мерзімі сол, жүктелген дененің беріктілік шамасына әсерін тигізуін түсіндіре алмайды. Мысалы, егер үлгі аз уақыт арасында жүктеліп, оның беріктілік шегі сол денеден жасалған үлгіні көп уақыт аралығында жүктелгендегі беріктілік шегіне қарағанда әлдеқайда жоғары екендігі байқалған. Бұл материаелдың статикалық шаршауы деп аталады.
Денелердің статикалық шаршауын көптеген зерттеушілер силикат шыныларда, полимерлерде, металдарда, ионды кристалдарда т. б. материалдарда байқаған.
Материал беріктілігіне жүктеу уақытының әсерін, әр түрлі жылдамдықпен жүктегенде немесе деформациялағанда беріктіліктің шегі өзгеруінен, жылжығыштық тәсілі және ұзақ мерзімді беріктілігін анықтау барысында байқауға болады.
Уақыт мерзімінің дене беріктілігіне әсерін дененің критикалық қирау сипаттамасымен біріктіруге болмайды. Шынында да бір жағынан денеге жүктелген жүк белгілі шегіне жеткенде ғана қирайтын болса, екінші жағынан сол дененің беріктілік шегінің денені жүктеу мерзіміне (уақытына) тәуелділігі бір-біріне қайшы. Бұл қайшылықка көптеген зерттеушілер көңіл аударғанымен, оны түсіндіру барысында статикалық көзқараста қалып қоя берген. Яғни, дене беріктілік проблемаларының шешімі болмаған. Мысалы, шыны материалдары беріктілігінің уақытқа тәуелділігін, Ораван Гриффитстің теориясын қолдана отырып, ауадан ылғалды copy арқасында беттік керілу коэфицентінің төмендеуімен түсіндірген:
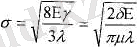
мұндағы Е - Юнг модулі, jlx - Пуассон коәффициенті X - сызат ұзындығы, у, 5 -беттік керілу (5 <1)
Ораван теориясы бойынша, үлгі тез мерзімде жүктелсе, жаңа пайда болған сызат ылғалды сорып алуға үлгермейді, сызатта беттік керілу болмайды, сондықтан да беріктілік жоғары. Ал үлгі көп уақыт мерзімде жүктелген болса, жаңа сызат ылғалды сорып алуға үлгереді, беттік кернеу сына (клин) ретінде әсерін тигізіп беріктілік шамасынтөмендетеді.
Маргетройд шыны беріктілігіне жүктеу мерзімінің әсерін, шыны екі фазадан тү_руымен байланысты деп түсіндірген. Шыны гетерогенді жүйеден түрады деп есептеп (квазитұгқырлы және серпінді әлементтерден тұрады), уақыт мерзімі еткен сайын тұгқырлы пластиктив микробелшектерде релаксация етуі нәтижесінде серпінді әлементівде кернеулік әсіп отырады. Бұл процесс серпінді әлементіндегі кернеулік материалдың беріктілік шегіне жеткенше өседі де, материал қирайды, яғни материалдың беріктілігіне уақыт мерзімінің әсерін материалдың ішіндегі кернеуліктің таралу процесімен (релаксация) байланыстырылады. Бұл гипотезаны кейбір зерттеушілер, материал беріктілік шамасының уақыт мерзіміне тәуелділігін осы күнге дейін осылай түсіндіреді. Мысалы, поликристаллы металдар үшін, әр түрлі физика-химиялық касиеттері бар материалдарда олардың беріктілігіне уақыт мерзімі әсерін тигізетіңдігі Ораванның теориясы орынсыз екендігін дәлелдейді. Мысалы, резина, пластмасса, фарфор, металдар, ионды кристалдар т. б. материалдар зерттелген. Олардың қирауына және беріктілігіне орта әр түрлі әсер өтетіндігі бізге белгілі.
Сонымен, материалдың беріктілігі уақыт мерзіміне тәуелділігіне зерттеу жүргізу, ортаға байланысты емес екендігі анықталды. Оған қосымша дәлел, кейінгі кездегі вакуумда және инертті ортада жүргізген зерттеулер беріктіліктің уақыт мерзіміне тәуелділігін көрсетеді.
Ораван мен Маргетройдтың теориясы әр түрлі болғанымен, екі теория да әрбір материалдың беріктілік шегі барлығына қарсы емес. Яғни, беріктіліктің статикалық концепциясы сақталады, материалдың қирауы критикалық түрде өтеді деп есептеді. Беріктіліктің уақыт мерзіміне тәуелділігін сыртқы қосымша процестермен байланыстырады. Алдағы қарастырылатын фенаменалогиялық және жүктелген денедегі өтетін элементар процестерді зерттеу нәтижесінде дене беріктілігінің уақыт мерзіміне тәуелділігі сыртқы қосымша процестермен байланысты болмай, беріктіліктің уақытқа тәуелділігі тікелей дененің қирау механизмімен байланысты екендігін дәлелдеді.
Сонымен, беріктіліктің уақытқа тәуелділігі, қатты денелердің қирау
заңдылығы, жалпы физикалық табиғаты бар және сол табиғатпен тікелей
байланыстылығын көрсетеді. Дене беріктілік проблемасына кинетикалық кезқараспен қарау, дене қирауы уақытқа байланысты дене ішінде қирау процесі жүріп, олардың жинақталуымен байланыстыру қажет. Олай болса, бұл процестерді анықтаудың ең оңай жолы қатты денелердің жарамдылық мерзімін тұрақты температурада және тұрақты кернеуде анықтау. Яғни, дене жүкгелген уақыттан бастап, сол дененің сол жүктің астында қирау ушін кеткен уақытты анықтау болып табылады. Материалдың механикалық беріктілігін анықтауда, кинетикалық қирау концепциясы бойынша материалдың жарамдылық мерзімі фундаментальді шама болып есептеледі. Бұл шаманы қирау процесінде орташа қирау жылдамдығына кері пропорционал деп алуға болады:
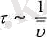
Әрбір материалдың беріктілік қасиетін және олардың қирау табиғатын кинетикалық көзқараспен анықтау үшін, ол материалдың жарамдылық мерзімінің жүктелген кернеулікке және үлгіні сынау температурасына тәуелділігін анықтау қажет: т(а, Т) -?
І тарау Әдебиеттерге шолу.
1. 1 Қатты дененің ішкі құрылымы
Қатты денелердің ішкі құрылымын сипаттау үшін кеңістік немесе кристалл торы деген түсінікті енгізу ыңғайлы.
Кристалл торы кеңістік торын құрайды, тордың түйінінде бөлшектер (атом, молекула) орналасқан болады, сонымен қатты денені құрайды
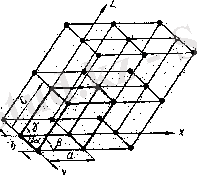
1. 1. -сурет
Қалың сызықпен ең кіші параллелепипед көрсетілген, бұл параллелепипедтің өзінің үш осі бойынша орын ауыстыруымен барлық кристалды құруға болады. Бұл параллелепипедті элементар немесе негізгі тор ұяшығы деп атайды. Бұл тор ұяшығын сипаттау үшін 6 шаманы беру керек: үш қырын ( а , в , с ) және осьтер арасындағы бұрыштарын (α, β, γ) . Бұл шамаларды тор параметрлері деп атайды. Қарапайым тор түріне куб торы жатады, мұнда а = в = c және α = β = γ = 90º. Кейбір жағдайда тордың симметриясын нақты айқындау мақсатында элементар тор шыңдарында ғана орналаспай, тағы тор ұяшығының басқа нүктелерінде де орналасқан болады. Мысалы, көлем центрленген торда кеңістік диагональдардың қиылысқан нүктесінде қосымша бір бөлшек орналасқан болады (1. 2. б -сурет), жақ центрленген торларда жақ диагональдарының қиылысқан нүктелерінде қосымша бөлшектер орналасқан болады (1. 2. в -сурет), т. б. Енді түйіндерді, бағыттарды және тордың жазықтықтарын белгілеуді қарастырайық. Бұл белгілеулерді Миллер индекстері деп атайды.
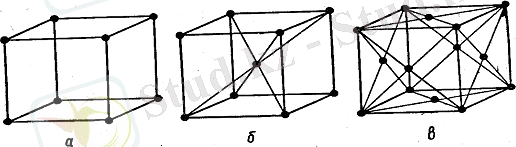
1. 2. - сурет
Тор индекстері . координата басынан алынған кез-келген тор түйінінің орнын оның x, y, z координатасымен анықтайды. (1. 3. -сурет)
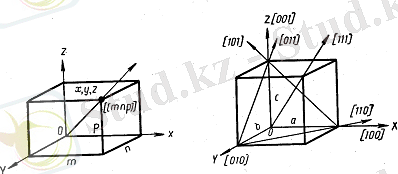
1. 3. -сурет 1. 4. -сурет
x = ma, y = nb, z = pc (1. 1)
мұндағы a, b, c - тор параметрлері, m, n, p - бүтін сандар.
Ось бойымен өлшенетін бірлікті метр деп есептемей, бірлік ретінде тордың a, b, c параметрлерін алсақ, онда тор координаталары m, n, p бүтін сандар болады. Бұл сандарды түйін индекстері деп атайды және былай жазылады: [[mnp] ] . Теріс индекс болса, теріс таңба индекс төбесіне қойылады:
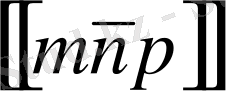 .
.
Бағыт индекстері . Кристалдағы бағытты сипаттау үшін координата басынан тура сызық алынады. Ол сызықтың орналасуын бірінші түйіннің тор индексі анықтайды, сызық сол бірінші түйіннен өтеді (1. 3. -сурет) . Сондықтан түйіннің тор индекстері бағыт индексі де болады. Бағыт индексін [mnp] - мен белгілейді. Бағыт индексінің анықтамасы бойынша, оны үш ең кіші бүтін сан анықтайды. Мысалы, координата басынан және [[345] ] түйіннен өтетін бағыт индексі [345] болады.
Мысал ретінде куб торының негізгі бағыттарын көрсетуге болады (1. 4. -сурет) . Тор осьтерінің индекстері: ОХ осінің индексі [100], ОУ осінің - [010], OZ осінің - [001] . Жақ диагональдарының индексі: вс жағы диагоналының индексі [011], ас жағы диагоналының - [101], ав жағы диагоналының - [110], кеңістік диагоналының индексі - [111] .
Кристалл жақтарының индекстері . Кристалл жақтарының орнын кристалл торының осьтерін қиып өтетін А, В, С кескіндер анықтайды. Мұндай жазық теңдеуінің түрі мынадай болады:
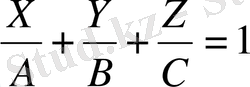 (1. 2)
(1. 2)
Мұндағы X, Y, Z - осы жазықта жататын нүктенің координаталары. Егер кристалл жазығы (жағы) тор түйінінен өтетін болса (тек сондай жақтар қарастырылады), онда жазықта жататын кез-келген түйіннің координаталары түйін индекстеріне тең:
x = m , y = n , z = p .
Сондықтан жазық теңдеуін мынадай түрде жазамыз:
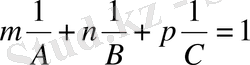 (1. 3)
(1. 3)
m, n, p бүтін сан болғандықтан, (1. 3) теңдеу 1/А, 1/В, 1/С қатынастар рационалды сандар болуы керек, олардың қатынастарын h, k, l үш бүтін сан қатынастарымен ауыстыруға болады:
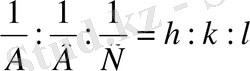 (1. 4)
(1. 4)
Осы h, k, l сандар кристалл жазықтарының индекстерін береді, олар былай белгіленеді: ( hkl ) . Жазық индекстерін былай анықтайды: тор осьтеріндегі жазықты қиып өтетін ось бірлігімен алынған А, В, С кескіндерді сол кескіндердің кері мәндеріне сәйкес, яғни 1/А, 1/В, 1/С етіп жазады. Алынған 1/А, 1/В, 1/С бөлшектерге ортақ бөлім табады. Ортақ бөлім Д болсын дейік, онда бірінші бөлшекке Д/А, екіншіге Д/В, үшіншіге Д/С болады. Д/А, Д/В, Д/С бүтін сандар кристалл жазығының h, k, l индекстері болады, яғни
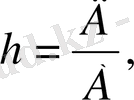
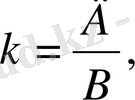
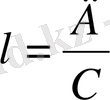 (1. 5)
(1. 5)
Мысалы: 1. Тор осьтерін қиып өтетін A=1, B=2 және C=3 кескіндерге сәйкес кристалл жазықтығының индексін анықтайық.
Шешім:
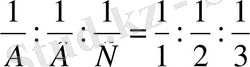 - рационал сандар, онда жалпы бөлгіш 6 болады. Олай болса,
- рационал сандар, онда жалпы бөлгіш 6 болады. Олай болса,
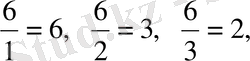 яғни h=6, k=3, l=2, жазық индексі (632) болады екен. 2. Тор осьтерін қиып өтетін A=1/2, B=2 және C=1/3 кескіндерге сәйкес кристалл жазығының индексін анықтайық.
яғни h=6, k=3, l=2, жазық индексі (632) болады екен. 2. Тор осьтерін қиып өтетін A=1/2, B=2 және C=1/3 кескіндерге сәйкес кристалл жазығының индексін анықтайық.
Шешім:
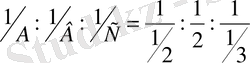 -рационалды сандар. Ортақ бөлім 2 болады, онда
-рационалды сандар. Ортақ бөлім 2 болады, онда
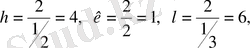 жазық индексі (416) .
жазық индексі (416) .
(1. 5) қатынастан тор осінен өтетін кескінді сол жазықтың индексімен анықтауға болатыны көрініп тұр, яғни
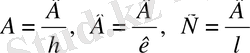 (1. 6) Сондықтан жазық индексі (
hkl
) арқылы тор осьтерін қиып өтетін кескіндерді анықтау үшін индекстердің кері мәнін жазып, яғни
(1. 6) Сондықтан жазық индексі (
hkl
) арқылы тор осьтерін қиып өтетін кескіндерді анықтау үшін индекстердің кері мәнін жазып, яғни
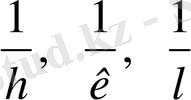 , олардың ортақ бөлімін (
Д
) анықтайды. Онда (1. 6) теңдеулер арқылы кескіндер анықталады:
, олардың ортақ бөлімін (
Д
) анықтайды. Онда (1. 6) теңдеулер арқылы кескіндер анықталады:
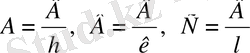
3. Тор осіндегі (123) жазықты қиып өтетін кескіндерді анықтайық.
Шешім: Жазық индексінің кері мәнін жазамыз: 1/1, ½, 1/3. Онда кескінде
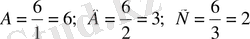 тең. Координат осьтеріне параллель жазыққа сәйкес индекс нольге тең. Мысалы (110) жазық ОZ оське параллель (011) жазық параллель ОХ осіне, т. б.
тең. Координат осьтеріне параллель жазыққа сәйкес индекс нольге тең. Мысалы (110) жазық ОZ оське параллель (011) жазық параллель ОХ осіне, т. б.
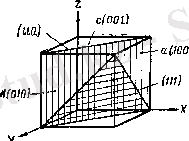
1. 5. -сурет
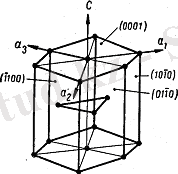
1. 6. -сурет
Мысал ретінде куб торларының негізгі жақтарының индекстерін анықтайық (1. 5. -сурет) . Куб жақтарының индекстері: «с» жақтың индексі - (001), «а» жақтың индексі - (100), «в» жақтың индексі - (010) . Жақтың диагоналынан өтетін жақтың индексі (ромбалық додекаэдр жағының индекстері: (110), (101), (011), т. б. осьтерді бірлік қимамен қиып өтетін жазықтардың (октаэдр жазықтарының) индекстері: (111), (
 ), (
), (
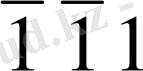 ), (
), (
 ), т. б. гексагональды кристалдардың жазықтарын белгілеу үшін 4 негізгі координата жүйесі қолданылады (1. 6. -сурет) : үш (а
1
, а
2,
а
3
) бір-біріне 120º жасаған ось, бұл осьтер алты жақты призманың бетінде жатады (базис жазықтығы), ал төртінші ось (с) базис жазықтығына перпендикуляр. Әрбір жазық 4 индекспен белгіленеді:
hkіl.
Қосымша индекс
і
үшінші орынға қойылады, бұл индекстің мәні
h
және
k
индекстер арқылы есептеледі:
і=-(h+k)
. а
1
, а
2,
а
3
осьтеріне параллель базис жазығының индексі (0001) болады. Призма бүйірінің жағына параллель жазықтың индексі мынадай типті болады: (
), т. б. гексагональды кристалдардың жазықтарын белгілеу үшін 4 негізгі координата жүйесі қолданылады (1. 6. -сурет) : үш (а
1
, а
2,
а
3
) бір-біріне 120º жасаған ось, бұл осьтер алты жақты призманың бетінде жатады (базис жазықтығы), ал төртінші ось (с) базис жазықтығына перпендикуляр. Әрбір жазық 4 индекспен белгіленеді:
hkіl.
Қосымша индекс
і
үшінші орынға қойылады, бұл индекстің мәні
h
және
k
индекстер арқылы есептеледі:
і=-(h+k)
. а
1
, а
2,
а
3
осьтеріне параллель базис жазығының индексі (0001) болады. Призма бүйірінің жағына параллель жазықтың индексі мынадай типті болады: (
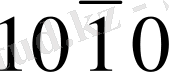 ) . Мұндай бір-біріне параллель емес беттер (жазықтар) үшеу; оларды бірінші типтегі жазықтар деп атайды.
) . Мұндай бір-біріне параллель емес беттер (жазықтар) үшеу; оларды бірінші типтегі жазықтар деп атайды.
1. 2 Моно- және поликристалды қатты денелер
Қатты денелердің бөлшектері кристал торында біртекті қатар-қатар орналасқан деп есептейік (Кристалдардағы ақауларды ескермейміз) .
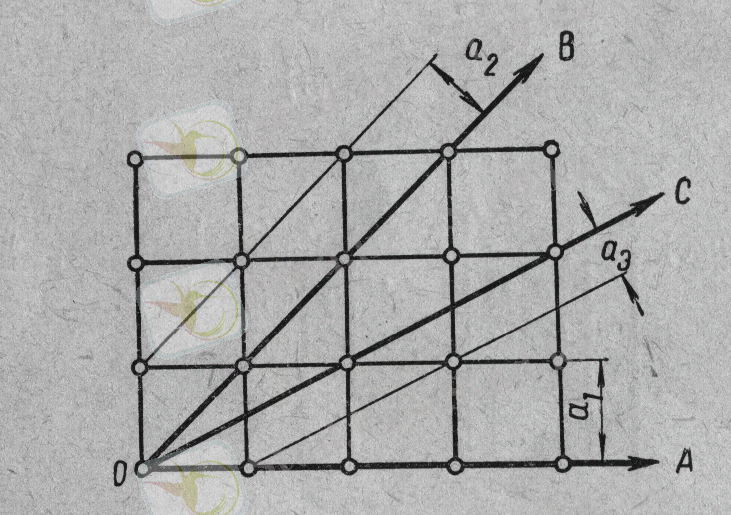
1. 7. -сурет
О нүктесінен ОА, ОВ, ОС, т. б. бағытта сызық өткізейік. Әрбір бағытта бірлік арақашықтықта кездесетін бөлшектер саны әртүрлі жиі кездесетін бөлшектер ОА бағытта, ал сирек кездесетін бөлшектер ОС бағытта. Әрбір бағыттағы қатты денелердің қасиеттерін бөлшектердің сол бағытта қаншалықты тығыз орналасуы анықтайтын болғандықтан, алынған бағыт бойынша қатты денелердің қасиеттері әр түрлі болуы керек. Дене қасиетінің бағытқа тәуелділігін (қасиеттің бағыттылығын) анизотропия деп атайды.
Арнайы жағдайда қатты денелерді бір кристалл түрінде өсіруге болады, яғни монокристалл түрінде. Бірақ көп жағдайда ерітінділерде (балқыған денелерде) бір мезгілде көптеген кристаллизацияланатын орталықтар пайда болып, көптеген өзінше бөлек кристалдар болуына алып келеді. Бұл кристалдардың өсуінің арқасында олар бір-біріне жақындай түседі. Сонымен көптеген бөлшектер пайда болады, яғни поликристалл. Өскен кристаллиттер (дәндер) әр түрлі формада болады, сыртқы көрінісі ішкі ретті құрамына сәйкес келмейді. Себебі олардың (дәндердің) орналасуы суытылған ерітіндіде (сұйық күйдегі затта) кристаллизация орталығы кездейсоқ орналасқан болады, өскен дәндердің өзара орналасуы да кездейсоқ болады. Сондықтан поликристалдарда олардың қасиеттері кристалл бағытына елеулі тәуелді болуы байқалмайды, яғни олар изотропты болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz