Үзіліссіз сигналдарды дискреттеу және кванттау: теориясы, қателіктері және есептеу әдістері


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 22 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . 3
- Сигналдарды үзілістеу теориясы . . . 4
1. 1Үзіліссіз сигналдарды үзілісті сигналдарға айналдыру түрлері.
1. 2Үзіліссіз сигналдарды уақыт бойынша үзілістеу және
1. 3 Үзіліссіз сигналдарды деңгейі бойынша үзілістеу
1. 4Үздіксіз сигналдарды әрі уақыт бойынша, әрі деңгейі
бойынша үзілістеу.
1. 5 Икемді үзілістеу (адаптивная дискретизация) .
1. 6 Үзілістелген сигналдар мәндерінің есептеу жүйелері.
1. 7 Сигналдарды үзілістеу және қайта қалпына келтірудегі қателіктер.
- Есептеулер жүргізу . . . 15
2. 1 Котельников теоремасы бойынша есептеу қадамын анықтау.
2. 2 Сигналды есептеп график құру
2. 3 Қателікті есептеу тәртібі
- Pascal тілінде есептеулер жүргізу . . . 20
3. 1 Алгоритм блок-сұлбасын құру
3. 2 Pascal тілінде программа құру
Қорытынды . . . 23
Әдебиеттер тізімі . . . 24
КІРІСПЕ
Материялдық жүйенің жағдайы туралы немесе болған бір оқиға туралы берілетін хабардың жиынтығын информация деп атайды. Осындай хабарларды тиісті орнына жеткізіп беру үшін әртүрлі жылдамдықпен таратылатын физикалық процестерді пайдалану қажет болады.
Уақытқа байланысты өзгеріп, хабарды бейнелеп бере алатын физикалық шаманы сигнал деп атайды (мысалы, ток күші, кернеу, электромагнит өрісі, т. б. ) . Хабарларды шығарып, оны түрлендіріп жөнелтуші және оны қабылдап алушы адам немесе әртүрлі таратушы, тіркеуші, сақтаушы және пайдаланушы аспаптар болулары мүмкін.
Хабар шығу көзі, хабарды сигналға айналдырып таратушы құрылғы, екі жердегі (әртүрлі қашықтықтағы) құрылғылар арасын жалғастырушы жол (орталық), сигналды қабылдап алып оны хабарға айналдырушы құрылғы және хабарды қабылдап пайдаланушы байланыс жүйесін құрады.
Информация түріне байланысты сигналдар үзіліссіз (аналогты) және үзілісті (дискретті) болып бөлінеді. Үзіліссіз сигнал бойында барлық уақытта тұрақты түрде хабар болады. Мұндай сигнал уақыт бойынша және денгейі бойынша да үзіліссіз болады. Кейбір уақытта сигнал тек қана уақыт бойынша немесе тек деңгейі бойынша ғана үзіліссіз болуы мүмкін. Үзілісті сигналдардың бойлық мәндері тек белгілі санды мәндерде ғана болады. Сондықтан үзіліссіз сигналдан үзілісті сигналға өткенде оның мәнін жуықтатып алуға тура келеді, яғни сол уақытта сигналдың тура бойлық мәнінің орнына соған жуық келетін белгілі бір мәнін алады. Сигналдың мұндай қасиетін үзіліс деңгейі деп атайды. Егер сигналда хабарлар тек белгілі бір уақытта ғана болатын болса, ондай сигналды уақыт бойынша үзілісті сигналдар деп атайды. Іс жүзінде сигналдың екі түрі де кездеседі. Мысалы, дыбыстық хабар, музыка, бейнелік, теледидар хабарлары тікелей үзіліссіз сигналдарға айналдырып, үзіліссіз (аналогтық) хабар тарату жүйесімен пайдаланады. Әртүрлі телеграф белгілері үзілісті (дискретті) хабар тарату жүйесін пайдаланады. Сигналдарды бір түрден (мысалы, үзіліссіз сигнал) екінші түрге (үзілісті) өзгертуге болады. Ол белгілі бір заңдылықпен орындалады. Кейінгі кезде үзілісті сигналдар көбірек пайдаланып, үзіліссіз сигналдардың өздерінде үзілісті сигналдарға айналдырып беру орын алады. Оның себебі үзілісті сигналдардың, үзіліссіз сигналдармен салыстырғанда біраз жетістіктерінде болып отыр: үзілісті сигналдар сандық мәнге айналдырылып қарапайым қисандық тәсілдерімен түрлендіруге ыңғайлы; үзілісті сигналдар бөгеуліктерге төзімді; үзілісті сигналдарды қайта жаңғыртқанда одан бұрынғы бөгеулік әсерлері жойылады; хабарларды сан мәнімен беру барлық хабарларға да қолданылады.
Осы курстық жұмыста үзіліссіз сигналды үзілісті сигналға айналдыру әдісі және ондағы кездесетін қиындықтар мен қателіктерді сараптап талдау қаралады. Есептеу екі (жазбаша және ЭЕМ пайдалану) түрінде жүргізіліп, кесте, графиктермен қатар есептеу машинасы бастырмасы да беріледі.
- Сигналдарды үзілістеу теориясы
1. 1Үзіліссіз сигналдарды үзілісті сигналдарға айналдыру түрлері.
Көбінесе сигнал үзіліссіз өзгеріп тұратын ток немесе кернеу күйінде кездеседі. Кейде сигнал импульс түрінде де болуы мүмкін. Информацияның кәзіргі даму кезеңіне қарай көбінесе импульс түрінде қолданылуы қолайлырақ болғандықтан үзіліссіз сигналдарды үзік (дискретті) сигналдарға ауыстырады.
Яғни үзіліссіз сигналдың орнына оның бөлек-бөлек уақыттағы мәнін алады, немесе сигнал деңгейінің әрбір деңгейлік дәрежедегі мәнін алады. Соларға қарай оны уақыт бойынша үзілістеу (дискреттеу), немесе деңгейлік дәрежесіне қарай үзілістеу дейді. Сигналдарды үзілістеудің бірқалыпты өзгеруіне орай оларды кванттау деп де атайды. Сөйтіп үзіліссіз сигналды үзілісті сигналдарға айналдырғанда, олар уақыт бойынша үзілістеу (кванттау), деңгейіне қарап үзілістеу және әрі уақыт бойынша, әрі деңгейіне қарай үзілістеу болып бөлінеді.
1. 2Үзіліссіз сигналдарды уақыт бойынша үзілістеу және
Котельников теоремасы.
Үзіліссіз сигналды үзілісті сигналға айналдырғанда үзіліссіз сигналдың мәнін тек берілген бөлек-бөлек уақыттарда ғана есептейді. Соның нәтижесінде аргумент t бойынша үздіксіз функция S(t) өзінің алғашқы үзіліссіз мәнін берілген дәлдікпен қайтадан қалпына келтіруге болады. Қайтадан қалпына келтіруші функцияны Y(T) деп белгілеп, оны кейбір функциялар f(t-t k ) қатарының қосындысы деп қарауға болады:
∞
Y(t) = ∑ ai [S(tk) S(tk-1) ] f1(t-tk), (1)
I=0
мұнда аі - коэффициенттері есептеу мүшелеріне S(t к ), S(t к -1) байланысты болады.
Сигналды үзілістегенде үзілістеу жиілігін анықтаудың яғни үзілістеу қадамының ұзындығын белгілеудің мәні зор. Егер үзіліссіз сигналдың мәнін Гк және ік-і уақыттарында жинаса үзілістеу қадамы:
Δt = t к - t к -1 (2)
Егер Δt үзілістеу қадамын өте қысқа қылып алса, онда есептелетін сан жинағы көп болып, оны қайта қалпына келтіру дәлдігі жоғары болады. Егерде Δt ұзақ болса, онда есептелетін сан жинақтары аз болып, оны қайта қалпына келтіру дәлдігі төмендейді. Әдетте, алдымен рұқсат етілетін қателік беріліп соған орай басқа амалдар анықталады. Бұндағы мақсат - ең тиімді рұқсат етілген қателіктен аспай есептелетін сан жинақтарын мейлінше азайту. Осылай болғанда барлық есепке алынатын мәндер, сигналды қайта қалпына келтіруде белгілі үлес қосады. Ал егер үзілістеудің тиімді түрін алмаса, онда маңызды мәндерден басқа басы артық мәндерде болады. Басы артық мәндерді беру үшін каналдарға қосымша уақыт немесе қосымша жылдамдық керек болады.
Әрине, былайынша жай тұрғыдан қарағанда Δt 0 болған сайын үзіліссіз функцияны қайта қалпына келтіру дәлдігі арта түседі. Бірақ та, жеткілікті дәлдікті кванттау қадамы нөлге тең болмай-ақ алуға болады. Мұндай жағдай жиілік спектрі шектелген сигналдарда болады. Сигналдар әр кезде уақыт бойынша шектеледі. Өйткені сигнал шексіз уақытта мәнгі болуы мүмкін емес. Оның басталатын және аяқталатын уақыты болады. Ал уақыт бойынша шектелген сигнал жиілік бойынша шектелмейді. Егер сигнал белгілі уақытта басталып, белгілі уақытта бітсе, оның жиілік спектрі шексіз болады. Бірақ та, барлық тәжірибеде кездесетін үзіліссіз сигналдардың қуатының негізгі бөлігі (мысалы 99%) орналасқан жиілік спектрімен шектелуге болады. Жиілік спектрінің осындай бөлігінде сигналға айналдырылған хабар туралы информацияның негізгі информациясы болады деп есептейді.
Егерде сигналдың спектрінің одан қалған бөлігін бермесе де, ол сигналды қайта қалпына келтіру дәлдігіне көрнекті әсер етпейді. Жиілігі шектелген мұндай сигнал, шындығын айтқанда, уақыт бойынша шектелмеген сигнал болады, бірақ берілген Т ұзақтығынан тысқары оның мәнін ескеруге алынбайтындай аз деп алуға болады.
Осы айтылған ойға қарай іс жүзінде кездесетін үздіксіз хабарлар мен сигналдарды жиілік спектрі шектелген функция ретінде қарауға болады.
Инженерлік тәжірибеде сигналдарды спектрі шектелген функция деп қарап, соған орай жобаланатын аспап құралдарды өткізу жолағын анықтайды. Мысалы, телеграфтың каналдық жиілік спектрінің кеңдігі, одан өтетін сигнал жылдамдығына байланысты бірнеше жүздеген Гц; телефон каналы - 3. 4 кГц, хабар тарату каналы- 8-10 кГц, теледидар каналы - 6-1 0 мГц т. с. с.
Осы айтқандарға сүйене отырып, байланыс техникасында 1938 жылы академик Котельников В. А. тұжырымдаған теореманы пайдалануға болады.
Котельников теоремасы. Егер S(t) үзіліссіз функциясы Дирихле шартын қанағаттандыратын болса (шектелген, бөлек-бөлек үздіксіз, шындық мәндерінің саны белгілі) және оның спектрі берілген ω жиілігімен шектелген болса, онда есептеу мәндерінің ең ұзын t: аралығы анықталып және осы аралықпен үзілістелген функцияны қатесіз қайтадан қалпына келтіруге болады. Осы ең ұзақ аралық:
1 (3)
2F
мұнда Ғ - ең жоғары жиілік шегі (егер сигнал спектрі нөлден басталса) .
Осы теореманы дәлелдеу үшін үзіліссіз функцияның S(t) тура және кері Фурье түрлендірулерін қарайық:

 S(jω) = ∫S(t) е
-jωt
dt, (4)
S(jω) = ∫S(t) е
-jωt
dt, (4)

 ∫S(jω) е
jωt
dω, (5)
∫S(jω) е
jωt
dω, (5)
Функция спектрі і жиілігімен шектелген дейік:
S(jω) ≠ 0, -ω F ≤ ω≤ω F ;
S(jω) = 0, │ω│>ω F ; (6)
Сонда (5) теңдігіндегі интегралдау шегін -ω F және ω F деп алса,
S(t) = ∫S(jω) е jωt dω, (7)
мұны комплексті Фурье қатарымен жазса
∞ jπ(kω/ ωF)
S(jω) = Σ Ak e (8)
k=-∞
мұнда
1 ωF - jπ(kω/ωF)
Ak = ∫ S(jω) e dω (9)
2ωF -ωF
(7) мен (9) формулаларын салыстырғанда, егер t=-kΔt деп алынса, олар тұрақты көбейткіш Δt=π/ω, дәлдігімен бірдей болады. Сондықтан осы теңдікті (8) формуласына қойса
∞ jπkω/ωF
S(jω) = Σ (π/ωF) S(-kΔt) e (10)
k=-∞
ал (10) формуласын (7) формуласына қойса, қосындылау оң және теріс таңбалы К арқылы болатындықтан К-ның таңбасын өзгертіп және интеграл мен қатардың қасиеттерін ескере отырып интегралдау мен қосындылау тәртібін ауыстырып жазамыз
1 ωF jωt ∞ jπkω/ωF
S(t) = ∫ e dω Σ (π/ωF) S(-kΔt) e =
2π -ωF k=-∞
1 ∞ ωF jω(t-kΔt)
= ∑ S(kΔt) ∫ e dω, (11)
2πωF k=-∞ -ωF
осыны интегралдағаннан кейін
ωF jω(t-kΔt) 1 jω(t-kΔt) ωF 2sin ωF(t-kΔt)
∫ e dω = e │=-,
-ωF j(t-kΔt) -ωF ωF(t-kΔt)
(11) теңдігіне қойып,
∞ sin ωF(t-kΔt)
S(t) = ∑ S(kΔt) , (12)
k=-∞ ωF(t-kΔt)
аламыз, мұнда S(kΔt) - үздіксіз функцияның әрбір жеке нүктелік орындарындағы t=kΔt есептелінетін мәні.
Сөйтіп үздіксіз функция өзінің есептік функция деп алынатын мәндерінің қатарына таралып жазылады:
sin ωF(t-kΔt)
Yk(t) = (13)
ωF(t-kΔ)
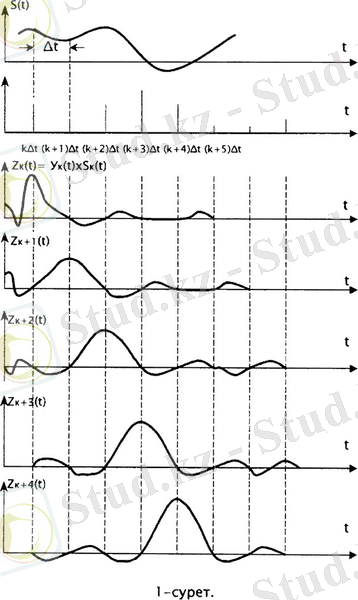 Котельников теоремасының сызықтау көрсетілуі 1-суретінде берілген. Бұл суретте көрсетілген үзіліссіз S(t) функциясы өзінің есептелінетін к∆t - нүктелерінде тек қана бір құрастырушыдан құралып, ал басқа нүктелердегі есептелінетін функциялар тап осы жерде нөлге тең болады. Есептелінетін нүктелердің аралықтарындағы барлық функцияларда үлес қосады.
Котельников теоремасының сызықтау көрсетілуі 1-суретінде берілген. Бұл суретте көрсетілген үзіліссіз S(t) функциясы өзінің есептелінетін к∆t - нүктелерінде тек қана бір құрастырушыдан құралып, ал басқа нүктелердегі есептелінетін функциялар тап осы жерде нөлге тең болады. Есептелінетін нүктелердің аралықтарындағы барлық функцияларда үлес қосады.
Есептік функцияның мынадай қасиеттері бар:
1) t = kΔt уақытында есептік Y(t) функциясы өзінің ең жоғарғы мәнінде 1-ге жетеді (2-сурет) ;
2) Δt=t-(k±l) уақыттарында (I-бүтін сан) есептік функция нөлге айналады;
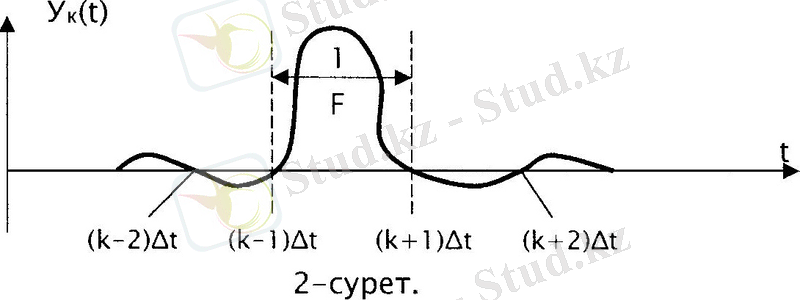 3) есептік функция өте ұзақ уақыт аралығында ортогоналды болады.
3) есептік функция өте ұзақ уақыт аралығында ортогоналды болады.
Сонымен, есептеу функциясы кірісіне импульстік функция берілген ешқандай кемістігі жоқ төменгі жиіліктегі электр сүзгісінің шығысындағы функцияны көрсетеді. Сөйтіп үзіліссіз S(t) функциясы өзінің kΔt уақыттарындағы есептелетін мәндерімен берілуі мүмкін. Оны қайтадан қалпына келтіру үшін өткізу жолағының жоғарғы жиілігі ωс электр сүзгісінің кірісіне өте жіңішке, ал амплитудасы (бойлығы) үздіксіз функцияның бойлығына тең, бірінен-бірі Δt аралығында қайталатын импульс беріледі. Сүзгінің әсер ету уақыты шектелген жиіліктегі функция тіктілігіне байланысты өседі. Ешқандай кемістігі жоқ электр сүзгісі үшін сигналдың кесілу тіктілігі үлкен болғандықтан, оның әсерінің кешіктірілуі де үлкен болады.
Котельников теоремасының ерекше мәні - оның үздіксіз хабарды зерттеудің орнына үзік-үзік хабарларды ғана зерттеумен алмастырып есепті жеңілдетуінде. Үздіксіз сигналды үзік-үзік сигналға айналдырудың тағы бір түрі Железнов Н. А. еңбектерінде кездеседі.
Есептеу нүктелерінің t аралығын анықтауды Железнов Н. А. кездейсоқ сигналдарға шешкен. Мұндай моделдегі үздіксіз сигналдың ерекше қасиеттері мынадай:
1) сигнал спектрі біртұтас және жиіліктің барлық осінде(∞<f<+∞) нөлге тең емес;
2) сигналдың ұзақтығы шектелген;
3) сигналдардың корреляциялық функциясы қаралатын Ʈ 0 аралығынан тысқары жерде нөлге тең болады;
4) сигналдың тұрақтылы да, тұрақтылы емес те кездейсоқ функциялары қаралады.
Сигналдың Т ұзақтығы Ʈ 0 корреляциялық аралықтан анағұрлым көп болуы керек: Т>> Ʈ 0 .
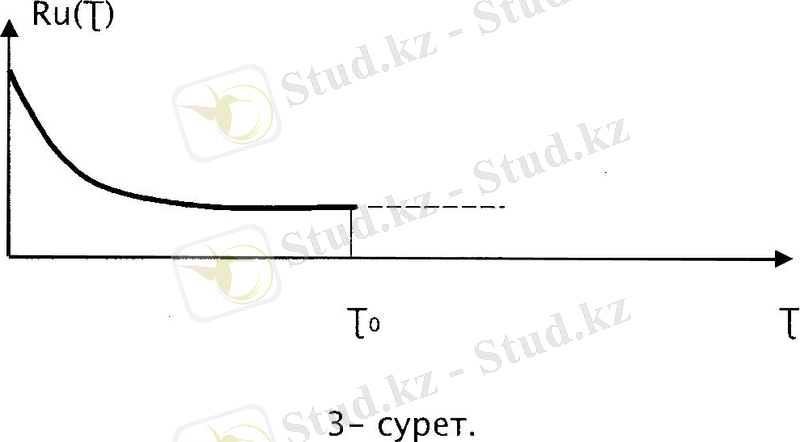 Сигналдың ұзақтығының шектілігі мен оның спектрінің шексіздігі - осы
Сигналдың ұзақтығының шектілігі мен оның спектрінің шексіздігі - осы
моделдің жетістігіне жатады. Бұл моделдің жалғыз ғана шектелетіні - корреляциялық функция (3-сурет) .
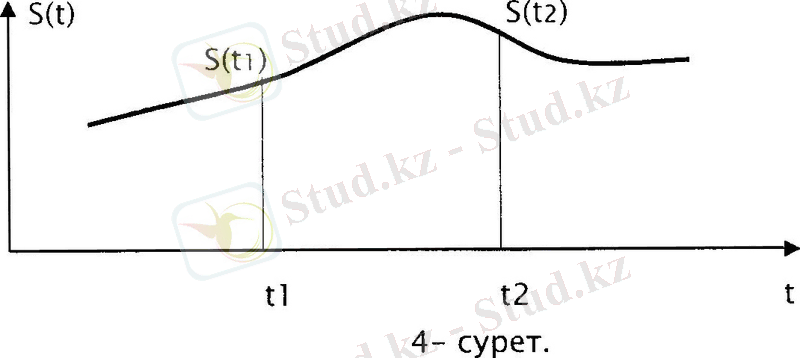
Яғни S(t1) және S(t2) үзіліссіз функцияның (4-суретте) көршілес 1-ден артық нүктеден саналатын мәндері бір-біріне тәуелсіз деуге болады.
 Тұрақтылы кездейсоқ сигналдар үшін Н. А. Железновтың көрсетуі бойынша олар сызықтық болжамдау жүйесімен беріледі. Ал оның орташа квадрат қателігі тек қана корреляциялық аралыққа тең уақытта ғана нөлден онша көп болмайды.
Тұрақтылы кездейсоқ сигналдар үшін Н. А. Железновтың көрсетуі бойынша олар сызықтық болжамдау жүйесімен беріледі. Ал оның орташа квадрат қателігі тек қана корреляциялық аралыққа тең уақытта ғана нөлден онша көп болмайды.
Сонымен, Т ұзақтығы шектелген үздіксіз сигнал үшін (Т>>Ʈ 0 болғанда) корреляцияланбаған есептеу саны N - нен көп болмайды:
N=Т/ Ʈ 0 (14)
Сондықтан үздіксіз функцияны Ʈ 0 қадамымен үздіктеу (дискретизация), оны сызықтық болжам бойынша алынған шамасының көмегімен осы Ʈ аралығында үздіксіз функцияны қайта қалпына қатесіз келтіру мүмкіндігін береді. Белгілі сигналдарға корреляциялық аралық қаралуы қалай есептейтінін көрсетейік.
Корреляциялық аралық қадамды есептеу үшін сигналдың тиімді жиіліктік жолағы деген түсінікті кіргізейік. Сонда
1 ∞
Suu Δωэфф = ∫ Suu(ω) dω, (15)
Suu max 0
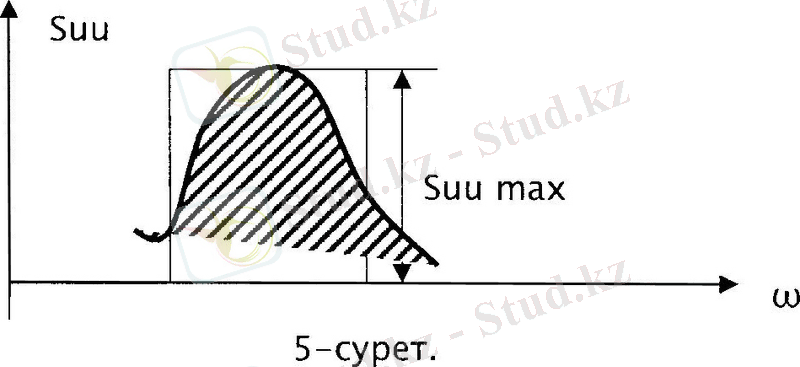 мұнда Suu max - сигналдық спектр тығыздылығының ең көп мәні; Δωэфф - сигналдың тиімді жиілік жолағы (5-сурет) .
мұнда Suu max - сигналдық спектр тығыздылығының ең көп мәні; Δωэфф - сигналдың тиімді жиілік жолағы (5-сурет) .
Железновтың үзіктеу принципі тек қана жоғарыда айтылғандай тұрақтылы кездейсоқ сигналдарға ғана емес, тұрақтылы емес кездейсоқ сигналдарға да қолданылады. Тұрақтылы емес кездейсоқ сигналдарда корреляциялық аралық Ʈ 0 (t) деген түсінік кіргізіледі.
1. 3 Үзіліссіз сигналдарды деңгейі бойынша үзілістеу
Деңгейі бойынша үзіктегенде сигналдың барлық деңгейлік ауқымы (а, b) n- бөлікке бөлінеді
ΔSi=Si-Si-1, i=1, 2, …, n; S0 = a, Sn = b.
Кез келген (S i-1 , S i ) аралығында кез келген S i мәні S i мәніне жақындатып алынады: Si = i ΔS, S i мәндері кванттау деңгейлері деп аталады (і = 1, 2, . . . , n) .
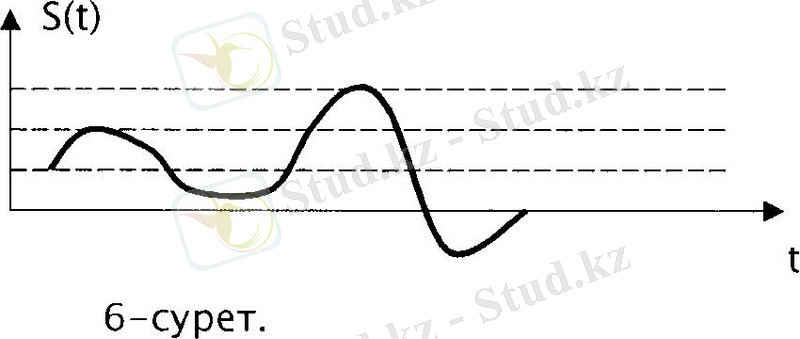 Сөйтіп деңгейі бойынша квантталғанда S(t) функциясының үзіліссіз мәні деңгейлерінің айырмашылығы ∆S үзік мәндрімен ауыстырылады. Есептеу мәндері сигнал келесі ∆S деңгейіне өзгерген уақыттарында алынады. Сондықтан импульс амплитудалары (бойлықтары) ∆S пен еселеніп саналады да, ал олардың жалпы саны S(t) функциясының өзгеруінің тіктігіне және кванттау қадамына ∆S байланысты болады (6-сурет) .
Сөйтіп деңгейі бойынша квантталғанда S(t) функциясының үзіліссіз мәні деңгейлерінің айырмашылығы ∆S үзік мәндрімен ауыстырылады. Есептеу мәндері сигнал келесі ∆S деңгейіне өзгерген уақыттарында алынады. Сондықтан импульс амплитудалары (бойлықтары) ∆S пен еселеніп саналады да, ал олардың жалпы саны S(t) функциясының өзгеруінің тіктігіне және кванттау қадамына ∆S байланысты болады (6-сурет) .
Кванттау қадамы сигнал түрлендіргіштің талдағыштық қабілетін анықтайды. Кванттау қадамы азайған сайын талдағыштық қабілеті жоғарылай түседі. Егер деңгей бойынша кванттау нәтижесі екілік кодамен берілетін болса, және оның ең кіші разряды кванттау қадамына тең болса, онда мұндай түрлендіргіштің екілік разрядының саны былай есептелген болар еді:
n= loq2N, (16)
мұнда N - үзіктеу аралығындағы кванттау қадамының саны.
Егер n берілген болса, онда кванттау қадамын табуға болады:
[S(t) ] max - [S(t) ] min
S = (17)
2ⁿ -1
Әрине кванттау қадамының шамасы шуыл деңгейінен кем болмауы керек.
1. 4Үздіксіз сигналдарды әрі уақыт бойынша, әрі деңгейі бойынша үзілістеу.
Әрі уақыт бойынша, әрі деңгейі бойынша үзілістегенде алдымен уақыт бойынша бірі-бірінен Δt аралығында орналасқан нүктелерді белгілеп, одан кейін осы уақыттағы функция мәнінің ΔS қадамына жақын тұрған деңгейін алады (7-сурет) .
1. 5 Икемді үзілістеу (адаптивная дискретизация) .
Егер осыған дейінгі қаралған әдістер сигналдардың мүмкін болатын барлық түрлеріне қарастырылып, сондықтан оның динамикалық сипаттамасының ең шеткі мәндеріне дейін арналған болса, үзілістеудің икемделген әдісінде динамикалық сиппатаманың тек кездесетін түрлерін ғана ескеріп, сондықтан қайтадан қалпына келтіруге болатын мәндерінің санын азайтуға болады. Икемді үзілістеудің негізінде, қателіктің шамасына қарай, сигнал мәнін есептеу нүктелерін белгілеу алынған.
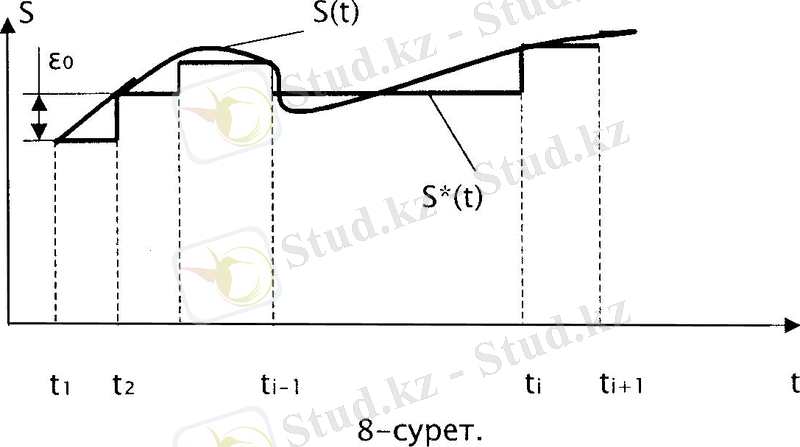 Кең таралған әдістің бірі үзіктеу тәртібін аппроксимациялау аралығының ұзақтығын икемдеу арқылы белгілеу. Есептелінетін мәнді сигналдың мәнімен аппроксимациялауды бірінің соңынан бірін жүргізгенде, сигналды S(t) есепке алынатын мәнмен S*(t) салыстырып, екеуінің айырмашылығы жіберілуге болатын қателіктен
(
ε
0
)
артық болмауы қарастырылады (8-сурет) .
Кең таралған әдістің бірі үзіктеу тәртібін аппроксимациялау аралығының ұзақтығын икемдеу арқылы белгілеу. Есептелінетін мәнді сигналдың мәнімен аппроксимациялауды бірінің соңынан бірін жүргізгенде, сигналды S(t) есепке алынатын мәнмен S*(t) салыстырып, екеуінің айырмашылығы жіберілуге болатын қателіктен
(
ε
0
)
артық болмауы қарастырылады (8-сурет) .
Сигналды қайтадан қалпына келтіру үшін , есепке алу мәндерін таңдағанда, көбінесе алгебралық полином пайдаланылады
N i
S*(t) = Σ a i t, (18)
I=0
мұнда а і - коэффициентгер.
Осы көпмүшеліктің нөлдік немесе бірінші дәрежедегілері пайдаланылады. Осыны пайдаланып 8-суретінде көрсетілген сигналды икемді үзілістеу мысалын қарайық. Алдымен нөлдік дәрежедегі мәдерін қарастырсақ, t і -уақытындағы S*(t) -мәнін S(t) -ға тең деп алады да, одан кейін ΔS(t) =S(t) -S*(t) айырмашылығын ε 0 мен салыстырады. Сөйтіп, ΔS(t) = ε 0 , ti+1 уақытында келесі есептелетін уақытқа сәйкес болады. Егер көпмүшеліктердің бірінші дәрежелерін пайдаланса, онда 9-суретте көрсетілгендей аппроксимациялау аралығнның бастапқы нүктесінде t i
S*(t) =S(t i ) + S’(t i ) t, (19)
мұнда S’(t i ) - сигналдың t i - уақытындағы туындысы. Келесі есептелетін уақытта
ΔS(t) = S(t) -S(ti) -S’(ti) t =ε₀ (20)
Берілген ε 0 шамасымен келесі есептелетін уақыт белгіленеді.
1. 6 Үзілістелген сигналдар мәндерінің есептеу жүйелері.
Үзілістелген сигнал мәндерін есептеу жүйелерінің біріне ауыстырып, одан әрі түрлендіреді. Есептеу жүйесі деп кез-келген санды көрсете алатын белгілер мен оның аталу жиынтығын айтады. Сандардың әртүрлі жазылу жүйелері бар екені белгілі (ондық, сегіздік, үштік , екілік, оналтылық ж. т. б. ) . Мұнда жүйенің негізі неғұрлым аз сан болса, онда қолданылатын сандардың түрлері аз болып, ал сандық жазылу ұзындығы көп болады. Екінші жағынан жүйенің негізі неғұрлым көп болса, онда санның жазылу ұзындығы аз болады, бірақ мұнда қолданылатын сандардың түрлері соғұрлым көп болады.
Егер әртүрлі сандық мәндер санын М-деп алса, ол 0-ден М 1 -ге дейін болып М = М 1 + 1, есептеу жүйесінің негізін b-деп белгілеп, одан разряд n- санын анықтауға болады, яғни
М = b n , одан n= ln М/ln b (21)
Егер М 1 = 999, М = 1000, b = 10 болса, онда n = ln 1000/ln 10=3. Ал егер М 1 = 1000, М = 1001 болса, S=10, n>3, яғни 4 болады.
Физикалық тұрғыдан қарағанда сандарды алмастырғанда, есептеу жүйесінің негізі неғұрлым аз болса, сигналдық физикалық әртүрлі жағдайы да соғұрлым аз болады. Сондықтан ең қолайлысы екілік жүйе болады. Бірақ, екінші жағынан қарағанда есептеу жүйесінің саны неғұрлым аз болған сайын, әр санды белгілейтін разряд соғұрлым көп болып, оны шығаратын құралдар саны да көбейе түседі. Сонымен есептеу жүйесін қалап алуда бір жағынан санның түрін азайту, екінші жағынан оны қысқаша жазуға тырысу сияқты қарама - қарсы қойылатын қайшылықты шешуге тура келеді.
Мысалы үшін есептеу жүйесінің негізін b деп алғанда, оның әрқайсысын белгілеуге керекті электронды құрылғы саны b болады, яғни бір разрядта тұратын сан түрін b триодпен беруге болады.
Сандық мәнді М деп алғанда, ондағы разрядты п деп алса, оған керекті электрондық аспап саны
N = b . n = b . (ln М/ln b), оның шыңдық (экстремалдық) мәнін М=const деп санап, dN/db туындысын 0-ге теңеп табады
dN ln b-1
= ln M =0, (22)
db (ln b) ²
кез-келген шектелген b үшін ln M/(ln b) ²≠0 болғандықтан ln b-1=0, сонда b=2. 718. Оған ең жақын келетін жүйе 3 болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz