Сырықтардың деформациясын математикалық тұрғыда ұтымды басқару моделі

Пән: Математика, Геометрия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. И. СӘТПАЕВ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ

Информациялық технологиялар институты

Математика кафедрасы

Ташигенова Акерке Омирбековна

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: «Сырықтардың деформациясын математикалық тұрғыда ұтымды басқару моделі»

050705-Математикалық және компьютерлік модельдеу

Алматы 2011

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. И. СӘТПАЕВ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ТЕХНИКАЛЫҚ УНИВЕРСИТЕТІ

Информациялық технологиялар институты

Математика кафедрасы

ҚОРҒАУҒА ЖІБЕРІЛДІ

Кафедра меңгерушісі

пед. ғыл. д-ры, профессор

О. С. Сатыбалдиев

«___»2011ж.

ДИПЛОМДЫҚ ЖҰМЫС

Тақырыбы: Сырықтардың деформациясын математикалық тұрғыда ұтымды басқару моделі

050705 Математикалық және компьютерлік модельдеу

Орындаған Ташигенова А. О.

Рецензент Ғылыми жетекшісі

Т. Рысқұлов атындағы ҚазЭУ-нің физ. -мат. ғыл. кандидаты, доцент

инж. -эк. -лық фак. директоры

А. Г. Ибраев Б. Ж. Сағындықов

« »2011ж. « » 2011ж.

Алматы 2011

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

Қ. И. Сәтбаев атындағы Қазақ ұлттық техникалық университеті

Ақпараттық технологиялар институты

Математика кафедрасы

050705 - математикалық және компьютерлік модельдеу

БЕКІТЕМІН

«Математика» кафедрасының

Меңгерушісі пед. ғыл.

докторы, профессор

О. С. Сатыбалдиев

«___» 2011 ж.

Дипломдық жұмысты орындауға

ТАПСЫРМА

Студентке Ташигенова Ақерке Өмірбекқызы

Тақырыбы: «Сырықтартардың деформациялануын математикалық тұрғыда ұтымды басқару моделі»

Университеттің бұйрығымен бекітілген № 628-n « 09 » қараша 2010ж. бастап

Жұмысты тапсыру мерзімі: «___»

Дипломдық жұмысқа бастапқы деректер: таза және көлденең иілу Лагранж көбейткіштері.

Дипломдық жобада әзірлеуге жататын сұрақтар тізбесі немесе дипломдық жұмыстың қысқаша мазмұны:

a) процесстерді басқарруды есебінің қазіргі күйінің әдеби шолуы;

б) басқару жүйесінің құрылымдық схемаларының математикалық үлгінің құрастыруы және өңдеуі;

в) басқару жүйесінің өңдеуі.

Графикалық материал тізбесі: Microsoft PowerPoint қосымшасын қолданып, презентация жасау.

Ұсынылатын негізгі әдебиеттер: a) Жүнісбеков С. Материалдық кедергісі: оқулық. / Жүнісбеков С. - Алматы: «Бастау», 2011. - 364 бет.

Дипломдық жұмысты дайындау

КЕСТЕСІ

Бөлімдердің атауы, әзірленетін сұрақтар тізбесі

Ғылыми жетекші

мен кеңесшіге

көрсету мерзімі

Ескертпелер

Бөлімдердің атауы, әзірленетін сұрақтар тізбесі: Процесстерді басқарруды есебінің қазіргі күйінің әдеби шолуы

Ғылыми жетекшімен кеңесшігекөрсету мерзімі: 24. 01. 11-19. 03. 11

Ескертпелер:

Бөлімдердің атауы, әзірленетін сұрақтар тізбесі: Басқару жүйесінің құрылымдық схемаларының математикалық үлгінің құрастыруы және өңдеуі

Ғылыми жетекшімен кеңесшігекөрсету мерзімі: 21. 03. 11 - 09. 04. 11

Ескертпелер:

Бөлімдердің атауы, әзірленетін сұрақтар тізбесі: Басқару жүйесінің өңдеуі

Ғылыми жетекшімен кеңесшігекөрсету мерзімі: 07. 02. 11 - 30. 04. 11

Ескертпелер:

Қолтаңбалары

Бөлімдердің атаулары

Ғылыми кеңесші,

аты-жөні

(ғылыми дәреже, атағы)

Қол қойған мерзімі

Қол таңбасы

Бөлімдердің атаулары: Процесстерді басқарруды есебінің қазіргі күйінің әдеби шолуы

Ғылыми кеңесші,аты-жөні(ғылыми дәреже, атағы):

ф. -м. ғ. кандидаты, доцент,

Б. Ж. Сағындықов

Қол қойған мерзімі:

Қол таңбасы:

Бөлімдердің атаулары: Басқару жүйесінің құрылымдық схемаларының математикалық үлгінің құрастыруы және өңдеуі

Бөлімдердің атаулары: Басқару жүйесінің өңдеуі

Бөлімдердің атаулары: Нормабақылаушы

Ғылыми кеңесші,аты-жөні(ғылыми дәреже, атағы):

ф. -м. ғ. кандидаты, доцент,

У. Б. Жаңбырбаева

Ғылыми жетекші Б. Ж. Сағындықов

Тапсырманы орындауға қабылдап алған студент А. Ө. Ташигенова

Күні “” 2011ж.

АНДАТПА

Бұл «Сырықтардың деформациясын математикалық тұрғыда ұтымды басқару моделі» дипломдық жұмысы механизмді ұтымды ұйымдастыру негізінде сырық деформациясын математикалық тұрғыда талдауға арналған.

Математика мен механикаға ортақ есеп негізінде консолды және айнымалы қима сырықтарының деформациясын оптимизацияда жиі қолданыс табатын Лагранж көбейткіштер және Ритц әдістері арқылы ұтымды басқару моделін құру жұмыстың басты зерттеу объектісі болып табылады.

Зерттеу барысында жалпы қатты денелердің деформация процессі қатты дененің механикасы, құрылыс механикасы, гидродинамика, геофизика ғылымдарының бөлімдерінде жақсы жетістіктерге алып келеді.

Жұмыстың маңыздылығы материалдардың жаңа моделін өңдеу, белгілі модельдер шегінде тегіс және кеңістік есебінің көптеген класын математикалық әдіспен зерттеу тиімділігі, сырық параметрлерінің әсеріне негізделген негізгі механикалық факторлардың теориялық талдауы болып табылады.

АННОТАЦИЯ

В данной дипломной работе под названием «Оптимальное управление деформированием стержней» рассмотрены задачи оптимального управления с полной обратной связью математическими методами.

На основе построенной математической модели системы управления деформированием стержней были проведены процедуры анализа устойчивости, системы управления деформации, получены результаты моделирования в виде переходных процессов системы оптимального управления стержнями. С использованием методов множителей Лагранжа и Ритца строится основа моделя управления деформированием твердых тел. Полученные алгоритмы были реализованы с использование среде Maple, с помощью которых были получены графики процессов системы оптимального управления деформированием стержней.

ABSTRACT

In this research project titled "Optimal control of the deformation of the rods" are considered optimal control problem with full feedback by mathematical methods.

Based on this mathematical model of the deformation of the control rods were performed analytical procedures stability control strain obtained simulation results in a transient system optimal control rods. With the use of Lagrange multipliers and the Ritz is constructed based on the model control the deformation of solids. Derived algorithms have been implemented with the use of environment Maple, with the help had been received timing of the process of optimal control the deformation of the rods.

МАЗМҰНЫ

Кіріспе

9-11

Кіріспе: 1. Сырықтар деформациясын ұтымды басқару есептері.

9-11: 12

Кіріспе: 1. 1. Лагранж көпмүшеліктер әдісі

9-11: 12

Кіріспе: 1. 2. Ритц әдісі

9-11: 12-13

Кіріспе: 1. 3. Деформациялануды ұтымды басқару есебінің қойылуы

9-11: 13

Кіріспе: 1. 4. Деформацияның потенциалдық энергиясы

9-11: 14-17

Кіріспе: 1. 5. Консолды сырық деформациясын басқару

9-11: 17-20

Кіріспе: 2. Материалдар кедергісінің негізгі болдамдары

9-11: 20-21

Кіріспе: 2. 1. Айнымлы қима пішімін басқару

9-11: 22

Кіріспе: 3. Ішкі күштердің эпюралары

9-11: 23-24

Кіріспе: 3. 1. Айнымалы қима сырығының деформациясын басқару

9-11: 24-26

Кіріспе: 4. Күрделі құрылымды сырық есебін модельдеу

9-11: 25

Кіріспе: 4. 1. Байламалы-серпімді материалдардың моделін Maple бағдарламасының көмегімен өңдеу.

9-11: 26-39

Кіріспе: 4. 2. Қимасы дөңгелек тік білеудің бұралуы

9-11: 39-42

Кіріспе: 4. 3. Бұралған біліктегі деформация мен орын ауыстыру

9-11: 42-43

Кіріспе: 4. 4. Бұралуда бұрыштық орын ауыстырулардың эпюрасын тұрғызу

9-11: 44

Кіріспе: 4. 5. Бұралудағы энергия

9-11: 45

Кіріспе: 4. 6. Қимасы дөңгелек емес сырықтың бұралуы

9-11: 46-47

Кіріспе: 4. 7. Жұқа қабырғалы тұйық пішімді сырықтардың бұралуы

9-11: 47-48

Кіріспе: 5. Иілу туралы жалпы түсінік

9-11: 49-53

Кіріспе: 5. 1. Көлденең иілу

9-11: 53

Кіріспе: 5. 2. Иілудегі басты кернеулер

9-11: 53-54

Кіріспе: 5. 3. Иілген арқалықтың орын ауыстыруы

9-11: 54-55

Кіріспе: 6. Деформацияны ұтымды басқару есептеріндегі неізгі ұғымдар мен амалдар

9-11: 56

Кіріспе: 6. 1. Көпайнымалы функцияны экстремумға зерттеу

9-11: 56-58

Кіріспе: 6. 2. Функционал

9-11: 58

Кіріспе: 6. 3. Сепарабельдік кеңістік

9-11: 59-61

Кіріспе: Қорытынды

9-11: 61

Кіріспе: Пайдаланылған әдебиеттер

9-11: 62

Кіріспе: Қосымша А

9-11: 63

Кіріспе: Қосымша Б

9-11: 64

КІРІСПЕ

Инновациялық технологиялардың дәуiрлеуi барысында көптеген көкейтесті шешімі табылмаған тапсырмалар пайда болуда, бұнымен бiрге және өнеркәсiп барлық салаларындағы басқару жүйелерiнiң автоматтандырылуы программалық және механикалық қамтуларды талап етуде. Бул дәуірлеу процессі өте қарқынды жылдамдықта дамып жатқандықтан барлық процесстерді, соның ішінде механизмді ұтымды ұйымдастыру маңызды мәселе болып отыр. Қандай болмасын өнеркәсiптiк немесе мамандандырылған жабдық құрылымдар тапсырмалардың жылдам шешімінсіз ешқандай даму, дәуірлеу процесін елестетуге болмайды. Сондықтан да біз осы дипломдық жобада механикадағы сырықтардың деформациялануын ұтымды басқару есептерiн Лагранж көбейткiші және Ритц әдiстерi арқылы және Maple бағдарламаларының көмегімен шешудің жолдарын көрсетеміз.

Қатты заттар деформациялануын ұтымды басқару есептерi қатты емес бөлшектердi ғарыш кеңiстiгiнде түпкi қаттылықтың манипуляторларын қолдануында, тарқату және iрi қатты емес конструкциялардың құрастыру жағдайында көкейкестi мәселе болып отыр. Бұл жұмысты баяндау барысында үш түрлі мысал келтіремін.

«Сырықтардың деформациалануын ұтымды басқару есептеріндегі Лагранж көбейткіші және Ритц әдісі» атты бірінші бөлімде теориялық және эксперименттік жоспарда деформацияланатын ортаны математика мен оптимизацияда жиі қолданылатын Лагранж теңдеуі және экстемумға зерттеу есебі арқалы деформация кезінде энергияның минималды шығынын қамтамасыз ететін әсерлерді таба отырып, деформацияны ұтымды басқару моделі құрылады.

Яғни, консолды сырықтың деформациялануын басқаруды қарастырамыз. Ол үшін Лагранж көбейткішімен біріккен Ритц әдісін қолданамыз. Және де осы есептің шешімін solve функциясының көмегімен Maple -да Лагранж көпмүшелігінің көмегінсіз есептеп шығаруға болады.

Екінші есеп айнымалы қиманың пiшімін басқаруға негізделген. Бұл есепте инерция моменті және толық энергия формулаларын Maple -дың көмегімен түрлендіреміз де оңай шешімін табамыз.

Үшінші мысалымыз айнымалы қима сырығының деформациясын басқаруға негізделген. Мұнда минимумның жеткiлiктi шарттары (квадратты форманың оң айқындығы) Гэссэ матрицасын қолданып тексерiлген.

Динамикалық деформацияланатын байламалы-серпімді материалдардың моделін Maple бағдарламасының көмегімен өңдеу атты тортінші бөлімде Maple бағдарламасының көмегімен құрылыс конструкцияларындағы қатпарлы пластинкалардың графиктері сызылып, моделдері құрылады.

Қорыта келгенде бұл жұмыста механикадағы сырықтардың деформациялануын бірнеше математикалық тәсілдер:Лагранж көпмүшеліктер және Ритц әдістерін, физикалық шамылар: инерция моменті және толық энергияны және Maple бағдарламасы арқылы математикалық тұрғыда ұтымды басқару моделін құрастырдық.

Зерттеудің көкейкестілігі. Ғылымның және техниканың дамуы, жаңа құрылыстарды құру, ғылыми-техникалық прогрессияның жоғарылау деңгейіне жауап беретін, деформацияланатын ортаның және динамика облысында зерттелетін талаптарды қадағалайтын сапалы материалдарды және технологияларды пайдалану болып табылады.

Нақты қолданбалы есептер және механикадағы деформацияланатын қатты дене зерттелуінің даму заңдылығы жарық көруде. Мұның толық есебі үшін материалдардың физика-механикалық қасиеті, уақыт бойынша олардың деформацияланатын сипаттамасы, температуралы, электрлі және магнитті жолдардың механикалық деформацияланатын жолдарының өзара байланыс эффектілерінің, денелердің геометриялық тұрғызылуының дамуы болып табылады.

Берілетін зерттеудің нәтижесінде бұралу, иілу процестерінің қарастырылуы, деформацияланатын қатты дененің механикасы, құрылыс механикасы, гидродинамика, геофизика ғылымдарының бөлімдерінде жақсы жетістіктерге алып келеді.

Жұмыстың ауқымдылығы - бұл серпімді дененің формасының өзгеруінің жаңа этаптарының теориялық зерттелуі, динамикалық деформацияланатын серпімді материалдардың жаңа моделін өңдеу, белгілі модельдер шегінде тегіс және кеңістік есебінің көптеген класын математикалық әдіспен зерттеу тиімділігі, серпімді параметрлердің әсеріне негізделген негізгі механикалық факторлардың теориялық талдауы болып табылады.

Берілген облыста теориялық және қолданбалы зерттеулердің санына қарамастан диссертациялық жұмыстың негізгі бөлімінде көрсетілген жалпы сипаттама бойынша көптеген есептердің шешілуін әлі де болса өңдеу қажет.

Зерттелетін жұмыстың теориялық және практикалық мәселелер жөніндегі пәлсапалық ойлар А. И. Бохонский, Л. АШмидт еңбектерінде тұңғыш сөз болса, С. Жүнісбеков еңбектерінен жалғасын тапты.

Зерттеудің мақсаты:

Сырық деформациясын математикалық әдістерді қолдып, ұтымды жолмен басқару есептерінің моделін құру.

Зерттеу нысаны:

Сырық деформациясын ұтымды басқару есептерін шешу.

Зерттеудің әдістері:

-математикалық амалдар негізінде шағын деформация кезінде және қоршаған орта есебіндегі жуықталған теңдеулерді пайдалану әдістері;

-кернеу және бастапқы жылжыту есебінсіз бекітілген немесе бос сырықтардың созылуы мен иілуі есебімен көлденең және бойламалы нақты теңдеулерді қолдану әдістері;

- Maple жүйесінде математикалық графикаларды модельдеу әдістері.

Зерттеудің ғылыми жаңалығы және теориялық мәні:

-қолданбалы есептер және механикадағы деформацияланатын қатты дене зерттелуінің даму заңдылығы анықталды;

-серпінді және бекітілген - серпімді динамикасының негізгі есептері түрлендірілді;

-құрылыс конструкцияларындағы қолданылатын материалдардың, серпімді қасиеттері анықталды.

Зерттеудің практикалық маңыздылығы:

құрылыс конструкцияларындағы деформацияланатын орта есебін шешудің әдіс-тәсілдері белгіленді;

- құрылыс конструкцияларындағы деформацияланатын орта есебінің тәжірибелік мүмкіндіктері табылды.

Кіріспе бөлімінде зерттеудің көкейкестілігі, зерттеу мақсаты, зерттеу әдістері, зерттеудің ғылыми жаңалығы, жарық көрген мақалалар сипатталып көрсетіледі.

Қорытындыда зерттеудің негізгі нәтижелері талданып тұжырымдалады және оларды пайдалануға байланысты ғылыми-әдістемелік ұсыныстар беріледі, мәселенің болашақта зерттелетін бағыттары көрсетіледі.

1. Сырықтардың деформациялануын ұтымды басқару есептеріндегі Лагранж көбецткіші және Ритц әдісі

В. Ритц әдiстерiн және Ж. Лагранж көбейткiштерін қолданып тұрақты және айнымалы қима сырықтарының серпiмдi деформациялануының үздiксiз басқарулары сыртқы жүктеменiң жағдайының сырықтар бойлай қозғалатын ақырын өзгерiсiнде табылған. Сапаның деформация белгiсiнiң шартты экстремумына есеп Лагранж есебінде көбейткiштердi қолданып теңдiктер түрiндегi шектеулер береді.

1. 1 Лагранж көпмүшеліктер әдісі . X= R n жиынында анықталған екі рет дифференциаланатын f ( x ) функциясының шартты экстремумда жалпы есебінің қойылуы (оптималдық және сапа критерийлерін ескере отырып) келесідей.

ϕ i ( xi , . . . , xn ) = 0, ( i =1, . . . , m ) қосымша шарттарын қанағаттандыратын f ( x , . . . , x ) функциясының экстремумын табу керек, мұндағы φ i- нақты сандар және m<n , және Лагранж функциясының қолданылуындағы L = f + ∑ λ i ϕ i , мұндағы λ i , . . . , λ m - еркін нақты сандар. Локальды экстремумның x* нүктесі келесідей қажетті шарттардан алынады:

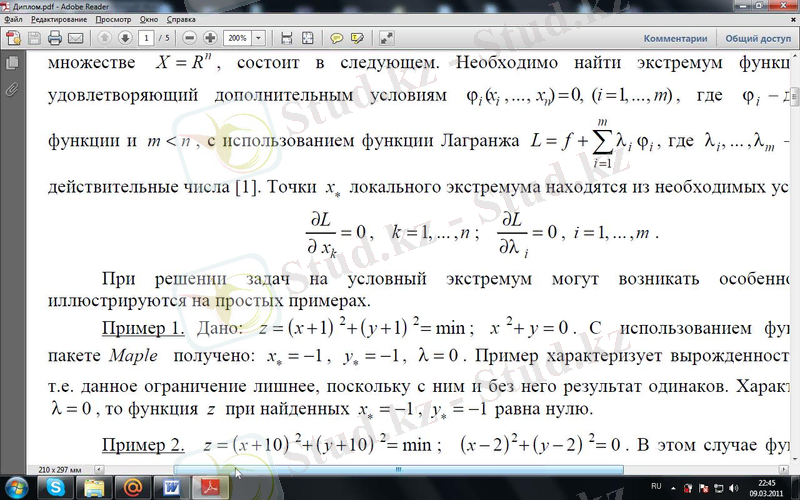
(1. 1. 1)

Шартты экстремум есептерін өте қарапайым мысалдардармен көрсетуге болады.

Мысал 1. Берiлген: 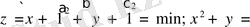Fsolve функцияны қолданып Maple пакетінде келесіні аламыз: 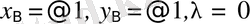Мысал шектеудiң артықтығын көрсетіп тұр, себебі шектеу бар болған жағдайда да, жоқ болса да нәтиже бірдей. Егер λ=0 болса онда z функциясы табылған 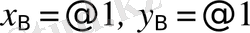мәндері бойынша нөлге тең.

Мысал 2. 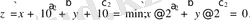Бұл жағдайда fsolve функциясы белгі мен шектеудің сәйкес келмейтіндігінен шешімді таппайды, яғни тапсырма дұрыс қойылмаған.

Лагранж көпмүшелігі егер айнымалы бөліктерін шектеулерден үздіксіз анықтау мүмкін емес болған жағдайда немесе әртүрлі аналитикалық түрлендіру жүктемелерімен қиындатылған жағдайда өте қолайлы әдіс.

1. 2 Ритцтың әдiсi. (Вальтер Ритц (1878-1909 ) - немiс физигi және математик) . Әдiс [2 ] бөлгiш банах кеңiстiгiнде функционалдың минимумының толық iздестiруге негiзделген, мысалы, толық нормаланған Rn кеңістігінде Эвклидті нормасы бар, бұл тәжірибе үшін қолайлы және сәйкес функцияны сәтті таңдаған жағдайда, бізге белгілі шешімнің дәрежесі полином дәрежесімен сәйкес келген жағдайда, В. Ритц әдісімен де дәл нәтиже алуға болады.

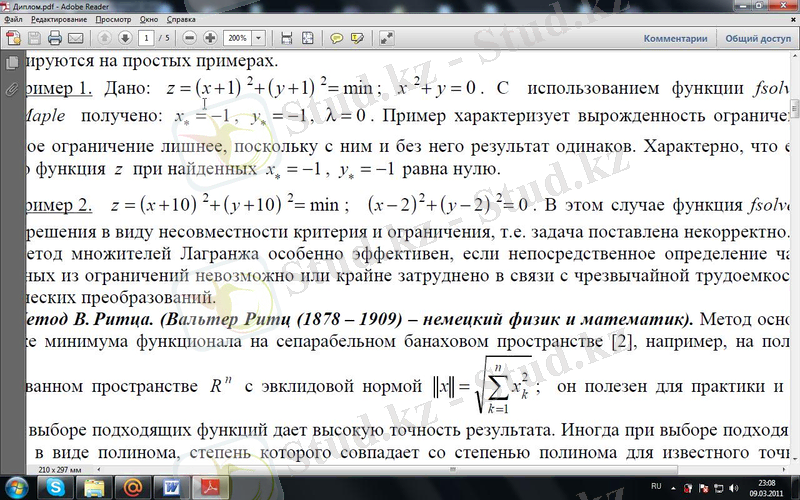Жеткілікті тәжірибелік әдістің дәлдігін екі тіректен ортаға қарай бағытталған күштің әсерінен арқалықтың майысуын көрсететін оте қарапайым мысалмен көрсетсек болады.

Толық энергияя функционалы келесідей болады:

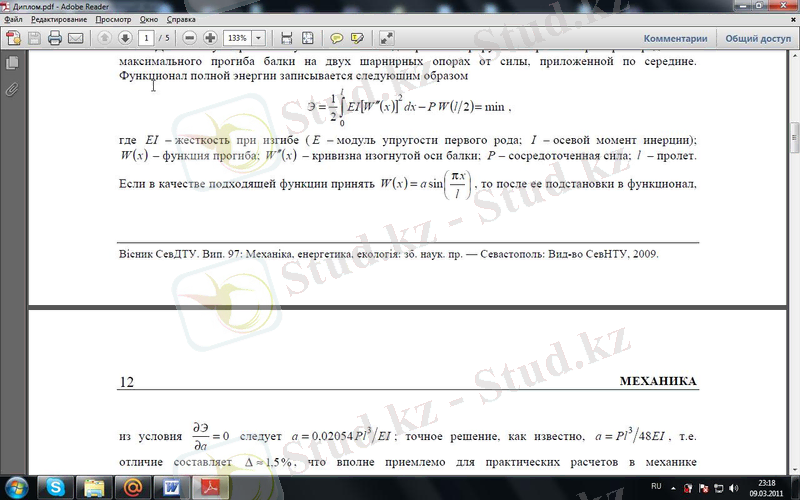
(1. 1. 2)

Мұнда EI- майысу кезіндегі қаттылық, ( E- бірінші дәрежелі тығыздық модулі, I- инерцияның өстік моменті) W(x) - қисаю функциясы, W´´(x) - арқалықтың майысқан өсінің қисығы, P- орнықтырылған күш, l- аралық.

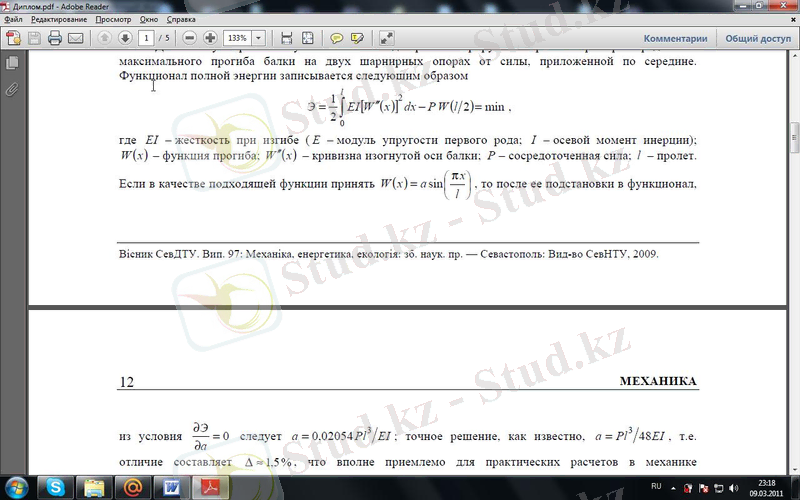
Егер сәйкес келетін функция ретінде алсақ, онда оны функционалға қойғаннан соң 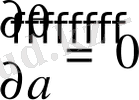шартынан болады; ал дәл шешімі, бізге белгілі а=Pl/48El, яғни қатынас Δ=1, 5%, бұл механикадағы қатты дененің деформациясы үшін толықтай қабылдалады.

1. 3 Деформациялануды ұтымды басқару есебінiң қойылуы .

Қатты заттар деформациялануын ұтымды басқару есептерi қатты емес бөлшектердi кең сыныптың автоматты токарлық өңдеуде, [3-5] ғарыш кеңiстiгiнде түпкi қаттылықтың манипуляторларының қолдарының қолдануында, тарқату және iрi қатты емес конструкциялардың құрастыру жағдайында көкейкестi мәселе болып отыр. Басқарылатын деформациялану есебінiң қойылуы сыртқы жүктеменiң мимырттауында келесi түрде берілмек. Деформацияланатын қатты дененің механикалық әдiстерi (Мысалы, сырық үшін - [3 ] бастапқы параметрлердiң әдiсiмен ) шиеленiстi-деформациялық күй суреттеледi - (берілген баяу қозғалатын жүктемені және анықталуы керек орнықтырылған басқару әрекеттері-күш пен моментті есепке ала отырып) . Деформациялық сапа белгісі берілген (ұтымдылықтың белгiсi) және шектеулер (теңдiктердiң түрiнде) шиеленiстi- деформациялық күйге. Табу керек: шектеулердi есепке ала отырып деформация белгiсiнiң минимумын қамтамасыз ететiн басқаруларды.

Зерттеулердiң мақсаты Ритц әдiстерi мен Лагранж көбейткiштерінің бiр уақыттағы қолданылу тиiмдiлiгiнiң бағасы және сырықтардың үздiксiз серпiмдi деформациялануын ұтымды басқарудың жаңа есептерiнiң шешiмiнде болып табылады. Бұл әдiстердiң қолданылуы мысалдарда келтiредi.

1. 4 Деформацияның потенциялдық энергиясы.

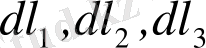
Дененің қарапайым бөлігіндегі потенциалдық

энергияны анықтау үшін оның бойынан

қырлары 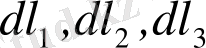, беттері басты

ауданшалармен сәйкес келетін қарапайым

параллипипедті бөліп аламыз.

Параллипипедтің әрбір бетінде, оған

перпендикуляр бағытта кернеу мен ауданының

көбейтіндісіне тең күш әсер етеді. (6. 3-сурет) .

6. 3-сурет

Энергияның сақталу заңы бойынша, деформацияның потенциялдық энергиясы параллипипедтің беттеріндегі сыртқы күштердің жұмысына тең. Сыртқы күштердің әсерінен паралипипедтің қырлары келесі шамаларға ұзарады.

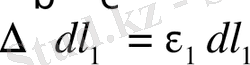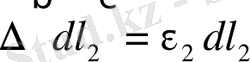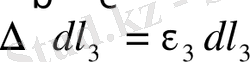; ; . (1. 4. 3)

Сондықтан потенциялдық энергияға тең сыртқы күштердің жұмысы

(1. 4. 4)

Мұндағы әрбір қосылғыш 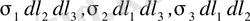статикалық түрде әсер етуші күштердің өз бағытындағы сәйкес 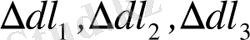орын ауыстыру аралығындағы жұмысы. Соңғы өрнектегі ұзару шамаларының орындарына өздерінің мәндерін қойсақ

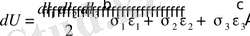
(1. 4. 5)

dU-ды алғашқы көлемге бөлсек, бірлік көлемге сәйкес потенциалдық энергия немесе толық меншікті потенциалдық энергия анықталады.

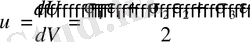(1. 4. 6)

Гуктың жалпылама заңынан

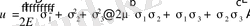(1. 4. 7)

Оның өлшем бірлігі кНм/ 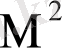(кН/ 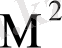) т. с. с.

Сыртқы күштердің әсерінен қарапайым параллипипедтің шамасы келесі шамаға өзгереді.

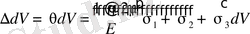(1. 4. 8)

Параллилопипедтің көлемі мен оның пішіні өзгереді, яғни оның қырлары әртүрлі шамаға ұзарады. Параллипипедтің барлық беттерінде бірдей 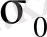кернеу әсерінен оның пішіні өзгермейді, ал көлемі (30. 3) формуласы арқылы анықталады, яғни

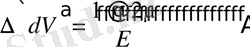(1. 4. 9)

Немесе

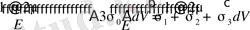(1. 4. 10)

Мұндағы

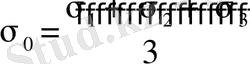(1. 4. 11)

Сонымен параллилопипедтің кернеулі күйін екіге жіктеуге болады. Олардың біріншісінде параллелопипедтің тек көлемі өзгереді, бұл күйдегі потенциалдық энергия көлемі өзгеретін потенциалдық энергия.

Екінші күйде параллипипедтің көлемі өзгермейді, тек оның пішіні өзгереді. Параллелопипедтің бойындағы жиналған потенциалдық энергия пішіні өзгеретін потенциалдық энергия.

Тек көлемді өзгертетін меншікті потенциалдық энергияны анықтау үшін (29. 3) өрнегіндегі 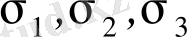кернеулерін 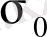кернеуімен алмастырады.

(7. 3, б-сурет)

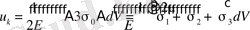(1. 4. 12)

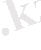
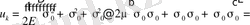
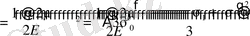
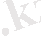(1. 4. 13)

Немесе

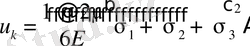
(1. 4. 14)

Тік кернеулердің қосындысы тұрақты болатындықтан

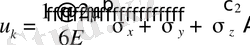(1. 4. 15)

Тік пішінді өзгеретін меншікті потенциалдық энергияны анықтау үшін (1. 4. 10) өрнегіндегі 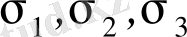кернеулерді 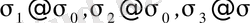кернеулерімен алмастырамыз.

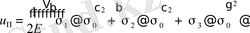
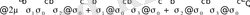. (1. 4. 16)

(29. 3) -ті ескере отырып, түрлендіруден соң

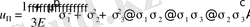(1. 4. 17)

Көлемді және пішінді өзгертетін меншікті потенциалдық энергиялардың қосындысы толық меншікті потенциалдық энергияға тең.

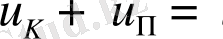
(1. 4. 18)

Меншікті потенциалдық энергия арқылы денедегі потенциалдық энергияны анықтауға болады.

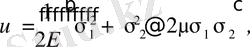
(1. 4. 19)

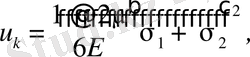
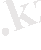(1. 4. 20)

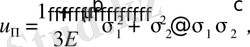(1. 4. 21)

Немесе басты кернеулерді (7. 3) өрнегімен алмастырсақ

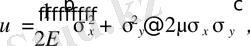
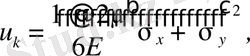(1. 4. 22)

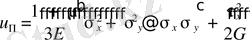
Мұндағы 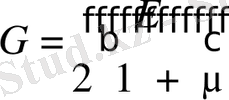−екінші ретті серпімділік модулі.

Жоғарыда барлық формула тек кернеулер пропорционалдық шектен аспаған жағдайда орындалады.

1. 5 Консолды сырықтың деформациялануын басқару.

Есеп 1. Консолды сырықтың схемасы 1-ші суретте көрсетiлген. W(a) 2=min (1) қамтамасыз ететін P және М басқарушы әсерлерін табу керек

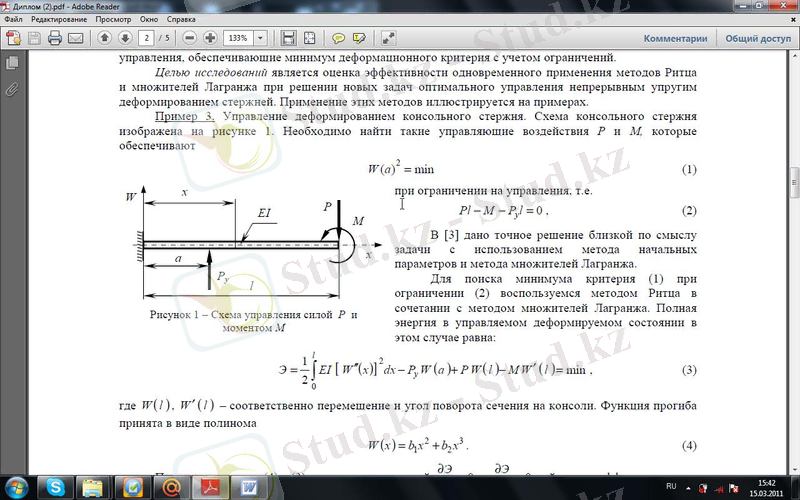Басқаруға шектеу қойғанда, яғни

(1. 5. 23)

[3] -те бастапқы параметрлер және

Лагранж әдістерін қолданып шығарған

мағынасы жағынан жақын есептің дәл

шешімі берілген.

(1) - ші теңдеудің минимумын іздеу

үшін

(2) - ші шектеу қойылған жағдайда

5. 1 сурет Лагранж көбейткішімен біріккен Ритц

әдісін қолданамыз.

Басқарылудағы деформация күйінде толық энергия бұл жағдайда мынадай болады:

- min (1. 5. 24)

Мұндағы W(l) , W´´(l) - сәйкесінше орын ауыстыру және консолмен қиылысу кезіндегі бұрылу бұрышы. Иiлiстiң функциясы полином түрінде қабылданған

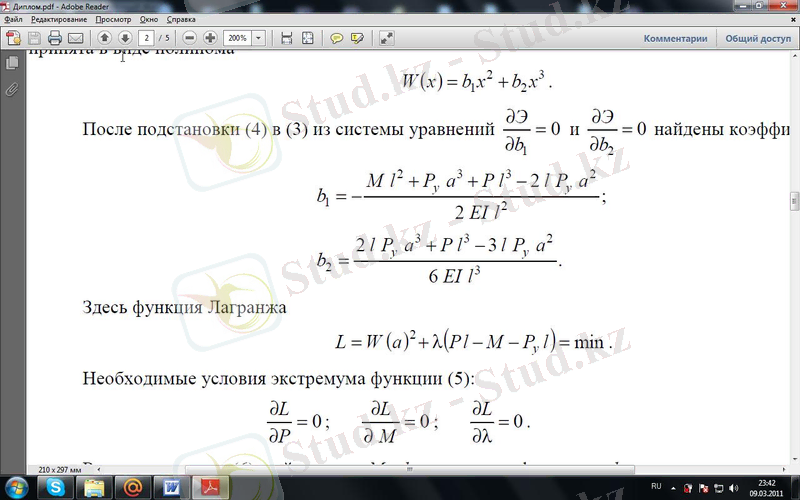
(1. 5. 25)

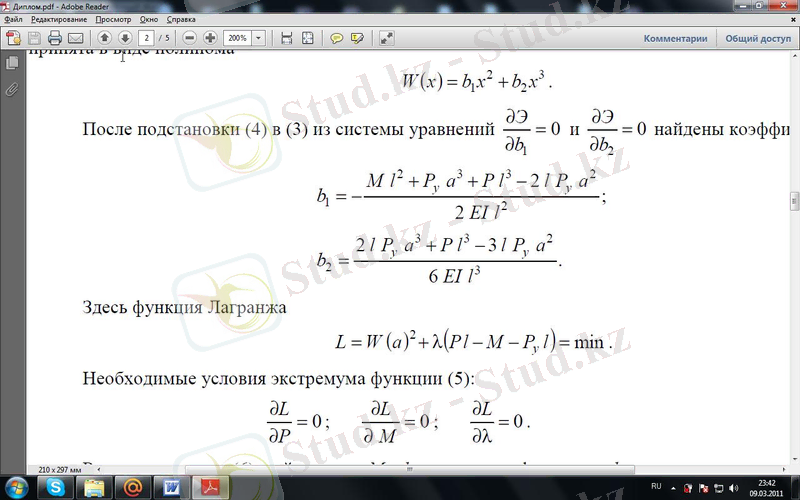
(4) ші теңдеуді (3) ке қойғаннан соң және теңдеулер жүйесінен келесідей коэффициенттер табылды:

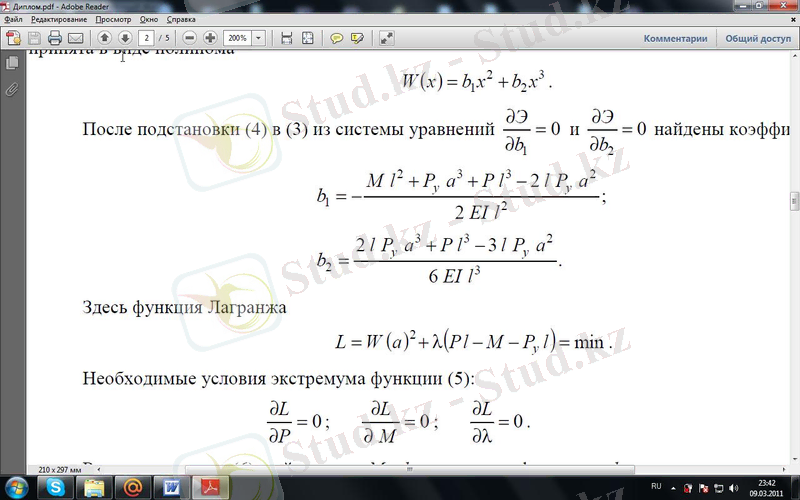
(1. 5. 26)

Мынау Лагранж функциясы:

−min 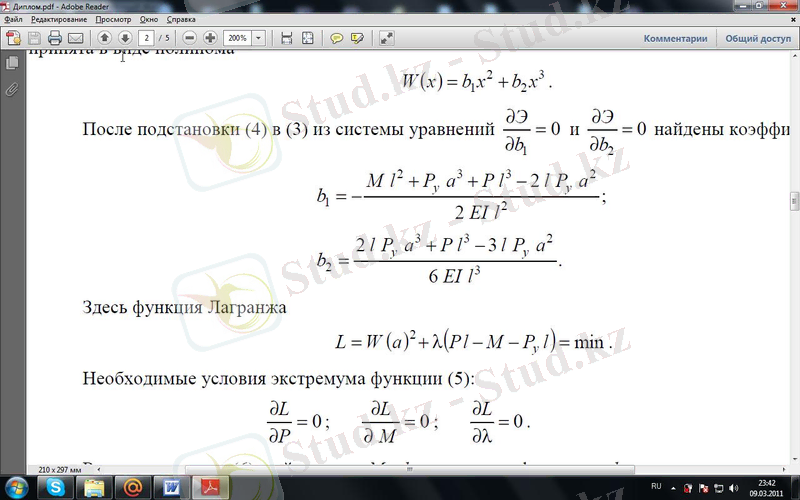(1. 5. 27)

(5) -ші функцияның экстремумы үшін қажетті шарттар:

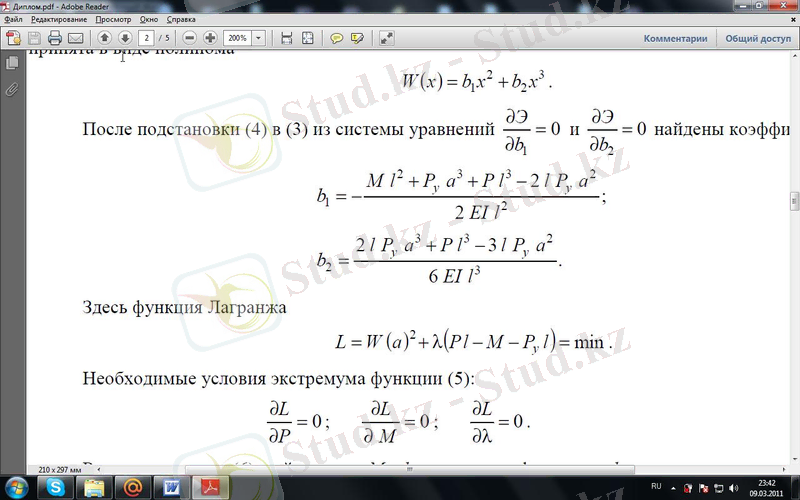
(1. 28)

(6) -шы жүйенің solve функциясының көмегімен Maple -да табылған шешімі:

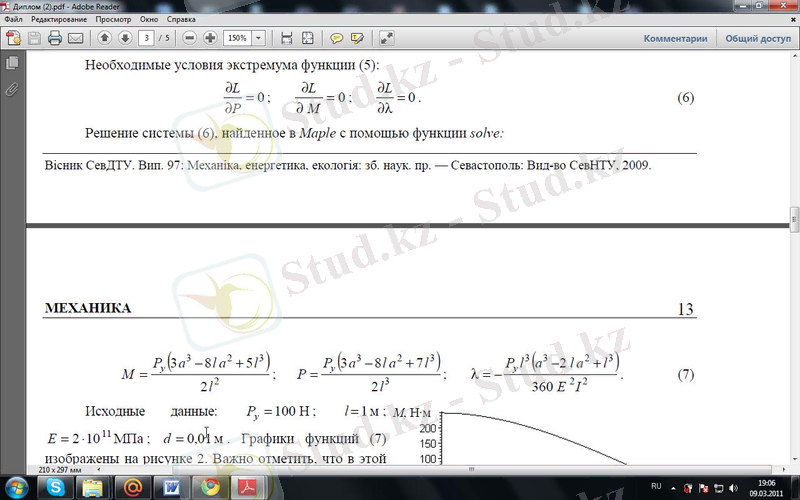
(1. 5. 30)

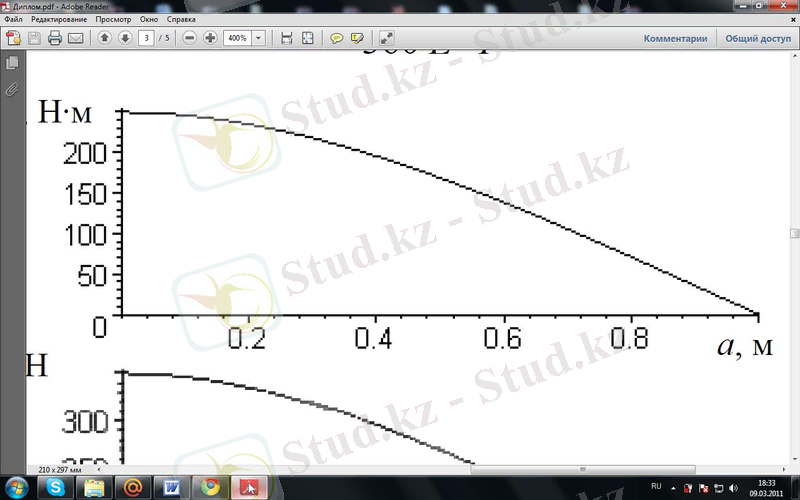
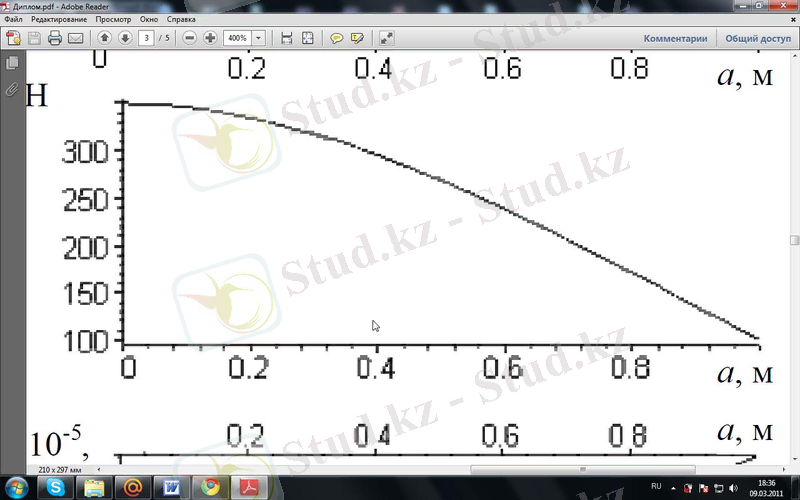
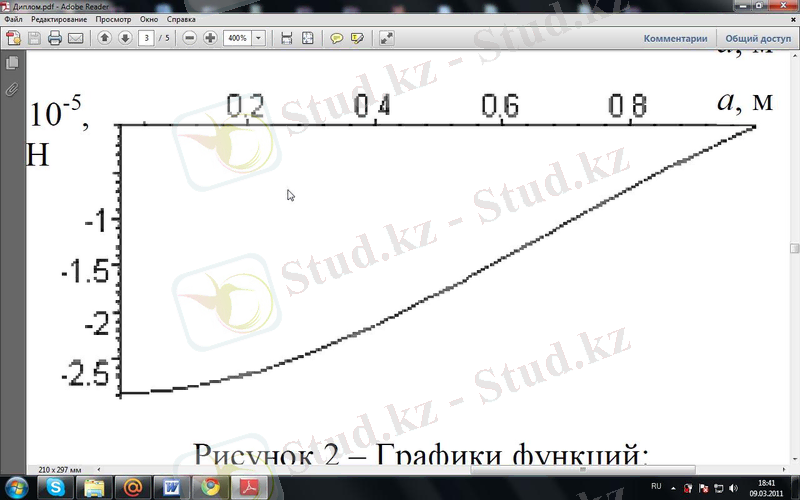
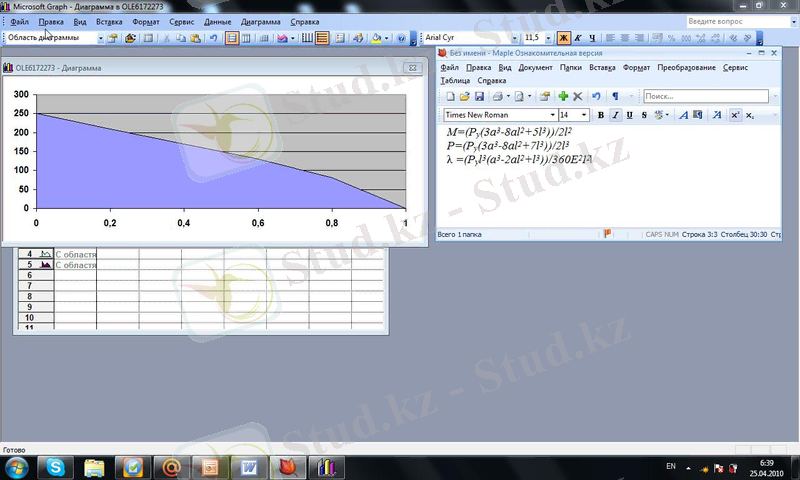
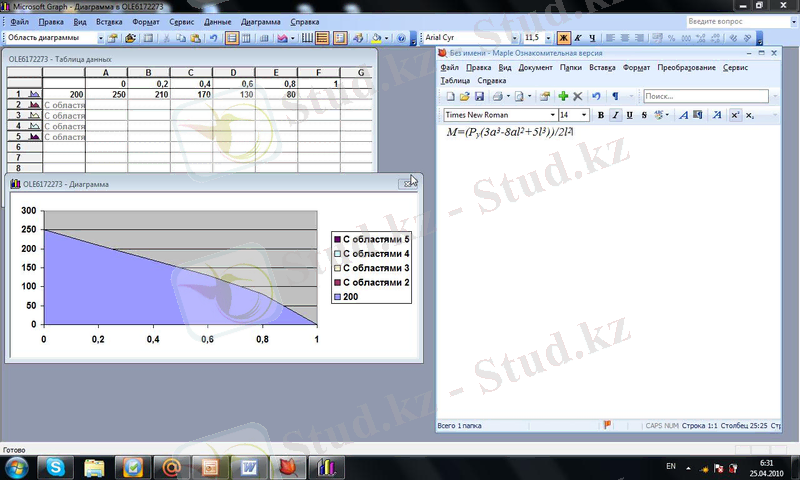
(7 ) функция графигінің бастапқы

деректерi 2- суретте көрсетiлген.

Бұл есепте шешiмдi алуға Лагранж-

дың әдiстiң қолдануынсыз қол

жеткізуге болатынын атап өту қажет.

Айнымалы қиманың сырығының

деформациялануын басқаруда Ритц

әдісінің орны ерекше, өйткенi өлденең

қиманың остік инерция моментi ұзына

бойына координатаның функциясы

болып табылады жәнекөп жағдайда

қисайған осьтің дифференциялдық

теңдеуін үздіксіз интегралдау

барысында, егер интеграл астындағы

функция алымы мен бөлiмі бар

бөлшек сан болса, интеграл есептеп

шығару қиынға соғады.

2. Материалдар кедергісінің негізгі болжамдары .

Құрылылым элементтерін беріктікке, қатаңдыққа, орнықтылыққа зерттегенде есептеуді жеңілдету үшін болжамдар қабылданады. Тәжірибе мен серпімділік теаориясының дәлірек есептеу негіздеріне сүценіп болжамдарды матеиалдар кедергісіне пайдалануға болатындығы дәлелденген. Негізгі болжамдарға тоқталсақ:

Құрылым материалы біртекті, толық, яғни оның қасиеттері пішіні мен өлшемдеріне тәуелсіз, барлық нүктелерінде бірдей. Осының негізінде дененің дискретті атомдық құрылысы ескерілмейді.
Құрылым материалы изотропты, яғни барлық бағытта оның қасиеттері бірдей.

Көптеген есептерді шығарғанда қолданылатын гипотеза, кейбір материалдар үшін шартты түрде қолданылады(мысалы ағаштың, талшық бойымен өсіне көлденең бағыттағы қасиеттері әртүрлі) . Әртүрлі бағыттағы қасиеттері әртүрлі, онда материалдар анизотропты материалдар деп аталады.