Телемеханикалық жүйелердегі кодтар

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 64 бет
Таңдаулыға:

КІРІСПЕ

Бұгінгі күні ақпарат алмасуды эффективті ұйымдастыру адамдардың нәтижелі қызметінің басты шартына айналды. Қоғамның нормальді функционалдауы үшін қажетті ақпарат көлемі өндірістік күштердің дамуының квадратына пропорционал өсуде. Ақпаратты түрлендірудің барлық сатыларында автоматтандыру әдістерін қолдану байланыс арнасының функционалдауының эффективтілігін жоғарлатады.

Ақпаратты жіберу дәлдігін жоғарлату мәселесі реалды байланыс арналары мен ақпаратты жіберу кезінде қойылатын талаптар арасындағы сәйкестіктің болмауымен байланысты. Байланыс желілерінде 10 ^-6 -10 ^-9 -нен кем емес дәлдікті қамтамасыз ету керек. Ал реалды байланыс арналарында қарапайым кодтарды пайдаланғанда дәлдік 10 ^-2 - 10 ^-5 -тен аспайды.

Бүгінгі таңда дәлдікті жоғарлатудың бір жолы ретінде бөгеуілдерден қорғалған (коррекциялаушы) кодтарды пайдалану жатыр.

Соңғы кездегі бөгеуілдерден қорғалған кодтар теориясы мен практикасының дамуының бойшаңдығы - алдымен, берілгендерді телеөңдеу құрылғыларын, есептеу жүйелері мен желілерін, аумақтық басқару жүйелерін, ғылыми зерттеуді автоматтандыру жүйелерін жасаумен байланысты. Аталған жүйелерде ақпаратты жіберу, өңдеу және сақтаудың шынайылығына қойылатын жоғары талаптар - қатені табу және түзету мүмкіндігін қамтамасыз ететін ақпаратты кодтау керектігін дәлелдеді.

Бұл тұрғыдан қарастырғанда Рид-Соломон кодтарының маңызы өте жоғары. Бұл аталмыш код өзінің бірқатар қасиеттеріне және техникалық жүзеге асырылуының қарапайымдылығына байланысты ақпаратты жіберудің дәлдігін талап ететін жүйелерде кең қолданыс тапты.

Бипломдық жобалау барысында Рид-Соломон кодының бес және алты разрядты алфавиттері құрылып, бес разрядты жағдай үшін кодтау және декодтау процедуралары мен техникалық жүзеге асырылулары қарастырылды. “Қолданбалы ақпараттар теориясы” пәнінің арналық кодтау бөлімінің электронды оқулығы жасалды.

Дипломдық жобалаудың түсініктеме жазбасы сегіз бөлімнен тұрады.

Бірінші бөлімде телемеханикалық жүйелердегі кодтар, олардың қасиеттері мен ерекшеліктері, кодтау теориясының негізгі анықтамалары мен түсініктері келтірілген.

Екінші бөлімде Рид-Соломон кодтарының құрылуы, кодтау және декодтау, қателерді табу және түзету процедуралары қарастырылған.

Рид-Соломон кодының кодері мен декодерінің функционалды сұлбалары, олардың System View бағдарламасында жүзеге асырылулары үшінші бөлімде келтірілген.

Жобаның төртінші бөлімінде бес разрядты Рид-Соломон кодының кодері мен декодерінің қағидалы сұлбалары құрылды.

Бесінші бөлімде дайындаудың технологиясы мен конструкциясы жасалған.

Алтыншы бөлімде “Қолданбалы ақпараттар теориясы” пәнінің арналық кодтау бөліміне арналған электронды оқулық құрылған.

Жетінші бөлім берілген электронды оқу құралын енгізудің экономикалық тиімділігінің есептелуі орындалған.

Сегізінші бөлім еңбек қорғау және тіршілікті қауіпсіздігін қамтамасыздандыру мәселелеріне арналған.

АНДАТПА

Берілген дипломдық жобада бөгеуілдерден қорғалған кодтар қатарына жататын Рид-Соломон кодтары қарастырылып, бес разрядты жағдай үшін кодтау, декодтау процедуралы толық қарастырылған. Кодер мен декордің функционалды және қағидалы сұлбалары құрылып, System View бағдарламасында олардың жүзеге асырылулары қарастырылған. “Қолданбалы ақпараттар теорисы” пәнінің арналық кодтау дөліміне арналған электронды оқулығы жасалды.

АННОТАЦИЯ

В данном дипломном проекте исследованы коды Рида-Соломона являющиеся помехоустойчевыми. Полностью рассмотрены процедуры созданя алфавита, кодирования и декодирования. Разработаны функциональные и принципиальные схемы кодера и декодера для пятиразрядного случая и рассмотрена их реализация при помощи программы System View. Создан электронный учебник раздела кональное кодирование дисциплины “Прикладная теория информаций”.

МАЗМҰНЫ

КІРІСПЕ

1 ТЕЛЕМЕХАНИКАЛЫҚ ЖҮЙЕЛЕРДЕГІ КОДТАР

1. 1 Бөгеуілден қорғалмаған кодтар

1. 2 Бөгеуілден қорғалған кодтар

1. 2. 1

2 РИД-СОЛОМОН КОДЫ КӨМЕГІМЕН АҚПАРАТТЫ ЖІБЕРУ ЖӘНЕ ЗЕРТТЕУ

2. 1 Рид-Соломон кодтары

2. 2 Кодерлеу

2. 3 Декодерлеу

2. 3. 1 Синдромды есептеу

2. 3. 2 Қатені табу

3 РИД-СОЛОМОН КОДЫНЫҢ ФУНКЦИОНАЛДЫ СҰЛБАСЫНЫҢ SUSTEM VIW БАҒДАРЛАМАСЫ КӨМЕГІМЕН ІСКЕ АСЫРЫЛУЫ

3. 1 Кодердің сұлбасы

3. 2 Декодердің сұлбасы

4 ҚАҒИДАЛЫ СҰЛБАЛАРДЫ ҚҰРУ

4. 1 Кодтау құрылғысының қағидалы сұлбасы

4. 2 Декодтау құрылғысының қағидалы сұлбасы

5 ДАЙЫНДАУДЫҢ ТЕХНОЛОГИСЫ МЕН КОНСТРУКЦИЯСЫ

6 БАҒДАРЛАМАЛЫҚ ҚАМТАМАСЫЗ ЕТІЛУІ

6. 1 HTML тілінің негіздері

6. 2 Пайдаланылған негізгі тегтер анализі

7 ЭКОНОМИКАЛЫҚ БӨЛІМ

8 ЕҢБЕК ҚОРҒАУ БӨЛІМІ

ҚОРТЫНДЫ

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1 ТЕЛЕМЕХАНИКАДА ҚОЛДАНЫЛАТЫН КОДТАР

Кодтау- белгілі бір ережеге сәйкес орындалатын, дискретті хабарды дискретті сигналға түрлендіру. Кері процесс- декодтау- бұл кодтау ережесін ескере отырып жүзеге асырылатын, дискретті канал шығысындағы сигнал бойынша дискретті хабарды қалпына келтіру процесі.

Код- дискретті хабарды білдіретін, шартты сигналдар жиындығы.

Арналық кодтар екі үлкен класқа бөлінеді. Олар бөгеуілден қорғалған кодтар және бөгеуілден қорғалмаған кодтар.

Бөгеуілден қорғалмаған кодтар

Кез-келген дискретті хабарға немесе хабар белгісіне қандай-да бір реттік нөмір беруге болады. Бұл кезде хабарды жіберу немесе сақтау - сандарды жіберу немесе сақтауға әкеледі. Сандарды қандай-да бір санау жүйесінде өрнектеуге болады. Осыған байланысты берілген санау жүйесіне негізделген код пайда болады. Ақпаратты жіберу жүйсінде қолдану, сақтау және түрлендіру тұрғысынан санау жүйесі мен олардың негізінде құрылған кодтарды салыстырамыз.

Қазіргі уақытта санау жүйесін құрастыруда көбіне танылып отырған - позициялық принцип. Әрбір символдың (санның) мәні оның орнынан, санды өрнектейтін символдар қатарындағы позициясынан, тәуелді. Әр бір келесі разрядтың бірлігі алдыңғы разрядтың бірлігінен m рет үлкен, мұндағы m - санау жүйесінің негізі. Жалпы санын разрядтар бойынша қосу арқылы аламыз:

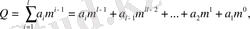
мұндағы i- берілген санның разрядының номері; l- разрядтар саны ; 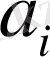- 0-ден m-1 -ге дейін өзгеретін, кез-келген бүтінсанды мәнге ие болатын көбейткіштер.

Санау жүйесінің негізі үлкен болған сайын, берілген санды өрнектеу үшін разрядтар саны азырақ болады, сондықтан оны жіберу үшін аз уақыт керек.

Бірақ, негізінің өсуіне байланысты байланыс желісіне және түрлі символдарға сәйкес келетін элементарлы сигналдарды тану мен жасау аппаратурасына қойылатын талаптар айтарлықтай өседі. Есептеу құрылғыларының логикалық элементтерінің, бұл жағдайда, орнықтылық күйлері көбірек болуы керек.

Бұл барлық жағдайларды ескере отырып, кез-келген санды сипаттау үшін әр түрлі символдардың саны мен l разрядтар саны арасындағы қатынастың минималды болуын қамтамасыз ететін жүйелерді таңдаған жөн.

Барлық жүйелерді оларға сәйкес сәйкес логикалық элементтердің физикалық іске асу тұрғысынан, сондай-ақ, арифметикалық және логикалық әрекеттері орындалуының қарапайымдылық тұрғысынан салыстыра келе - екілік жүйеге ерекше мән береміз. Шынында да, бұл жүйеге сәйкес келетін логикалық элементтердің екі орнықтылық күйі болуы керек. Бұл жағдайда сигналдарды ажырату мәселесі - сигналдарды көру (импульс бар ма, жоқ па) мәселесіне айналады, бұл жеңілірек.

Арифметикалық және логикалық әрекеттер де екілік жүйеде қарапайымырақ жүзеге асады.

Қосу, алу және көбейту кестелеріне төрт теңдік қана кіреді:

Қосу Алу Көбейту

ережелері ережелері ережелері

0+0=0 0-0=0 0⋅0=0

0+1=1 1-0=1 0⋅1=0

1+0=1 1-1=0 1⋅0=0

1+1=10 10-1=1 1⋅1=1

Кодтау және декодтау кезіндегі кең таралған тәсіл - модуль бойынша қосу. Екілік жүйеде бұл амал да ең қарапайым және мына теңдіктермен орындалады:

0⊕0=0 1⊕1=0

0⊕1=1 1⊕0=1

Екілік санау жүйесінен үйреншікті ондық жүйеге ауыстыру қиын емес. Қайта есептеу үлкен разрядтан басталады. Егер келесі разрядта 0 тұрса, онда алдыңғы разряд саны екі есе көбейеді. Ал егер келесі разрядта бір болса, онда алдыңғы разряд екі есеге көбейгеннен кейін нәтиже 1-ге көбейеді.

Сонымен, логикалық және арифметикалық операцияларды жүзеге асыру мен сақтау үшін ең тиімді екілік код. Бірақ ол ақпаратты енгізіп шығару кезінде қолайсыз. Сонымен қатар, мұндай сандарды қағазда жазу көп орын алады. Сондықтан екілік жүйеден басқа бір жағынан ондық және екілік жүйелерге оңай келтірілетін, екінші жағынан жазу кезінде ықшам болатын, жүйелер қолданыс тапты. Мұндай жүйелерге сегіздік, он алтылық және екілік - ондық жүйелер жатады.

Сегіздік жүйеде барлық мүмкін болатын сандарды жазу үшін 0-ден 7-ге дейінгі сегіз сан пайдаланылады.

Сегіздік жүйеде сандарды жазу қысқарақ болатындықтан, ол бағдарламалау кезінде қосалқы жүйе ретінде пайдаланылады.

Екілік және ондық жүйелердің артықшылықтарын бірге пайдалану үшін екілік - ондық кодтарды пайдаланады. Мұндай кодта ондық сандарды төртразрядты екілік сандар түрінде жазады. Төрт разряд көмегімен 16 әртүрлі комбинацияларды құрамыз. Олардың кез-келген оны екілік - ондық кодты құра алады. Ең тиімді болып 8-4-2-1 коды табылады. Бұл код өлшенген кодтар қатарына жатады. Код атауындағы сандар сәйкес екілік разрядтардағы бірлер салмағын көрсетеді. Әдетте, екілік - ондық код есептеу машинасына ондық түрде берілген сандарды енгізу кезінде пайдаланылады.

Бөгеуілден қорғалмаған кодтардың басты ерекшелігі - бір-бірінен бір разрядта ғана айырмашылығы бар комбинациялардың болуы, яғни d=1. Бұған да мысал ретінде екілік кодты алуға болады:

00 - (1) ;

01 - (2) ;

10 - (3) ;

11 - (4) .

Көрініп отырғандай, бұл жағдайда код аралығы бірге тең, себебі “00” “01”-ден бір позицияға өзгеше болып тұр. Байланыс арқылы біз “1” жіберуіміз қажет деп қарастырайық, яғни байланыс арнасына “00” сигналы келіп түседі, егер кіші разрядтағы байланыста бөгеу болатын болса, онда қабылдағыштың соңында “01” сигналы қабылданады, ол екіге сәйкес келеді.

Сондықтан, кодтың бұрмалануы - ақпараттың бұрмалануына әкеліп соғады, яғни ақпараттың дұрыс қабылданбауына бір ғана қате жеткілікті.

Екілік код ақпаратты тасымалдаушылардың кең тараған түрі болып табылады.

Мысалы, төртразрядты екілік код:

- (0) ;

0001 - (1) ;

0010 - (2) ;

0011 - (3) ;

0100 - (4) ;

0101 - (5) ;

0110 - (6) ;

0111 - (7) ;

1000 - (8) ;

1001 - (9) ;

1010 - (10) ;

1011 - (11) ;

1100 - (12) ;

1101 - (13) ;

1110 - (14) ;

- (15) .

Көрініп тұрғандай, екі код немесе код сөздерінің аралығы бірге тең, яғни d=1. Осыдан, бөгеуілге тұра алмайтын екілік кодтарды телемеханикалық ақпараттарды байланыс арнасы арқылы жіберу мүмкін емес.

Санау жүйелерінен ажырайтын кодтардың ішінде бір саннан екінші санға өткен кезде тек бір разрядта өзгеріс болатын кодтар үлкен практикалық мәнге ие. Мұндай кодтардың ішінде ең кең қолданыс тапқан код Грей коды. Оны әдетте, циклдік немесе рефлексті - екілік деп атайды. Грей кодын аналогты - цифрлі түрлендіру техникасында пайдаланады.

Кәдімгі екілік код Грей кодына бастапқы комбинацияны разряд оңға ығыстырылған дәл сондай комбинациямен модуль екі бойынша қосу арқылы түрлендіріледі. Кері түрлендіру кіші разрядтан басталып Грей кодындағы цифрлар санын қосу жолымен жүзеге асырылады. Егер модуль екі бойынша қосу нәтижесінде қосынды жұп болса, 0 жазылады, тақ болса, 1 жазылады.

Тікелей Грей кодынан ондық санға түрлендіру қиындықтар тудыратындығына байланысты, алдымен Грей кодынан екілікке, содан кейін екілікті ондыққа түрлендіру жүргізіледі. Ондық эквивалентке түрлендіру қиындығы Грей кодының басты кемшіліге болып табылады.

Жоғарыда айтылған кемшіліктер бойынша телемеханикада бөгеілден қорғалған кодтар қолданылмайды. Бұрмаланбаған кодтар кәдімгі кодтар деп аталады. Бұл кодтарға екілік код, бірлік - ондық код, екілік - ондық код, санды импульсті код, Морзе коды, Бодо коды, халықаралық телеграфтық код кіреді.

Кейбір негізгі бөгеілдерден қорғалмаған кодтарға тоқталып кетеміз.

Екілік - ондық кодта ондық санның әрбір разряды сәйкес бірлер саны түрінде жазылады. Разрядтар интерволдармен бөлінеді. Бұл код тіртекті емес. Оны сәйкес разрядтардың соңына нөлдерді жазу арқылы біртектіге түрлендіруге болады.

Санды - импульсті кодты кейде бірлік код деп те атайды. Кодты комбинациялар саны бір - бірінен берлер санымен ерекшеленеді. Мұнда

N=n

Морзе коды, кодты комбинациялар бір-бірінен ұзақтықтарымен ерекшеленетін, біртекті емес кодтар қатарына жатады. Мұнда сигналдар нүкте және тире түрінеде жіберіледі. Нүкте - бірмен жазылып, бір импульспен жіберіледі, ал тире - үш импульспен (араларында интервалсыз) жіберіледі. Нүкте мен тире арасындағы интервал нөлді береді.

Бөгеуілден қорғалған кодтар

Бөгеуілдерден қорғалған деп байланыс арналары арқылы жіберу кезінде пайда болатын қателерді тауып түзетуге мүмкіндік беретін кодтарды атайды.

Бөгеілдерден қорғалған кодтар теориясы Шенонның теориясына негізделеді:

1. Арнаның өткізу қабілетінен төмен хабар көзінің кез-келген өнімділігі үшін, барлық түзілген ақпаратты қатенің пайда болу ықтималдығы өте аз болатын, кодтау әдісі бар болады.

2. Хабар көзі өнімділігі арнаның өткізу қабілетінен жоғары болған кезде ақпаратты қатенің пайда болу ықтималдығы өте аз болатындай жіберуге мүмкіндік беретін кодтау бар болады.

Теорема ақпаратты дәл беру кезіндегі жүйенің мүмкін болатын эффективтілігінің теориялық шегін орнатады. Сонымен қатар, бөгеуіл бар кезіндегі арна арқылы ақпаратты жіберу кезінде қатенің пайда болуының өте аз ықтималдылығын қамтамасыз ету тек шексіз көп артықтылықты енгізу арқылы жүзеге асады деген тұжырымды жоққа шығарды. Теорема бойынша арнадағы бөгеуілдер ақпаратты жіберу дәлдігіне шектеулер орнатпайды. Шектеулер тек ақпаратты жіберу жылдамдығына әсер етеді.

Теорема көрсетілген идеалды жіберуді қамтамасыз ететін кодтарды құру жолдары туралы сұрақтарға жауап беру тұрғысынан конструктивті емес. Арнаның өткізу қасиетіне дейінгі ақпаратты жіберудің кез-келген шекті жылдамдығы үшін қате пайда болуының өте төмен ықтималдығы кодталатын символдар тізбегін шексіз ұзарту арқылы қамтамасыз етілетіндігін, атап кеткен жөн. Осылайша, бөгеуіл бар кездері қатесіз жіберу тек теория тұрғысынан мүмкін болады.

Ақпаратты қатенің пайда болуының өте аз ықтималдығы мен жоғары эффективтілікпен жіберу тек өте ұзын символды тізбектерді кодтау кезінде мүмкін болады. Практикада эффективтілік пен дәлдік дәрежесі келесі екі фактормен шектеледі: кодтау мен декодтау құралғыларының құны, өлшемі және жіберілетін хабардың кідіріс уақыты.

Бөгеуілден қарғалған кодтау, қабылданған символдар тізбегіне сәйкес келтін сигнал оған арнада болатын бөгеілдердің әсерінен кейін, басқа мүмкін болатын символды тізбектерге емес жіберілген символдар тізбегіне жақынырақ болатындай, жүзеге асырылуы керек. (Жақындық дәрежесі тізбектердегі әр түрлі разрядтар санымен анықталады. )

Бұл кодтау кезінде жіберілетін символдар тізбегін қосымша шарттарды қанағаттандыратындай етіп таңдауға мүмкіндік беретін артықтылықты енгізу арқылы жүзеге асырылады. Қосымша шарттар, қабылдаған жақта, қатені табуға және түзетуге мүмкіндік береді.

Мұндай қасиеттерге ие кодтарды бөгеуілден қорғалған деп атайды. Олар қателерді түзету үшін (коррекциялаушы кодтар) және табу үшін пайдаланылады.

1. 2. 1 Бөгеуілдерден қорғалған кодтар түрлері

Бүгінгі күні бар барлық бөгеуілден қорғалған кодтардағы мұндай шарттар олардың алгебралық құрылымына байланысты. Осыған байланысты оларды алгебралық кодтар деп атайды.

Алгебралық кодтарды екі үлкен класқа бөлуге болады: блокты және үздіксіз.

Блокты кодтар жағдайында кодтау процедурасы хабардың әр әріпіне (немесе бұл әріпке сәйкес келтін k символды тізбегін) n символды блокты сәйкестендіру арқылы жүзеге асырылады. Түрлендіру операцияларына тек көрсетілген k символдары қатысады және шығыстағы тізбек жіберілетін хабардағы басқа символдарға байланыссыз болады.

Егер n хабардың барлық әріптері үшін тұрақты болып қалатын болса, онда блокты код біртекті деп аталады.

Блокты кодтар бөлінетін және бөлінбейтін болып бөлінеді. Бөлінетін кодтармен кодтау кезінде шығыс тізбектер рольдері айқын бөлінетін символдардан тұрады. Олар арна кодері кірісіне кіретін символдармен сәйкес келетін ақпараттық символдар мен арна кодерімен бастапқы комбинацияға енгізілетін, артықтық (бақылау) символдары.

Бөлінбейтін кодтармен кодтау кезінде шығыстық тізбек символдарын ақпараттық және бақылау символдарына бөлу мүмкін емес.

Үздіксіз деп кодталатын ақпараттық символдарына бақылау символдарын енгізу, оларды тәуелсіз блоктарға бөлмей, үздіксіз түрде жүргізіледі. Үздіксіз кодтар, сонымен қатар, бөлінетін және бөлінбейтін болуы мүмкін.

Техникалық жүзеге асырылу тұрғысынан, бұл кластың ең қарапайым түрі орамдалатын кодтар болып табылады.

Кодтың қателерді тауып түзете алу қабілеті артықтық символдардың бар болуымен байланысты. Кодтау құрылғысының кірісіне k ақпарат символдарынан тұратын екілік символдар тізбегі келіп түседі. Шығыста оған n символдан тұратын тізбек сәйкес келеді, мұндағы n<k.

Жалпы барлығы 2 ^k түрлі және 2 ⁿ түрлі шығыс тізбектер бар бола алады. 2 ⁿ шығыс тізбектерінің тек 2 ^k тізбегі кіріс тізбектерге сәйкес келді. Оларды рұқсат етілген кодты комбинациялар деп атаймыз. Қалған мүмкін болатын 2 ⁿ - 2 ^k тізбектер пайдаланылмайды. Оларды рұқсат етілмеген деп атаймыз.

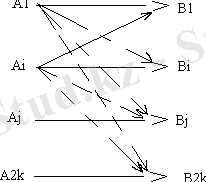
1. 1-Сурет - Арна арқылы хабарды жіберу жағдайлары

Жіберу кезінде ақпараттың бұрмалануы әсерінен кейбір символдар қате символдармен алмастырылады. Рұқсат етілген 2 ^k комбинациясының әр қайсысы бөгеуілдердің әсірінен кез-келген басқа комбинацияға айнала алатындығына байланысты 2 ⁿ ∙2 ^k мүмкін бұрмалану жағдайлары бар. Бұл санға кіретіні:

қатесіз жіберудің 2 ^k жағдайы;

табылмайтын қателерге сәйкес келетін басқа рұқсат етілген комбинацияларға өтудің 2 ^k (2 ^k -1) жағдайы;

анықтала алынатын рұқсат етілмеген комбинацияларға өтудің 2 ^k (2 ⁿ - 2 ^k ) жағдайы.

Яғни, жіберудің барлық мүмкін болатын жағдайларынан табылатын қате комбинациялардың саны келесідей:

2 ^k (2 ⁿ -2 ^k ) /(2 ^k ∙2 ⁿ ) =1-2 ^k /2 ⁿ .

Декодтаудың кез-келген әдісін рұқсат етілмеген комбинациялар жиынын, әрқайсысы бір рұқсат етілген комбинацияға сәйкес келтін, 2 ^k қиылыспайтын M _i ішжиындарға болу ретінде қарастыруға болады. M _i ішжиынына жататын рұқсат етілмеген комбинацияны алған кезде A _i рұқсат етілген комбинация жіберілді деген шешім қабылдайды. Қате егер қабылданған комбинация шын мәнісінде A _i -дан құралған жағдайда жөнделеді, яғни 2 ⁿ - 2 ^k жағдайда.

Жалпы рұқсат етілмеген комбинацияларға өтулер саны 2 ^k (2 ⁿ -2 ^k ) . Осылайша артықтық бар кезінде кез-келген код қателерді түзете алады.

Ішжиындарға бөлу әдісі берілген нақты код қандай қателерді анықтайтындығына байланысты болады.

Бүгінгі күнге дейін жасалынған кодтар өзара тәуелсіз қателерді және қателер бумаларын түзетуге арналған.

Өзара тәуелсіз қателер деп бұрмаланған символдардың кез-келген комбинациясының пайда болу ықтималдығы тек қана бұрмаланған символдар санына r және бір символдың бұрмалану ықтималдығына p байланысты болатын қателерді айтады.

Қате еселігі деп кодты комбинациядағы бұрмаланған символдар санын атайды.

Өзара тәуелсіз қателер кезінде n-разрядты кодты комбинацияның кез-келген r символының бұрмалану ықтималдығы

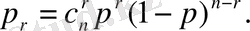
Егер р«1 екендігін ескерсек, онда бұл жағдайда ықтималдығы ең жоғары еселігі төмен қателер. Яғни, оларды бірінші кезекте тауып, түзету қажет.

Жоғарыда айтылғаннан, өзара тәуелсіз қателер кезінде, берілген комбинациядан символдардың ең кіші санымен өзгешеленетін кодқа өту ықтималдырақ екені көрініп тұр.

Кез-келген екі код комбинациясының өзгешелік дәрежесі - солардың арасындағы қашықтықпен немесе код аралығымен сипатталады. Ол комбинациялары бір-бірінен өзгешеленетін символдар санымен өрнектеледі және d арқылы белгіленеді.

Екілік кодтың екі комбинациясының арасындағы код аралығын алу үшін, бұл комбинацияларды модуль екі бойынша қосқандағы қосындының бірлер санын санау жеткілікті. Мысалға

1001101

⊕

1011011

000 d=7

Сонымен қатар, код аралығы кодтың қателерді түзету қасиетін анықтайды.

Барлық кодты комбинациялар d=1 кезінде рұқсат етілген болады. Мысалға, n=3 кезінде рұқсат етілген комбинациялар келесі жиынды құрайды: 000, 001, 010, 011, 100, 101, 110, 111.

Кез-келген бірлік қате берілген комбинацияны басқа рұқсат етілген комбинацияға түрлендіреді. Бұл артықтылық жоқ кезіндегі қателерді түзете алмайтын код жағдайы.

Егер d=2 болса, онда ешбір рұқсат етілген комбинация бірлік қате кезінде басқа рұқсат етілген комбинацияға өтпейді. Мысалға, n=3 үшін рұқсат етілген комбинациялардың ішжиыны олардағы бірлердің жұп болу принціпі бойынша құрыла алады:

000, 011, 101, 110

рұқсат етілген комбинациялар

001, 010, 100, 111

рұқсат етілмеген комбинациялар.

Код бірлік қателерді және тақ еселі қателерді (n=3 кезінде үштік) табады. Жалпы жағдайда r еселі қателерді табу керек кезде рұқсат етілген кодты комбинациялар арасындағы минималды аралық r-дан ең болмаса бірге көп болу керек, яғни

d _{т min} ≥r+1

Шынымен, бұл жағдайда еселігі r-дан аспайтын қате бір рұқсат етілген комбинацияны басқа рұқсат етілген комбинацияға түрлендіре алмайды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.