Ұлттық бірыңғай тестілеуге арналған стандартты емес 22 математикалық есеп және олардың толық шешімдері


Математикадан тест жинақтарындағы кейбір «стандартты емес» есептер
Жоспар
Кіріспе орнына . . . 1
Есеп шығару үлгілері . . . 2
Қолданылған әдебиеттер тізімі . . . 11
Кіріспе орнына
Елімізде жыл сайын жалпы орта мектепті бітіруші түлектер Ұлттық бірыңғай тестілеуде математика пәнінен де емтихан тапсыратыны баршаға аян. Талапкерлер үшін ҰБТ-да математикадан қиындықтар туғызатын есептер де кездесіп отыратындығы белгілі. Ол есептерді «қиын есептер», «күрделілігі жоғары есептер», «стандартты емес есептер» деп атайды. Бұл санаттағы есептерді шығару үшін қарапайым, стандартты есептерді шығара білу, формулаларды білу, қарапайым есептерді шешу жолдары мен айла-тәсілдерін білумен қатар, тереңірек математикалық білім мен жоғары деңгейдегі логикалық ойлау қабілеті талап етіледі. Жұмыста аталған тақырыпқа қатысты бірнеше есеп (дәлірек айтқанда, 22 есеп) толық шешу жолдарымен келтіріледі.
Есеп шығару үлгілері
1.
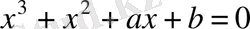 теңдеуінің бір түбірі
теңдеуінің бір түбірі
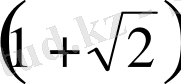 ,
,
 ,
,
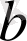 - бүтін сандар.
- бүтін сандар.
 мен
мен
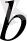 неге тең?
неге тең?
Шешуі.
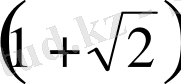 санын теңдеуге
санын теңдеуге
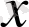 -тің орнына қоямыз. Қарапайым түрлендірулерден соң
-тің орнына қоямыз. Қарапайым түрлендірулерден соң
 теңдеуін аламыз.
теңдеуін аламыз.
 мен
мен
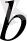 бүтін сандар болғандықтан,
бүтін сандар болғандықтан,
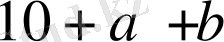 - рационал (бүтін) сан, ал
- рационал (бүтін) сан, ал
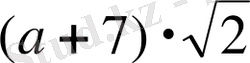 - иррационал сан. Рационал сан мен иррационал санның қосындысы нөлге тең бола алмайтындықтан,
- иррационал сан. Рационал сан мен иррационал санның қосындысы нөлге тең бола алмайтындықтан,
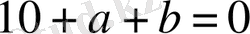 және
және
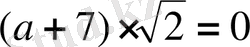 болуы керек. Сондықтан
болуы керек. Сондықтан
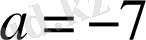 ,
,
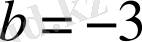 .
.
Жауабы.
 ,
,
 .
.
2.
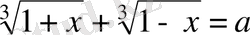 теңдеуін шешіңіз.
теңдеуін шешіңіз.
Шешуі. Теңдеудің екі жағын да кубтаймыз да, ортаңғы екі қосылғыштың ортақ көбейткіштерін жақша сыртына шығарамыз:
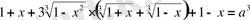 ,
,
 .
.
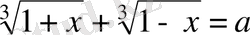 екенін ескерсек, соңғы теңдеу келесі түрге келеді:
екенін ескерсек, соңғы теңдеу келесі түрге келеді:
 .
.
Бұдан
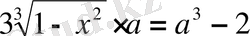 ,
,
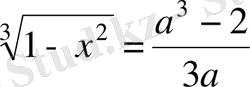 ,
,
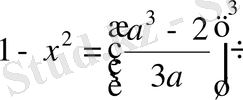 ,
,
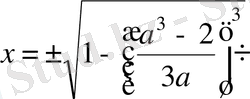 .
.
Жауабы.
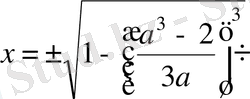 .
.
3
.
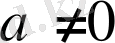 ,
,
 .
.
 теңдеулер жүйесін шешіңіз.
теңдеулер жүйесін шешіңіз.
Шешуі.
2-ші теңдеудің екі жағын да квадраттап, 1-ші теңдеуді оған мүшелеп бөлсек:
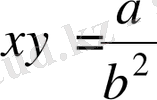 .
.
2-ші теңдеуден
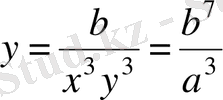 .
.
Сонда
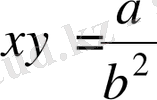

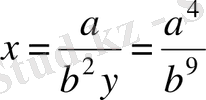 .
.
Жауабы.
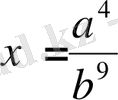 ,
,
 .
.
4.
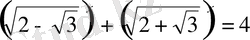 теңдеуін шешіңіз.
теңдеуін шешіңіз.
Шешуі.
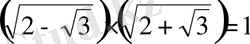 екенін байқаймыз. Бұдан
екенін байқаймыз. Бұдан
 . Сонда берілген теңдеу
. Сонда берілген теңдеу
 түріне келеді.
түріне келеді.
 алмастыруын енгізсек:
алмастыруын енгізсек:
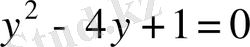 ;
;
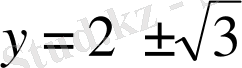 ,
,
 .
.
Жауабы.
 .
.
5. Сыныптағы оқушылардың әрқайсысы бірдей мөлшерде жинаған ақшалардың қосындысы 172 теңге 73 тиын болды. Сыныпта қанша оқушы болғаны?
А) 23. B) 21. C) 27. D) 24. E) 19.
Шешуі. 21, 27, 24 сандары 3-ке бөлінеді, ал 17273 (тиын) 3-ке бөлінбейді (оны тікелей тексеруге немесе 3-ке бөлінгіштік белгісін қолданып табуға болады), сондықтан 21, 27, 24 сандары есептің жауабы бола алмайды. Тікелей тексеру арқылы есептің жауабы 23 болатынын көреміз.
Жауабы. 23.
6.
 -ның қандай мәндерінде
-ның қандай мәндерінде
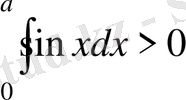 теңсіздігі орындалады?
теңсіздігі орындалады?
Шешуі.
 , яғни
, яғни
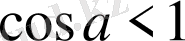 . Бұдан
. Бұдан
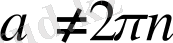 ,
,
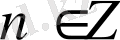 .
.
Жауабы.
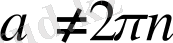 ,
,
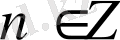 .
.
7.
 -ның қандай мәндерінде
-ның қандай мәндерінде
 функциясының кризистік нүктелері болмайтынын табыңыз.
функциясының кризистік нүктелері болмайтынын табыңыз.
Шешуі.
Берілген функцияның анықталу облысы:
 . Туындысын табамыз:
. Туындысын табамыз:
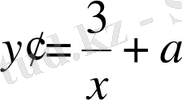 . Оны нольге теңестіреміз (кризистік нүкте болуының қажетті шарты) :
. Оны нольге теңестіреміз (кризистік нүкте болуының қажетті шарты) :
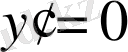 . Яғни
. Яғни
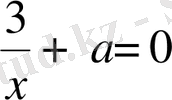 ,
,


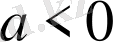 . Сонымен
. Сонымен
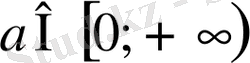 болғанда берілген функцияның кризистік нүктелері жоқ.
болғанда берілген функцияның кризистік нүктелері жоқ.
Жауабы.
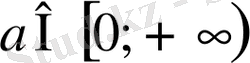 .
.
8.
Егер
 және
және
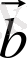 векторлары арасындағы бұрыш 30º, скаляр көбейтіндісі
векторлары арасындағы бұрыш 30º, скаляр көбейтіндісі
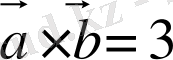 болса, онда осы векторлар арқылы салынған үшбұрыштың ауданын табыңыз.
болса, онда осы векторлар арқылы салынған үшбұрыштың ауданын табыңыз.
Шешуі. Скаляр көбейтіндінің анықтамасы бойынша
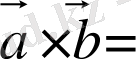
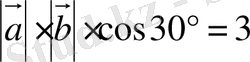

 .
.
Үшбұрыштың ауданының формуласы бойынша

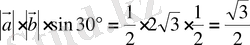 .
.
Жауабы.
 .
.
9.
Егер
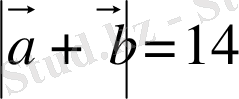 ,
,
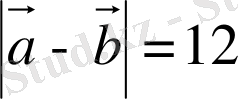 ,
,
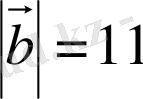 болса, онда
болса, онда
 табыңыз.
табыңыз.
Шешуі.
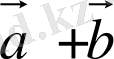 ,
,
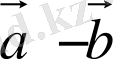 векторлары
векторлары
 және
және
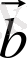 векторлары арқылы тұрғызылған параллелограмның диагональдары болады. Параллелограмның диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең:
векторлары арқылы тұрғызылған параллелограмның диагональдары болады. Параллелограмның диагональдарының квадраттарының қосындысы оның барлық қабырғаларының квадраттарының қосындысына тең:


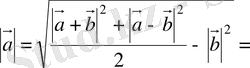
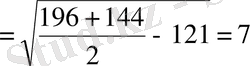 .
.
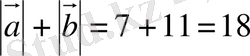 .
.
Жауабы. 18.
10.
Функцияның мәндерінің облысын табыңыз:
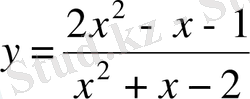 .
.
Шешуі.
Берілген функцияның анықталу облысы:
 ,
,
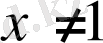 . Берілген функцияны түрлендірейік:
. Берілген функцияны түрлендірейік:
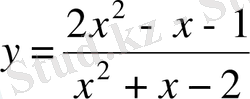

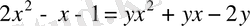


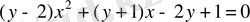 .
.
Дискриминанты
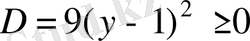 . Кез келген
. Кез келген
 үшін
үшін
 және келген
және келген
 үшін
үшін
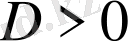 .
.
1)
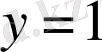


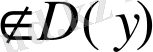 - анықталу облысы.
- анықталу облысы.
2)


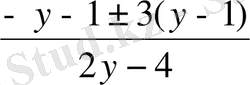
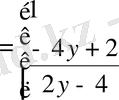
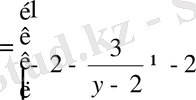 .
.
Жауабы.
 .
.
11.
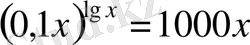 теңдеуінің түбірлерінің қосындысын жазыңыз.
теңдеуінің түбірлерінің қосындысын жазыңыз.
Шешуі.
Теңдеудің екі жағынан да ондық логарифм аламыз:
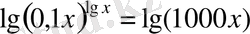 . Логарифмнің қасиеттерін ескерсек:
. Логарифмнің қасиеттерін ескерсек:
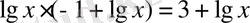 немесе
немесе
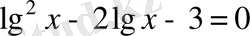 . Бұдан
. Бұдан
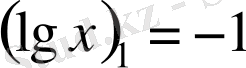 ,
,
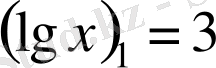 , яғни
, яғни
 ,
,
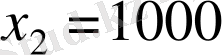 . Сонымен
. Сонымен
 .
.
Жауабы. 1000, 1
12.
Қосындыны есептеңіз:
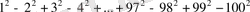 .
.
Шешуі. Қосылғыштарды тұрған ретімен қос-қостан топтап, азайту таңбасын жақшалардың алдына шығарып, екі санның квадраттарының айырмаларының формуласын қолданамыз:
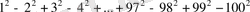


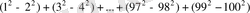


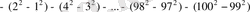


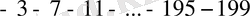 . Бұл бірінші мүшесі -3, айырмасы -4, соңғы мүшесі -199, мүшелерінің саны 50 болатын арифметикалық прогрессия, сондықтан
. Бұл бірінші мүшесі -3, айырмасы -4, соңғы мүшесі -199, мүшелерінің саны 50 болатын арифметикалық прогрессия, сондықтан
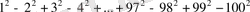



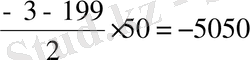 .
.
Жауабы.
 .
.
13.
Есептеңіз:
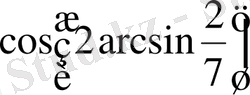 .
.
Шешуі.
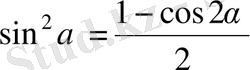 теңдігінен
теңдігінен
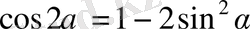 . Соңғы тең-дікті қолдансақ:
. Соңғы тең-дікті қолдансақ:


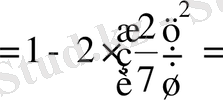
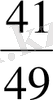 .
.
Жауабы.
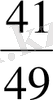 .
.
14 . Төмендегі сандардың ішінен ең үлкенін табыңыз:
А)
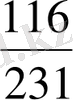 . В)
. В)
 . С)
. С)
 . D)
. D)
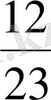 . E)
. E)
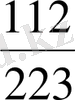 .
.
Шешуі.
А)
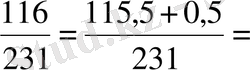
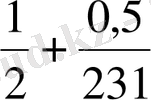 ,
,
В)

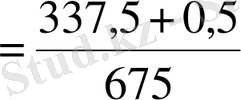
,
С)


,
D)
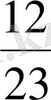
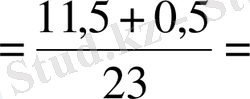
,
E)
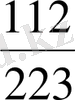
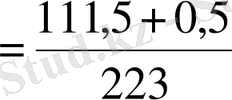
.
Бес қосындының бірінші қосылғыштары өзара тең, екінші қосылғыштарының алымдары бірдей, сондықтан қайсысының бөлімі кіші болса сол бөлшек үлкен болады. Сонымен, есептің жауабы:
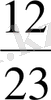 .
.
Жауабы.
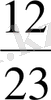 .
.
15 . Төмендегі сандардың ішінен ең үлкенін табыңыз:
А)
 . В)
. В)
 . С)
. С)
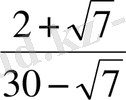 . D)
. D)
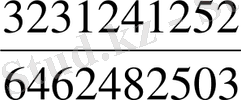 .
.
E)
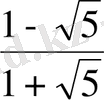 .
.
Шешуі.
А)


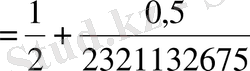 ,
,
В)

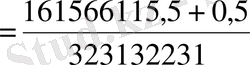
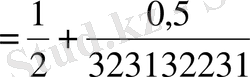 ,
,
С)
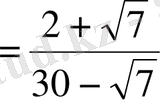
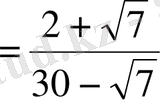

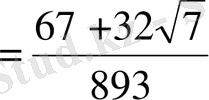

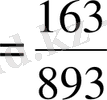
 ,
,
D)
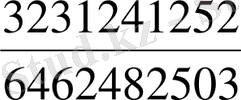
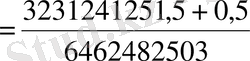
 ,
,
E)
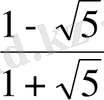
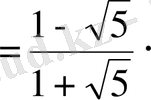
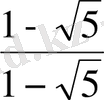
 .
.
Жауабы.
 .
.
16
. Төмендегі сандардың ішінен ең үлкенін табыңыз. А)
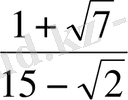 .
.
В)
 . С)
. С)
 . D)
. D)
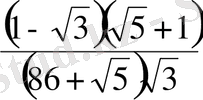 . E)
. E)
 .
.
Шешуі.
А)

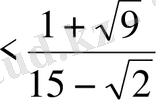
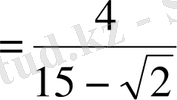
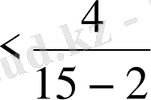
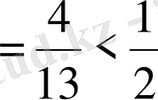 ,
,
В)

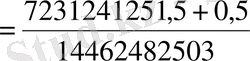
 ,
,
С)

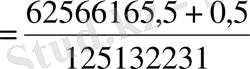
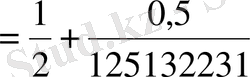 ,
,
D)
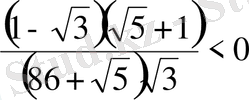 ,
,
E)


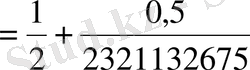 .
.
Жауабы.
 .
.
17
.
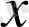 пен
пен
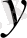
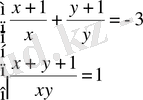 жүйесінің шешімі болса,
жүйесінің шешімі болса,
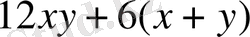 неге тең?
неге тең?
Шешуі.
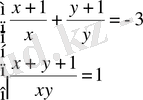
 (жүйенің екі теңдеуін де түрлендіреміз)
(жүйенің екі теңдеуін де түрлендіреміз)

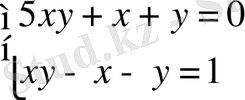
 (жүйенің екі теңдеуін мүшелеп қосамыз және 1-ші теңдеуден 5 еселенген 2-ші теңдеуді мүшелеп азайтамыз)
(жүйенің екі теңдеуін мүшелеп қосамыз және 1-ші теңдеуден 5 еселенген 2-ші теңдеуді мүшелеп азайтамыз)

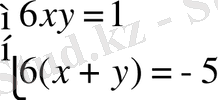

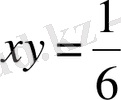 ,
,
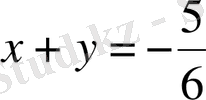 .
.
Онда
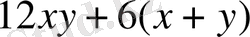

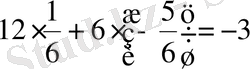 .
.
Жауабы.
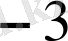 .
.
18
. Егер
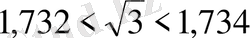 болса,
болса,
 теңдеуінің 0, 99 санына ең жақын орналасқанын табыңыз.
теңдеуінің 0, 99 санына ең жақын орналасқанын табыңыз.
Шешуі.
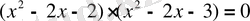
 (
(
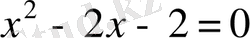 ,
,
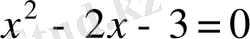 ) . 1-ші теңдеудің түбірлері
) . 1-ші теңдеудің түбірлері
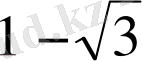 және
және
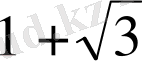 , 2-ші теңдеудің түбірлері
, 2-ші теңдеудің түбірлері
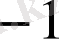 және
және
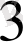 . Олардың ішінде 0, 99 санына ең жақын орналасқаны
. Олардың ішінде 0, 99 санына ең жақын орналасқаны
 .
.
Жауабы.
 .
.
19
. Егер
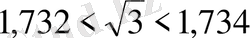 болса,
болса,
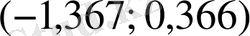 интервалында
интервалында
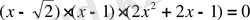 теңдеуінің неше түбірі болады?
теңдеуінің неше түбірі болады?
Шешуі.
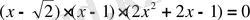
 (
(
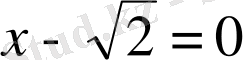 ,
,
 ,
,
 ) . 1-ші теңдеудің түбірі
) . 1-ші теңдеудің түбірі
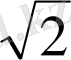 , 2-ші теңдеудің түбірі
, 2-ші теңдеудің түбірі
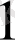 , 3-ші теңдеудің түбірлері
, 3-ші теңдеудің түбірлері
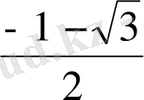 және
және
 . Олардың ішінде
. Олардың ішінде
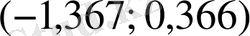 интервалына тиістісі
интервалына тиістісі
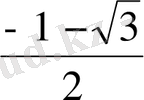 ғана.
ғана.
Жауабы. Бір.
20
. Егер
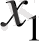 ,
,
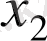
 теңдеуінің әртүрлі екі түбірі болса,
теңдеуінің әртүрлі екі түбірі болса,
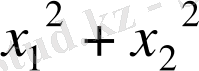 неге тең?
неге тең?
Шешуі.
Әрине, теңдеудің түбірлерін өзімізге белгілі тәсілмен тауып алып, ізделінді шаманы есептеуге болады. Берілген теңдеуді
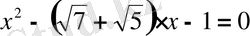 түрінде көшіріп жазып, Виет теоремасын қолдансақ есеп оңай шығады:
түрінде көшіріп жазып, Виет теоремасын қолдансақ есеп оңай шығады:
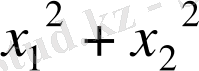

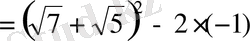
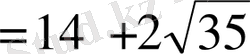
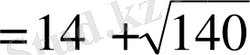 .
.
Жауабы.
 .
.
21
. Егер
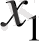 ,
,
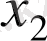
 теңдеуінің әртүрлі екі түбірі болса,
теңдеуінің әртүрлі екі түбірі болса,
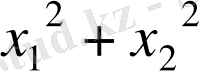 неге тең?
неге тең?
Шешуі.
Жоғарыдағыдай, берілген теңдеуді
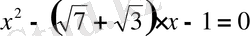 түрінде көшіріп жазып, Виет теоремасын қолданамыз:
түрінде көшіріп жазып, Виет теоремасын қолданамыз:
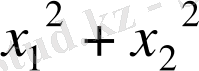

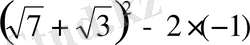
 .
.
Жауабы.
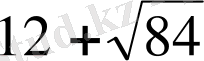 .
.
22
.
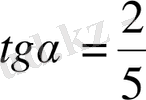 болса,
болса,
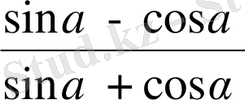 неге тең?
неге тең?
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz