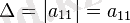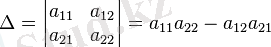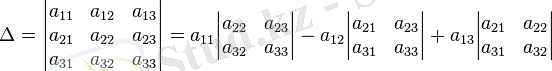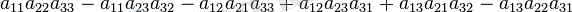Матрица, анықтауыш, векторлар

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым Министрлігі

Семей қаласының Шәкәрім атындағы Мемлекеттік университеті

СӨЖ

Тақырыбы: Матрица, анықтауыш, векторлар.

Орындаған: Нургазина Г

Тексерген: Джунусова М. Ж .

2015 жыл

Жоспар:

Матрица
Анықтауыштар
Векторлар

Матрица

Матрица теориясының негізін 19 ғ-дың 2-жартысы мен 20 ғ-дың басында К. Вейерштрасс (1815 - 1897) пен неміс математигі Ф. Фробениус (1849 - 1917) қалаған. Математикада кез келген жиынның элементтерінен құрылған және m жол мен n бағаннан тұратын тік төртбұрышты А кестесі. Матрицаны түзетін нысандар оның элементтері деп аталады. Матрицаның элементтері оның жолдары немесе бағаналарының бойымен орналасады. Матрицаның элементтері а _іj түрінде қос индекспен өрнектеледі, мұндағы бірінші индекс і - Матрицаның аіj элементі орналасқан жолының нөмірін, екінші индекс j - оның аіj элементі орналасқан бағананың нөмірін көрсетеді. Матрица символдық түрде не дөңгелек жақша, не қос тік сызық арқылы өрнектеледі. Мұндай матрицаны (m n) өлшемді тікбұрышты матрица деп, ал егер m=n болса, квадрат матрица деп, n санын оның реті деп атайды. Матрицаны қысқаша былай белгілейді: (а _іj ) .

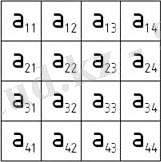
Егер барлық (а _і =а) болса, онда скаляр матрица шығады. Барлық элементтері нөлге тең М. нөлдік М. деп аталады. Жолдары мен бағаналарын ауыстыру арқылы алынған матрица транспозицияланған матрица деп аталып, А немесе АТ арқылы белгіленеді. Матрицаға қосу, көбейту алгебралық амалдар қолданылады. А тікбұрышты (m n) матрицасының санына көбейтіндісі деп барлық аіj элементтерін санына көбейткенде шығатын матрицаны айтады: . Бұл амалдар: А+В=В+А, А+(В+С) =(А+В) +С, ( + ) А= = А+ А, (А+В) = А+ В, ( А) =( ) А қасиеттерін қанағаттандырады. Матрицаның қосындысы оның құрау-шыларының қосындысына тең. Матрицаны көбейту амалы 1-көбейткіш бағаналарының саны 2-көбейткіш жолдарының санына тең тік бұрышты матрицалар үшін ғана орындалады. (m p) өлшемді А матрицаның (p n) өлшемді В матрицасына көбейтіндісі элементтері с _іj =а _і1 b _1j +а _і2 b _2j + +…+а _іp b _pj , і=1, …, m, j=1, …, n болатын (m n) өлшемді C матрицасы болып табылады. Матрицаларға енгізілген үш амал сандарға қолданылатын амалға жақын. АВ және ВА матрицаларының көбейтіндісі бірінші ретті квадрат М. үшін ғана анықталады және көбейткіштердің ретіне де байланысты, яғни АВ=ВА орындалмай қалуы да мүмкін. Егер АВ=ВА болса, онда А және В матрицалары ауыспалы деп аталады. Әрбір көбейткіші нөлден өзгеше болса да, екі матрицаның көбейтіндісі нөлдік матрицаға тең болуы мүмкін. Сонда М. үшін (АВ) =А В, , (AB) *= =В*А* ережелері орындалады.

Анықтауыштар

Анықтауыш (немесе детермина́нт) - сызықтық алгебраның негізгі ұғымдарының бірі. Квадрат матрицаның анықтауышы оның элементтеріне қатысты көпмүшелікті айтады. Жалпы жағдайда матрицалар кез келген коммутативті сақинада анықталады, бұл кезде анықтауыштары да осы сақина элементі болады.

А матрица анықтауышы - det(A) , А немесе Δ(A) деп белгіленеді.

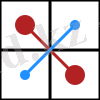
Бірінші дәрежелі детерминант осы матрицаның жалғыз элементінің өзі болып табылады:

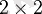матрица үшін детерминанты былай анықталады

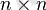матрица үшін анықтауышы рекурсивті анықталады:

, где - элементінің қосымша миноры. Бұл формула қатар бойынша жіктелуі деп аталады.

Соның ішінде, 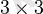матрица детерминанты былай есептеледі:

Векторлар

Вектор деп бағытталған кесіндіні айтады, яғни кесіндінің белгілі бір ұзындығы және бағыты болады. Егер А - вектордың басы, ал В -вектордың ұшы болса, онда вектор 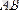немесе символымен белгіленеді. 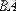векторы 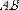векторына қарама-қарсы вектор деп аталады (оның басы В нүктесінде, ал ұшы А нүктесінде орналасқан) . векторына қарама-қарсы векторды деп белгілейді. векторының ұзындығы немесе модулі деп 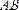кесіндісінің ұзындығын айтады және оны 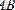немесе деп белгілейді. Ұзындығы нөлге тең векторды нөлдік вектор деп атайды және ол деп белгіленеді. Нөлдік вектордың бағыты анықталмаған. Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны деп белгілейді. Егер бірлік вектордың бағыты векторының бағытымен сәйкес келсе, онда ол векторының орты деп аталады және деп белгіленеді.