Резерфорд тәжірибелері, де Бройль гипотезасы және кванттық механиканың негізгі ұғымдары


Семей қаласының Шәкәрім атындағы мемлекеттік университеті
СӨЖ
Тақырыбы: Резерфорд тәжірибелері. Ритцтің комбинациялық принципі. Бор-Зоммерфольдтің квантталу ережелері.
Орындаған: Сартбаева Т. Қ
Тобы: Т-323
Тексерген: Мешетова Ж. С
Семей 2015
Электрондар дифракциясы. Де Бройль гипотезасы
Жарық табиғаты туралы түсінігінің дамуы нәтижесінде оптикалық құбылыстарда өзіндік дуализм байқалатыны анықталды. Жарықтың осындай толқындық табиғатын (интерфернция, дифракция) дәлелдейтін қасиеттерімен қатар басқа да жарықтың корпускулалық табиғатын (фотоэффект, Комптон көрінісі) көрсететін қасиеттер бар.
Шешудің дұрыс жолын 1924 жылы де Бройль тапты. 1922-1923 жж. Иоффе мен Комптонның тәжірибелері Эйнштейннің корпускулалық-толқындық сәуле шығару табиғатының екі жақтылығы туралы ойының дұрыстығын растады. Де Бройль электронның, кейін басқа да бөлшектердің табиғатының сондай екі жақтылық туралы ойын ұсынды. Бұл дегеніміз фотон қозғалысы секілді электрон қозғалысымен толқындық процесті қою керек. Электронға қандай толқынды сәйкестендіру қажет?
Де Бройль фотонның қасиеттерінің арасындағы байланыс электронның корпускулалық және толқындық қасиеттері арасында да бар деп тұжырымдады. Фотон энергияға
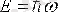
және импульсқа ие
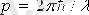
немесе
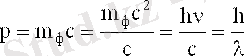
Де Бройльдің ойынша электронның немесе қандай да бір басқа бөлшектің қозғалысы толқындық процеспен байланысты. Толқын ұзындығы тең:
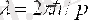
Немесе:
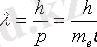
ал жиілігі
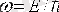
Релятивситтік емес бөлік үшін (яғни, с-дан аз жылдамдықпен қозғалатын бөлік) (2. 4) формуласы мына түрде жазылады:
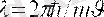
Электронның 10 4 В аспайтын потенциалдар айырымы U электрлік поледа жылдамдауы нәтижесінде, электрон массасы m e тыныштық массасынан m 0e ерекшеленбейді. Электронның жылдамдау поледа тудыратын кинетикалық энергия мынаған тең:
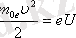
және жылдамдық
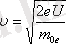
(2. 6) мен (2. 7) өрнегінен (U киловольтқа өте) :
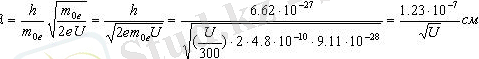
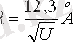
Қарапайым электрондық құрылғыларда жылдамдататын полялар 1÷10 4 В аралығында жатады. Ұшқан электрондардың сәйкес толқын ұзындықтары 10÷0, 1Å құрайды, яғни қарапайым рентген сәулелерінің толқын ұзындықтары аралығында өзгереді. Электрон құрылғысы l ≈ 10см өлшемінде болғанда, яғни λ<<ℓ, электрондық шоғыр үшін толқындық қасиеттер байқалмайды. Толқындық қасиеттер, әсіресе электрондар дифракциясы дифракциялық торда тұрақты ~λ-мен байқалуы мүмкін. Рентген сәулелері үшін секілді электрондар дифракциясын табиғи-кристалдық-тордың көмегімен тауып көруге болады. Бұндай тәжірибелерді 1927 ж. Дэвинсон мен Джермер орнатқан (2. 1 сурет) .
Монохромат электрондардың шоғыры электрондық пушкадан рентгенстуктуралық анализдің берілгенінен стуктурасы жақсы белгілі никель кристалының бетіне түсті. Кристалдан шашыраған электрондар сезімтал гальванометрге жалғанған арнайы электродтармен екіге жіктелді. Электрон қабылдағышы түрлі бұрыштардан шашырайтын электрондарды қабылдай алатындай қозғала алды. Электрон энергиясы 54 эВ болғанда Вульф-Брэгг формуласына 2dsinυ=λ толқын ұзындығына 1, 67Å сәйкес келетін шағылу бұрышы үшін υ=50° максимум пайда болды. Тағы теңдіктен:
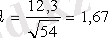 Å.
Å.
Нәтижесі де Бройль ойының дұрыстығының керемет дәлелі болып табылады. Де Бройльдің формуласы сан рет тексерілгенде теория мен тәжірибе бірімен-бірі сәйкес келетін. Осылай совет үкіметінің ғалымы П. С. Тартаковский тез электрондардың жұқа металдық пленкадан өтуін зерттеді. Зерттеулер келесі ретпен орындалды (2. 2 сурет) . Потенциалдар айырымы бірнеше ондық киловольтке жылдамдатылған электрондар шоғыры жұқа металдық фольгадан өтіп, фотопластинкаға түсті. Электрон фотопластинкаға соқтығысқанда оған фотон сияқты әсер етеді. Сонда рентген сәулелерінің кристал ұнтақтардан өткендегі сияқты дифракциялық көрініс пайда болады. Бұл осындай пленкаларда микрокристалдық структура бар екенін көрсетеді.

2. 1 - Сурет - Электрондар дифракциясын зерттеу
Сонымен, электрондар фотондар сияқты корпускулалық қасиеттермен қатар толқындық қасиеттерге ие. Электрон табиғатының бұл екі жақтарының қатынасы жайлы өзіне айқын есеп беру керек.
Толқындық қасиет тек электрондардың үлкен жиынтығының ағынына ғана тән емес пе? Бұндай тұжырым фотондарға айтылған, бірақ С. И. Вавиловтың, Яноштің және т. б. жұмыстарында теріске шығарылған. Электрондар үшін ұқсас тапсырма В. Фабрикантпен және оның жұмыскерлерімен шешілген болатын.
1948 ж. В. Фабрикант, Л. Биберман мен Н. Сушкин әр электрон құрылғыдан басқаларына тәуелсіз өтетіндей тоқ күші өте аз құрылғыда электрондар дифракциясымен тәжірибені іске асырды. Екі электрондардың құрылғыдан өтуінің орташа уақыты электронның құрылғыдан өту уақытынан шамамен 3 есе асты. Ұзақ экспозиция нәтижесінде тығыздығы үлкен электрон ағынының қысқа экспозициядағыдай дифракциялық көрініс пайда болды. Бұл тәжірибе толқындық қасиет әр электронға бөлек тән екенін көрсетеді.
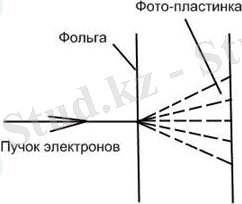
2. 2 - Сурет - Зерттеу жұмыстын өту реті
Фотондарда секілді бір электрон дифракциясы электрондар ағынының дифракциясы нәтижесінде пайда болатын нүктелердің бүкіл жүйесін бермейді. Дифракциялық тор - кристалды өткен бір электронның ізі дифракцияның жағдайымен шешілетін тек бір нүктеде орналасады. Осымен электрон табиғатының корпускулалық жағы байқалады - ол дифракция жағдайын қанағаттандыратын барлық бағытта «шашырай» алмайды, оның әрекеті тек бір жерде көрінеді. Бұл әрекет мүмкін болатын қай бағытта байқалатынын айтуға болмайды. Заманауи теория электрон әрекеті пластинаның қай нүктеде байқалу ықтималдығын есептеуге ғана мүмкіндік береді. Бұл электрондардың үлкен жиынтығының өтуін айтарлықтай дәл ойлауды мүмкін етеді.
Осындай әдіспен біз электрон табиғатының келесі қорытындысына тоқталамыз:
1. Электрондар дифракцияны анықтағанда көрінетін электронның толқындық табиғаты электронды «материалық нүкте»-кішкентай бөлшек, корпускула ретінде елестетуге мүмкін еместігін дәлелдейді. Электрон күрделі материалды зат, толқындық қасиеттерге ие күрделі стуктура болып табылады. Бұл структура электронның жағдайына байланысты өзгереді, яғни оның қоршаған материямен қатынасың қасиетіне байланысты. Осылай электрон атомда ішінде болғанда немесе бір уақытта тордың мыңдаған атомымен байланысып кристалды өткенде электрон локализациясы (яғни де Бройль толқынының амплипудасы нөлден ерекше болғандағы аймақта) әр түрлі болатыны анық. Кеңістікті тордағы электрондар дифракциясы 2. 3 (а) суретінде көрсетілген. Дифракциялық максимумы электронның торды өткенде бір уақытта көптеген атомдармен әрекеттесетінін дәлелдейді (2. 3 (б) сурет) ;
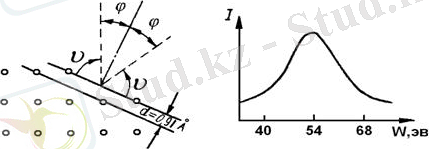
а) б)
2. 3 - Сурет - Кристаллдық тордағы дифракция
2. Электрон әрқашан бөлшектерге бөлінбей бір бүтін ретінде әрекет еткенде электрон табиғатының корпускулалық жағы байқалады. Оның бөлінбеуі оның «нүктелігімен» шарттанбайды (өйткені ол материалық нүкте емес), бірақ ол болашақта ғана шешілетін тым күрделірек табиғатқа ие.
Әлі күнге дейін корпускулалық және толқындық аспекттердің қатынас табиғаты түсінігінің бір де көзқарасы жоқ. Бұл мәселені қарастыру физиканың жалпы курсынан тыс. Жоғарыда айтылғандар корпускулалық-толқындық қасиеттердің бар болуы сипаттама статикасына, электронның әрекетін тек ықтималдықпен ойластыру мүмкіндігіне әкеледі. Де Бройль толқыны материалық бөлшек қозғалысын сипаттайды, бірақ ол «структуралық» бөлшек деп нені айту керек екені туралы ешқандай мәлімет бермейтінін есте сақтау керек. Электрондар структурасын білу (басқа бөліктер сияқты) зарядтар ұқсастығы, тыныштық, спин массалары, өзіне ұқсас бөлшектер мен өзге табиғат бөлшектерімен қатынасының қасиеті және т. б. түсіндіруі керек.
Физикалық шамалардың операторлары жайындағы түсінік
Оператор. 1926 ж. М. Борн, Н. Винер әрбір классикалық физикалық шамаға белгілі қасиеттерге ие, қайсыбір оператор салыстырылады деген идея ұсынды. Бұл қазір кванттық теория формализмінің негізі болып отыр.
Оператор-шартты белгі, немесе ереже; оны қолдану арқылы бір функциядан басқа функцияны алуға болады. Физикада операторлар әдетте үстіне ∃ таңбасын қойып белгіленеді:
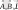 Егер
Егер
 операторы арқылы
ψ(х)
функциядан
ϕ(х)
функция алынатын болса, онда операторы
ψ(х)
функциясына әсер етеді (немесе операторы
ψ(х)
функциясын
ϕ(х)
-ға айналдырады) деп айтады. Оператордың осы амалы (әрекеті) былай жазылады:
операторы арқылы
ψ(х)
функциядан
ϕ(х)
функция алынатын болса, онда операторы
ψ(х)
функциясына әсер етеді (немесе операторы
ψ(х)
функциясын
ϕ(х)
-ға айналдырады) деп айтады. Оператордың осы амалы (әрекеті) былай жазылады:
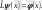 (4. 10)
(4. 10)
Мысалы,
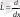 және
ψ(х) =sіnx
болсын дейік. Сонда
және
ψ(х) =sіnx
болсын дейік. Сонда
 яғни
яғни
 операторы
sinx
функциясын
cosx
функциясына айналдырады.
операторы
sinx
функциясын
cosx
функциясына айналдырады.
Кванттық механикада күйлердің суперпозиция принципі қанғат-тандырылуы үшін тек сызықтық операторлар қолданылады. Және кез келген сызықтық оператор емес, тек өзара түйіндес, немесе эрмиттік операторлар қолданылады.
Оператор қасиеттері. Операторлардың қосындысы да оператор болады. Демек
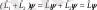 .
.
 және
және
 екі оператордың қосындысы және айырмасы былай анықталады:
екі оператордың қосындысы және айырмасы былай анықталады:
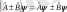 (4. 11)
(4. 11)
және операторларының көбейтіндісі
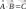 былайша анықталады:
былайша анықталады:
 .
(4. 12)
.
(4. 12)
 операторы
ψ
функциясына былай әсер етеді; алдымен
ψ
функциясына операторы әсер етіп, жаңа
ϕ
функциясы
ψ=ϕ
пайда болады да, бүған енді операторы әсер етеді
ϕ=⋅ψ
.
операторы
ψ
функциясына былай әсер етеді; алдымен
ψ
функциясына операторы әсер етіп, жаңа
ϕ
функциясы
ψ=ϕ
пайда болады да, бүған енді операторы әсер етеді
ϕ=⋅ψ
.
Егер
 (немесе
(немесе
 ) болса, онда және операторлары өзара коммутирленеді (бірімен-бірі орын алмастыра алады) ; егер болса, онда және операторлары өзара коммутирленбейді. Мысалы, және
х
операторлары коммутир-ленбейді.
) болса, онда және операторлары өзара коммутирленеді (бірімен-бірі орын алмастыра алады) ; егер болса, онда және операторлары өзара коммутирленбейді. Мысалы, және
х
операторлары коммутир-ленбейді.
-≡, айырмасы және операторларының коммутаторы деп аталады.
Егер оператор мына шарттарды
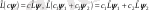 (4. 13)
(4. 13)
қанағаттандыратын болса, онда ол сызықтық деп аталады. Мұндағы с, с 1 , с 2 - кез келген тұрақтылар, ψ 1 , ψ 2 - кез келген функциялар.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz