Кванттық теориялардың негізгі тұжырымдары: Франк-Герц тәжірибелері


Қазақстан Республикасының Білім және Ғылым министірлігі Шәкәрім атындағы Семей мемлекеттік университеті
СӨЖ
Тақырыбы: Кванттық теориялардың негізгі ойларын тәжірибе жүзінде тұжырымдау. Франк және Герц тәжірибелері
Орындаған:Қапай. Г. Е
Топ:БЛ-409
Тексерген: Рахимбердина. А. Т
Семей 2015
Жоспар
- Кванттық теориялардың негізгі тұжырымдары
- Франк және Герц тәжірибелері
- Бордың постулаттары
Қорытынды
Пайдаланған әдебиеттер тізімі
Кванттық теориялардың негізгі ойларын тәжірибе жүзінде тұжырымдау. Франк және Герц тәжірибелері
Едәуір жоғары температураға дейінгі қыздырылған денелердің жарық шығара бастайтындығы практикада әрбір адамға белгілі. Мысалы, металдарды қыздырған кезде олар алғашқыда қоңыр қызыл түсті, артынан әрі қыздырудың барысында ашық қызыл түске ие болады, одан әрі қыздырғанда ақ шоқ деп аталатын түске келеді. Басқаша айтқанда қатты жєне сұйық денелер жоғары температураға дейін қыздыру кезінде спектрдің көрінетін аймағында сәулеленуге ие болады. Бұл кезде температураны өсіруге байланысты сәулеленудің интенсивтілігі жєне спектрлік құрамы өзгереді. Сәулеленуші дененің ішкі энергиясы есебінен пайда болатын жєне тек дененің температурасы мен химиялық қасиеттеріне байланысты электромагниттік сєулелену жылулық сәулелену деп аталады. Температуралық тепе-теңдікте тұрған денелердің жылулық сєулеленуі, сондай денеге түсетін сәулеленудің энергия мөлшерін жұтуымен теңестіріледі.
Дененің жылулық сәулеленуінің спектралды сипаттамасы үшін дененің сәуле ығарғаштық қабілеттілігі деген түсінік енгізіледі, оны сонымен қатар, шығарғыштық қабілеттілігі немесе энергетикалық жарқыраудың Е(ν, Т) спектралды тығыздығы деп атайды.
Денелердің сәуле шығарғыштык, қабілеттілігі деп уақыт бірлігі ішінде дене бетінің аудан бірлігіне келетін жиіліктері
\[\mathcal{V}\]-ден\[\mathcal{V}\]+ d\[\mathcal{V}\]аралығында шығарылатын электромагниттік сәулеленудің dW энергиясын айтады. Сонымен,Е(
\[\mathcal{V}\], Т) = dW сєу / d\[\mathcal{V}\](7. 1)
СИ жүйесінде, сєуле шығарғыштық қабілеттілігі Дж/м 2 пен өрнектеледі. Электромагниттік толқындар жұтылуының спектралды сипаттамасы үшін денелердің жұтылу қабілеттілігі үшін А(ν, Т) деген ұғым енгізіледі. Жұтылу қабілеттілігі, уақыт бірлігі ішінде дене бетінің аудан бірлігіне жиіліктері υ-ден υ + dυ аралығында түсетін dW энергиясының қандай бөлігін дене жұта алатындығын көрсетеді, яғни
А(ν, Т) = dW жұт /dW (7. 2)
Денелердің сәуле шығарғыштық жєне сәуле жұтқыштық қабілеттілігі, дененің температурасына, жиілігіне, дененің химиялық құрамына жєне дене бетінің күйіне байланысты болады. Егер кез-келген температурада және барлық жиіліктер үшін А(ν, Т) = 1 болса, онда дене абсолют қара дене деп аталады. Абсолют қара дененің сәуле шығарғыштық қабілеттілігін ε(ν, Т) деп белгілейміз. Ол дененің сәулелену жиілігіне жєне абсолют температурасына тєуелді. Абсолют қара дене єдетте физикалық үлгі ретінде алынады, бірақ табиғатта көптеген денелер өзінің қасиеттері бойынша абсолют қара денелерге жақын келеді. Мысалы құрым, қара елтірі, қара бархыт. Абсолют қара дененің идеалды үлгісі ретінде мөлдір емес қуыс бетіндегі кішкене тесікті алуға болады (7. 1-сурет)
\[\bigotimes_{\mathbb{Q}}^{\ n}\]7. 1-сурет
Кішкене тесік арқылы қуыс ішіне түсетін жарық сәулесі қуыс қабырғаларына көп ретті шағылуға кездеседі. Әрбір шағылу кезінде жарық толқыны энергиясының кейбір бөлігі жұтылатын болады. Сондықтан, тесіктен шығатын сәуленің интенсивтілігі, оған келіп түскен сәуле энергиясына қарағанда көп шамаға азаяды. Қуыс бетінің ауданының тесік бетінің ауданына қатынасы үлкен болған сайын, тесік беті өзінің қасиеті бойынша абсолют қара денеге соншама жақын келеді. Реал денелердің сипаттамасы үшін көп жағдайда сұр дененің үлгісі пайдаланылады. Дене сұр деп аталады, егер де оның жұтылу қабілеттілігі барлық жиіліктер үшін бірдей болса, жєне ол тек температура мен дене бетінің күйіне тәуелді болса, яғни А сұр (ν, Т) = А(Т) . Денелердің сәуле шығарғыштық жєне сәуле жұтқыштық қабілеттіліктері бір-бірімен байланысты. Бұл байланыстарды тағайындау үшін, екі шексіз ұзын а және в пластинкалардан құралған (7. 2-сурет) жылу өткізбейтін (адиабаттық)
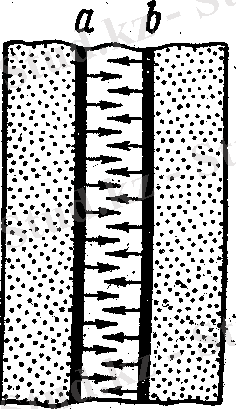
7. 2-сурет
жүйені қарастырамыз, тек пластинкалар ғана бір-бірімен жылу алмаса алады. Пластинканың а беті абсолют қара. Термодинамикалық тепе-тендік күйінде екі пластинканың температурасы да бірдей және сєулелену тепе-тендік күйде болады. Сєуле шығарғыштық және сәуле жұтқыштық анықтамасы бойынша екі пластинка үшін былай жазуға болады:
dW шығ = E(ν, Т) dν
dW жұт = А(ν, Т) dW (7. 3)
Термодинамикалық тепе-теңдік күйінде
dW= dW шығ
Абсолют қара а пластинкасы үшін

dW шығ = ε(ν, Т) dν (7. 4)
а пластинкасы энергияны шағылдырмай толық жұтатындықтан бұл пластинканың сєулелену энергиясы пластинкаға келіп түскен энергияға тең болады: dW шығ =dW. Сондықтан (7. 3) өрнегінен алатынымыз:
dW жұт = А(ν, Т) ε(ν, Т) dν
Термодинамикалық тепе-теңдік күйінде dW шығ =dW жұт , олай болса
E(ν, Т) dν= А(ν, Т) ε(ν, Т) dν
немесе E(ν, Т) / А(ν, Т) = ε(ν, Т) (7. 5)
Сонымен, дененің сәуле шығарғыштық қабілеттілігінің оның жұтқыштық қабілеттілігіне қатынасы дененің химиялық құрамына тєуелді болмайды жєне ол абсолют қара дененің сєуле шығарғыштық қабілеттілігі болып, ол температура мен жиіліктің f(ν, Т) функциясы болып табылады. Бұл заңды бірінші рет Кирхгоф тағайындады, сондықтан заң соның атына берілді, ал f(ν, Т) функциясы Кирхгоф функциясы деп аталады. Кирхгоф заңынан A(ν, Т) = 1, онда Е(ν, Т) = ε(ν, Т), егер А(ν, Т) = 0 болса, онда ε(ν, Т) = 0 болады. Сондықтан, егер дене берілген температурада берілген жиіліктер аралығында жұтпайтын болса, онда ол бұл температура да және бұл жиіліктер аралығында да сєуле шығармайды, яғни сєулеленбейді.
0-ден
\[\infty\]-ке дейінгі жиіліктегі барлық спектр бойынша толық сәулелену қуаты дененің энергетикалық жарқырауы немесе интегралды сәуле шығарғыштық қабілеттілігі Е(Т) деп аталады. Анықтама бойынша, ол мынаған тең:Е(Т) =
\[\stackrel{\vec{v}}{}\!\!\langle n,T\rangle d\nu\]
немесе Кирхгоф заңын есепке алсақ, онда
Е(Т) =
\[{}^{\circ}\S(n,\mathrm{T})\,e(n,T)d\nu\](7. 6)
Абсолют қара дене үшін A(ν, Т) = 1, сондықтан
Е(Т) =
\[\stackrel{\vec{v}}{}\!\!\langle n,T\rangle d\nu\](7. 7)
Бұдан әрі жылулық сәулелену теориясының негізгі мєселесі Кирхгоф функциясының ашық түрін іздеу болып табылады. 1879 жылы Д. Стефан тєжірибелік мєліметтерді талдау негізінде төмендегідей қорытындыға келді: кез-келген дененің энергетикалық жарқырауы абсолют температураның төрт дәрежесіне пропорционал болады. Бірақ Л. Больцман 1884 жылы термодинамикалық єдіспен теориялық бұл пікірдің тек абсолют қара дене үшін дұрыс болатындығын көрсетті. Сондықтан, бұл тєуелділік физика тарихында Стефан-Больцман заңы деп аталады.
ε(Т) =σ-Т 5 (7. 8)
яғни, абсолют қара дененің энергетикалық жарқырауы абсолют температуранық төрт дәрежесіне тура пропорционал. σ=5, 67-10 8 (Вт/м 2 к 4 ) - пропорционалдық коэффициенті Стефан-Больцман заңының тұрақтысы деп аталады. Бірақ, олар Кирхгоф функциясының ашық түрін шешкен жоқ. Кирхгоф функциясының ашық түрін ашудағы алғашқы қадамды 1893 жылы В. Вин жасады. Ол, жылжып айналатын поршені бар және айналы қабырғалары бар цилиндрлік ыдыста абсолют қара дененің адиабатты сығу сәулеленуі туралы есепті қарастырды. Осының нєтижесінде ол Кирхгоф функциясы үшін келесі өрнекті алды:
ε(ν, Т) =f(ν, Т) = V 3 f(ν, Т) (7. 9)
мұндағы
\[\textstyle{\mathcal{F}}\](\[\boldsymbol{\nu}\], Т) - кейбір белгісіз ашық түрдегі функция. В. Вин\[\textstyle{\mathcal{F}}\](\[\boldsymbol{\nu}\]/Т) функциясының ашық түрін тағайындамаса да, бірақ (7. 9) В. Вин өрнегінен Стефан-Больцман заңы шығады.Абсолют қара дененің сәуле шығарғыштық қабілеттілігінің әртүрлі температурадағы жиіліктен тєуелділігі 7. 3-суретте көрсетілген түрде болатындығы тєжірибелерден белгілі.
8. 1. Франк және Герц тәжірибелері.
Классикалық физика заңдарына құрылған планетаарлық жүйе болып табылатын және бөлшектерінің шашырауы бойынша жүргізілген тәжірибелердің нәтижелерін талдауға негізделген Резерфордтың атомдық моделі эксперименталды фактілермен толық қарама-қарсы қайшылықта болды. Біріншіден, классикалық теорияға сәйкес, электрон ядроның айналасында дөңгелектік орбита бойынша қозғала отырып, үздіксіз сәуле шығаруға тиіс. Шындығында, атом тек кейбір шарттар негізінде ғана сәулеленеді. Екіншіден, Резерфордтың атомдық моделі тұрақсыз болды, бірақ шындығында атом тұрақты жүйе болып табылады. Үшіншіден, Резерфорд моделіндегі атомның сәулелену спектрі үздіксіз (тұтас) болуы керек, ал тәжірибеде атомның сәулеленуі сызықтық спектр болып табылады. Бұл деген сөз, классикалық физика заңдарын атом теориясына біркелкі қолдану тәжірибелік фактілермен қарама-қарсы қайшылықта болуға әкелді.
Алдымен, атомдардың сәулеленуінің кейбір заңдылықтарын қарастырайық. Жарқырауық газдар сәулеленудің сызықтық спектрлерін беретіндігі белгілі. 1885 жылы И. Бальмер сутегі атомы спектрінің көрінетін бөлігінің тоғызыншы сызығының толқындық ұзындығын
өрнегімен сипаттауға мүмкін болатынын тағайындады. Мұндағы
Бальмер өрнегін сәулеленудің жиілігі үшін мына түрде жазуға болады.
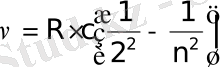 (8. 2)
(8. 2)
толқын ұзындығы мен жиілік арасындағы
қатынасын қанағаттандырады, мұндағы n 1 және n 2 - кейбір бүтін сандар. Т(n 1 ) және Т(n 2 ) функциялары спектралды термдер деп аталады. (8. 2) және (8. 3) өрнектерін салыстыра келіп
болатындығы шығады. 1908 жылы В. Ритц, кез-келген атомның сәулеленуінің спектралды сызықтарының жиілігі екі терм айырымы түрінде беруге болатындығын тағайындады; термдердің әртүрлі комбинацияларын құрай отырып, бұл атомның спектралды сызықтарының мүмкін болатын барлық жиілігін табуға болады. Мұндай ұйғарым Ритцтің комбинациялық принципі деген атқа ие болды. Ритцтің комбинациялық принципін қолданып, сутегі атомы сәулелену сызықтарының толқын ұзындығын есептеуге мүмкін болатын сериалды өрнектерді алуға болады.
Спектрдің алыс ультракүлгін аймағын бақылайтын Лайман сериясы мынадай өрнек арқылы сипатталады:
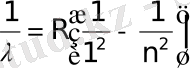 , (8. 4)
, (8. 4)
мұндағы n=2, 3, 4, … Сутегі атомы спектрінің көрінетін аумағында бақыланатын Бальмер сериясы келесі өрнекпен сипатталады
мұндағы n=3, 4, 5, …
Спектрдің инфрақызыл аумағында бақыланатын Пашен сериясы мына өрнек бойынша сипатталады
мұндағы n=4, 5, 6, …
Сонымен бірге, алыс инфрақызыл аймағында келесі сериялар байқалған:
Брэкет сериясы
\[{\frac{1}{\lambda}}=\mathbb{R}{\frac{1}{\lambda^{2}}}\cdot{\frac{1}{\Omega^{2}}}\delta\](8. 7)
мұндағы n=5, 6, 7, …
Пфунд сериясы
мұндағы n=6, 7, 8, …
Хэмфри сериясы
мұндағы n=7, 8, 9, …
Атомның классикалық емес теориясын құрудың алғашқы талпынысын 1913 жылы дат физигі Н. Бор жасаған. Бірақ Бордың теориясында Резерфорд моделінің көзқарасынан алшақ кетпеушілік байқалады. Бірақ атомдағы электронның күйіне арнайы шектеулер енгізді. Атом моделі Бор тағайындаған постулаттарға құрылды.
Бордың бірінші постулаты : атом, кейбір стационар күйлерде, өзінен энергия шығармайды және энергияны жұтпайды.
Бордың екінші постулаты : бір стационар күйден екінші стационар күйге көшкенде атом бір квант энергиясын шығарады немесе жұтады. Бұл постулат жиіліктер ережесі болып табылады және оны келесі түрде өрнектеуге болады: атом бір стационар күйден екінші стационар күйге көшкенде, стационар күйлердің энергиялар айырымына тең болатын һ квант энергиясын шығарады немесе жұтады, яғни
Бордың үшінші постулаты : атомның стационар күйіндегі электрон, импульс моменті Планк тұрақтысына еселік болатын дөңгелектік орбита бойынша қозғалады, яғни мына шартты қанағаттандырады:
мұндағы m - электрон массасы,
n=1 сәйкес мәніне тең күй - негізгі күй деп аталады, ал n>1 барлық басқа күйлер қозған күйлер деп аталады. Бор постулаттары сутегі атомының стационар күйлерінің энергияларын есептеуге мүмкіндік береді, бұл кезде Бордың есептеуі бойынша, сутегі атомындағы электрон, электронның ядроға кулондық тартылыс күш әсерінен классикалық заң бойынша дөңгелектік орбита бойымен қозғалады. Сутегі атомындағы электрон үшін Ньютонның екінші заңын жазып, мынаны аламыз:
Соңғы өрнектен электрон орбитасының r радиусын анықтаймыз
Электрон орбитасының радиусы үшін (8. 22) өрнегін (8. 20) өрнегіне қойып, түрлендіруден кейін n орбитасындағы электронның жылдамдығын табуға болады
(8. 22) пен (8. 23) -тен сутегі атомындағы электронның n-ші орбитасының радиусы:
Соңғы теңдеуден, орбита радиусы бүтін сан квадратына пропорционал түрде өсетіндігі көрінеді. Сутегі атомындағы электронның толық энергиясы оның кинетикалық және
8. 1-сурет
потенциалық энергияларының қосындысынан тұрады. Электронның кинетикалық энергиясы мына өрнек бойынша анықталады:
Сутегі атомындағы электронның потенциалық энергиясы мынаған тең:
Сутегі атомындағы электронның толық энергиясы
Сонымен, сутегі атомы туралы Бор көзқарасы атомның мөлшерін дәл анықтауға мүмкіндік берді. n=1 кезінде
Бұл шаманы сутегі атомының бірінші радиусы деп атайды (немесе бірінші бор орбитасының радиусы) . Сутегі атомындағы электронның толық энергиясы теріс шама болғандықтан, ол бас кванттық санның (n) артуына байланысты артады және n кезінде, Е0 болады. Енді сутегі атомының спектральды сәуле шығару сызықтарының пайда болуы 8. 1 - суретте көрнекті түрде талқылануы алынған (8. 1-сурет) .

Атомдардағы стационарлық күйлердің пайда болуы туралы Бор постулаттары және жиіліктердің ережесі 1913 жылы Д. Франк пен Г. Герцтің тәжірибелерінде өзінің орнын тапты. Тәжірибелік қондырғының сұлбасы 8. 2-суретте көрсетілген.
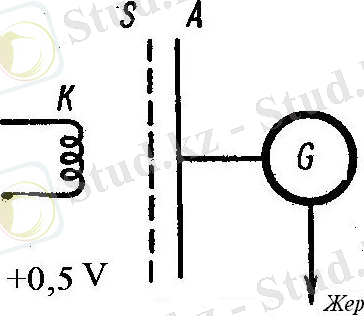
8. 2-сурет
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz