Салмақты функция: импульсті-өтпелі сипаттама, беріліс функциясы және өтпелі процестерді бағалау


Қазақстан Республикасы білім және ғылым министірлігі
Семей қаласының Шәкәрім атындағы мемлекеттік университеті
«Автоматика және элекротехника» кафедрасы
СӨЖ
Тақырыбы: Салмақты функция.
Орындаған: Кусманов А.
Тобы: АУ-301
Тексерген: аға оқытушы Секербаева А. Б.
Семей 2015 ж.
Мазмұны:
1 Негізгі бөлім . . . 2
1. 1. Импульсті-өтпелі функция (ИӨФ) немесе салмақты функция . . . 2
1. 2. Өтпелі процесті салмақ функциясы арқылы бағалау . . . 3
Қорытынды. . 5
Әдебиеттер. . . ……6
Негізгі бөлім
Салмақты функция деп -
 нөлдiк алғашқы шарттар кезiндегi бiрлiк шексiз импульсқа жүйенiң реакциясы ататлады (дельта-функция немесе Дирак функциясы) . Дельта-функция
нөлдiк алғашқы шарттар кезiндегi бiрлiк шексiз импульсқа жүйенiң реакциясы ататлады (дельта-функция немесе Дирак функциясы) . Дельта-функция
 мына теңдiктермен анықталады
мына теңдiктермен анықталады
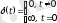 ,
,
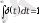 .
.
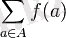
Дельта-функцияны
 нүктедегi центрi бар бiрлiктiк алаңның тiкбұрышты импульсiнiң шегi ретiнде қарастыруға болады.
нүктедегi центрi бар бiрлiктiк алаңның тiкбұрышты импульсiнiң шегi ретiнде қарастыруға болады.
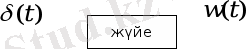
Екiншi атау - салмақтық функция -
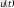 кiрiстiк сигнал үшiн жүйенiң
кiрiстiк сигнал үшiн жүйенiң
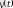 шығысы төмендегiдей есептелетiнмен байланысты
шығысы төмендегiдей есептелетiнмен байланысты
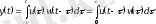 .
.
Мұнда
 функциясы кiрiстiк сигналды интеграластылық түсiнiкте «өлшейдi» .
функциясы кiрiстiк сигналды интеграластылық түсiнiкте «өлшейдi» .
1. 1.
Импульсті-өтпелі функция (ИӨФ) немесе салмақты функция
Импульсті-өтпелі функция (ИӨФ) немесе салмақты функция:
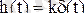 T
T
 h
h
Импульстiк сипаттама кiрiс шығыстық қатынастарды тек
нөлдiк алғашқы шарттарда
ғана көрсетедi, яғни жүйенiң динамикасын толығымен сипаттай алмайды.
Импульстi сипаттама түсiнiгi берiлiстiк функциясы
қатаң дұрыс
болатын жүйелер үшiн қолданады. Егер берiлiстiк функция дұрыс, бiрақ қатаң дұрыс емес болса, онда кiрiстен шығысқа тiкелей берiлiс коэффициентi нөлге тең емес, сондықтан кiрiстегi
 сәттегi шексiз импульс шығысқа берiледi. Мұндай импульстi сипаттаманы тұрғызу мүмкiн емес. . Matlab жүйесi бұл жағдайда
сәттегi шексiз импульс шығысқа берiледi. Мұндай импульстi сипаттаманы тұрғызу мүмкiн емес. . Matlab жүйесi бұл жағдайда
 қабылдай отырып, қатаң дұрыс бөлiк үшiн импульстiк сипаттамсын тұрғызады. Бұл компьютер сапалы дұрыс емес нәтиже беретiн жағдайлардың бiрi.
қабылдай отырып, қатаң дұрыс бөлiк үшiн импульстiк сипаттамсын тұрғызады. Бұл компьютер сапалы дұрыс емес нәтиже беретiн жағдайлардың бiрi.
Егер жүйеде итеграторлар болмаса, импульстi сипаттама нөлге ұмтылады. Бұл шектi мән туралы теоремадан шығады:
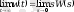 ,
,
мұндағы
 - жүйенiң берiлiстiк функциясы, ол
- жүйенiң берiлiстiк функциясы, ол
 үшiн Лаплас түрлендiруi болып табылады. Жүйенiң импульстi сипаттамасы бiр интегратормен тұрақты шамаға ұмтылады. Екi интеграторлы жүйе үшiн импульстiк сипаттама асимптотикалы түзуге, үш интеграторлы- параболаға ұмтылады.
үшiн Лаплас түрлендiруi болып табылады. Жүйенiң импульстi сипаттамасы бiр интегратормен тұрақты шамаға ұмтылады. Екi интеграторлы жүйе үшiн импульстiк сипаттама асимптотикалы түзуге, үш интеграторлы- параболаға ұмтылады.
1. 2.
Өтпелі процесті салмақ функциясы арқылы бағалау
Системаның кірісіне бірлік баспалдақты функция 1(t) түрінде сигнал берілді делік.
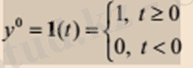 (1)
(1)
Сол кезде орныққан күй орнағанға дейін өтпелі процесс басталады. Мысалы электрогенератордағы жүктеме лезде (бір мезгілде, кенет) өзгергенде, қозғалтқыш (мотор) кірісіне лезде бірлік сыртқы əсер түсірілгенде, қадағалаушы сервомотордың кірісіндегі білік лезде айналған кезде т. б.
Өтпелі функция - системаның кірісіне 1(t) бірлік баспалдақты функция түсірілген кездегі системаның реакциясы:
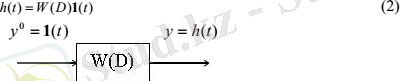
Егер y0 = N1(t) болса, онда системаның шығысында y = Nh(t) . Енді системаның кірісіне бірлік импульстік функция y 0 = d (t) күйіндегі сигнал берілсін
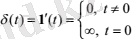 (3)
(3)
Бұл функция дельта-функция деп аталады.
2а суретте
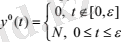 импульстік функция көрсетілген. Егер биіктікті (N) шексіздікке дейін өсіріп, бір мезгілде енін (e) азайтсақ жəне Ne=1 сақталатын болса, онда импульстің ауданы бірге тең болады. Осы функцияның ε → 0 кездегі шегі бірлік импульстік функция - дельта-функция болады.
импульстік функция көрсетілген. Егер биіктікті (N) шексіздікке дейін өсіріп, бір мезгілде енін (e) азайтсақ жəне Ne=1 сақталатын болса, онда импульстің ауданы бірге тең болады. Осы функцияның ε → 0 кездегі шегі бірлік импульстік функция - дельта-функция болады.
δ-функцияның негізгі қасиеті:
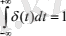 (бірлік аудан) .
(бірлік аудан) .
δ-функцияның тағы бір анықтамасы:
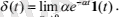
Салмақ функциясы y = w(t) (немесе системаның импульстік сипаты) - системаның кірісіне бірлік импульстік функция түсірілген кездегі системаның реакциясы
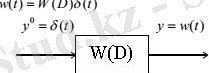 (4)
(4)
Егер системаның кірісіне бірлік емес импульстік функция келсе y 0 = Md (t) , онда шығысында да y(t) сондай есе (М есе) көп болады y = Mw(t) . Өтпелі функция мен салмақ функциясының байланысы. y 0 = N1(t) - N1(t - e ) , Ne = 1. Олай болса y(t) = W (D) y 0(t) болғандықтан y(t) = N[h(t) - h(t - e ) ] . Осы функцияның шегі салмақ функциясы болғандықтан
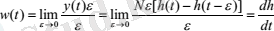 (5)
(5)
Демек, салмақ функциясы өтпелі функцияның уақыт бойынша туындысына тең. Өтпелі процесті салмақ функциясы арқылы бағалау. Беріліс функциясы салмақ функциясының бейнесі болып табылады (Лаплас түрлендіруі)
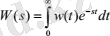 (6)
(6)
Динамикалық звеноның өтпелі функциясы мен оның беріліс функциясы арасындағы байланыс Карсон интегралдық түрлендіруі арқылы анықталады
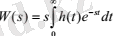 (7)
(7)
Бұған көз жеткізу үшін (6) бөлшектеп интегралдауды пайдаланамыз Жалпы жағдайда системаның кірісіне кез-келген y 0 = y 0(t) функция түріндегі сигнал келіп түсетін болса, онда бастапқы шарттар «нөл» болғанда өтпелі процесс Дюамель - Карсон интегралы арқылы анықталады
· өтпелі функция арқылы:
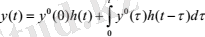
· салмақ функциясы арқылы:
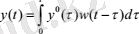
Типтік динамикалық звенолардың өтпелі сипаттарын қарастыруды 1-ретті апериодты динамикалық звенодан бастайық. Бұл звеноның дифференциалдық теңдеуі
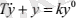
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz