Лаплас түрлендіруінің қасиеттері мен Меллин кері айналдыру формуласы


Қазақстан Республикасының Білім және ғылым министрлігі Шәкәрім атындағы Семей мемлекеттік университеті
Сызық автоматты түрлендіру жүйесі
СӨЖ
Тақырыбы: Лаплас түрлендіру қасиеттері
Орындаған: Қайсар Д. Б.
Тобы: АУ-401 С
Тексерген: Секербаева А. Б.
Семей 2015
Лаплас түрлендіруі
Жоспар:
- Түпнұсқа және бейне. Лаплас интегралы
- Бейненің қасиеті туралы
- Меллин формуласы
1. 1 Түпнұсқа және бейне. Лаплас интегралы.
Нақты айнымалы t-ның
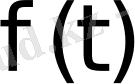 функциясы үшін мына шарттар орындалсын:
функциясы үшін мына шарттар орындалсын:
1) Айнымалы t-ның
 мәндерінде функция мәні
мәндерінде функция мәні
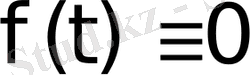 болсын;
болсын;
2) Нақты айнымалы t-ның
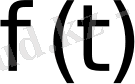 функциясы барлық
функциясы барлық
 мәндерінде үздіксіз болсын.
мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген
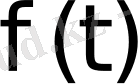 функциясының
функциясының
 өсу дәрежесі шектеулі болсын, яғни барлық
өсу дәрежесі шектеулі болсын, яғни барлық
 мәндерінде
мәндерінде
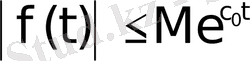 теңсіздігі орындалатындай
теңсіздігі орындалатындай
 және
және
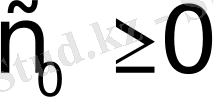 сандары табылсын. Осы шартты қанағаттандыратын
сандары табылсын. Осы шартты қанағаттандыратын
 сандарының ең кішісі
сандарының ең кішісі
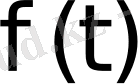 функциясының өсу көрсеткіші деп аталады.
функциясының өсу көрсеткіші деп аталады.
Осы (1) -(3) шарттарды қанағаттандыратын
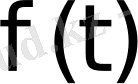 функциясы түпнұсқа деп аталады.
функциясы түпнұсқа деп аталады.
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын
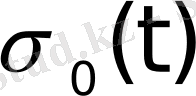 функциясы,
функциясы,
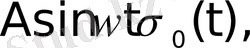
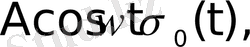
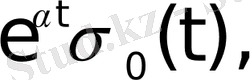

 функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы
 уақыт кезеңі ретінде алуға болады. Сонда t
уақыт кезеңі ретінде алуға болады. Сонда t
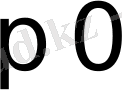 болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген f(t) функциялары үшін орындалады.
Егер осы (1) -(3) шарттардың ең болмағанда біреуі орындалмаса, онда f(t) функциясы түпнұсқа болмайды. Мысалы,
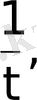
 функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші
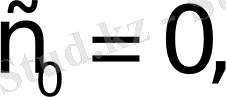 өйткені
өйткені
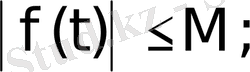
б) Барлық
 түріндегі дәрежелік функциялар. Бұлар үшін
түріндегі дәрежелік функциялар. Бұлар үшін
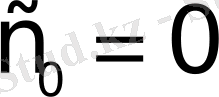 болады. Шынында да
болады. Шынында да
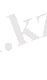
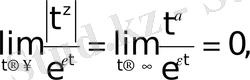
өйткені
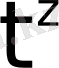 -тің модулі
-тің модулі
 көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
 -қаншалықты болса да аз оң сан.
-қаншалықты болса да аз оң сан.
Осыдан
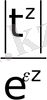 функциясының
функциясының
 аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
 мәндері үшін
мәндері үшін
 , немесе
, немесе
 теңсіздігі орындалады.
теңсіздігі орындалады.
Мұндағы А-кез-келген оң сан,
 -қаншалықты болса да аз оң сан. Сондықтан
-қаншалықты болса да аз оң сан. Сондықтан
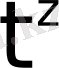 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
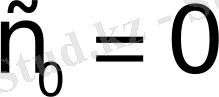 болады.
болады.
Егер
 болса, онда
болса, онда
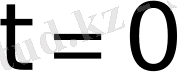 үзіліс нүктесі болады да
үзіліс нүктесі болады да
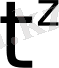 функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Жоғарыдағы
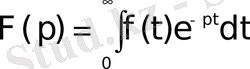 (1)
(1)
теңдігімен анықталған
 комплекс айнымалының
комплекс айнымалының
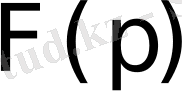 функциясы
функциясы
 функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
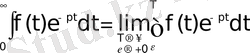 (2)
(2)
Мұндағы
 оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
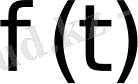 функциясы мен оның
функциясы мен оның
 бейнесі арасында сәйкестік орнатылады.
бейнесі арасында сәйкестік орнатылады.
Берілген
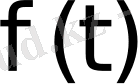 функциясы бойынша оның
функциясы бойынша оның
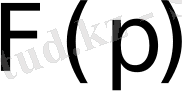 бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
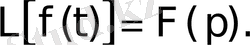
Егер
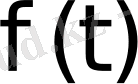 функцияға
функцияға
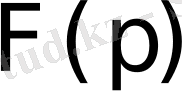 бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
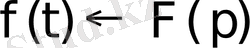 немесе
немесе
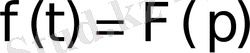 .
.
Егер (2) теңдіктің оң жағындағы шек бар болатын болса, онда Лаплас интегралы жинақталады.
Енді Лаплас бойынша қандай
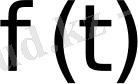 функцияларын түрлендіруге болатынын қарастырайық.
функцияларын түрлендіруге болатынын қарастырайық.
Теорема 1. 1
Егер
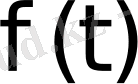 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады және оның
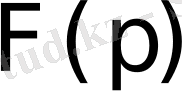 бейнесі
бейнесі
 жарты жазықтығында анықталған.
жарты жазықтығында анықталған.
Мұндағы
 деп
деп
 функциясының өсу көрсеткішін ұғамыз.
функциясының өсу көрсеткішін ұғамыз.
Теореманы дәлелдеу үшін р комплекс айнымалысының жазықтығының
 теңсіздігі орындалатын бөлігінде (1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
теңсіздігі орындалатын бөлігінде (1) теңдіктің оң жағындағы интеграл жинақталатындығын көрсетсек жеткілікті.
Түпнұсқаның (3) шартын пайдаланып мынадай теңсіздіктер аламыз:
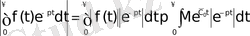
Ал
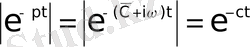 болғандықтан
болғандықтан
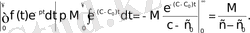 (3)
(3)
Мұндағы
 болғандықтан,
болғандықтан,
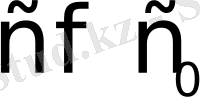
 болса, Лаплас интегралы жинақталады. Сонымен,
болса, Лаплас интегралы жинақталады. Сонымен,
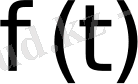 функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
функциясы түпнұсқа болса, онда оны Лаплас бойынша түрлендіруге болады. Оның
 бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
бейнесі р комплекс айнымалысы жазықтығының жорымал оске параллель және одан
 қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.
қашықтықта өтетін түзуден оңға қарай бөлігінде анықталған.

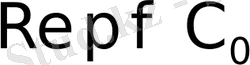
0
 С
С
1. 1 Сурет
Осы теоремадан
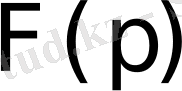 бейнесінің мынадай қасиетін алуға болады.
бейнесінің мынадай қасиетін алуға болады.
Егер (3) теңсіздікте
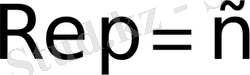 шексіздікке ұмтылса, онда Лаплас интегралының модулі нолге ұмтылады.
шексіздікке ұмтылса, онда Лаплас интегралының модулі нолге ұмтылады.
Осыдан
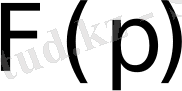 функциясы бейне болса, онда
функциясы бейне болса, онда
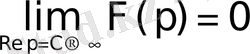 (4)
(4)
болатындығы шығады.
Теорема 1. 2 Бейненің қасиеті туралы
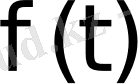 түпнұсқаның
түпнұсқаның
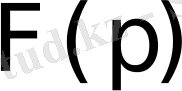 бейнесі
бейнесі
 шарты орындалатын жарты жазықтықта аналитикалық функция болады.
шарты орындалатын жарты жазықтықта аналитикалық функция болады.
Мұндағы
 -түпнұсқаның өсу көрсеткіші.
-түпнұсқаның өсу көрсеткіші.
Анықтама
Мына
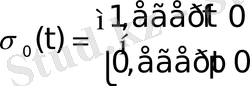 болса,
болса,
шартымен анықталған
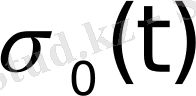 функциясы Хевисайдтың бірлік функциясы деп аталады.
функциясы Хевисайдтың бірлік функциясы деп аталады.
Осы
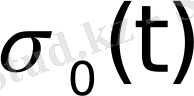 функциясы түпнұсқа болады. Оның өсу көрсеткіші
функциясы түпнұсқа болады. Оның өсу көрсеткіші
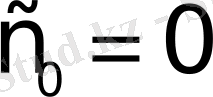 . Бұл функцияның мәні
. Бұл функцияның мәні
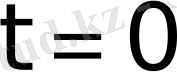 болғанда анықталмаған, өйткені Лаплас интегралын есептегенде
болғанда анықталмаған, өйткені Лаплас интегралын есептегенде
 функциясының
функциясының
 болғанда қандай мән қабылдайтыны ескерілмейді.
болғанда қандай мән қабылдайтыны ескерілмейді.
Дегенмен де,
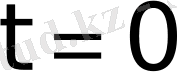 нүктесіндегі мәні үшін әдетте
нүктесіндегі мәні үшін әдетте


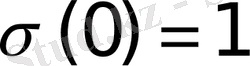 мәндерін алады.
мәндерін алады.
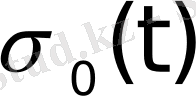
1
t
0
1. 2 Сурет
Берілген
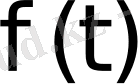 функциясы -
функциясы -
 аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал
аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал
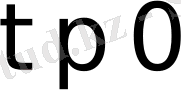 болғанда
болғанда
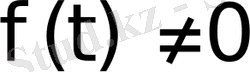 шарты орындалсын. Егер
шарты орындалсын. Егер
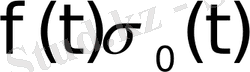 функциясын қарастырсақ, яғни
функциясын қарастырсақ, яғни
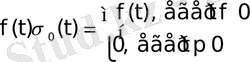 болса, (6)
болса, (6)
онда
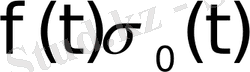 функциясы түпнұсқа болады. Мұндағы
функциясы түпнұсқа болады. Мұндағы
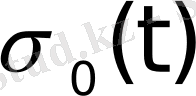 көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта
көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта
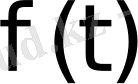 функциясының Лаплас түрлендіруінде
функциясының Лаплас түрлендіруінде
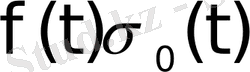 функциясы берілген деп есептеп, оның орнына қысқаша
функциясы берілген деп есептеп, оның орнына қысқаша
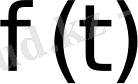 деп жазамыз.
деп жазамыз.
Енді кейбір функциялардың бейнесін анықтама бойынша табу мысалдарын келтірейік.
1. 3 Меллин формуласы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz