Компьютерлік схемотехниканың арифметикалық негіздері. ЭЕМ құрудың классикалық негіздері жайлы
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:
Қазақстан Республикасының Білім және Ғылым министрлігі
Семей қаласының Шәкәрім атындағы Мемлекеттік университеті
СӨЖ
Тақырыбы: Компьютерлік схемотехниканың арифметикалық негіздері. ЭЕМ құрудың классикалық негіздері
Орындаған: Талғатова Ш. Т
Тобы: Иф - 203, 4 курс
Тексерген : Тлеубаева А. Б
Семей қаласы
2015 жыл
Жоспар:
І. КІРІСПЕ
ІІ. НЕГІЗГІ БӨЛІМ
2. 1 Компьютерлік схемотехниканың арифметикалық негіздері
2. 2 ЭЕМ-де сандарды көрсету әдістері
2. 3 Компьютерлік схемотехниканың логикалық негіздері
2. 4 ЭЕМ-ді құрудың классикалық негіздері
ІІІ. ҚОРЫТЫНДЫ
ІV. ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ
Кіріспе
Қазіргі кезде сұлбатехниканың мәні орасан зор. Қазіргі микросұлбатехниканың негізгі принциптерінің өзектілігі аспаптарға жаппай интегралдық сұлбалардың енгізілуіне негізделген. ИС және электрониканың басқа да құрылғыларын инженерлер, техниктер және жұмысшыларда қолданады. ИС дұрыс қолдану үшін әртүрлі электронды құрылғылардың құрылымдарын қамтитын күрделі және кеңейтілген құжаттарды қолдану қажет. Сұлбатехника қазіргі ИС да және микроэлектронды аппараттарда қолданылатын сұлбатехникалық шешімдердің шығуын түсіндіреді және жобалаушыға өз бетімен жаңа ИС типтерін өңдеуге және оның негізінде құрылғылар жасауға мүмкіндік береді.
Сұлбатехника - жас маманның кәсіби әрекетіне өте қажет практикалық дағдыларын қалыптастыруға арналған. Кез келген ақпарат өңдеуші жүйенің негізгі параметрлерін анықтау есебімен кездеседі. Функциональды жобалау кезеніңдегі сауатты жүргізілген жобалау және құрастыру кезеңдерінде орасан күштер мен құралдарды үнемдеуге мүмкіндік береді. Сондықтан «Сұлбатехника» пәні «Ақпараттық жүйелер» мамандығының базалық пәндеріне жатады.
- Компьютерлік схемотехниканың арифметикалық негіздері
Компьютердегі сандық ақпарат төмендегідей сипатталады:
- санау жүйесімен (екілік, ондық) ;
- сан түрімен (нақты, космплексті, массив) ;
- сан типімен (аралас, бөлшек, бүтін) ;
- сандарды көрсету аралығымен және дәлдігімен;
- терім сандарды кодтау әдістерімен;
- арифметикалық операцияларды орындау алгоритмдерімен.
Санау жүйесіне анықтама берейік: санау жүйесі - цифрлік белгілер (алфавит) жиыны көмегімен сандарды жазу әдістері мен ережелерінің жиыны. Цифрлік белгілердің санын санау жүйесінің негізі деп атайды.
Санау жүйесінің екі типі болады:
- позициялық, әрбір цифрдің мәні санды жазғандағы оның орнымен анықталады;
- позициялық емес, әрбір цифрдің мәні санды жазғандағы оның орнына тәуелді емес.
Позициялық емес санау жүйесінің мысалы римдік санау жүйесі болады: IX, IV, XV және с. с.
Позициялық санау жүйесіне күнделікті қолданылатын ондық санау жүйесін айтуға болады.
Позициялық жүйеде кез келген бүтін санды көпмүшелік түрінде жазуға болады:
X s ={A n A n-1 . . . A 1 A 0 } s =A n S n +A n-1 S n-1 + . . . +A 1 S 1 +A 0 S 0
мұндағы s - санау жүйесінің негізі;
А- осы санау жүйесінде жазылған санның мәндік
цифрлары;
n - санның разрядтар саны.
Мысал 1. 5341 10 санын көпмүшелік түрінде жазайық:
5341 10 =510 3 +310 2 +410 1 +110 0
Мысал 2. 321 10 санын екілік санау жүйесінде жазайық. Ол үшін санды 2-дәрежелі сандардың қосындысы түрінде жіктеп жазу керек.
321 10 =12 8 +12 6 +12 0
Одан соң екі дәреже болған кездегі коэффициенттерін оңнан солға қарай жазамыз (минималды нөлінші дәрежеден максимал дәрежеге қарай)
Сондықтан бұл сан екілік санау жүйесінде 1011 2 түріне келеді.
Екілік санау жүйесіндегі сандармен орындалатын арифметикалық операциялар :
1. Қосу операциясы бір разрядта екілік қосу кестесі көмегімен орындалады:
+ 0 1
0 0 1
1 1 10
Мысал 3.
1001 2 1101 2 2
1010 2 1011 2 1 2
10011 2 11000 2 1 2
2. Алу операциясы алу кестесі көмегімен орындалады, ондағы 1 үлкен разрядтан алынады.
- 0 1
0 0 11
1 1 0
Мысал 4.
101110011 2 110101101 2
100011011 2 1010 2
001011000 2 001001110 2
3. Көбейту операциясы кәдімгі ондық санау жүйесіндегі сызба бойынша орындалады.
х 0 1
0 0 0
1 0 1
Мысал 5.
х 11001 2 х 101 2
1101 2 11 2
11001 101
11001 101
11001 2
101000101 2
4. Бөлу операциясы 10-ық санау жүйесінде пайдаланылатын алгоритмге ұқсас алгоритм бойынша жүргізіледі.
Мысал 6.
101000101 2 1101 2 100011000 2 2
1101 1101 2 10010 2
1110 0010100
1101
1101 1010 2 -остаток
1101
0
2. 2 ЭЕМ-де сандарды көрсету әдістері
Біз білетіндей сандарды көрсетудің екі негізгі әдістері бар: бекітілген және жүзуші үтірі бар . Көптеген әмбебап ЭЕМ-дер жүзуші үтірі бар сандармен жұмыс істейді, ал көптеген арнайы ЭЕМ-дер бекітілген үтірі бар сандармен жұмыс істейді.
Бірақ машиналардың бірқатары екі форматтағы сандармен жұмыс істей береді.
Жалпы жағдайда сандарды көрсету әдісі бағдарламалау сипатына үлкен әсер етеді. Бекітілген үтірі бар жүйеде жұмыс істейтін ЭЕМ-де бағдарламалау қиын өйткені арифметикалық қиындықтан басқа үтірдің тұрған орнын анықтау керек.
Бекітілген нүкте. Машинаның разрядтық торында разрядтың тұрақты саны болады деп келісейік - n.Ьекітілген нүктесі бар сандарды көрсеткен кезде үтір әрқашан да үлкен разрядтың алдында тұр деп есептеледі, ал есептеуге қатысатын барлық сандар абсолют өлшемі бойынша бірден кіші деп есептеледі:
X < 1
Сандардың сипаттамаларын енгізейік:
өзгеру аралығы
және
көрсету дәлдігі
.
Өзгеру аралығы машина әрекет ететін сандардың орналаса алатын шектерімен сипатталады.
0-ге тең емес ең кіші сан:
Осылайша ЭЕМ жұмыс істейтін сандар аралығы :
X
min
X
X
max
2
-n
X
1 - 2
-n
2. 3 Компьютерлік схемотехниканың логикалық негіздері
Кәдімгі алгебрадан басқа арнайы алгебра бар. Оның негізін ХІХ ғ. математигі Дж. Буль салған. Бұл алгебра пікірлерді есептеумен айналысады.
Оның ерекшелігі дискреттік құрылғылардың жұмысын сипаттауға қолдану болып келеді. Ондай құрылғылар қатарына есептеу техникасы және автоматика құрылғыларының бір классы жатады.
Мұнда алгебраның өзі құрылғының үлгісі рөлін атқарады. Ол көрсетілген типтегі еркін құрылғының жұмысы осы алгебраның көмегімен қандай да бір жағынан тек қана сипатталуы мүмкін дегенді білдіреді. Шындығында нақты құрылғы физикалық логика алгебрасында сипатталғанна бөлек жұмыс істейді.
Логика алгебрасының функцияларына қатысты бірнеше синонимдер бар:
- логикаалгебрасының функциялары;
- ауыстырып қосқышфункциялары;
- бульдікфункциялар;
- екілікфункциялар.
Қажеттілігінше бұл синонимдердің барлығын пайдаланамыз.
Аргументтердің қандай да бір жиынын қарастырайық:
<X 1 , X 2 , X 3 , . . . Х i , . . . X n >
және де аргументтердің әрқайсысы басқаларынан тәуелсіз екі мүмкін мәннің біреуін қабылдайды деп келісеміз.
X i = {0, 1}
Бір және екі айнымалыға тәуелді бірнеше бульдік функцияларды қарастырайық.
Ол үшін аргументтердің барлық терімдеріне оның мәндерін беру керек.
Екі аргументке тәуелді барлық ЛАФ-ын қарастырайық та оларды бір кестеге жазайық:
Функция
№
f(X 1 , X 2 ) =0
f(X 1 , X 2 ) = X 1 & X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 · X 2
f(X 1 , X 2 ) = X 1 X 2
X 1 Δ X 2
f(X 1 , X 2 ) = X1
X 2 Δ X 1
f(X 1 , X 2 ) = X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 + X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1
X 2
f(X 1 , X 2 ) = X 1 ~X 2
f(X 1 , X 2 ) =^X 2
f(X 1 , X 2 ) =X 2
f(X 1 , X 2 ) = X 2
X 1
f(X 1 , X 2 ) =^X 1
f(X 1 , X 2 ) = X 1
f(X 1 , X 2 ) = X 1
f(X 1 , X 2 ) = X 1 X 2
f(X 1 , X 2 ) =1
Логикалық элементтер, ЭЕМ-де логикалық функцияларды іске асыру. Логикалық элементтердің функционалды -толық жүйелері
Қандай да бір күрделі пікірге қандай мағыналық мазмұн енгізуге болатынын 2 аргументті ЛАФ-ы мысалында қарастырайық.
Инверсия. Х ЕМЕС немесе 'Х' -ті теріске шығару деп оқылады.Мысалға мынадай пікірді алайық: А=<Киев-Франция астанасы>, онда күрделі А ЕМЕС пікірі А дұрыс емес екенін, яғни <Киев-Франция астанасы> емес екенін білдіреді.
Қарапайым пікірлерден күрделі пікірлерді байланыстарды қолданып құруға болады.
Логикалық байланыстар- аргументтері қарапайым пікірлер болып келетін ЛАФ-ры.
Конъюнкция. Екі пікірді алайық:А=<Москва - РФ астанасы>
В=<екі-екім төрт>
онда А & В күрделі пікірі ақиқат болады, өйткені бұл екі пікір де ақиқат.
Егер ақиқат пікірге '1' мәнін ал жалғанға '0' мәнін жазсақ онда пікірді көбейтінді деп айтуға болады. Бұл жағдайда конъюнкция үшін ақиқаттық кестесі көбейту кестесіне сәйкес келеді.
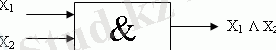0
Конъюнкция функциясы екі пікір бір уақытта ақиқат болған жағдайда ғана ақиқат.
Дизъюнкция. Бір күрделі пікір оған кіретін пікірлердің кем дегенде біреуі ақиқат болған жағдайда ақиқат болады.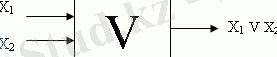
f
1
(X
1
, X
2
)
X 1 НЕМЕСЕ X 2 деп оқылады:
Еркін құрылғыны синтездеу техникалық (физикалық) есебі ЛАФ-ын құру математикалық есебіне әкелінеді.
Еркін ЛАФ-ын құру үшін байланыстың қандай көлемі қажет деген сұрақ әрине пайда болады. Бұл сұрақтың жауабы бірмәнді емес. Мысалы f 0 (0 тұрақтысы), f 15 (1 тұрақтысы) функциялары көмегімен еркін ЛАФ-ын құруға болмайтынын көреміз. Оны тек инвертордың көмегімен құру да мүмкін емес. Бірақ оны f 7 , f 1 , f 10 немесе f 7 , f 1 , f 12 көмегімен құруға болатыны анық.
Бұл элементар ЛАФ-ның жиыны
конъюнкция, дизъюнкция
және
теріске шығарудың
базисі
деп аталады. ЛАФ-ын математикалық ұйымдастыру кезіндегі ең кең тараған базис. Бұдан басқа базистер де бар:
, +, 1,
Сол сияқты бір элементті базистер бар: f 8 - Пирса тілсызығы, f 14 - Шеффер штрихы, ЖӘНЕ-ЕМЕС, НЕМЕСЕ-ЕМЕС.
Құрылғының техникалық синтезі үшін нақты құрылғыны құруға мүмкіндік беретін, ЛАФ-ры базис құратын элементтердің қандай да бір терімі болуы керек.
Бірақ, айтып кеткендей ЛАФ-ын синтездеу есебі - идеал модель.
Логика алгебрасы функцияларын минимизациялау және оны қарастырғандағы шектеулер.
Мүлтіксіз дизъюнктивті қалыпты форма (МДҚФ) жазудың тиімді формасы болмайтынын мысалда көрсетейік:
f(Х
1
, Х
2
) = Х
1
Х
2
Х
1
Х
2
Х
1
Х
2
=Х
1
Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Сонымен құрылғыны синтездеу есебі ондағы жабдықтарды азайту есебімен толықтырылуы керек. Математикалық көзқарастан бұл есеп минималды ЛАФ-ын құру есебі.
Минималды ЛАФ-ы дегеніміз бастапқы формадағыдан аз әріптер санына тұратын форма.
Егер қандай да бір терімде f а
1
мінін қабылдаса, ал
а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
функциясының а
2
мәнін жабады деп айтады.
ЛАФ-ын минимизацилаған кезде бастапқыға қарағанда аз әрпі бар форманы алуға тырысады.
Дизъюнктивті қалыпты формаға қатысты бұл форманы қысқартылған дизъюнктивті қалыпты форма (Қысқ. ДҚФ) деп атайды. ҚДҚФ құрудың мәні оның құрамына бастапқы функцияның бір емес бірнеше бірлігін жабатын бірліктері бар элементар көбейтулер кіреді.
ҚДҚФ - ға кіретін әрбір элементар көбейтінді функцияның тек бір бірлігін жабады.
ҚДҚФ-ны алу тәртібі төмендегідейболуы мүмкін.
1. Бастапқы МДҚФ-ның бірліктерінің конституенттеріне барлық толық емес жабыстыру операцияларын орындау. (n-1) -рангті көбейтінділер шығады. Қалған жапсырылмаған бірліктің конституенттері келешектегі жабыстыруларға қатыса алмайды.
2. Алынған барлық бірлік конституенттерімен көбейтінділерінің жабуын жүргізу. Кейбір бірлік конституенттерінің бөлігі шектеледі.
3. 1) және 2) операцияларын мүмкін болғанша жүргізу.
Мысал 1.
f(Х 1 , Х 2 ) = Х 1 Х 2
Егер толық жабыстыру операциясын қолдансақ онда:
f(Х 1 , Х 2 ) = Х 1
немесе
f(Х 1 , Х 2 ) = Х 1 Х 2
яғни, операцияны ары қарай жүргізуге мүмкіндік жоқ.
Енді толық емес жапсыру операциясын қолданайық:
f(Х 1 , Х 2 ) = Х 1
Х 1 , Х 2 - қарапайым импликанттар
Х 1 Х 2 , Х 1 Х 2 , Х 1 Х 2 - бірліктің коституенттері
Енді жою операциясын жүргізе аламыз:
Х 1 Х 1 -ді жояды, Х 1 Х 2 , Х 1 Х 2
Х 2 Х 2 - ні жояды, Х 1 Х 2 , Х 1 Х 2
Яғни Қысқ. ДҚФ
f(Х
1
, Х
2
) = Х
1
Х
2
біздің жағдайымызда бұл минималды форма
Толығымен анықталған функцияларды минимизациялау.
Нақты құрылғының жұмысы көп жағдайда толығымен анықталмаған функция көмегімен сипатталады, өйткені кіру сигналдарының кейбір комдинациялары берілмейді немесе рұқсат етілмеген болып келеді.
Анықтама: Толық анықталмаған функция аргументтердің кейбір терімдерінде мәндері еркін болатын ауыстырып қосқыш функция болады (яғни, “0” немесе “1”-ге тең) .
Анықтама:
f(x
1
, x
2
, . . . x
n
) функциясы аргументтердің “p” терімінде анықталмаған болсын. Онда толық анықталған
(x
1
, x
2
, . . . x
n
) функциясын f(x
1
, x
2
, . . . x
n
) функциясына эквивалентті деп санаймыз, егер оның мәндері f(x
1
, x
2
, . . . x
n
) анықталған терімдердегі мәндермен сәйкес келсе.
f(x 1 , x 2 , . . . x n ) - ға эквивалентті әр түрлі 2 р функциялары бар екені анық.
f(x
1
, x
2
, . . . x
n
) - ді минимизациялау есебі дегеніміз формасы қарапайым эквивалентті
(x
1
, x
2
, . . . x
n
) - ді таңдау.
Толығымен анықталмаған функцияларды Вейч диаграммаларының көмегімен минимизациялау көрнекті және ыңғайлы түрде минималды формаларды іздеп табуға көмектеседі.
Мысал: f(x 1 x 2 x 3 x 4 ) функциясын қарастырайық та оның минималды формасын табайық. Вейч диаграммасын келесі ережелерге сәйкес толтырайық: бірліктің конституенттеріне сәйкес келетін ұяшықтарға бірлерді қоямыз, жоқ конституенттер үшін - нөлдерді, қалған ұяшықтарға «*» (жұлдызша) - анықталмағандық символын қоямыз.
... жалғасыСіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz