Кешігу буындары

Пән: Автоматтандыру, Техника
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министірлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

«Автоматика және элекротехника» кафедрасы

СӨЖ

Тақырыбы: Кешігу буындары.

Орындаған: Сиязбек Д. С.

Тобы: АУ-301

Тексерген: аға оқытушы Секербаева А. Б.

Семей 2015 ж.

Мазмұны:

1. Негізгі бөлім . . . 2

1. 1. Кешігу буын(жиілік сипаттамасы) . . . . . . . . . 3

1. 2. Жүйенің математикалық нобайын анықтау . . . 4

Қорытынды. . 5

Әдебиеттер. . . ……5

Негізгі бөлім

Қазіргі таңда автоматты басқару теориясында кешігуі бар жүйелерге үлкен көңіл бөлінуде. Бұл кешігуі бар жүйелерді басқарудың есептері ғылым мен техниканың әр түрлі салаларында туындайтындығымен түсіндір -іледі.

Кешігу буыны теңдеуі y(t) =x(t) (t-τ) ; мұнда τ - таза кешігу уақыты . Кешігу буыны кірістік сигналдарды форма жағынан өзгертпей, бірақта τ уақытына кешіктіріп шығарады. Буынның беріліс функциясы W(s) = е - S

Өтпелі функциясы

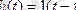
Яғни, өтпелі сипаттамасы τ. уақытына кешіккен бірлік сатылы ықпалды қайталайды.

Импульстік өтпелі функциясы ω(t) =δ(t-τ) .

Жиіліктік сипаттамалары

Буынның КБФ-сы .

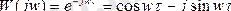Буынның АФЖС центрі кординатаның бас нүктесінде орналасқан бірлік радиусты шеңбермен сипатталады

КБФ-ың модульі

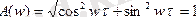
КБФ-ың аргументі φ(ω) =-ω*τ, яғни, жиіліктің және кешігу уақытының өсуімен, шығыстық тербелістің фаза жағынан қалыс қалуы ұлғая түседі.

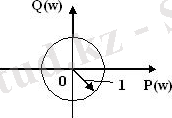
Сурет 1. Буынның АФЖС

ЛАЖС-ың өрнегі L(ω) =0, яғни күщейту эффектісі жоқ, сипаттама нақты өспен беттеседі (2. а сурет)

Буынның ЛФЖС-ың абсолюттік мәні жиіліктің және кешігу уақытының өсуімен ұлғаяды (2. б сурет) .

а) 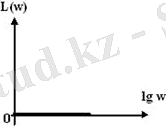б)

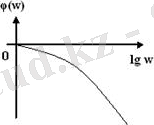
Сурет 2. Буынның а) - ЛАЖС және б) - ЛФЖС

1. 1. Кешігу буын(жиілік сипаттамасы)

Буынның жиiлiктiк берiлiс функциясы 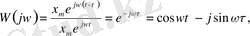мұндағы 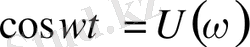және 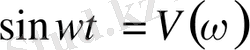сәйкесiнше нақты және жорамал жиiлiктiк сипаттамасы болып табылады. Берiлiс функциясы . . 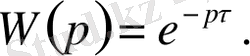Жиiлiктiк берiлiс функциясының модулi 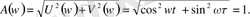. Жиiлiктiк берiлiс функциясының аргументi 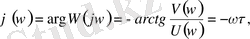АФС центрi координат басында болатын бiрлiк радиусты шеңбер түрiнде болады, өйткенi модуль бiрге тең, ал фаза пропорционалдык коэффициентi бар жиiлiкке пропорционал. 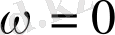кезiнде

векторы оң нақты ось бойында орналасады. Жиiлiк өскенде, вектор ұзындығын өзгертпестен, сағат тiлiнiң бағыты бойымен айналады, ал жиiлiк 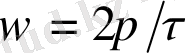мәнге жеткенде, вектор 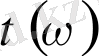бұрышын арттыра отырып, толық бiр айналым жасайды. Осымен кешiгу буыны фазалық ығысуы шектi мәнге (оң не терiс) ие буындардан елеулi түрде өзгешеленедi. Логарифмдiк амплитудалық сипаттама жиiлiк осiмен үйлеседi 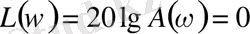ал логарифмдiк фазалық сипаттама (6. 73) формула бойынша жартылай логарифмдiк масштабта салынады.

Кешігу буынының ерекшелігін былайша атап өтуге болады: кешігу буыны кірістік сигналды ешқандай өзгеріссіз буынның шығысына 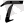уақыт өткеннен кейін шығарады 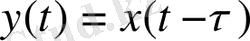; Бұл буынның беріліс функциясы 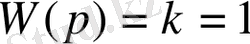; Бұл буын амплитудалық жиіліктік сипаттамасы бойынша инерциясыз буынға парапар, яғни ол амплитудалық қатынастары ұқсас жоғарыжиіліктік және төменгі жиіліктік сигналдардың бәрін бірдей өткізеді. Ал, фазалық жиіліктік сипаттамасы бойынша жиілік 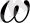және кешігу уақыты 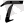параметрлеріне пропорционал теріс таңбалы фазалық ығысу туғызатындықтан ол апериодтық буынға парапар.

1. 2. Жүйенің математикалық нобайын анықтау
Параметрлері таралған жүйелердің мысалы ретінде электр энергиясын қашықтыққа тасымалдауға арналған ұзын желілер қарастырылады.

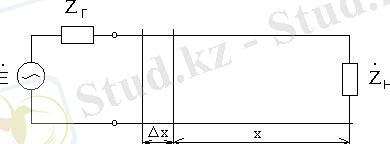
Сурет 1. Электр энергиясын қашықтыққа тасымалдаушы ұзын желінің эквивалентті схемасы.

Шығынсыз желілер келесідей дербес туындысы бар дифференциалдық теңдеулермен сипатталады:

,
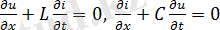Олардың шешімі:

.
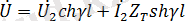
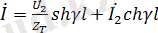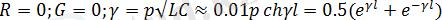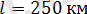; желі ұзындығы ; ескере отыра мынадай шешімге келеміз:
,
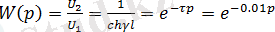мұндағы 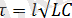. Мұндағы τ таза кешігу уақытын сипаттайтын шама, l -желі ұзындығы, LC тізбек параметрлері. Қорытындысында біз таза кешігу буынын аламыз, яғни шығынсыз желілер таза кешігу буыны болады деген қорытынды жасаймыз, бірақ олар ұзын желіні толық сипаттайды деп айта алмаймы себебі біз тек желінің соңы мен басындағы кернеудің тәуелділігін ғана алдық.
Электр энергиясын тасымалдаушы бірфазалы ұзын желілер келесідей дербес туындылары бар дифференциалдық теңдеулермен сипатталады:
-
-
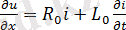
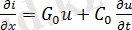
Осы теңдеулердің шешімі жоғарыда айтылғандай гиперболалық функциялар түрінде болады. Нәтижесіде беру функциясы келесі түрде болады (желінің соңындағы кернеу мәнінің желі басындағы кернеу мәніне қатынасы) :

мұндағы
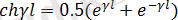
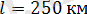желі ұзындығы ;
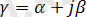- таралу тұрақтысы
;
;
;
;
;

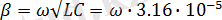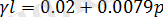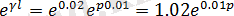Беру функция күрделі кешігу буыны болатынын көреміз:

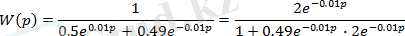
Қорытынды: Кешігу буыны кірістік сигналды ешқандай өзгеріссіз буынның шығысына 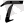уақыт өткеннен кейін шығарады 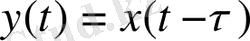; Бұл буынның беріліс функциясы 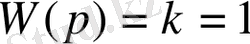; Бұл буын амплитудалық жиіліктік сипаттамасы бойынша инерциясыз буынға парапар ал, фазалық жиіліктік сипаттамасы бойынша жиілік 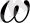және кешігу уақыты 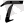параметрлеріне пропорционал теріс таңбалы фазалық ығысу туғызатындықтан ол апериодтық буынға парапар.