Ляпунов тұрақтылығы және Ляпунов теоремалары: теориясы мен қолданбалары

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министірлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

«Автоматика және элекротехника» кафедрасы»

СӨЖ

Тақырыбы: Ляпунов тұрақтылығы

Орындаған: Болатова А. А

Тобы: АУ-301

Тексерген: аға оқытушы Секербаева А. Б.

Семей 2015 ж.

Жоспар:

1Ляпунов бойынша орнықтылық есебінің жалпы қойылымы.

2Ляпуновтың ассимптотикалық тұрақтылық теоремасы.

3Ляпунов теоремасы.

4Ляпуновтың Quot

5Пайдаланылған Әдебиеттер

Ляпунов бойынша орнықтылық есебінің жалпы қойылымы.

АБЖ пайдалану тәртібі кезінде, қалыпты объектілерге әсер ететін қозған әсерге тәуелсіз объектілердің анықталған жұмыс режимдерін қолдау керек. Жүйенің орнықтылығы бұл кіріс дабылдарының немесе кез келген әсерлердің аз өзгерісі. Жүйенің орнықтылығы бұл АБЖ параметрлері немесе басты шарттарында кіріс дабылының аз өзгерісі шығыс дабылының ауытқуына әкелмеуін білдіреді.

АБЖ барлық үрдістер дифференциалдық теңдеулермен жазылатындықтан, орнықтылықтың математикалық анализі осы теңдеулерді шешу қасиеттерін зерттеуге біріктіріледі. Теңдеулердің шешуін х _1, х _2, х _n айнымалылар кеңістігінде х(t) траекториясы ретінде қарастыруға болады.

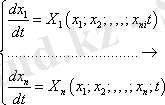векторлық формада

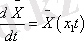
Көп траекториялардың ішінен бір g(t) алайық және оның орнықтылығын зерттейік, яғни g(t) траекториясының маңайында бастапқы t ₀ моментте басталатын х(t) траекториясының қасиетін зерттейік. Егер олар әр уақытта g(t) траекториясының маңайында болса, онда жүйе орнықты, егер g(t) маңайынан ауытқыса, онда бұл жүйенің орнықсыздығын сипаттайды.

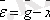жаңа айнымалыны еңгізейік

Онда 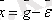және

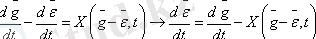
немесе

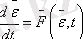
g(t) траекториясына 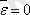нүктесі сәйкес келеді. 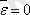нүктесі тепе-теңдік күйі болып табылады, яғни

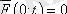
егер g(t) =0 және жүйенің операторы стационар болса, онда мұндай жүйе автономды деп аталады. Мұндай жағдайларда ,

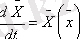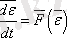
Орнықтылықтың математикалық анықтамасы

Тұрақтылық математикалық ұғым 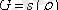кейбір аймақтары сфера деп есептейік. Осы сфералы аймақтың болуына Коши шарты орындалады және жүйенің бірлік шешімі

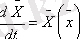
Онда осы аймақтың әрбір нүктесінде кейбір х(t) траекториясы өтеді. Жүйенің тепе-тендік күйі бастапқы коорднаторлармен теңестірілген.

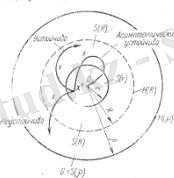
1 сурет

Тепе-тендік күйі орнықтытиісті болып саналады теңдік жағдайыдепесептейміз, егер кез-келген R<ρ үшін r ≤ R болатын болса, яғни S(r) сфералық аймағында х ₀ нүктесінен басталса, х(t) траекториясы әр қашанда S(R) сфералық аймақта қалса тепе-теңдік күйі орнықты болып есептелінеді.

Егер R<ρ, онда S(R) сфералық аймақта басталатын х (t) траекториясы уақыттың шексіз артуы кезінде бастапқы координатаға ұмтылса асимптотикалық күйорнықтыдеп есептелінеді.

Егер R<ρ немесе R<r, онда S(r) сфералық аймақтағы X ₀ нүктесінен басталатын х(t) траекториясы H(R) сферасына шекті уақытта жетсе күй орнықсыз деп есептеледі.

Ляпуновтың ассимптотикалық тұрақтылық теоремасы.

Автономды сызықтық жүйенің нолдік шешімі асимтотикалық тұрақты болу үшін оң анықталған Q матрица үшін анықталған Р матрица болу керек және ол келесі теңдеуді қанағаттандыру керек.

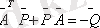
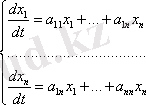
Сызықтық жүйе теңдеулер жүйесінде жазылады немесе

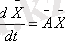
мұндағы

матрица теңдеуін сипаттайтын түбір анализімен байланысты келтірілген қатарға басқа әдіс қолданылады:

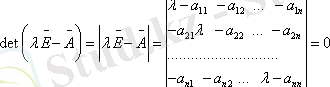
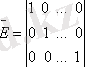- бірлік матрица

Анықтауышты ашып жазсақ

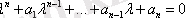
Егер теңдеудің барлық түбірлерінің теріс заттық бөлігі болса, онда жүйенің нолдік шешімі асимптотикалық орнықты.

Егер теңдеудің түбірлерінің арасында нолдік заттық бөлігі бар түбірі болса, онда орнықты да орнықсыз да бола алады. біреуі заттық оң бөлігі болса, онда жүйенің нолдік шешімі орнықсыз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.