Регрессиялық талдаудың мақсаты мен есептері

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

ОӨЖ

Регрессиялық талдаудың мақсаты мен есептері

Орындаған: Қадырова Ж. Р.

Тобы: УА-303

Тексерген: Жаксыгулова Д. Д

Семей 2015 жыл

Жоспар

Кіріспе

Негізгі бөлім

1. Регрессиялық талдаудың негізгі мақсатын анықтау
2. Регрессиялық талдау негізінде ШҚО жер салығы бойынша түсімнің бюджетке тиімділігін қарастыру

Қорытынды

Пайдаланылған әдебиеттер тізімі

1. Регрессиялық талдаудың негізгі мақсатын

анықтау

Регрессиялық талдау - регрессия теңдеуін анықтау және оның параметрлеріне статистикалық бағалауды енгізу. Регрессиялық талдау олардың параметрлеріне статистикалық бағалауды қосқанда регрессия теңдеуін анықтау нәтижесіне ие. Егер тәуелсіз шама немесе тәуелсіз айнымалылар белгілі болса, онда регрессия теңдеуі тәу елді айнымалының мәнін табады.

Регрессиялық талдаудың мақсаты - регрессия теңдеуін оның параметрлерінің статистикалық бағасын пайдалана отырып табу.

Регрессиялық талдау кезінде келесі негізгі мәселелер шешіледі:

1. Регрессия теңдеуінің жалпы түрін таңдау және регрессия параметрлерін анықтау.

2. Регрессия ішіндегі нәтижелік белгі мен факторлар арасындағы өзара байланыс дәрежесін анықтау, регрессия теңдеуінің жалпы сапасын тексеру.

3. Регрессия теңдеуінің әр коэффициентінің статистикалық маңыздылығын тексеру және олардың сенімділік аралықтарын анықтау.

Регрессиялық талдау экономикалық-статистикалық талдаудың келесі қадамы болып табылады және бір немесе бірнеше кездейсоқ шамалардың мәндеріне негізделетін кездейсоқ шаманың мәнін алдын ала айтуға мүмкіндік береді. Бұл мақсатқа Y тәуелді кездейсоқ шамасының (оны бұл жағдайда нәтижелік белгісі деп атайды) Х 1, Х2, . . . , Х М тәуелсіз кездейсоқ шамаларымен (оларды факторлар деп атайды) байланысын сипаттайтын аналитикалық өрнектің түрін анықтау арқылы ғана жетуге мүмкін болады. Y нәтижелік белгісінің Х 1, Х2, . . . , ХМ факторларымен байланыс формасын регрессия теңдеуі деп атайды. Таңдалған теңдеудің типіне байланысты сызықтық және сызықтық емес регрессияны ажыратады (мысалы, квадраттық, логарифмдік, экспоненциалдық және т. б. ) . Регрессия жұптық (қарапайым) және жиынтықтық болуы мүмкін, бұл өзара байланысқан белгілердің санымен анықталады. Егер екі белгілердің (нәтижелік және факторлық) арасындағы байланыс зерттелетін болса, онда регрессия жұптық деп аталады; бұл типке, мысалы, сату мен жарнамаға кететін шығын арасындағы байланысты зерттеу жатады. Егер үш немесе одан да көп белгілердің арасындағы байланыс зерттелсе, онда регрессия жиынтықтық (көпфакторлы) деп аталады, мысалы, егер тұтыну деңгейі, пайда, қаржылық жағдай және жанұя мөлшері арасындағы байланыс зерттелетін болса.

Регрессиялық талдаудың мақсаты және 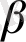бағалауларын анықтаудан тұрады. Мұнда U - дің мәні кіші болған сайын, есеп жеңіл болады. Егер кездейсоқ мүше мүдделі болмаған жағдайда түзудің орны анық көрсетілуші еді.

х 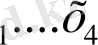х - тің 4 гипотекалық мәндері. Егер х пен у арасындағы қатыс нақты болса, онда у-тің сәйкес мәндері 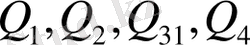нүктелерімен берілуші еді. Ал кездейсоқ мүшенің болуы у-тің мәнінің басқа болатынын көрсетеді. Суретте кездейсоқ шама 1-ші және 4-ші бақылауда оң, 2-ші, 3-ші бақылауда теріс болып, p 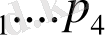нүктелерімен берілген. және 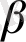параметрлері бағалау р нүктесіні арқылы теңдеудің орнын анықтаудан тұрады. Егер кездейсоқ шама болмаса, Р мен Q нүктелері сәйкес келіп, теңдеудің орнын оңай көрсетеді.

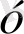және т айнымалылар мен тәуелсіз факторлар арасындағы байланысты регрессияның функциясы Y=f(X ₁ X ₂ , Х _м . . . , X), ретінде сипаттауға болады. Регрессия коэффициенті 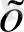айнымалысы нақты мәндерге ие болса, онда у айнымалысының орташа алғанда қандай мәнге ие болатынын көрсетеді.

2. Регрессиялық талдау негізінде ШҚО жер салығы бойынша түсімнің бюджетке тиімділігін қарастыру

Практикада, көптеген жағдайларда қандайда бір қорытындылы белгінің (нышан) бірнеше факторлық белгілерден тәуелділігін зерттеп, талдау жасау қажеттігі туады. Корреляциялық талдау статистикалық жиынтықтағы екі айн-малының арасындағы байланысты зерттеуге мүмкіндік береді. Бұл жағдайда математикалық-статистикалық модель көп айнымалылы регрессия теңдеуімен сипатталады. Мұндай регрессия көбейтілген деп аталады. Қазақстан Республикасының Қаржы министрлігінің мәліметтері негізінде есептелген кестесін және ШҚО жер қатынастары басқармасынан мәліметтері негізінде құрастырылған суретті негізге ала отырып, жер салығының жалпы салықтық түсімдер ішіндегі үлесін және пайдаға аспай жатқан яғни бұзылған жерлер мен айналымдағы жерлер арасындағы қатынасты, сондай-ақ жер салығы бойынша түсімнің бюджетке тиімділігін қарастырайық (1 кесте) .

1 кесте- Бюджеттің салықтық түсімдері (млн. теңге)

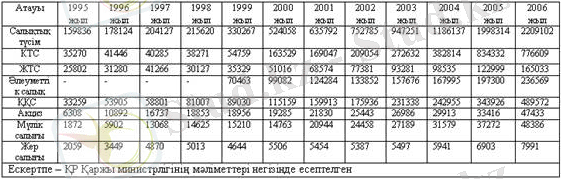
Енді келесі белгілеулерді енгізейік:

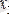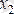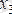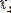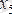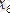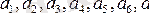- cалықтық түсімнің мәні, - корпорация табыс салығы, - жеке табыс салығы, - әлеуметтік салық, - қосылған құн салығы, - акциздер, - мүлік салығы, - жер салығы және - арқылы регрессия теңдеуінің параметрлерін белгілейік. Онда жеті белгісізді сызықтық регрессияның теңдеуін келесі түрде жазуға болады:

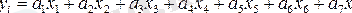(1)

Бұл теңдеудің параметрлерін бағала-ғанда әрбір -інші бақылауда -нәти-желік белгінің және -фак-торлық белгілердің мәндері бекітіледі. Ал регрессия теңдеуінің параметрлерін баға-лауды ең кіші квадраттар әдісінің көмегімен табамыз. Жиынтықтық регрессия жағдайында оны келесі матрицалық түрде қарастырған ыңғайлы болады:

2 кесте- Бюджеттің салықтық түсімдерінің матрицасы

Шығыс Қазақстан облыстық салық органдарының жұмысына корреляциялық және регрессиялық талдау жүргізу арқылы жүйелендіру міндеттері ғылыми терең зерттеулерді талап ететін бүгінгі таңдағы өзекті мәселердің бірі. Осы мәселені шешу үшін экономикадағы көп өлшемді статистикалық талдау әдістерін, мәселен корреляциялық және регрессиялық әдістерді пайдалануға болады .

Осы орайда экономикадағы көп өлшемді статистикалық талдау әдістерінің талаптарына сай келетін бастапқы мәліметтер базасын құрамыз. Мәсәлен, 2002-2005 жылдар барысындағы Шығыс Қазақстан облыстық статистика басқармасының мәліметтері кесте 1 арқылы анықталады. Мұндағы мәліметтер бюджеттің салықтық түсімдерінің матрицасы түрінде MS Excel электронды кестесінің А2:Н12 ұяшықтар блогына орналастырылады. Енді регрессия теңдеуінің параметрлерін бағалау үшін ең кіші квадраттар әдісін қарастырамыз, ол үшін алдымен

Келесі белгілеулер енгізейік:

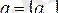
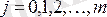- параметрлерді бағалау векторы,

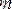- белгісіз параметрлер саны;

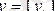
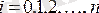- тәуелді айнымалылардың мәндерінің векторы,

- бақылаулар саны;

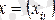- өлшемі 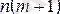болатын тәуелсіз айнымалылардың мәндерінің матрицасы;

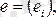- параметрлері бағаланған теңдеудің қателіктер векторы.

Параметрлері бағаланған регрессия теңдеуі келесі түрде жазылады:

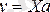(2)

Сызықтық (1) моделі векторлық түрде келесідей жазылады:

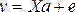(3)

Ауытқулар квадраттарының қосындысы:

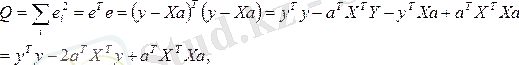(4)

мұндағы - транспозициялау амалының белгісі, яғни берілген матрицаның жатық жолдары транспозиция-ланған матрицаның тік жолдарының орынына, ал тік жолдары жатық жолдарыныңң орынына жазылады.

Енді -ді 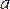бойынша дифференциалдасақ келесі теңдікті аламыз

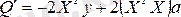(5)

Ары қарай 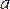- бағалау векторын анықтау үшін туындыны нолге теңестірсек келесі теңдікті аламыз:

,

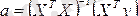. (6)

Жоғарыда келтірілген тәсілмен алынған 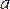- бағалауын ең кіші квадраттар әдісінің бағалауы деп атайды. Егер (1) регрессия теңдеуіне қолдансақ коэффи-циенттер матрицасы келесі түрде болады:

Енді жоғарыда келтірілген ең кіші квадраттар тәсілін MS Excel электронды кестесінің А2:Н12 ұяшықтар блогына орналастырылған бюджеттің салықтық түсімдерінің матрицасына қолданамыз.

MS Excel электронды кестесінің «Регрессия» функциясы сызықты регрессия теңдеуінің параметрлерін есептеуге және талдау жасауға арналған. Берілген функцияның негізгі терезесінде келесі параметрлер енгізіледі.

1. Енгізілген аралық Y - мұнда берілген тәуелді айнымалылар орналасқан ұяшықтар енгізіледі. Олар бір тік жолда орналасуы қажет.
2. Енгізілген аралық X - мұнда факторлық тәуелсіз айнымалылар орна-ласқан ұяшықтар енгізіледі. Енгізілетін тік жолдардың ең үлкен саны 16. Қарастырылып отырған есепте тік жолдар саны салықтың түрлерінің санына тең, яғни 7 тік жол болады.
3. Сенімділік деңгейі - егер берілген 95 пайыздан басқа сенімділік қажет болса ғана бұл жерге белгі қойылады. Қойылған сенімділік мөлшері детерминация коэф-фициентінің және регрессия коэф-фициенттерінің мәнділігін бағалау үшін қажет.
4. Константа ноль - егер регрессия сызығы координаталардың бас нүктесінен өтуі қажет болса ғана бұл жерге белгі қойылады.
5. Шығу аралығы - мұнда шығу интервалының қай жерге орналасуы қажет екені көрсетіледі.
6. Қалдықтар - егер шығу интервалында қалдықтар тік жолын шығару қажет болса, онда осы жерге белгі қойылады.
7. Стандартталған қалдықтар - егер шығу интервалында стандартталған қалдықтар тік жолын шығару қажет болса, онда осы жерге белгі қойылады.
8. Қалдықтар графигі - егер шығу бетіне қалдықтардың факторлық белгі-сіздерден тәуелділігінің нүктелік график-терін шығару қажет болса, онда осы жерге белгі қойылады.
9. Іріктеу графигі - егер шығу бетіне Y айнымалысының мәндерінің X - факторлық тәуелсіз айнымалыларынан тәуелділігінің нүктелік графиктерін шығару қажет болса, онда осы жерге белгі қойылады.
10. Қалыпты ықтималдылық графигі (график нормальной вероятности) - егер шығу бетіне бақыланушы Y айны-малысының мәндерінің автоматты түрде құрылатын персентиль аралықтарынан тәуелділігінің нүктелік графиктерін шығару қажет болса, онда осы жерге белгі қойылады.

Бұл аталған параметрлерді енгізгеннен кейін 1 суретте келтірілген негізгі терезеде ОК баспасын іске қосамыз.

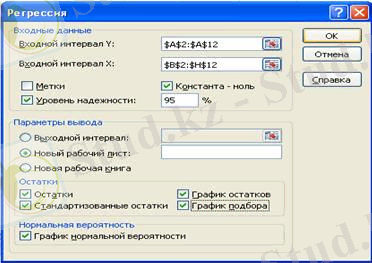
1 сурет - «Регрессия» функциясының негізгі терезесі

Онда есептелген қорытынды қажетті параметрлерді қарастырамыз.

3 кесте - Есептелген параметрлер кестесі.

Бұл алынған параметрлер келесі статистикалық көрсеткіштерге сәйкес келеді: жиынтықтық R - корреляция коэффициентіне, R-квадрат - детерминация коэффициенті R ² , стандарт қателік - қалдықты стандарт ауытқу

.

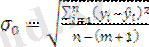Келесі есептелетін шамалар дисперсиялық талдау параметрлері болып табылады.

4 кесте -Дисперсиялық талдау параметрлері

5 кестеде дисперисиялық талдауға қажетті шамалар мәндерін алдық. Келесі қадамда ең негізгі қажетті регрессия теңдеуіне қажетті регрессия коэффи-циенттері, стандарт қателік және статистиканың басқа да параметрлері анықталады.

5 кесте -Регрессиялық талдау параметрлері

Статистикалық талдауда ең қажетті шамалардың бірі қалдықтар қорытын-дылары болып табылады. Сондықтан келесі кестеде қалдықтар қорытындысы келтірілген.

6 кесте -Қалдықтың қорытындысы

Соңында, ықтималдықтарды қоры-тып персентильдер шамалары көрсетілген кестені аламыз және 3-ші және 4-ші суреттерде келтірілген қалдықтар және қалыпты таралу графигін аламыз.

3 сурет - Қалдықтар графигі

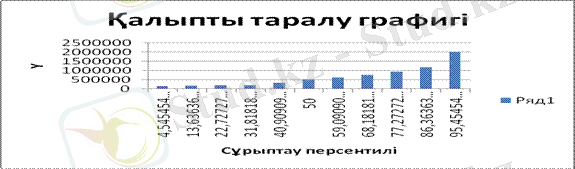
4 сурет - Қалыпты таралу графигі

Жоғарыдағы барлық талдауларды пайдаланып келесі регрессия теңдеуін аламыз:

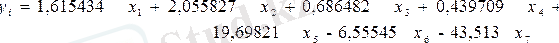
Бұл теңдеуден көретініміз - cалықтық түсімнің мәніне - жер салығы мөлшерінің өте аз ықпалының бар екені, яғни жер салығын тұрғылықты зерттеп, оның мөлшерін көбейту үшін қандай шаралар қолдануға болатынын анықтаған жөн. Ол үшін жер салығының мөлшері қандай негізгі факторларға тәуелді екенін анықтау қажет. Бұл қойылған мақсатты орындау үшін жер салығына қолданылмай жатқан жерлердің, әсіресе жыл аяғына бұзылған жерлердің және оларды өңдеу үрдістерінің әсерін талдау қажет.

Сондықтан енді жер салығына корреляциялық талдау жасайық. Математикалық-статистикалық моделдеуді қолдану үшін келесі белгілеулер енгіземіз:

- жер салығының шамасы, млн. теңге

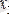- жыл аяғына бұзылған жерлер, га

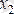-жыл аяғына бұзылған жерді өңдеу, га

Енді қажетті бастапқы мәліметтерді келесі Шығыс Қазақстан облысының статистикалық орталығынан алынған мәліметтер бойынша құрылған келесі кестеге орналастырамыз.

8 кесте - Бастапқы мәліметтер кестесі

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс