Іздеу есептерінің шешілімі. Іздеу: қайтару арқылы теріп алу жайлы

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

СӨЖ

Тақырыбы: Іздеу есептерінің шешілімі. Іздеу: қайтару арқылы теріп алу.

Орындаған: Мұратқанова Ә. Е. Т-341

Тексерген: Болсынбекова Ш. Ж.

2015 жыл

Жоспар:

1. Ақпараттық іздеудің қарапайым есебі

2. AVL-ағаштар және толыққа жуық бинарлы ағаштар.

Бинарлы ағаштармен жасалатын стандарты операциялар.

8. Бинарлы ағашта кесте құру және оның ерекшеліктері.

1. Ақпараттық іздеудің қарапайым есебі

Іздеу әдістері және іздеумен байланысты есептерді зерттеу мәселесі, зерттеулердің жеке және қызықты бағыттарының бірі. Қарапайым ақпаратты іздеу есебін қарастырайық. Мысалы, университеттің мех-мат факультетінің барлық 1-ші курс студенттерінің ішінен берілген РНН1 арқылы немесе сынақ кітапшасының нөмері арқылы осы нөмірге несеае РНН-ге сәйкес студентті табу қажет болсын. Осы қойылған есеп қарпайым шешімге ие бола алады. Мысалы, қарапайым тізбектеп қарастыру әдісін қолданып, студенттер тіркелген кестеден тізбектеп барлық студенттердің РНН-нің ішінен берілген РНН-ді салыстыра тексере отырып табуға болады. Ал егер осындай іздеуге үлкен мегеполистің деректер қорынан берілген РНН-ді іздеп табу қажет болса, және іздеуді осындай қарапайым жолмен ұйымдастырсақ, онда өте көп уақыт алатыны айқын. Мұндай әдіспен шешу жолы қабылданбайды.

Сөйтіп, А массиві берілсін. Берілген А массивінің элементтерінің табиғаты кез-келген болсын. Және Р массиві берілсін, массивтің элементтерінің табиғаты сан болсын. А массивінің кез-келген ai элементіне Р массивінің элементі рі бір мәнді сәйкестікпен тағайындалсын. Оған қоса P массивтің элементтерін А массивтің элементтерінің белгісі немесе кілттері деп атайды. Формальді түрде қойылған қарапайым ақпаратты іздеу есебінің қойылымын келесідегідей тұжарымдауға болады: р* кездейсоқ кілт берілсін. А массиві элементтерінің ішінен кілті р*-ға тең элементті табу қажет немесе А массивінің элементтері ішінен р* сәйкес кілтті элемент жоқ екені анықталу қажет. Қойылған есепті математикалық тұрғыдан теориялық жолмен шешсек, онда Р кілттер жиынында анықталған қандайда бір функция түзуді қажет етеді. Түзілген функция кілті р* сәйкес А массивінің элементінің нөмерін бір қадам ішінде қайтаруы мүмкін, егер де ондай бар болса. Қойылған есепті шешудің тағы бір жолы бұл комбинаторикалық жол. Бұл жолдағы айғақты процедура ретінде іздеуді тізбектеп немесе басқаша айтқанда сызықты іздеу негізінде ұйымдастырады. Тізбектеп іздеуде орташалап алғанда саны салыстыруларды қажет етеді. Бүтін мәнді оң анықталған аргументтері натурал сан болып келетін функциялар болсын. Егер барлық үшін шарты орындалатындай оң анықталған с константасы n0 нөмірі табылатын болса, онда функциясы О-үлкен -нен деп аталады және түрінде жазылады. Егер барлық үшін шартты орындалатындай оң анықталған с константасы n0 нөмірі табылатын болса, онда функциясы -үлкен -нен деп аталады және түрінде жазылады. Н Н -бүтін мәнді оң анықталған аргументтері натурал сан болып келетін функциялар болсын. Егер барлық үшін шартын қанағаттандыратындай оң анықталған константалары және нөмері табылатын болса, онда - Н - нен дейді және = () түрінде болады. Иии -нотациясында 1 ғана функция, бұл жағдайда функциясы, қандай да бір n0 нөмірден бастап функциясы үшін жоғары және төменгі шегі болып табылатынын айта кету маңызды. Компьбтерлік жүйелерде көп тараған екілік іздеу алгоритмінің салыстыру санының күрделілігінің жоғарыдан бағасы жуық. Екілік іздеу алгоритмді қолдануда берілген бастапқы массив х1, х2, . . . , х п реттелген бөлу қажет. Массивтің реті мысалға, өспелі х1 х2х п немесе кемімелі х1 х2 . . . х п болу мүмкін. Бастапқы массивтің элементтер саны немесе элементтерінің мәндері уақыт айналымынан өзгеріп отыруы мүмкін, осыған орай реттеу алгоритмдерінің тиімділігі мәселесінің ролі арта түседі. екілік іздеуді ұйымдастыратын алгоритмнің стандартты нұсқасы төменде көрсетілген.

function BinSearch(b, p*, n) ;

….

begin l:=0;

h:=n;

while l<=h do

begin

m:=(l+h) div2;

if b[m] p* then h:=m-1

else

begin

binsearch:=m;

exit;

end;

end;

binsearch:= -1;

end; //-1 мәнінің қайтарылуы р* -ның массивте табылмағанын көрсетеді.

2. AVL-ағаштар және толыққа жуық бинарлы ағаштар.

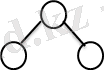
AVL ағаштары. Бинарлы ағаштардың бұл класы алдыңғы жағдайдағымен салыстырғандағы тұрғызу алгоритмі күрделі болғанымен маңызды позитивті қасиеттерге ие болады. Бұл типті ағаштар көзге бейсимметриялы көрінуі мүмкін, бірақ оларда ұзын бұтақтар жоқ. Мұндай ағаштың түбірінен шыққан бұтақтың максималды ұзындығы, мұнда c аспауы тиіс. AVL ағаштарды көбіне баланстандырылған ағаштар деп атайды. Бұтақ ұзындығы деп осы бұтаққа тиісті ең ұзын жолдың ұзындығы алынады. Ағаш төбесі балансы деп берілген төбе/ден шығатын оң ж/е сол бұтақ/ ұзындықтарының айырмасын айтады. Егер ағаштың әрбір төбесі үшін баланстың абсолют мәні 1-ден артық болмаса, онда ағашты баланстандырылған (AVL) ағаш д. а. n элементтен тұратын массив бойынша тұрғызылған AVL ағаштағы ең ұзын бұтақтың ұзындығын бағалайық. Бұл үшін санын белгілейміз, алдымен максималь ұзындығы l-ға тең бұтақтары бар AVL ағаштар жиынын қарастырамыз. Осы ағаштардың ішінде төбелер саны минимум болатындары да бар. Ары қарай бұл AVL ағаштарын минималды деп атаймыз. Енді мына функцияны қарастырайық. n(l) -AVL ағашындағы төбелердің минималь саны, бұтақтарының максималь ұзындығы тең. l=0, 1, 2, 3, 4 және 6 үшін минималь AVL ағаштарының мысалын келтірейік.

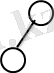
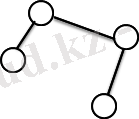
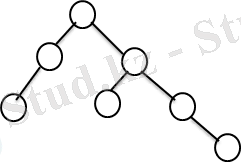
2. 5. сурет: a) n(0) =1, l=0 б) n(1) =2, l=1 в) n(2) =4, l=2 г) n(3) =7, l=3

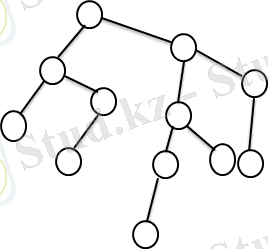
2. 6. сурет n(4) =12, l=4

2. 7. сурет n(5) =20, l=5

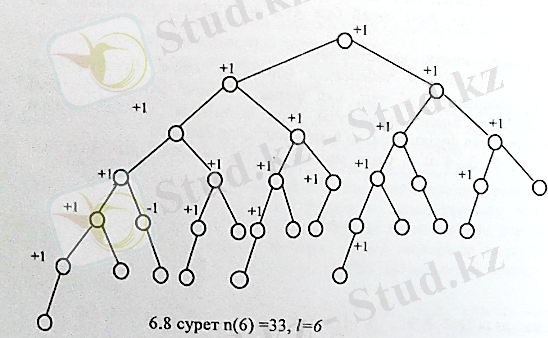
Сәйкесінше AVL ағашына элемент қосуға жұмсалатын уақыт жаман жағдайда тең. Келтірілген баға басқа түсініктерден шығады, атап айтсақ Фибоначчи санын бағалауы белгілі.

AVL ағашында іздеу үшін орташа жағдай тартымды көрінеді, оның бағалау түрі мынадай, мұндағы

яғни, минималды мүмкіндіктен бар болғаны 4% нашар.

Толыққа жуық бинарлы ағаш. Бинарлы ағаштың өсу нүктесі деп вакантты бағыт б/ша жаңа қабырға тұрғызуға болатын төбені айтады.

2. 1. сурет 2. 2. сурет

Бинарлы ағашты толықтау дейміз, егер онын барлық өсу нүкте/і осы ағаштың тек соңғы ж/е соңғының алдындағы деңгей/де орналасса.

Кейде мұндай ағашты толықтау баланстандырылған деп те атайды. Егер толықтау ағашта m деңгейінен жоғары төбелер жоқ десек, онда элементті іздеуге қажетті салыстырулардың максималды саны былай бағаланады, яғни, толықтау ағаш үшініздеу eceбi оптималды минималды уақытта шешіледі, яғни салыстыру саны минимадды болады. Толықтау ағаш тұрғызу алгоритмi курделі емес, бipaқ бұл ағаштардың айтарлықтай кемшіліетері бар. Егер массив статикалы болса, яғни элементтер саны да, элементің өзi де өзгермесе, онда толықтау ағашты іздеуге қолдану негізді болып табылады. Мұндай ағашты ұйымдастыруға бip рет уақыт жұмсаса, ары қарай тек іздеу eceбi ғана жүргізледі және ал тиімді болады. Егер массивтің элементтері периодты турде өзгерсе немесе қосылса н/е алынатын болса, онда бұл басқа бip мәселе.

Дәстүрлі түрде 6 элементтен тұратын массивті және оның толықтау ағашын қарастырайық.

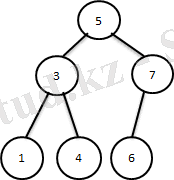
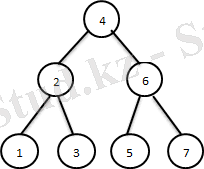
бip ғана «2» элементін қосу ағашты қайта құруды к/к етеді, бұл кезде массивтің тек бip элементі ғана өз орнында қалды (4 сурет) .

Бастапқы массив бойынша толықтау ағаш тұрғызу алгоритмі қарапайым болғанымен, бұл типті ағаштарды динамикалық массивтерге қолдану тиімділігі өте төмен болады, себебі жоғарыда көргеніміздей массив аз ғана өзгеріске түскен кезде ағашты айтарлықтай немесе толық қайта құру қажет болады.

3. Бинарлы ағаштармен жасалатын стандарты операциялар.

Ағаштарды телу арнайы операцияларын пайдаланып, қайталанба айналымдардың тиімді екендігін көрсететін жолмен жүруімізге болады. Мысалы, ағаштың симметриялы айналымында бұл ағашты оң жақтан симметриялы телінген ағаш түрінде құруға болады.

Штрихтелінген бағыттауыш жіп деп аталады және ол кері бағытты қозғалыс кезінде, симметриялы айналымда келесі кезекте болып өтетін түпкі ағашты көрсетеді.

Енді симметриялы телінген ағашта, симметриялы айналуда алдыңғы сәйкес төбеге бір қосымша ұяшықты бағыттаушы жіп ретінде қосып, стекті пайдаланбай-ақ, іске асыруға болады.

Тура ретпен орналасқан айналымдар үшін оң жақтан тура (түзу) телінген ағаштарды қосуға болады. Бағыттауыштар бұл ағашта түпкі ағашты емес, енді тура ретті айналымдағы келесі кезекте болатын төбені көрсетеді. Сондай-ақ, кері реттегі айналымға да қатысты. Енді жоғарыда көрсетілген екі суретте де бағыттың айырмашылығын анықтау пайдалы болады. Сонымен қатар, мұнда ағаштардың сол жақтан симметриялы және сол жақтан тура телінген класстарын еске сақтаған жөн. Сол жақтан симметриялы телінген ағаш жағдайында, әрбір сол жақтағы бағыттауыш ағаштың сәйкес төбесіндегі симметриялы ретте жүргізілетін, берілген түйіннің алдыңғысына сілтеме жібі болады. Тура осылай, сол жақтан тура телінген ағаш үшін ағаштың сәйкес төбесінде әрбір сол жақтағы бағыттауыштың, ағаштың тура бағытындағы өзінің алдыңғысына сілтеме жібі болады.

Бинарлы ағаштарға жүргізілетін операциялар. Олардың кейбіреуін, яғни бинарлы ағаштың телінуі мен айналымын біз жоғарыда қарастырып өткенбіз. Жаңа операциялар тізімін микрооперациялардан бастауға болады, олардың ішінен келесі операцияларды ерекшелейік:

1. copy(t, v’) - бізге белгілі тура симметриялы және кері реттегі айналымдардың көмегімен орындалатын бинарлы ағаштың операциясы. Бұл операцияның орындалуының нәтижесі бастапқы бинарлы ағаштың көшірмесі. Copy(t, v’) функциясы t-ағашының көшірмесінің түбірі - V’-түйініне көрсеткішті қайтарады.
2. ecv(t1, t2) - аргументтері екі бинарлы ағаш болатын, ал нәтижесі, егер эквиваленттілік орындалса true мәнін, кері жағдайда false мәнін қабылдайтын эквиваленттілік операциясы. Мұндағы “эквмваленттілік” термині бинарлы ағаштар үшін, бұл операция орындалмай тұрып, алдын-ала анықталып, және ситуация барысында өзгертіліп қолданылады. Мұндай жағдайда, мысалы үшін бір бинарлы ағаштың көшірмелері жөнінде айтуға болады.
3. subtree(v, t) - операциясы түбірі t- ағашының қандай да бір V- төбесі болатын, t- ағашының ішкі ағашын қайтарады. Дәлірек айтсақ, subtree операциясы сілтемені v- түйініне қайтарады. Енді келесі операцияларды қарастырсақ:
4. inf(v, t’) йункциясы t- ағашының v- түйінінің құрамын толығымен қайтарады.
5. right_des (v, t’) left_dess (v, t) функциялары t- ағашының v-төбесінің сәйкес тікелей оң және сол жақ ұрпақтарына көрсеткіштерді қайтарады, әрине егер олар бар болса. Бұл көрсетілген операция типімен басқа да операциялар байланысты, дәлірек айтсақ, set_left(v, v’, t) және set_right(v, v’, t) . Мұндағы v t- ағашының сәйкесінше t- ағашында сол және/немесе оң тікелей ұрпақтары болмайтын түйіні set_left(v, v’, t) операциясы V’төбесі болатын, яғни V’төбесіне көрсеткіш болатын сол жақ тікелей ұрпақты құрады және осы төбеге сілтемені қайтарады. Ал set_right(v, v’, t) операциясы V’- төбесіне көрсеткіштің рөлін атқаратын t-ағашының v-төбесінің оң жақ тікелей ұрпақтарын құрайды және сәйкесінше V’-төбесіне сілтемені қайтарады.
6. anc(V, t) функциясы t-ағашында V-төбесінің тікелей тегіне көрсеткішті қайтарады, егер олар табылса.
7. L_nabour (V, t) функциясы t- ағашында V-төбесінің сол жақ көрші төбесіне көрсеткішті қайтарады.
8. r_nabour (V, t) функциясы t- ағашының V-төбесінің сәйкес оң жақ көршісіне көрсеткішті қайтарады.
9. change (V, V’, t) t- ағашындағы V- түйінімен V’ түйінін ауыстырады (алмастырады) . Бұл операция макрооперацияға қарағанда дербес болып табылады.
10. change (V, V’, t) t- ағашындағы түбірі V түйіні болатын ішкі ағашты, t’-ағашындағы түбірі V түйіні болатын ішкі ағашпен алмастырады, кейбір жағдайларда t=t’.

Маңызды және сондай-ақ бастапқы операция болып табылатын make tree (V, V’, V”, t) операциясы t- ағашын V’ түйініндегі түбірмен және V’ түйінінен шығатын V’-сол және V’-оң жақ ішкі ағаштар түбірлеріне бағыттаушылармен(әрине, егер олар бар болса) береді. Егер V’ түйінінің оң(cол) жақ тікелей ұрпақтарын болмаса, онда V-төбесінің сәйкес ұясына nill жазылады. Ал make_tree функциясы түбірге көрсеткішті - V түйінін қайтарады.

Бинарлы ағаштарға жиі қолданылатын операция болып ins(V, t) операциясы табылады, ол t- ағашына жаңа V түйінін кірістіру операциясы. Бұл операция қарапайым бинарлы ағаш үшін жоғарыда көрсетілген мысалдар бойынша ешбір қйындықсыз орындалады. Алайда, басқа да арнайы бинарлы ағаштар класы үшін, толықтау ағаштар үшін және қызықтысы AVL класының ағаштары үшін, н/е хип-құрылым үшін бұл операцияның өзіндік ерекшеліктері мен қолайсыздықтары бар. Қарапайым ағаштар үшін, әрине егер олар бос болмаса ins(V, t) функциясы сілтемені v-төбесінің түпкі ағашына қайтарады, ал оның информациялық өрісі жаңа бір төбеге сілтеме түрінде жазылады, яғни V-ға. Тағы да басқа осындай басқа бір операция del(V, t) ол t-бинарлы ағашынан V түйініндерін өшіреді. Бұл операция ins(V, t) -кірістіру операциясына қарағанда толық ж/е AVL-ағаштары клас/ын айтпағанда, қарапайым ағаштар үшін де комментарийлерді қажет етеді. del(V. t) -функциясы v-төбесінің тікелей негізінде (“атасына”) сілтемені қайтарады, ал информациялық өрісте жаңа ұрпақтың төбесіне сілтеме жазылады, әрине егер ол бар болса.

4. Бинарлы ағашта кесте құру және оның ерекшеліктері.

Идентификатор кестесінде элементті іздеу арқылы уақыт қысқартуға болады, белгілі уақытты үлкетпей-ақ, оны толтыру керек болады. Ол үшін кесте ұйымдастырудан үзіліссіз массив туріндег ұймдастырудан бас тарту керек.

Кестені құру әдісі бар. Кесте бинарлық ағаш формасын көрсетеді.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс