Тізбекті стерженді жүйелердің сенімділігін есептеуде дельта-функция мен ықтималдық таралуларды қолдану


Қазақстан Республикасының Білім және ғылым министрлігі Шәкәрім атындағы Семей мемлекеттік университеті
«Сызықты автоматты реттеу жүйелері» пәнінен
СӨЖ
Тақырыбы: Дельта-функция
Орындаған: Қайсар Д. Б.
Тобы: АУ-401С
Тексерген: Секербаева А. Б.
Семей 2015
Жоспар:
- Дельта-функция туралы жалпы мағлұмат
- Қолданылған әдебиеттер
Тізбекті біріккен стержендердің сенімділігін есептеу үшін әдетте «әлсіз буын» үлгісін қолданады. Осы үлгі бойынша статикалық анықталған стержендік жүйе немесе шынжыр есептелінеді, олар
 элементтерінен тұрады. Егер
элементтерінен тұрады. Егер
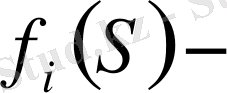
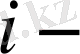 элементтегі кернеудің таралу тығыздығы болсын. Шынжыр үшін кернеу барлық элементтерде бірдей болады; стержендік жүйелер үшін кернеулердің таралу заңдары бірдей, бірақ параметрлерімен ажыратылады. Егер де шектік кернеудің таралу функциясын
элементтегі кернеудің таралу тығыздығы болсын. Шынжыр үшін кернеу барлық элементтерде бірдей болады; стержендік жүйелер үшін кернеулердің таралу заңдары бірдей, бірақ параметрлерімен ажыратылады. Егер де шектік кернеудің таралу функциясын
 арқылы белгілесек, онда
арқылы белгілесек, онда
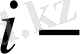 элементінің қирамау ықтималдығы, шарт бойынша ондағы кернеу
элементінің қирамау ықтималдығы, шарт бойынша ондағы кернеу
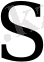 - ке тең болғанда,
- ке тең болғанда,
 болады. Бұл өрнекті кернеулердің барлық мүмкіндік мәндерінде интегралдай отырып,
болады. Бұл өрнекті кернеулердің барлық мүмкіндік мәндерінде интегралдай отырып,
 элементінің сөзсіз қирамау ықтималдығын табамыз
элементінің сөзсіз қирамау ықтималдығын табамыз
(1)
Жүйелердің тоқтамай жұмыс жасау ықтималдықтары сәйкес ықтималдықтардың көбейтінділерімен анықталатын формула бойынша жүйенің тоқтамай жұмыс жасау ықтималдығын анықтаймыз
(2)
Егер кернеу элементтерде кездейсоқ болмаса, онда
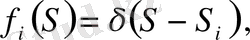
(3)
мұндағы
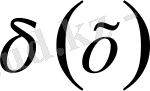 - Дирактың дельта функциясы.
- Дирактың дельта функциясы.
Егер кернеулер элементтерде бірдей болса, онда (3) орнына аламыз
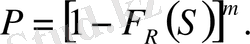 (4)
(4)
Кернеулер барлық элементтерде бірдей болсын, бірақ кездейсоқ шама болып табылса, онда (4) өрнегін шартты ықтималдық деп ұғып, оны былай жазуға болады
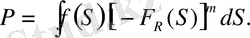 (5)
(5)
Бұл формуланы (1) - дан оңай аламыз,
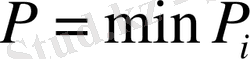 ,
,
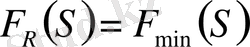 деп, мұнда таңдаманың ең кіші мәнінің таралу функциясы
деп, мұнда таңдаманың ең кіші мәнінің таралу функциясы
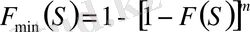 . (6)
. (6)
Егер шектік кернеу Вейбулл таралуына бағынса
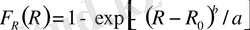 ,
,
онда (3) - (5) формулаларының орнына, сәйкесінше, аламыз
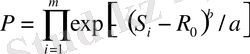 ;
;
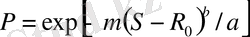 ;
;
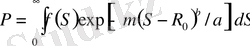 . (7)
. (7)
Енді стержендер әртүрлі материалдардан жасалған деп санаймыз. Онда (2) және (3) формулаларының жалпылауымен сәйкесінше келесі өрнек анықталады
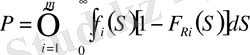 ;
;
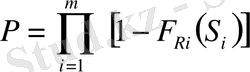 ; (8)
; (8)
ал (5) формуланың орнына, аламыз
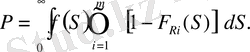 (9)
(9)
Енді стержендердегі әсер етуші және шектік кернеулер қалыпты заңмен таратылсын. Онда тоқтамай жұмыс жасау ықтималдығы мына формула бойынша анықталады
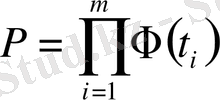 , (10)
, (10)
мұндағы
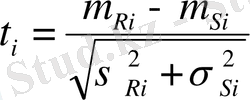 немесе
немесе
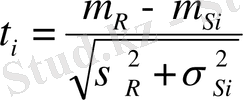 .
.
Егер стержендердегі әсер ететін және шектік кернеулер логарифмді қалыпты таралуға ие болса, онда (10) - ші өрнекті қайта аламыз. Ықтималдықтарды қосып, жүйенің толық сенімділігін анықтау арақатынасын ескеріп, сонымен қоса логарифмді қалыпты таралу параметрлері және кездейсоқ шамалардың сандық сипаттамалары арасындағы тәуелділікпен, табамыз
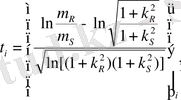 ,
,
мұндағы
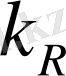 ,
,
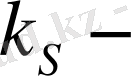 вариация коэффициенттері.
вариация коэффициенттері.
Көбінесе тізбекті біріккен стерженді жүйенің сенімділігін анықтау үшін (5) - ші формула қолданылады. Ол барлық стержендерде кернеулер бірдей деп жобалайды, бірақ олар кездейсоқ, ал барлық стержендердің көтеру қабілеттіктері бірдей. Осы шарт бойынша шынжырлар, тісті дөңгелектер жұмыс жасайды, оларда буындар мен тістер элементтер болып саналады. Бұл формулалар бойынша сенімділікті анықтау жалпы жағдайда сандық интегралдауды қажет етеді және
 көп болғанда тек ЭЕМ қолданылуы керек.
көп болғанда тек ЭЕМ қолданылуы керек.
Егер бұл формулаларда кернеу қалыпты заңмен таратылса, онда жүйенің сенімділігін анықтау үшін жуықтау әдісін қолдануға болады, ол [1] - ші жұмыста келтірілген. Әдістің мақсаты жүйенің көтеру қабілеттілігінің таралу заңы қалыпты заңмен былай жуықталады, яғни жүйенің көтеру қабілеттілігінің диапазонындағы төменгі мәндерінің нақтылығына жақын болуы, осы мәндер жүйенің сенімділігін анықтайды.
Бұл идея келесі түрде болады:
- Бекітілген кернеулердің екі мәнін қабылдаймыз:
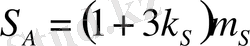 ,
,
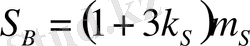 .
.
- Осы кернеулердегі тоқтамай жұмыс жасау ықтималдығын анықтаймыз
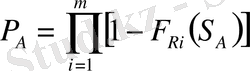 ,
,
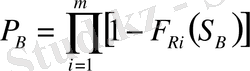 ;
;
немесе
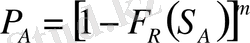 ,
,
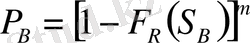 .
.
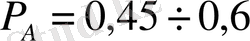 ,
,
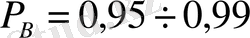 болуы мүмкін. Егер бұл аралыққа түспесе
болуы мүмкін. Егер бұл аралыққа түспесе
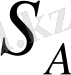 және
және
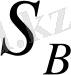 - ны сәйкес жағына қарай өзгертеміз.
- ны сәйкес жағына қарай өзгертеміз.
- Анықталған ықтималдықтарға сәйкес келетін қалыпты таралудың, квантильдерін табамыз.
- Жүйенің көтеру қабілеттілігінің таралу заңының параметрлерін, қалыпты заңмен жуықтаймыз. Сонымен
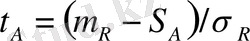 ,
,
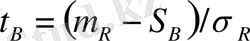 ,
,
онда осыдан аламыз
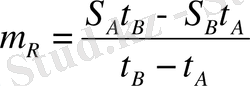 ,
,
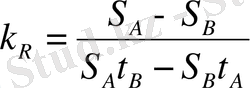 . (11)
. (11)
- Енді жүйенің сенімділігін мына формула бойынша анықтаймыз
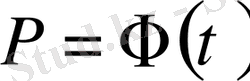 ,
,
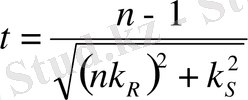 ,
,
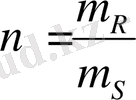 . (12)
. (12)
(9) формула бойынша ЭЕМ - да салыстыру есептері жуықтау әдісімен көрсетіледі, яғни оның дәлдігі жүйенің сенімділігін есептеуде инженерлік есептер үшін жеткілікті, олардың көтеру қабілеттілігінің вариация коэффициенті 0, 15 - тен аспайды, ал элементтер саны 15 - тен аспайды.
Элементтегі шектік кернеудің қалыпты заңмен таралу жағдайында
 бірдей элементтен тұратын шынжырдың көтеру қабілеттілігі (6) таңдамасының ең аз мүшесінің таралуына сәйкес келеді.
бірдей элементтен тұратын шынжырдың көтеру қабілеттілігі (6) таңдамасының ең аз мүшесінің таралуына сәйкес келеді.
 үлкен болған сайын, бұл заң қалыптыдан көп ажыратылады.
үлкен болған сайын, бұл заң қалыптыдан көп ажыратылады.
 ұлғайған сайын математикалық үміт пен тұрақты кішірейеді. Экстремалды таралу теориясы бойынша дәлелденген бұл таралу,
ұлғайған сайын математикалық үміт пен тұрақты кішірейеді. Экстремалды таралу теориясы бойынша дәлелденген бұл таралу,
 өскен сайын екі еселенген экспоненциялдыға жақындайды.
өскен сайын екі еселенген экспоненциялдыға жақындайды.
Бұл жағдайда жүйенің сенімділігін анықтау үшін басқа дәл және қарапайым әдіс қолдануға болады. Әдістің идеясы жүйенің көтеру қабілеттілігінің таралу заңын қалыпты заңмен жуықтаумен қорытындыланады. Бұл таралулар орта бөлігіндегіндей аз ықтималдық облысына да жақын болуы керек, яғни осы облыс жүйенің сенімділігін анықтайды. Сонымен таралуды жуықтайтын параметрлерді анықтаған кезде медианды мәндегі және жүйенің көтеру қабілеттілігінің мәнінің таралу шартының тепе - теңдігі ұсынылады, ол жүйенің тоқтамай жұмыс жасау ықтималдығына сәйкес келеді. Жуықтаудан кейін жүйе сенімділігін (12) - шы формула бойынша анықтайды.
Элемент беріктігінің қалыпты таралуының параметрлерін
 ,
,
 деп белгілейміз. Жүйенің көтеру қабілеттілігінің математикалық үміті мен тұрақтысы элементтерге қарағанда төмен екенін ескеріп, былай жазуға болады
деп белгілейміз. Жүйенің көтеру қабілеттілігінің математикалық үміті мен тұрақтысы элементтерге қарағанда төмен екенін ескеріп, былай жазуға болады
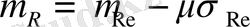 ,
,
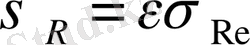 .
.
мұндағы
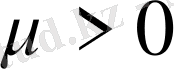 және
және
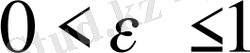 -
-
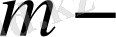 ге тәуелді кейбір коэффициенттер, ал
ге тәуелді кейбір коэффициенттер, ал
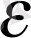 сонымен бірге, жүйе сенімділігінің квантильіне де тәуелді
сонымен бірге, жүйе сенімділігінің квантильіне де тәуелді
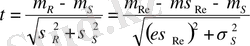 . (13)
. (13)
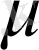 мен
мен
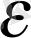 мәндері
мәндері
 жұмысында есептелген және бұл параметрлердің өзгерулерінің графиктері мен кестелері құрылған. Есептеуді автоматтандырудың қажеттігін ескеріп, оларды өрнекпен жуықтаймыз
жұмысында есептелген және бұл параметрлердің өзгерулерінің графиктері мен кестелері құрылған. Есептеуді автоматтандырудың қажеттігін ескеріп, оларды өрнекпен жуықтаймыз
 болғанда
болғанда
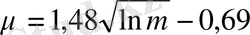 ,
,
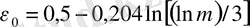 (14)
(14)
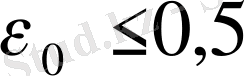 болғанда
болғанда
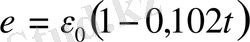 ;
;
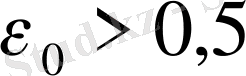 болғанда
болғанда
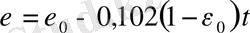 .
.
(13) формуласын вариация коэффициенттері арқылы жазуға болады.
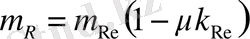 ;
;
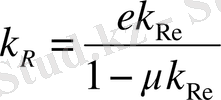 ;
;
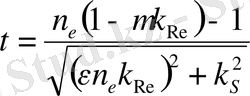 , (15)
, (15)
мұнда
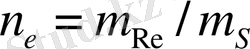 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz