Материялық нүкте динамикасы: қозғалыстың дифференциалдық теңдеулері және алғашқы интегралдар


ЖОСПАР
МАТЕРИЯЛЫҚ НҮКТЕ ДИНАМИКАСЫ1
Материялық нүкте қозғалысының диференциалдық теңдеулері. 1
МАТЕРИЯЛЫҚ НҮКТЕ ДИНАМИКАСЫ
Динамикада материялық нүктелер мен материялық денелердің қозғалыстары оларды болдыратын физикалық себептермен (күштермен) тығыз байланысты қарастырылады. Денеге түсірілген күштер мен олардың әсерлерінен болатын қозғалыс арасындағы тәуелділікті зерттеу, сүйтіп қозғалыстың жалпы заңдылығын табу мәселелері қаралады.
Динамиканың негізгі заңы.
Ньютонның II-заңы. Материялық нүктеге әсер етуші күш осы нүкте үдеуімен бағытталады және шамасы үдеуге пропорционал болады
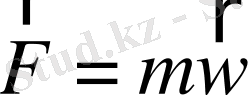 (1)
(1)
мұндағы
 - нүкте массасы,
- нүкте массасы,
 - оның үдеуі.
- оның үдеуі.
Материялық нүкте қозғалысының диференциалдық теңдеулері.
 ,
,
 ,
,
 (2)
(2)
мұндағы
 - нүкте үдеуінің осы координаттық өстердегі проекциялары,
- нүкте үдеуінің осы координаттық өстердегі проекциялары,
 - нүктеге әсер етуші күштің осы өстердегі проекциялары. (2) теңдеулері материялық
нүкте қозғалысының декарттық координаттар өстеріне қатысты алынған дифференциалдық теңдеулері
деп аталады.
- нүктеге әсер етуші күштің осы өстердегі проекциялары. (2) теңдеулері материялық
нүкте қозғалысының декарттық координаттар өстеріне қатысты алынған дифференциалдық теңдеулері
деп аталады.
Нүкте қозғалысы табиғи тәсілде берілген болса
 ,
,
 ,
,
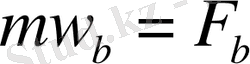
мұндағы
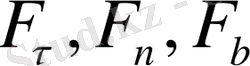 - нүктеге түсірілген
- нүктеге түсірілген
 күшінің табиги өстер бағыттарындағы проекциялары (жанама, бас нормаль, бинормаль),
күшінің табиги өстер бағыттарындағы проекциялары (жанама, бас нормаль, бинормаль),
 - үдеу векторының осы өстердегі проекциялары. Нүкте кинематикасында дәлелденген:
- үдеу векторының осы өстердегі проекциялары. Нүкте кинематикасында дәлелденген:
 ,
,
 ,
,

Бұдан
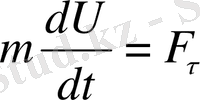 ,
,
 ,
,
 (3)
(3)
Нүкте қозғалысы полярлық координаттармен берілген болса
 ,
,
 (4)
(4)
Динамиканың бірінші және екінші есептері.
Нүкте динамикасында негізгі екі есеп бар. Оның бірішісінде материялық нүкте қозғалысының заңы және оның
 массасы беріледі. Осы заңдылықта болатын қозғалысты тудыратын күшті табу керек болады. Екінші мәселеде берілген күш бойынша массасы
массасы беріледі. Осы заңдылықта болатын қозғалысты тудыратын күшті табу керек болады. Екінші мәселеде берілген күш бойынша массасы
 -ге тең нүкте қоғалысының заңын анықтау керек.
-ге тең нүкте қоғалысының заңын анықтау керек.
Бірінші есепте нүкте массасы
 және оның қозғалысының кинематикалық теңдеулері
және оның қозғалысының кинематикалық теңдеулері
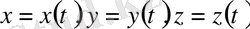 берілген болады. Осы берілгендер арқылы (2) теңдеулерінен іздеп отырған күштің проекциялары табылады:
берілген болады. Осы берілгендер арқылы (2) теңдеулерінен іздеп отырған күштің проекциялары табылады:
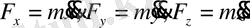 . Осы күш проециялары арқылы күштің өзін анықтай аламыз.
. Осы күш проециялары арқылы күштің өзін анықтай аламыз.
Нүкте динамикасының екінші есебін шешу екінші ретті үш дифференциалдық теңдеулер жүйесі (2) -ні интегралдауға келтіреді.
Берілген
 күш уақытқа, кеністіктегі нүктенің орналасуына және оның қозғалыс жылдамдығына тәуелді, яғни
күш уақытқа, кеністіктегі нүктенің орналасуына және оның қозғалыс жылдамдығына тәуелді, яғни
 , осыдан:
, осыдан:
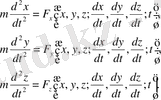 (5)
(5)
Берілген нүктенің қозғалыс заңын табу үшін (5) -ші теңдеулерді интегралдаймыз, мұнда белгісіз функциялар қозғалатын нүктенің координаттар болады, яғни (5) -нің жалпы шешімі (жалпы интегралдар)
 (6)
(6)
Мұнда нүкте координаттары уақытқа және алты кез келген тұрақты шамаларға тәуелді функциялар ретінде анықталған.
Сонымен, жалпы жағдайда нүкте координаттары алты кез келгентұрақты шамаларға тәуелді болып шықты.
Қозғалыс теңдеулерін интегралдау арқылы материялық нүктенің берілген күш әсерінен мүмкін болатын қозғалыстарының барлығының да заңдарын табуға болады. Егер нүктенің бастапқы орны мен жылдамдығын әртүрлі етіп алсақ, онда соған қарай берілген
 күшінің әсерінен біздің нүктеміз әртүрлі қозғалыс жасайтын болады.
күшінің әсерінен біздің нүктеміз әртүрлі қозғалыс жасайтын болады.
Сол себепті күштің өзгеру заңдылығын көрсетумен қатар, нүктенің бастапқы орны мен жылдамдығын да нақтылы көрсетіп отыруымыз қажет.
Уақыт
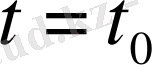 болғанда (
болғанда (
 - бастапқы уақыт), нүктенің бастапқы орның анықтайтын координаттар мынандай болады:
- бастапқы уақыт), нүктенің бастапқы орның анықтайтын координаттар мынандай болады:
 Ал бастапқы жылдамдық проекциялары:
Ал бастапқы жылдамдық проекциялары:
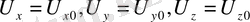 немесе
немесе
 .
.
Осы бастапқы шарттар арқылы интегралдау тұрақтылары табылады.
 (7)
(7)
Аңықталған интегралдау тұрақтыларының мәндерін (6) -ші теңдеуге қойсақ, мынаны аламыз:
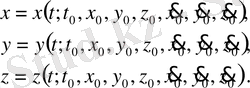 (8)
(8)
(8) -теңдіктер берілген күш әсерінен болатын және бастапқы шарттарға сәйкес орындалатын нүкте қозғалысының заңын анықтайды. Сонымен нүкте динамикасының екіші есебінің шешілуі осы сұба бойынша жүргізіледі.
Материялық нүкте динамикасының екінші есебін шешуде қоғалыстың диффренциалдық теңдеулерінің біріші интегралдарын табу өте маңызды орын алады. Егер өзара тәуелсіз алты бірінші интегралдар табылған болса:
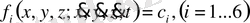 (9)
(9)
онда қозғлыстың дифференциалдық теңдеулерінің жалпы шешімін де мына түрде таба алар едік:
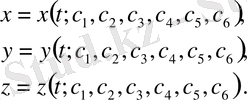 (10)
(10)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz