Икемділік коэффициенті

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

ОӨЖ

Икемділік коэффициенті

Орындаған: Қадырова Ж. Р.

Тобы: УА-303

Тексерген: Жаксыгулова Д. Д

Семей 2015 жыл

Жоспар

Кіріспе

Негізгі бөлім

Икемділік коэффициентінің мәні

Көптік регрессия теңдеуін құра отырып, икемділік коэффицентін мысал арқылы көрсету

Қорытынды

Пайдаланылған әдебиеттер тізімі

Икемділік коэффициентінің мәні

Егер экономикалық құбылыстар арасында сызықты емес қатыстар болса, онда оларды сызықты емес функциялар көмегімен өрнектеуге болады. Екі сызықты емес регрессия теңдеуінің класы бар;
Талдауға енгізілген айнымалыға қарағанда сызықты емес, бірақ бағаланатын параметрге сызықты болатын регрессия мысалы,

әртүрлі дәрежелі полиномдар -, ;
тең қабырғалы гипербола -;
жартылай логарифмдік функция -

Бағаланатын параметрге қарағанда сызықты емес регрессия, мысалы :

дәрежелі -;
көрсеткіштік -;
екінші ретті парбола теңдеуі, ол мынадай алмастыруларбойынша сызықты түрге келтіріледі.

Нәтижесінде, екі факторлы теңдеуге келтіреміз: 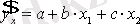$C:\Users\Zhanar\Desktop\3_clip_image017.gif$ . Параметрлерді бағалау ЕККӘ бойынша табылады :

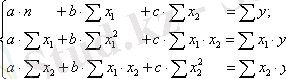
$C:\Users\Zhanar\Desktop\3_clip_image019.gif$

Кері алмастыру арқылы мынаны табамыз:

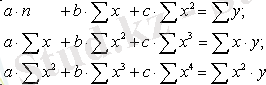
$C:\Users\Zhanar\Desktop\3_clip_image021.gif$

Тура байланыс кері байланысқа, немесе кері байланыстура байланысқа өзгереді. . Гиперболалық түрін сызықты түрге келтіру үшін мынадай алмастыру жасаймыз. приводится к линейному уравнению простой заменой $C:\Users\Zhanar\Desktop\3_clip_image023.gif$ . ЕККӘ қолданып, мынадай жүйе аламыз :

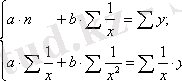
$C:\Users\Zhanar\Desktop\3_clip_image025.gif$

Осы тәртіппен 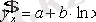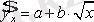$C:\Users\Zhanar\Desktop\3_clip_image026.gif$ , $C:\Users\Zhanar\Desktop\3_clip_image028.gif$ теңдеуінің түрлері де сызықты түрге келтіріледі. ие. Сызықты емес моделдерде дәрежелік функция жиі қолданылады, яғни 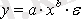$C:\Users\Zhanar\Desktop\3_clip_image030.gif$ , ол сызықты түру келтірілу үшін логарифмделеді:

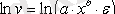
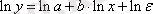
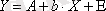
$C:\Users\Zhanar\Desktop\3_clip_image032.gif$ $C:\Users\Zhanar\Desktop\3_clip_image034.gif$ $C:\Users\Zhanar\Desktop\3_clip_image036.gif$

Мұндағы 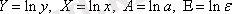$C:\Users\Zhanar\Desktop\3_clip_image038.gif$ . Яғни, ЕККӘ қолданылады және мынадай жүйе шығады:

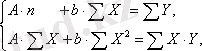
$C:\Users\Zhanar\Desktop\3_clip_image040.gif$

Содан кейін потенцирлейміз де ізделінді теңдеуді табамыз.
Дәрежелік функцияны кеңінен қолданатын себебіміз, b параметрі нақты экономикалық мәні болып табылады, яғни ол икемділік коэффициенті . Икемділік коэффициенті- егер фактор 1% ке өзгерсе онда нәтиже шамамен қаншаға өзгеретіндігін көрсететін коэффициент.

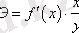$C:\Users\Zhanar\Desktop\3_clip_image044.gif$ .

Қалған функциялар үшін, икемділік коэффициенті тұрақты шамабола алмайды. Ол тек х фактрының мәндеріне байланысты болады. Сонда,

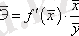$C:\Users\Zhanar\Desktop\3_clip_image046.gif$ .

Кесте №1. Икемділік коэффициентін есептеуге арналған формулалар

Функция түрі, y

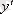
$C:\Users\Zhanar\Desktop\3_clip_image050.gif$

Икемділікиің орташа коэффициенті $C:\Users\Zhanar\Desktop\3_clip_image052.gif$

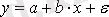
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image054.gif$

: b

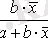
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image057.gif$

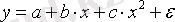
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image059.gif$

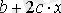
: $C:\Users\Zhanar\Desktop\3_clip_image061.gif$

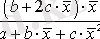
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image063.gif$

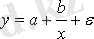
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image065.gif$

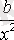
: $C:\Users\Zhanar\Desktop\3_clip_image067.gif$

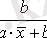
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image069.gif$

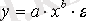
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image071.gif$

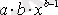
: $C:\Users\Zhanar\Desktop\3_clip_image073.gif$

Икемділікиің орташа коэффициенті: b

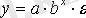
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image075.gif$

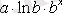
: $C:\Users\Zhanar\Desktop\3_clip_image077.gif$

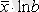
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image079.gif$

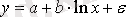
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image081.gif$

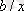
: $C:\Users\Zhanar\Desktop\3_clip_image083.gif$

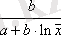
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image085.gif$

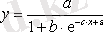
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image087.gif$

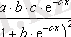
: $C:\Users\Zhanar\Desktop\3_clip_image089.gif$

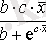
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image091.gif$

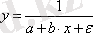
Функция түрі, y: $C:\Users\Zhanar\Desktop\3_clip_image093.gif$

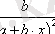
: $C:\Users\Zhanar\Desktop\3_clip_image095.gif$

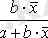
Икемділікиің орташа коэффициенті: $C:\Users\Zhanar\Desktop\3_clip_image097.gif$

Сызықты емес теңдеуде сызықты теңдеудегі сияқты байланыс тығыздығын есептеуге болады. Бұл жағадйжа корреляция индексі есептеледі:

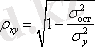
$C:\Users\Zhanar\Desktop\3_clip_image099.gif$

мұндағы 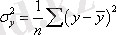$C:\Users\Zhanar\Desktop\3_clip_image101.gif$ - у шешуші белгінің жалпы дисперсиясы., 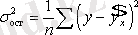$C:\Users\Zhanar\Desktop\3_clip_image104.gif$ - қалдық дисперсия 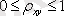$C:\Users\Zhanar\Desktop\3_clip_image106.gif$ . Егер нәтиже 1- ге жуықтаса, онда байланыс жақсы, теңдеу дұрыс құрылған деп есептеледі.
Детерминация коэффициентінің индексін есептейді:

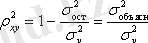
$C:\Users\Zhanar\Desktop\3_clip_image108.gif$

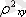$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ детерминация индексін детерминация коэффициентімен салыстырамыз: регрессия сызығының қисығы үлкен болса, онда соғұрлым 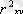$C:\Users\Zhanar\Desktop\3_clip_image112.gif$ шамасы 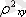$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ нан кіші . Бұл алынған функцияның күрделілігін білдіреді. Сондықтан сызықты регрессия теңдеуін алу қажет.
Детерминация индексі регрессия теңдеуін Фишер критерийі бойынша тексеру үшін қолданылады.

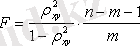
$C:\Users\Zhanar\Desktop\3_clip_image115.gif$

Мұндағы 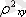$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ - детерминации индексі, n - бақылау саны, m - х айнымалысы бойынша параметр саны, F - критерийінің нақты мәні кестелік мәнімен салыстырылады, егер α және еркін түсу көрсеткіші саны 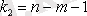$C:\Users\Zhanar\Desktop\3_clip_image125.gif$ қалдық квадраттар қосындысы үшін) және 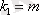$C:\Users\Zhanar\Desktop\3_clip_image127.gif$ (факторлық квадратының қосындысы үшін ) .

Көптік регрессия теңдеуін құра отырып, икемділік коэффицентін мысал арқылы көрсету

Егер фактордың айнымалыға тәуелділігін сызықтық теңдеу түрінде сипаттау мүмкін болмаса, онда сызықтық емес функция көмегімен сипаттауға болады. Сызықтық емес регрессияның парметрлерін қосылған параметрлері бойынша бағалау, сызықтық регрессия сияқты ең кіші квадраттар әдісі (ЕКӘ) арқылы анықталады, яғни бұл функциялар параметрлер бойынша сызықты. Кез келген полиномды көптік регрессияның сызықтық моделіне келтіруге болады. Соның ішінде икемділік коффициентін қолдану арқылы берілген мысалды қарастырайық.

Мақсаты: Икемділік коэффициентін қолдана отырып, Көптік регрессия теңдеуін құру, оның парметрлерін бағалау.

МЫСАЛ: (есептеулердің көлемін шектеу үшін, 10 бақылауды қарастырамыз) . сипаттайтын процесс Бір жұмысшының көмірді өндіруі y (т), пластың қуаттылығы (м) , және жұмыс механизациясының деңгейі (%) тәуелділігі көрсетілген.

Кесте №1

№

№: Х ₁

1: 8

2: 11

3: 12

4: 9

5: 8

6: 8

7: 9

8: 9

9: 8

10: 12

№: Х ₂

1: 5

2: 8

3: 8

4: 5

5: 7

6: 8

7: 6

8: 4

9: 5

10: 7

№: У

1: 5

2: 10

3: 10

4: 7

5: 5

6: 6

7: 6

8: 5

9: 6

10: 8

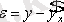
У, Х _1, Х ₂ айнымалылары арасында сызықты корреляциялық байланыс бар деп есептеп линейная Х ₁ және Х ₂ бойынша у регрессия теңдеуін табамыз. Мынадай кесте құрамыз: $C:\Users\Zhanar\Desktop\pr3_clip_image014.gif$