Дискреттік модельдеу

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Қазақстан Республикасы Білім және Ғылым Министрлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

Автоматика және электротехника кафедрасы

СӨЖ

Тақырыбы: Дискреттік модельдеу

Орындаған: Жапар Ботагөз

Тобы: ВТ-305

Қабылдаған: Қожахметова Д. О

Семей 2015 ж

Мазмұны:

1. Модельдеу ұғымы . . . 3

2. Модельдеу түрлері . . . 4

Пайдаланған әдебиеттер тізімі . . . 7

1. Модельдеу ұғымы. Модельдеу (моделирование; simulation) - кез-келген құбылыстардың, процестердің немесе объект жүйелерінің қасиеттері мен сипаттамаларын зерттеу үшін олардың үлгісін құру (жасау) және талдау; бар немесе жаңадан құрастырылған объектілердің сипатын анықтау немесе айқындау үшін олардың аналоктарында (модельде) объектілердің әр-түрлі табиғатың зеттеу әдісі. Модель төрт денгейде түпнұсқанын гноселогиялық орынбасары бола алады: 1 - элеметтер денгейінде, 2 - құрлым деңгейіде, 3 - қалып - күй немесе қызметік деңгейін, 4 - нәтижелер деңгейінде. Сипаты бойынша модельдеу объектінің геометриялық, физикалық, динамикалық және қызметтік сипатын нақты дәл береді. Идеалдық моделдеуге объектінің ойдағы бейнесі жатады. Ойша модельдеу тіл көмегімен іске асырылады. Компьютерлік модельдеу - бұл да оқып үйренетін объекті теориясының модельденуі. Өндірістік және экономикалық процестерді модельдеу - процестерді процестер құрылымын кескіндейтін, ақпараттар ағыны мен объектілерді сипаттайтын модель құру жолымен зерттеу. Модельді уақыт факторына байланысты динамикалық және статистпикалық деп екі топқа жіктеуге болады.

Модельдеу - әлемді тану мен өзгертудің әдістерінің бірі. Ол сол әдістердің жаңа қызметтерін ашатын (микро-, макро-, мега әлемнің процестері мен құбылыстары, кибернетикалық және имитациялық модельдерді жасау, жүйелік техниканың тууы т. б. ) модельдердің жаңа типтерін жасауға негіз болған ғылымның дамуымен байланысты кең тарады.

модельдер құрудың және оларды сәйкес құбылыстар, процестер, объектілер жүйесі негізінде оқып білу әдістерінің жиыны;
зерттеу объектілерінің сипаттамаларын біліп алу немесе анықтап алу үшін, басқаруды жақсарту немесе нұсқа жөнінде сәйкес болжамды тексеру үшін, жаңадан құрастырылатын объектілерді жасау тәсілдерін тиімді ету үшін модельдерді зерттеу нәтижесін пайдалану әдістерінің жиыны. Модель, нұсқаны табиғи жағдайларда зерттеу кандай да болсын себептермен қиын немесе мүмкін болмағанда, кандай да бір объектіні зерттеу процесін жеңілдету керек болғанда қолданылады. Әдістер модельдің сипатына, оны қолдану алаңы мен зерттеу мақсатына тәуелді;
өзінің қүрделілігі мен өлшемдері бойынша сол күйінде зерттеуге мүмкіндік бермейтін қандай да болсын объектілерді қайталап жасау. Модельдеуғылым, техника, технология негіздері бойынша қабілеттерді дамытуға көмектеседі.

2. Дискреттік модельдеу - оқиғалардың үзіліссіз табиғатынан абстракциялануды жəне модельденетін жүйелердің негізгі оқиғаларын ғана қарастыруды ұсынатын модельдеу тəсілдемесі. Дискреттік-оқиғалық модельдеу неғұрлым дамыған жəне жаппай қызмет көрсететін логистикалар мен жүйелерден көлік жəне өндірістік жүйелерге дейін - қосымшалардың аса үлкен аясына ие. Модельдеудің осы моделі өндірістік үдерістерді модельдеу үшін көбірек дəл келеді. Оны Джеффери Гордон 1960 жылдары негіздеген болатын.

Дискреттік программалау модельдері

Бульдік айнымалыларды пайдаланып шығарылатын тəжірибеде жиі кездесетін маңызды есептердің бірі дискретті программалау есептері. Олар, есептеу объектісі жəне факторлары физи-калық түрде бөлінбейтін есептер. Ізделініп отырған айнымалылары тек бүтін мəндер қабылдайтын (мысалға, штаттық расписанияны жоспарлау жəне мəндері нөль немесе бір болатын логикалды немесе бульдік айнымалы жұмысқа тағайындау есептері) есептерді жатқызады. Сонымен, мұндай есептердің ерекшеліктері жəне екілік айнымалы есептерден айрықшылықтары былай түсіндіріледі: оңтайластырудың нəтижесінде оңтайлы мəндері ізделініп отырған айнымалылардың өзгеру аралығында кез келген үздіксіз мəндерінің бірі емес, тек олардың берілген нақты мəндерінің ішіндегі біреуі оңтайлы болуы мүмкін. Сондықтан мұндай сандар бүтін немесе бөлшек сандарда болады. Дискретті программалау есептеріне бір мысал қарастырайық.

Мысал. Формасы параллелипипед болып келетін бактың сиымдылығы максимальды болатындай, табанының ені (a) жəне ұзындығы (b), сонымен қатар биіктігінің (h) ұзындықтарын табу керек. Бак жасауға, ені: a = 4, 25; 5, 5 жəне 6, 75 м, материалдарды қолдану ұсынылды. Материалдардың бағасы: С = kS =100 мың теңге, мұндағы k - 1 м2 материалдың бағасы k =10 мың теңге, S - бак жасауға кеткен материал, м2. Есептің математикалық моделін құрамыз. Бактың көлемі:

V = abh, м3.

Бак жасауға керекті материалдың ауданы:

S = 2 (ab) + 2 (a +b) h = 2 (ab + (a + b) h), осыдан аламыз

С = kS =2 k(ab + (a + b) h) .

Осындай əрекеттерден кейін есептің оңтайластыру моделін құрамыз:

V = abh → max

Берілген материалдардан жасалған максимальды сиымды бактың құны берілген бағадан (Сбер) көп болмауға тиіс:

2k (ab + (a + b) h) ≤ Сбер, a, b, h ≥ 0 жəне a ∈ 4. 25; 5. 5; 6. 75.

Есептің шарты бойынша бактың бағасы Сбер =100 жəне k =10 мың теңге екенін ескерсек, онда бірінші теңсіздікті былай жазуға болады:

2·10 (ab + (a + b) h) ≤ 100 немесе ab + (a + b) ≤ 5 (a)

Осыдан кейін бульдік айнымалылар арқылы математикалық модель мына түрде жазылады:

a = 4, 25δ1 + 5, 5 δ2 + 6, 75 δ3 немесе

a - 4, 25δ1 - 5, 5 δ2 - 6, 75 δ3 = 0 (б)

δ1 + δ2 + δ3 =1 (в)

0 ≤ δj ≤ 1, j = 1, 2, 3.

δj - бүтін, j = 1, 2, 3.

Сонымен сызықты емес оңтайластыру моделі құрылды. Есепті MS Excel-де шығарамыз. Жұмыс бетіне барлық деректерді жазып, кестелік модель тұрғызамыз. Ол үшін B2:G2 аралықта мəндері ізделініп отырған (бульдіктермен қоса) айнымалылардың белгілері, E4:G4; E5:G5 жəне E6:G6 аралықтарда бульдік айнымалылардың төменгі жəне жоғары мəндері, сонымен қоса олардың бүтін сандар болу шарттары жазылды (1-сурет) .

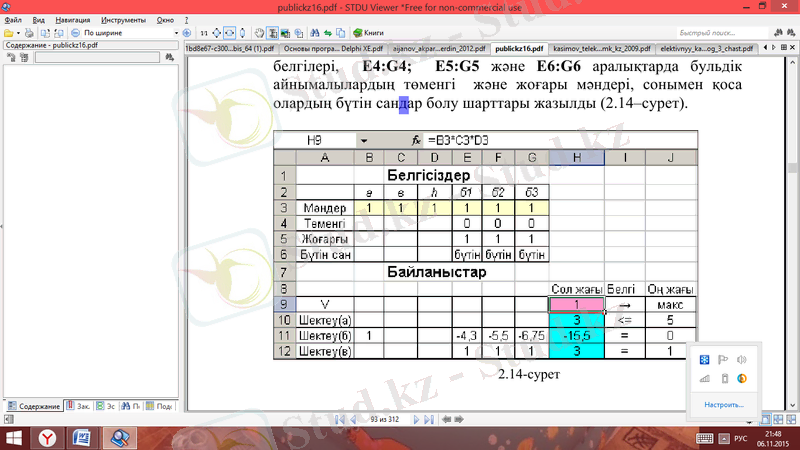
Жоғарыда сызықты емес программалау есебінің математикалық моделі құрылғаны аталды. MS Excel көмегімен сызықты емес программалау есебін шығару тəсілінде сызықты программалау есебіне қарағанда мынадай өзгешеліктер бар:

- барлық ізделінетін айнымалыларға бастапқы мəндер тағайындалынады;

- Поиск решения-ның Параметры-де Линейная модель-ді іске қосудың қажеті жоқ.

Бірінші талапты қамтамасыздандыру мақсатында B3:G3 аралыққа 1 жазамыз (1-сурет) . H9 ұяға мақсат функция формуласы: =B3*C3*D3, сонымен қатар H10, H11 жəне H12 ұяларында, сəйкесінше (а), (б) жəне (в) шектеулер формулаларының сол жағы: =B3*C3+(B3+C3) ;

=СУММПРОИЗВ (E11:G11; $E$3:$G$3) +B3 жəне

=СУММПРОИЗВ(E12:G12; $E$3:$G$3) жазылады.

Поиск решения құралында мақсат функция ұясының адресін жəне бағытын, айнымалылар ұяларының аралығын жəне шектеулерді енгізгеннен кейінгі сұхбаттасу терезесінің бейнесі 2-суреттегідей болады.

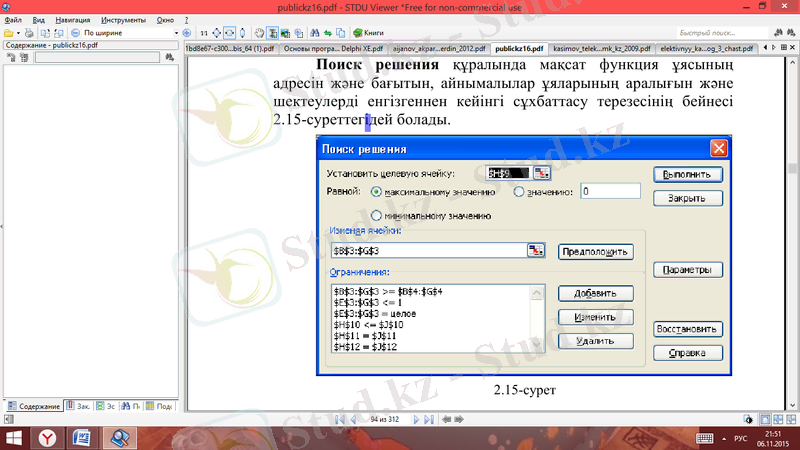
2-сурет

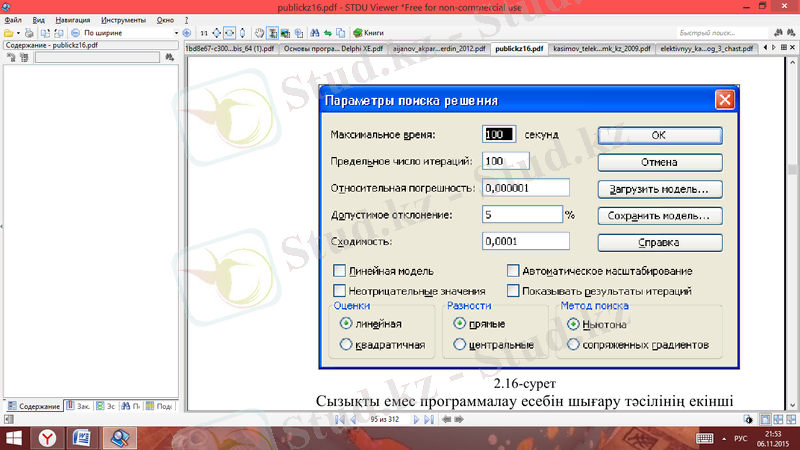
3-сурет

Сызықты емес программалау есебін шығару тəсілінің екінші талабы бойынша Парамер-дің сұхбаттасу терезесі 3-суреттегідей қалыпта қалады. Выпонить батырмасын басқаннан кейін есептің шешімін аламыз (4-сурет) .

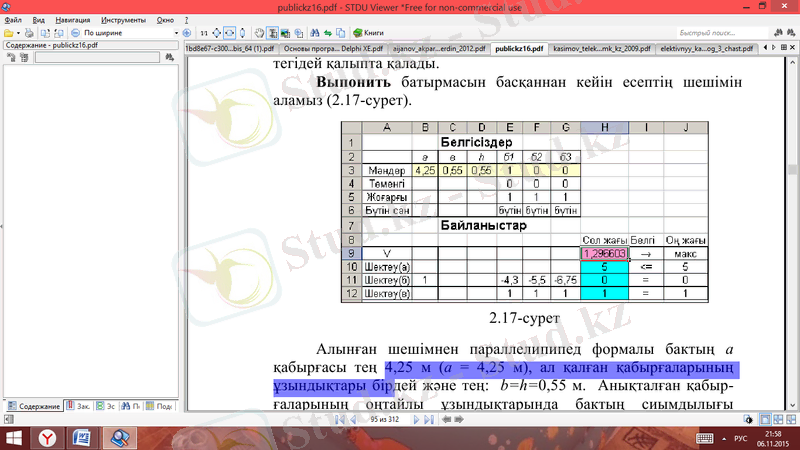
4-сурет

Алынған шешімнен параллелипипед формалы бактың а қабырғасы тең 4, 25 м (a = 4, 25 м), ал қалған қабырғаларының ұзындықтары бірдей жəне тең: b=h=0, 55 м. Анықталған қабырғаларының оңтайлы ұзындықтарында бактың сиымдылығы максимальды жəне тең: V= 1, 2966 м3 . Бактың а қабырғасының ұзындығы (4, 25, 5, 5 жəне 6, 75 м) берілген жəне математикалық модельде олар туралы қосымша шектеулер қарастырылғандықтан, табылған бактың сиымдылығы, есепті қосымша шектеусіз шығарған сиымдықтан азаяды. Сонымен, дискреттік программалау көмегімен алдын ала берілген мəндердің ішінен экстремальдық мəнге жетуге ықпал жасайтындай бір мəнді алуға болады, бірақ мұндай əдістен мақсат функция жақсармайды. Дискретті программалау есептерін шығару барысында тек нəтиже бойынша есеп (Отчет по результатам) алынады. Онда ешқандай да жаңа деректер болмайды, сондықтан оны талдау қажетсіз. Нұсқалық талдау қалай жүргізілетініне тоқталсақ, олда сызықты емес программалау есептерінде қолданылған тəсілдер арқылы жүргізілетінін байқаймыз. Дискреттік программалау есептерін шығарғанда параметрлік талдау біраз қызықты. Мысалға, 4-суретте қарастырылып отырған есептің ізделіп отырған пара-метрлері (бактың қабырғаларының ұзындығы) үздіксіз (есепті бульдік айнымалыларысыз шешу) жəне үздікті (яғни дискретті программалау есебі құрылып, бірнеше мəндердің ішінен бір мəнді, бульдік айнымалылары арқылы таңдау) болған жағдайда нəтижелерді салыстырыу үшін сценария кестесі келтірілген.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.