Жобалау процесіндегі жүктеулердің нормативтік және есептеу мәндері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ ШӘКӘРІМ АТЫНДАҒЫ СЕМЕЙ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
«Геодезия және құрылыс » кафедрасы
СӨЖ
Тақырыбы: «Жобалау барысындағы жүктеулердің нормативтік және есептеу мағыналары. »
Орындаған: Кенесов Е
Тобы: СТ-309с
Тексерген: Оқасов А. Р
Семей-2015
Жоспар
Кіріспе
1. Негізгі бөлім:
1. 1 Бір арматурасы бар тік төртбұрышты және таврлы қималы элементтердің нормальді қимасы бойынша беріктігіне есептеу.
1. 2 Иілетін элементтердің көлбеу қимасы бойынша көлденең күшке есептеу. 1. 3 Көлденең сырықтарды есептеу
Қортынды
Пайдаланылған әдебиеттер тізімі.
Кіріспе
Кез келген симметриялы формалы элементті беріктікке нормальді қима бойынша есептегенде, элементтің шектік жағдайда тепе-теңдікте тұрғанын қабылдайды ΣМ=0 және ΣХ=0 .
Элементтің көтеру күші бірдей болған жағдайда, арматура қимасы соғұрлым кіші болады, егер h o жұмысшы қиманың биіктігі ұлғайса. Яғни арматурасы көп және аз қималарды алуға болады.
Төртбұрышты элементке қарағанда таврлы элемент тиімді болып саналады, өйткені көтеру қабілеті бірдей болғанымен бетон шығыны аз болады. Полкалардың ені үлкен болған жағдайда қабырғадан ең үлкен аралықта жатқан свесте кернеу аз болады.
Жобалау барысындағы жүктеулердің нормативтік және есептеу мағыналары.
Кез келген симметриялы формалы элементті беріктікке нормальді қима бойынша есептегенде, элементтің шектік жағдайда тепе-теңдікте тұрғанын қабылдайды ΣМ=0 және ΣХ=0.
Кернелмейтін бір арматурамен армирлеген кезде ΣХ=0 теңдігін келесі түрде жазуға болады:
R b A bc = R s A s (1. 15)
Ал ΣМ=0 теңдігін келесі түрде жазуға болады:
М ≤ М u = R b A bc z b = R b S b c(1. 16)
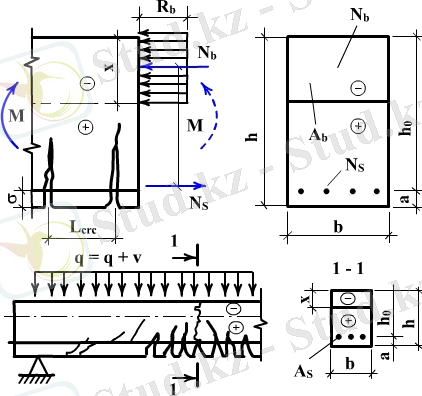
Сурет 7, 1. Иілген элементті есептеуде
а- кернеу мен күштің сұлбасы; б- бұзылу сұлбасы.
А b = bx; z b = h o - 0, 5x; S b = А b z b = bx(h o - 0, 5x)
R b bx = R s A s ; x = R s A s /(R b b) (1. 17)
ξ = x/h o = R s A s /(R b bh o ) ; M ≤ R b bx(h o - 0, 5x) (1. 18)
Мұндағы,
ξ - қысылатын аймақтың салыстырмалы биіктігі.
Сонымен қатар, қысылатын аймақтың ауырлық центрімен өтетін өс арқылы момент көмегімен өрнектеуге болады:
M ≤ R s A s (h o - 0, 5x) (1. 19)
(1. 17), (1. 18), (1. 19) формулаларын бірге қолданады. Олар келеді егер x<ξ R h o , мұндағы ξ R - қысылатын аймақтың шектік салыстырмалы биіктігі, бұл кезде арматурадағы созу кернеуі шектік мәнге ие болады σ s →R s .
ξ R = x R /h o = ω/{1 + σ s R/σ scu (1 - ω/1, 1) } (1. 20)
Элементтің көтеру күші бірдей болған жағдайда, арматура қимасы соғұрлым кіші болады, егер h o жұмысшы қиманың биіктігі ұлғайса. Яғни арматурасы көп және аз қималарды алуға болады.
Армирлеу коэффициенті
μ = A s /(bh o ) (1. 21)
Және армирлеу үлесі μ 100, келесі қатынастарды ескергенде bxR b = R s A s және ξ=x/h o келесі түрде көрсетілуі мүмкін:
μ = ξR b /R s ; 100μ = 100ξR b /R s (1. 22)
Осы жерде төртбұрышты қимадағы арматура үлесінің максималды мәнін табуға болады ξ R .
Таврлы қималар көп жағдайда жеке элемент немесе құрастырмалы, монолитті конструкциялар құрамында кездестіруге болады. Таврлы қималы элемент полка және қабырғадан тұрады, көбінесе бір арматуралы болып келеді(сурет 7, 2) .
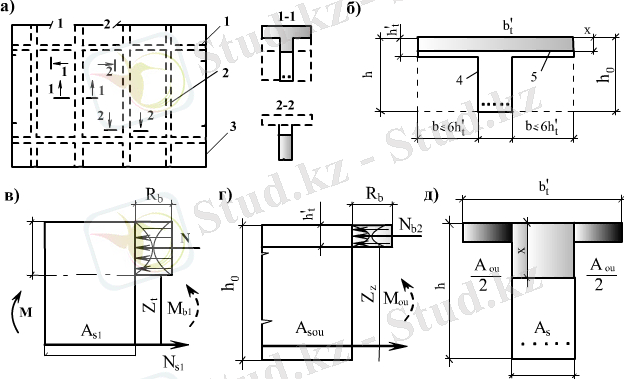
Сурет 7, 2. Таврлы қима.
Төртбұрышты элементке қарағанда таврлы элемент тиімді болып саналады, өйткені көтеру қабілеті бірдей болғанымен бетон шығыны аз болады. Полкалардың ені үлкен болған жағдайда қабырғадан ең үлкен аралықта жатқан свесте кернеу аз болады. Сондықтан, есептерде полкалар свесінің эквивалентті енін b' f кіргізеді, нормалар қажет еткенде мәнін шектеп отырады.
Егер қысылған аймақтың астыңғы шегі полка аралығында жатса (сурет 7, 2 б), онда таврлы қиманы тік төртбұрышты сияқты есептейді, өлшемдері b' f және h 0 , өйткені созылған аймақтың бетоны көтеру қабілетіне әсер етпейді.
Есептік формулалар (кернелмеген элементтер үшін) :
Егер қысылған аймақтың астыңғы шегі полкадан төмен орналасса, онда қиманың қысылған аймағы қабырғаның қысылған аймағынан және полка свесінен тұрады.
Қысылған аймақтың астыңғы шегі келесі теңдеумен анықталады
Созылған арматурадағы біркелкі әсер ететін күштер арқылы өтетін нүкте бойымен момент бойынша беріктік шарты:
Таврлы қима үшін келесі шарт орындалуы тиісx≤ξ R h o .
2 Иілетін элементтердегі көлбеу қималарының түзілуі ию моменті мен көлденең күш әсерінен болады.
Элементтің көлбеу қимасы бойынша көлденең күшіне қарсы беріктігі:
Q ≤ Q sw +Q s, ins + Q b ; (1. 27)
Q sw = ΣR sw A sw немесе Q sw =q sw c o (1. 28)
q sw = R sw A sw /s (1. 29)
c o =√{φ b2 (1+φ t +φ n ) R bt bh 2 o }/q sw =√M b /q sw (1. 30)
Q s, ins = ΣR sw A s, ins sinθ (1. 31)
Q b =M b /c=φ b2 (1+φ f +φ n ) R bt bh 2 o /c (1. 32)
Мұндағы,
Q sw - көлбеу сызаттарымен өтетін, бір көлденең арматураның қабылдайтын көлденең ішкі күш (сурет 7, 3) ;
Q s, ins - көлбеу сызаттарымен өтетін, отгибтардың қабылдайтын көлденең ішкі күш;
Q b - армирленген көлбеу қимадағы қысылған бетонның қабылдайтын көлденең ішкі күш;
q sw - көлбеу қима аралығында элемент ұзындығы бірлігіндегі қамыттардағы күш;
c o - қамыттардың жұмысы ескерілетін элемент ұзындығы, немесе элементтің бойлық өсіне қауіпті көлбеуінің проекциясы;
θ - элементтің бойлық өсіне отгибтардың иілу бұрышы;
φ b2 - бетон түрін ескеретін коэффициент.
Көлбеу қималарын көлденең күштерге есептеудегі басты мақсат - бетон қимасының және бойлық арматураның жеткілікті екенін есептеу, керекті ауданды және қамыттардың дұрыс орналасуын қадағалауболып табылады.
Есептеу кезінде сонымен қатар, қамыттар s , аралығындағы, тірек пен отгиб арасындағы s 1 , және отгиб араларындағы s 2 беріктігін қамтамасыз ету қажет (сурет 7, 3 а) .
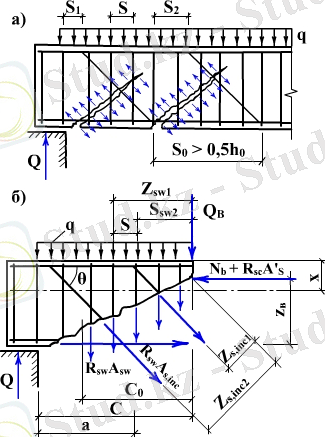
Сурет 3, 7. Көлбеу қималарын есептеуде
3 Көп кезде алдын ала кернелген отгибсіз таврлы қималар кездеседі.
Есептеуді келтірілген формулалар арқылы жүргізеді, бұл кезде көтеру қабілеті ең төмен қималарды есептейді (сурет 3, 8) .
Берілгендер белгілі болғанда, есепті келесі қатармен есептейді:
1. Бірінші жағдай бойынша көлденең арматура керек пе жоқ па екенін тексереді.
2. Екінші жағдай бойынша көлденең арматура керек пе жоқ па екенін тексереді.
Егер керек болса - есепті жалғастырады.
3. Q bmin мәнін анықтайды (1. 32), формула бойынша.
4. q sw мәнін (1. 29) формула бойынша есептейді, және келесі шарт q sw ≥Q bmin /2h ol бойынша тексереді.
5. s≤s max шарт бойынша қамыт қадамдарын табады, s max =φ b2 R bt bh 2 o /Q
6. М b мәнінформула (1. 30) бойынша есептейді.
7. с мәнінформула (1. 30) бойынша есептейдіжәнес≤(φ b2 /φ b3 ) h o .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz