Кванттық күй, асқын өткізгіштік, асқын аққыштық, фонодар, кристалдық торлар

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министірлігі

Семей қаласындағы Шәкәрім атындағы Мемлекеттік университеті

СӨОЖ

Пән: Конденсацияланған күй физикасы

Тақырыбы: Кванттық күй, асқын өткізгіштік, асқын аққыштық, фонодар, кристалдық торлар.

Орындаған : Қабдылқақов Ержан

Топ: ТФ-319

Тексерген: Сейсенбаева М. Қ

Семей 2015

Жоспар

1 Паули принціпі2

2 Фонондар3

3 Металдар және диэлектриктер4

4 Асқын өткізгіштік және асқын аққыштық5

1 Паули принціпі

Бор теориясы «рұқсат» етілген стационар орбиталардың радиустарын есептеп табуға мүмкіндік береді. (4) өрнекке сәйкес тек дискретті мәндер қабылдайды. Бұлар арқылы белгіленген. Сутегі атомындағы электронның ең кіші радиусын табу үшін (4) формулаға мәндерін қоямыз сонда 0, 0529нм шығады. Бұл Бор радиусы деп аталады. Бұл мән газдардың кинетикалық теориясынан алынған деректермен жақсы үйлеседі. Сонымен Бор теориясы атомдардың мөлшері үшін дұрыс мәндер береді.

Енді сутегі атомының мүмкін энергетикалық деңгейлерін анықтайық. Электрон ядродан шексіз қашықтықта болғанда оның потенциалдық энергиясын нөл деп аламыз. Осы жағдайда заряды +Ζе ядродан қашықтықтағы электронның 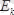кинетикалық және 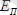потенциалдық энергияларын жеке есептеп табуға болады:

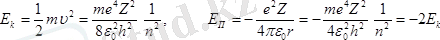Ал электронның толық энергиясы мынаған тең.

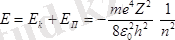
Бұдан электрон энергиясы кванттық санына тәуелді екенін көруге болады, ал =1, 2, 3, . . . мәндерін қабылдайды. Демек атомның дискретті энергия мәндері бар кұйлері ғана болуы мүмкін. Мұндағы минус таңбасы жүйенің байланысқа не екенін көрсетеді. Сонымен атом энергиясы квантталған деген қорытынды жасауға болады.

Атом ішіндегі электронның күйін сипаттау үшін n , l , m _s , m _l кванттық сандарын қолдануға болады. бас кванттық сан ( n ) энергия деңгейлерін анықтайды. Қосымша кванттық сан ( l ) электронның орбиталық қозғалыс мөлшері моментін сипаттайды; магниттік кванттық сан ( m _l ) болса, орбиталық қозғалыс мөлшері моментінің магнит өрісі бағытына түсірілген проекциясын сипаттайды; ал спиндік магниттік кванттық сан ( m _s ) электронның меншікті қозғалыс мөлшері моментінің өріс бағытына түсірілген проекциясын анықтайды.

Паулидың зерттеуінше бір атомның ішінде осы n , l , m _s , m _l кванттық сандарының мәндері бірдей екі электрон болуы мүмкін емес. Басқаша айтқанда, бір атомның ішінде екі электрон бір мезгілдебірдей күйде бола алмайды. Бұл Паули принципі (1925 ж) .

Егер электрондардың n , l , m _l кванттық сандары бірдей болса, онда Паули принципі бойынша олардың m _s кванттық саны бірдей болмауы тиіс, ал бұл кванттық санның мәне екі түрлі: m _s =+1/2 және : m _s =-1/2. Демек атомның ішінде n , l , m _l кванттық сандары бірдей екі электрон бола алады. Енді электрондардың n , l кванттық сандары ғана бірдей болсын, онда мұндай электрондардың m _l кванттық сандары бірдей болмауы тиіс. Ал l кванттық санның берілген бір мәніне сәйкес келетін m _l кванттық санның (2 l +1) мәндері болады; n , l , m _l кванттық сандарының әрбір мәніне m _s кванттық санының екі түрлі мәні сәйкес келеді. Сонда атомның ішінде n және l кванттық сандары бірдей көп дегенде 2(2 l +1) электрон бола алады. Енді атомның ішінде бас кванттық саны бірдей қанша электрон болуы мүмкін, соған тоқталайық. Бас кванттық санның берілген бір n мәніне сай l кванттық санның мәндері 0, 1, 2, . . . ( п -1) болатыны мәлім. Сондықтан бас кванттық сандары бірдей электрондардың ең көп мүмкін саны ( Z _n ) мына қосындымен өрнектеледі:

Бас кванттық саны бірдей электрондар тобы белгілі электрондық қабаттар немесе электрондық қабықтар түзеді. Олар K, L, M, N O, P, Q . . . әріптерімен белгіленеді, сонда бас кванттық саны п =1 электрондар K-қабатын; бас кванттық сан п =2 электрондар L-қабатын; бас кванттық саны п =3 электрондар M-қабатын; бас кванттық саны п =4 электрондар N-қабатын; бас кванттық саны п =5 электрондар O-қабатын; бас кванттық саны п =6 электрондар P-қабатын түзеді. Сонда K, L, M, N O . . . қабаттарында ретімен алғанда (12) формулаға лайық ең көбі, 2, 8, 18, 32, 50 электрон болады. Әрбір қабаттағы қосымша кванттық саны бірдей электрондар электрондық қабатшалар түзеді. Сөйтіп әрбір электрондық қабат бірнеше қабатшаларға бөлінеді, қосымша кванттық сан l =0, 1, 2, 3, болса, олар s , p , d , f , g , …әріптерімен белгіленеді. Әрбір қабатшада ең көп болғанда 2(2 l +1) электрон болады; сонда s- қабатшада ең көбі2 электрон, p - қабатшада ең көбі6 электрон, d- қабатшада ең көбі10 электрон, f- қабатшада ең көбі14 электрон бола алады.

2 Фонондар

Заттың қасиеттерінің корпускулалық-толқындық екіжақтылығына сәйкес, кристалдағы серпімді толқындармен энергиясы болатын фонондар қатар қарастырылады. Фонон дыбыс толқындары энергиясының кванты (өйткені серпімді толқындар - дыбыс толқындары) . Фонондар квазибөлшектер - өздерін микробөлшектер сияқты ұстайтын элементар қозулар болып табылады. Электромагниттік сәуленің квантталуы фотон туралы ұғым туғызғаны сияқты серпімді толқындардың квантталуы фонон туралы ұғымның тууына әкелді.

Квазибөлшектердің, оның ішінде фонондардың, кәдімгі бөлшектерден (мысалы, элеткрондар, протондар, фотондар) айырмашылығы көп, себебі олар жүйенің көптеген бөлшектерінің ұжымдық қозғалыстарымен байланысқан. Квазибөлшектер вакуумда болмайды, олар тек кристалдарда ғана өмір сүреді. Кристалда фонондардың соқтығысуы кезінде олардың импульсі кристалдық торға дискретт порция түрінде беріле алады - яғни ол сақталмайды. Сондықтан фонон жағдайында квазиимпульс ұғымы қолданылады.

Кристалдық тор энергиясы фонондық газ энергиясы түрінде қарастырылады. Ол Бозе-Эйнштейн статистикасына бағынады, сондықтан фонондар бозондар (олардың спиндері нөлге тең) болып табылады. Фонондар шығарыла және жұтыла алады, бірақ олардың саны тұрақты сақталмайды. .

3 Металдар және диэлектриктер

Металдардың электр өткізгіштігінің кванттық теориясының кванттық механикаға және Ферми-Дирактың кванттық статистикасына негізделеді. мұндағы: - металдағы электрондардың концентрациясы, - Ферми энергиясына ие электронның еркін жүру жолының орташа ұзындығы, осы электронның жылулық қозғалысының орташа жылдамдығы.

Кванттық теория электрондардың қозғалысын олардың кристалдық торымен өзара әсерін ескере отырып қарастырады. Корпускулалық- толқындық екіжақтылыққа сәйкес электронның қозғалысы толқындық процеспен қатар қойылады. Идеал кристалдық тор (оның түйіндерінде қозғалмайтын бөлшектер орналасады және онда периодтылықтың бұзылуы болмайды) оптикалық біртекті орта сияқты көрінеді - ол «электрондық толқындар» шашыратпайды. Бұл металдың электр тогына ешқандай кедергі болмайтындығын көрсетеді. «Электрондық толқындар» идеал кристалдық торда тарала отырып, тор түйіндерін орағытып өтіп, айтарлықтай біраз қашықтыққа орын ауыстырады.

Нақты кристалдық торда «электрондық толқындардың» шашырауы болады, бұл металдардың электрлік кедергілердің себебі болып табылады.

Қатты денелердің зоналық теориясы металдардың, диэлектриктерді және жартылай өткізгіштердің бар екендігіне олардың электрлік қасиеттерінің әртүрлілігін түсіндіре отырып, біржақты көзқарас тудырды. Осы заттардың электрлік қасиеттерінің әртүрлі екендігі біріншіден, рұқсат етілген зоналардың электрондармен толтырылуы бірдей еместігімен, екіншіден, тыйым салынған зонаның енімен түсіндіріледі.

Зонадағы энергетикалық деңгейлердің электрондармен толтырылу дәрежесі сәйкес атомдың деңгейлердің толтырылуымен анықталады. Егер осы кезде қандай да бір энергетикалық деңгей толық толтырылса, онда пайда болатын энергетикалық зона да тұтастай толтырылған болады. Жалпы жағдайда электрондармен толық толтырылған және еркін атомдардың ішкі электрондарының энергетикалық деңгейлерінен түзілген валенттік зона туралы, сонымен біррге не электрондармен жартылай толтырылған, не бос және оқшауланған атомдардың «ұжымдастырылған» ішкі элеткрондарының энергетикалық деңгейлерінен түзілген өткізгіштік зона (бос зона) туралы айтуға болады.

4 Асқын өткізгіштік және асқын аққыштық

Зоналардың электрондармен толтырылу дәрежесіне және тыйым салынған зонаның еніне байланысты төрт жағдай мүмкін болады.

Асқын өткізгіштердің қасиеттерін зерттеу мақсатында қойылған әр түрлі тәжірибелер металдың асқын өткізгіштік күйге өтуі кезінде оның кристалдық торының құрылымы өзгермейтіндігі, оның механикалық және оптикалық (көрінетін және инфрақызыл аумақтарда) қасиеттері өзгермейтіндігі туралы қорытындыға келді. Бірақ осындай өту кезінде электрлік қасиеттерінің секірмелі түрде өзгеруімен оның магниттік және жылулық қасиеттері де сапалық түрде өзгереді.

Неміс ғалымы В. Мейсснер көрсеткендей асқын өткізгіштік күйде асқын өткізгіште магнит өрісі болмайды. Бұл асқын өткізгішті критикалық температурадан төмен температураға салқындатқанда одан магнит өрісінің шығып кететіндігін көрсетеді (Мейсснер эффектісі) .

Асқын өткізгіштіктің физикалық табиғаты 1957 жылы ғана гелийдің асқын аққыштық теориясы (1941 ж. Ландау енгізді) негізінде түсінікті болды. Асқын өткізгіштік теориясын америка физиктері Д. Бардин, Л. Купер, Д. Шриффер (БКШ теориясы) енгізіп, Н. Н. Боголюбов дамытты.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.