Буындар түрлері және сипаттамалары

Пән: Автоматтандыру, Техника
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Қазақстан Республикасының Білім және ғылым министрлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

“Автоматтандыру және электротехника” кафедрасы

СӨЖ

Тақырыбы: Буындар түрлері және сипаттамалары.

Орындаған: Сиязбек Д. С

Тобы: АУ-301

Тексерген: аға оқытушы Секербаева А. Б

Семей 2015 жыл.

Мазмұны:

1. Негізгі бөлім . . . 2

1. 1. Сызықтық буындар . . . 2

1. 2. Динамикалық буынар . . . 3

Қорытынды . . . 5

Әдебиеттер . . . 5

Негізгі бөлім

Буындар сызықты және сызықты емес, инерционды және инерционсыз, аналогтық және дискретті болып бөлінеді. Автоматикалық басқарудың радиоэлектронды жүйелерінде радиотехникалық құрылғыларға сәйкес буындар жиыны қолданылады, олар: жоғары жиілікті және тұрақты токты күшейіткіштері автогенераторлар, модуляторлар және демодуляторлар, фильтрлер, сонымен қатар төмен жиілікті, қосқыштар және дабыл ажыратқыштар, жиілік ауыстырғыштар және түрлендіргіштер, жиіліктік, фазалық және бұрыштық дискриминаторлар, дабылдың жиілігін, фазасы және амплитудасын басқаратын құрылғылар, дабыл тоқтатқыш желілер, параметрлерді өлшейтін барлық сезбек: релейлі, импульсті, сандық.

Бұндай буындардың әрбіреуінің жұмыс талдауы оған сәйкес, дифференциялдық теңдеумен сипатталатын, модельдің негізінде, сонымен қатар белгілі бір параметрлер, сипаттамалар және графиктер жиының көмегімен жүзеге асырылады:

таралу коэффициенті жәен таралатын функция;
буынның жиіліктік қасиеттерін анықтайтын амплитудалық және фаза-жиіліктік сипаттамалар;
буынның уақыттық қасиеттерін анықтайтын өтпелі және импульстік сипаттамалар;
буынның сызықтық емес қасиеттерін анықтайтын амплитудалық және импульстік сипаттамалар;
кірістік әсердің мүмкңн болатын динамикалық диапозоны.

Сызықтық буындар

Сызықтық буынның міндетіне кіріс дабылының параметрлеріне әсер ету жатады. Күшейткіштерде бұл әсер кіріс дабыл қуаьының күшеюімен байқалады, сүзгілерде - оның спектральді құрамының өзгеруімен, ал дифференциалды буындарда - дабылды дифференциалдаумен, интегралдаушы буындарда -интегралдаумен және т. б. сипатталады. Осы тұста барлық жағдайда талдаудың мәніне берілген 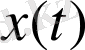кіріс дабылы мен белгілі параметрлер, сипаттамалар немесе дәл осы сызықтық объектінің сызбасы көмегімен 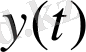шығыс дабылын анықтауда жатыр.

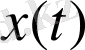пайдалы дабылынан өзге, объектіге бөгеттер де - детерминирлеген немесе кездейсоқ дабыл, әсер етуі мүмкін. Бұл жағдайда бөгеттің 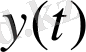шығыс дабылына қалай әсер ететіндігін анықтау қажет. Мысалы, егер объектінің кірісіндегі пайдалы дабыл қуатының бөгет қуатына қатынасы белгілі болса, онда шығысында да дәл сондай қатынаста болады. Сәйкесінше, пайдалы дабылдың да, бөгеттің де сызықтық объекті арқылы өтуін зерттеу қажет.

Сызықтық буынның қасиеті әр түрлі тұрпатпен сипатталуы мүмкін: бір жағдайда оның электрлік сызбасы белгілі, басқа жағдайда - тарату коэффициенті немесе беріліс функциясы белгілі, үшінші жағдайда - жиіліктік немесе уақыттық сипаттамалары белгілі болса, онда оның жұмысын талдауды да әр түрлі әдістермен жүргізуге болады. Сызықтық тізбекті талдаудың шығыс дабылды анықтаумен байланысты бес әдісіне және қысқаша тоқталайық.

1. 2. Динамикалық буынар

Динамикалық буын - ұғымы автоматты басқару теориясына байланысты. Динамикалық жүйенің орнықтылық сипатын анықтау үшін әр түрлі әдістер болуы мүмкін. Келесі анықтамаға тоқталсақ: «қозғалыстың орнықтылығы дегеніміз қозғалатын жүйенің кейбір қозғалыстан, жүйенің бастапқы қалпына (фазалық кеңістікте), жалпы қозғалу заңдылығының да өте аз ұйтқулар барысындағы аз ауытқу қабілеті. Кейде бастапқы қалыптың аз ұйтқулардың кез келгені емес, тек қосымша шартқа бағындырылғандары алынады; кейде ұйтқулардың аздығы мен ауытқуы тек бірнеше параметрлермен өлшенеді».

Кесте 1- Типтік динамикалық буындар сипаттамасы

Буын түрі және оның

беріліс функциясы

Позициялық буындардың уақытша сипаттамалары

Көшу функциясы h ( t )

Функция салмағы w ( t )

Буын түрі және оныңберіліс функциясы:

1. Сәттік

W ( p ) = K

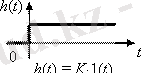
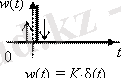
Позициялық буындардың уақытша сипаттамалары: Типовые звенья САУ и их характеристики

Буын түрі және оныңберіліс функциясы:

2. Апериорлық 1- ші

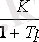
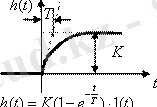
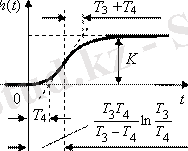
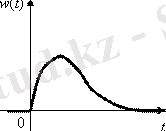
W ( p ) = Типовые звенья САУ и их характеристики

Позициялық буындардың уақытша сипаттамалары: Типовые звенья САУ и их характеристики

Буын түрі және оныңберіліс функциясы:

3. Апериорлық 2- ші

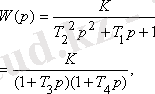
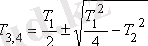
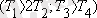
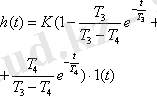
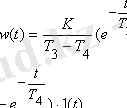
Типовые звенья САУ и их характеристики

Позициялық буындардың уақытша сипаттамалары:

Типовые звенья САУ и их характеристики

Буын түрі және оныңберіліс функциясы:

4. Колебалдық

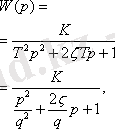
Типовые звенья САУ и их характеристики

q =1 /T

Позициялық буындардың уақытша сипаттамалары:

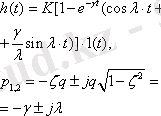
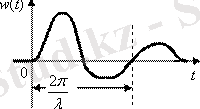
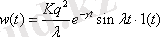
Типовые звенья САУ и их характеристики

Буын түрі және оныңберіліс функциясы:

Бақылау процесінің дифференциалдық теңдеуін төмендегі формула ретінде алынған:

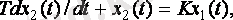Типовые звенья САУ и их характеристики (1. 2. 2)

Мұндағы, T - тұрақты уақыты буыны; K - буынның аударым коэффициенті.

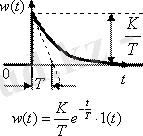
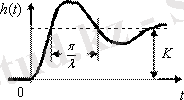
Буынның көшу функциясы h(t) =x2(t) дифференциалдық теңдеудің жалпы және ішінара шешімдер сомасы ретінде алынған (1. 2. 2) нөлдік бастапқы шарттарына және бірыңғай экспозиция қадамға енгізу үшін қолданылады x1(t) =1[t]

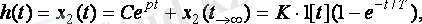Типовые звенья САУ и их характеристики (1. 2. 3)

Мұндағы, p=-1/T -тән теңдеудің түбірі Тр+1=0; С=-K

Қорытынды: Біртекті емес сызықтық дифференциалды теңдеуді шешуге негізделген әдіс. Сызықтық жүйе дифференциалды теңдеумен сипатталады. Mathcad бағдарламасының пакеті кіріс дабылының кез келген қиындығына қарамастан және сызбасы белгілі болған жағдайда тікелей шешуге мүмкіндік береді.

Әдебиет:

1 Абрамов В. М. Электронные элементы устройств автоматического управления. - М. : Академкнига. 2006.

2 Дорф Р., Бишоп Р. Современные системы управления. - М. : Лаборатория базовых данных. 2002.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.