Maple жүйесінде жаратылыстану және экология есептерінің дифференциалдық математикалық модельдерін құру және зерттеу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 45 бет
Таңдаулыға:
Мазмұны
КІРІСПЕ . . . 4
I-ТАРАУ Математикалық модельдеу, оның негізгі ұғымдары мен
әдістері . . . 6
§1 Модель және математикалық модельдеу . . . 8
§2 ҚДТ, оған Коши есебінің қойылуы . . . 10
§3 Дифференциалдық теңдеу құруға келтіретін практиканың
есептері . . . 13
II-ТАРАУ Жаратылыстану есептерінің дифференциалдық
модельдерін құрып-зерттеу . . . 18
§4 Дененің жылу бөле отырып салқындауы туралы есеп . . . 20
§5 Катердің инерция бойынша қозғалысын модельдеу . . . 21
§6 Аварияға ұшыраған сүңгуір қайықтың теңіз қабатта шөгуі туралы
есеп . . . 23
§7 Су қабаттарында жарықтың жұтылуы туралы . . . 25
§8 Химиялық кинетика есептерін модельдеу . . . 26
§9 Жер бетіне құлаған метеордың ақырғы жылдамдығын табу . . . 35
§10 Газдың иондалуы туралы есеп . . . 37
§11 Ауа қысымының барометриялық формуласын қорыту . . . 38
§12 Атылған оқтың қабырғаны тесіп өту уақытын есептеу туралы . . . 39
III-ТАРАУ Экология есептерінің дифференциалдық модельдерін
құрып-зерттеу . . . 42
§13 Биологиялық популяция мөлшерінің динамикасы: Мальтус пен
Ферхгольст модельдері . . . 43
§14 Екі популяцияның тіршілік үшін күресін сипаттайтын В. Вольтерраның модельдері. Стандартты бағдарламаларды қолдану . . . 46
§15Эпидемиялар теориясының есептерін модельдеу . . . 51 §16 Өндірістік цех ауасын желдетіп тазарту есебі . . . 56
§17 Радиоактивтік ыдырау есебін модельдеу . . . 58
Математикалық модельдер бейбітшілік үшін күресте . . . 63
Қорытынды . . . 67
Қосымша:
(а) экология терминдерінің түсіндірме сөздігі . . . 68
Қолданылған әдебиеттер . . . 70
КІРІСПЕ.
Бүгінгі күні орта және жоғары мектепте математиканы оқытуда оның практикаға бет бұра бағдарлануын барынша күшейту мәселесі өз шешімін күтуде. Осы уақытқа дейін қалыптасып үлгерген математиканың мектеп курсындағы, жоғары оқу орындарындағы оқытылатын теориялық және практикалық мазмұндағы оқу материалының диспропорциясы оқушылардың математикалық сауаттылығын, сонымен қатар экологиялық сауаттылықтарын нарықтық қатынастар талаптарына сай деңгейге көтеруге кедергі болуда: оқушылар мен студенттер алған білімін стандартты емес жаңа жағдайларда қолдана алмайды; мазмұнды практика есебінің математикалық моделін құрып-зерттеуде дәрменсіздік танытады; практикалық мазмұндағы есептерді шешуде алгоритмдік сауаттылығын көрсете алмайды; жаңа білімді қалыптастыруда өте қажетті болып есептелетін пәнаралық байланыстарды аңғарып, тиімді етіп қолдана алмайды. Осы тұрғыдан алғанда оқушылар мен студенттерге олардың математикалық білімін физика, биология, химия пәндерімен тығыз байланыста бекіте түсетін, сол салалардан алынған сапалық мазмұндағы білімдерін математикалық методтар арқылы қуаттайтын практикалық мазмұндағы есептерді қарастыру қажеттілігі туындайтыны анық. Бұл екіншіден, ізденуші жастардың экологиялық сауаттылықтарын математикалық методтарды қолдану негізінде көтеруге мүмкіндік береді. Бүгінгі күннің талабына сай осындай оқыту мен зерттеу жұмыстарын компьютерлік математиканың әртүрлі бағдарламалық жүйелерін қолдана отырып жүргізу өзінің тиімділігін дәлелдеп отыр. Бұл жұмыста экология мен жаратылыстану есептерінің дифференциалдық модельдеу методы арқылы компьютерлік математиканың Maple бағдарламалық жүйеcі негізінде қарастырылып шешіледі және әртүрлі жағдайда сапалық талдаулар жасалады.
Дипломдық жұмысым үш тараудан тұрады.
І ТАРАУДА Математикалық модельдеу мен оның негізгі ұғымдары, дифференциалдық теңдеулер теориясынан қажетті мәлімет берілген: модель, оның қажеттілігі, математикалық модельдеу, оның негізгі кластары мен кезеңдері; дифференциалдық теңдеу ұғымы, оның шешімі мен интегралдық қисығы; Коши есебінің қойылуы мен оның геометриялық мағынасы; Коши есебі шешімінің бар және жалғыз болуы туралы негізгі теорема; дифференциалдық теңдеу құруға келтіретін практиканың есептері.
ІІ ТАРАУДА Жаратылыстану есептерінің дифференциалдық модельдерін құрып-зерттеу қарастырылған: дененің жылу бөле отырып салқындауы туралы есеп; катердің инерция бойынша қозғалысы; аварияға ұшыраған сүңгуір қайықтың теңіз қабаттарына шөгуі туралы есеп; жер бетіне құлаған метеордың ақырғы жылдамдығын табу; газдың иондалуы туралы есеп; ауа қысымының барометриялық формуласын қорыту; атылған оқтың қабырғаны тесіп өту уақытын есептеу туралы есептер зерттелген. Бұл есептер өздерінің практикалық құндылығымен қатар, оқытуда пәнаралық байланыстарды іске асыруға және оқушылардың терең білім алуға ынтасын арттыруға оң ықпалын жасайды. Бұл тарауда жинақталған оқу материалын орта мектепте болсын, университет қабырғасында болсын, оқушы-жастардың жаратылыстану пәндерінен сауаттылығын жетілдіруге пайдалануға болады деп есептеймін.
ІІІ ТАРАУДА Экология есептерінің дифференциалдық модельдерін зерттеу қаралған: биологиялық популяция мөлшерінің динамикасы:(Мальтус пен Ферхгольст модельдері) ; екі популяцияның тіршілік үшін күресін сипаттайтын В. Вольтерраның модельдері; (оны шешуге стандартты бағдарламаларды қолдану) ; эпидемиялар теориясының әр түрлі есептерін модельдеу; өндірістік цех ауасын желдетіп тазарту есебі; радиоактивтік ыдырау есептері қарастырылған.
I-ТАРАУ Математикалық модельдеу, оның негізгі ұғымдары
мен әдістері
Модель деген не және бiзге модель не үшiн қажет
Әуелi модель туралы бiрнеше мысалдар келтiрейiк:
а) Архитектор бұрын болмаған үлкен ғимарат-үй салуға дайындық үстiнде, ол алдымен осы ғимаратты кiшкентай кубиктерден тұрғызады;
ә) Лектор адамның қан айналу жүйесiн айтып түсiндiру үшiн плакатқа сызықтар мен стрелкалар арқылы қан айналымы көрсетiлген сурет-схеманы пайдаланады;
б) Өндiрiстен жаңа ұшақ жасап шығару үшiн алдымен конструктор ұшақтың макетiн аэродинамикалық трубада сынап, сәйкес датчиктер арқылы конструкцияның әрбiр бөлiгiне түсетiн қысым шамасын анықтайды;
в) Қабырғада буырқанып жатқан теңiз көрсетiлген сурет iлулi тұр. Осы мысалдардағы модельдiң атқарар ролiнiң қандай екенiн түсiндiрейiк. Архитектор ғимаратты бiрден сала беруiне де болар едi, бiрақ ол ғимараттың қаншалықты әсем болатынына, оның жекеленген бөлiктерiнiң өзара қаншалықты үйлесiм табатындығына көзi жетпегендiктен, алдымен кубиктер арқылы үлгiлер дайындап, тәжiрибе жасайды. Лектор плакатты емес, анатомиялық атласты алуына болар едi, бiрақ бұлай ету оның лекция оқуына кедергi жасайды, себебi атластың тыңдаушылардың негiзгi материалды саралап қабылдауына мүмкiндiк беруi неғайбыл. Сондықтан плакатты пайдалану тиiмдi. Ұшақты сынақтан өткiзбей-ақ өндiрiске жiберуге болар едi, бiрақ ұшақтың бiр тетiгiнде қысым қалыптан жоғары болса, онда ұшып бара жатқан ұшақ апатқа ұшырайды. Сондықтан да ұшақтың макетiн алдын-ала трубада сынаған жөн. Оң эмоциялық толқынысты адам теңiз жағасында тұрып алуына болады. Бiрақ сiз теңiзден алшақ жерде тұрсаңыз немесе теңiз бетi тынық болса, немесе сөз өмiрiнде теңiз көрмеген адамның әсерi жөнiнде болса ше!- онда толқынды теңiз бейнеленген суретке қарау жеткiлiктi. Барлық мысалдарда нақтылы объектiнi оны алмастыратын сәйкес бiр нәрсемен (нысанмен) салыстырып отырмыз: ғимаратты-кубиктерден тұрғызылған ғимаратпен, ұшақтар сериясын-трубадағы жалғыз ұшақпен, қан айналу жүйесiн - плакаттағы схемамен, буырқанып жатқан теңiздi -суретпен. Барлық жағдайда да белгiлi бiр қасиеттiң екiншi бiр түрге өткенде де сақталып отырғандығы байқалады: кубиктерден құралған ғимарат нағыз ғимараттан көптеген есе кiшi болғанымен, оның сыртқы түрi - сәулетi туралы мәлiмет бере алады. Плакаттың тканьдер мен тiрi организм жүйесiмен еш байланысы болмаса да, қанның қай бағыттарда ағатыны жөнiнде тура мағлұмат бередi. Аэродинамикалық трубадағы ұшақ ұшпаса да, ондағы пайда болатын қысымдар картасы ұшақтың ұшу шарттарына сәйкес келедi. Сурет пен теңiздiң физикалық кейпi бiрдей болмағанымен, олар бiр-бiрiне ұқсайтын әсер қалдырады.
Модельдi құру, зерттеу және қолдану процесiн модельдеу деп атайды . Модельдеудiң басты өзгешелiгi оның көмекшi объект-үлгiлер арқылы танудың методы болуында. Модельдеу методын қолдану қажеттiлiгi көптеген жағдайда объектiлердi (немесе оларға тиiстi проблемаларды) тiкелей зерттеу мүмкiн болмауымен (мысалы, Жердiң ядросы, немесе Әлемнiң алыс түкпiрлерi), я олардың нақты туындамауымен (экономиканың болашақ күйi, қоғамның келешектегi сұранымдары, т. б. ), не болмаса оларды зерттеуге өте көп уақыт пен қаржы қажет болуымен (мысалы, су электр станциясын салуға байланысты) анықталады.
Анықтама:
Модель дегенiмiз танып-бiлу (зерттеу) процесiнде обьект - оригиналдың орнына ұсынылатын, оның басты маңызды қасиеттерiн сақтайтын, материалдық немесе ой түрiндегi обьект-үлгi (кескiн) .
Жаңа конструкцияларды, жаңа жобаларды құруда модельді пайдаланады. Жақсы құрылған модель зерттеу барысында көптеген жеңiлдiктер әпередi. Обьект моделiн басқарудың әртүрлi нұсқаларын жасай отырып, обьектiнiң өзiн дұрыс басқаруды үйренуге болады. Сонымен модель бізге не үшін керек:
1) Нақты обьектiнiң қалай жасалғанын түсiну үшiн, оның құрылымы, негiзгi қасиеттерi, даму заңдылықтары және қоршаған ортамен өзара байланысы қандай екендiгiн бiлу үшiн қажет;
2) Обьектiнi (немесе процестi) басқаруды үйрену үшiн және берiлген белгiлерi мен мақсаты бойынша басқарудың ең тиiмдi жолдарын анықтау үшiн қажет;
3) Таңдалған жолдарды iске асырудың және обьектiге ықпал етудiң формаларының тура және жанама салдарын болжау үшiн қажет.
§1 Модель және математикалық модельдеу.
Ендi математикалық модельдеу деген не, соған тоқталайық. Табиғаттың кезкелген құбылысын қандай да бiр материалдық системаның өзгеруi деп түсiнген жөн. Осындай әрбiр өзгерiске сәйкес нақты бiр процесс жүредi, ал оның барысында осы системаның қалып - жағдайын сипаттайтын айнымалы шамалар өзгерiске ұшырап отырады. Бұл шамаларды режим параметрлерi деп атайды. Егер нақты бiр құбылысты (процестi) анықтайтын параметрлер жиынтығы үшiн оның математикалық сипаттаушы өрнегi белгiлi болса, онда осы құбылыстың (процестiң) ұқсастық критерийлерi де табылады, сөйтiп осы құбылыстың математикалық моделi болып табылатын қандай да бiр теңдеулер не қатыстар алынады. Обьектiнi зерттеу әртүрлi математикалық методтарды пайдалану нәтижесiнде құрылған математикалық модель арқылы жүргiзiледi. Модельдеу арқылы қазiргi кезде түрлiше күрделi техникалық агрегаттардың: бу қазандары мен турбиналардың, атомдық станциядағы реакторлар мен сұйық металдарды айдайтын насостардың, вентиляциялық қондырғылардың және тағы басқалардың жұмыстарын алдын-ала зерттеуге болады. Электронды есептеу техникасының (ЭЕТ) соңғы кездерi жедел қарқынмен дамуына байланысты, математикалық модельдеу әдiсi өте қуатты зерттеу методына айналып отыр. Бұрындары әлiмiз келмеген көптеген есептердi зерттеп шешу мүмкiндiгi пайда болды. Дәл қазiргi кезеңде математикалық модельдеу, зерттеушiнiң - адамның таланты мен тәжiрибесiне негiзделген эвристикалық әдiстермен толыға келе, имитациялық математикалық модельдеу дегенге айналып отыр. Математикалық модельдеудiң классикалық бiр мысалы ретiнде механикадағы Ньютон заңдарының өздерiмiзге мектептен белгiлi формулалармен берiлуiн атауға болады.
Ендi математикалық модельдердiң негiзгi кластарын атайық:
1) Дескриптивтiк модельдер.
Дескриптивтiк сөзi ағылшынның description сөзiнен шыққан және сипаттау деген мағынаны бiлдiредi. Бұл класқа жататын математикалық модельдер әртүрлi процестердi сипаттауға арналады, және нәтижесiнде осы процестердi басқаруға қажеттi мәлiметтер жинақталады;
2) Оптимизациялық модельдер.
Қандайда бiр процестi немесе объектiнi мақсатты түрде басқару барысында қандай әрекеттер жақсы, ал қандайлары нашар нәтижелер беретiнiн анықтауға және салыстыруға мүмкiндiк бар болса, әрбiр әрекеттiң нәтижесiн сандық тұрғыдан бағалау мүмкiн болса, онда мұндай есептердiң оптимизациялық модельдерi құрылады;
3 ) Көпкритерийлi модельдер.
Бiрнеше мақсаттық функциялары бар (яғни зерттеу процесiнде бiрнеше мақсаттарға жету көзделетiн) болатын есептер үшiн көпкритерийлi модельдер құрылады;
4) Ойындық модельдер.
Мұның алдындағы модельдердiң бәрiнде шешiм қабылдайтын тұлғаға қарсы әрекет ететiн күштер жоқ болатын. Ал шындығына келсек, әртүрлi қатысушы жақтары өзара келiспейтiн мүдде ұстанатын жағдайлар өте жиi кездеседi, бұларды әдетте даулы жағдайлар деп атайды. Осындайда ойындық модельдер құрылады.
5) Имитациялық модельдер.
Математикалық модель құрылып болған соң, оны тиiстi аналитикалық немесе есептеу методтары арқылы зерттеу процесi басталады, сөйтiп модельге қойылатын сұрақтарға жауаптар iзделiнедi. Егер модель жақсы құрылған болса, онда ол арқылы алынатын жауаптар модельденген системаның сәйкес сипаттарымен үйлесiмдi болады. Мүлдем, бұл жағдайда кейде модель арқылы бiзге негiзгi система туралы бұрын белгiсiз болып келген жаңа деректер ашылады. Ал егер құрылған модель нашар болса, онда ол әрi қарай жетiлдiрiлуi немесе басқамен алмастырылуы тиiс. Не дегенде де, модельдi жақсарту процесiнiң қашан аяқталатынын, оның сапалылығын анықтайтын жалғыз критерий-практика болмақ.
Бiз қоршаған нақтылы Әлемдi зерттеу - тану барысында құрылған математикалық модельдердiң дербес түрi ретiнде дифференциалдық модельдердi қарастыратын боламыз.
Анықтама.
Қандайда бiр нақтылы құбылыс немесе процестi зерттеу нәтижесiнде алынатын дифференциал теңдеуге немесе осындай теңдеулердiң жүйесiне қойылған Коши есебiн осы құбылыс не
процестiң
дифференциалдық моделi
деп атайды.
§2 Қарапайым дифференциалдық теңдеу,
оған Коши есебінің қойылуы
Дифференциал теңдеу деп тәуелсіз айнымалы х пен ізделінді функция у-ті, оның қандайда бір n-ші ретке дейінгі туындыларын байланыстыратын
 (1)
(1)
түріндегі қатысты айтамыз. Жалпы дифференциал теңдеу деп құрамында тәуелсіз айнымалылар мен ізделінді функция және оның туындылары бар болатын теңдікті айтамыз.
Дифференциал теңдеу енген функция туындыларының ең жоғарғы ретін дифференциал теңдеудің реті деп атайды. Тәуелсіз айнымалы біреу ғана болса, онда теңдеу қарапайым дифференциалдық теңдеу (ҚДТ) деп аталады.
Дифференциал теңдеудің шешімін табу процесін осы теңдеуді интегралдау дейді. Теңдеудің шешіміне сәйкес сызықты осы дифференциал теңдеудің интегралдық қисығы дейді.
Дифференциалдық теңдеулер математиканың көптеген салаларымен қатар, механика, физика, астрономия, экономикада өте жиі қолданылады. Алдағы тарауларда дифференциал теңдеулерді құруға және оларды зерттеуге келтіретін практиканың есептерін қарастырамыз.
Дифференциалдық теңдеулерге тән қасиет олардың шешімдерінің шексіз көп болуында. Дифференциалдық теңдеудің шешімі ретінде нақты формула тапқан болсақ, онда теңдеудің жалпы шешімін таптық дейміз. Жалпы шешімдегі тұрақтыға белгілі бір сандық мән бергенде алынатын әрбір шешімді дифференциалдық теңдеудің дербес шешімі дейміз.
Практиканың нақты қолданыстағы есептерін шешуде, қандайда бір бастапқы шартты қанағаттандыратын дербес шешімді табу керек болады.
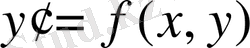 (2)
(2)
теңдеуіне Коши есебі былай қойылады: (2) теңдеуінің барлық шешімдерінің ішінен x=x 0 болғанда y=y 0 мәнін қабылдайтын y=y(x) шешімін табу керек, мұндағы x 0 , y 0 сандары есептің бастапқы берілімдері, ал
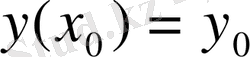 (3)
(3)
шарты есептің бастапқы шарты деп аталады.
Егер х
0
нүктесiнiң қандайда бiр аймағы табылып:
1) бұл аймақта х
0
, у
0
бастапқы берiлiмдерi бойынша шешiм анықталса;
2) х
0
нүктесiнiң аталған аймағында х
0
, у
0
бастапқы берiлiмдерiмен анықталған есептiң басқадай шешiмi болмаса, онда х
0
, у
0
- бастапқы берiлiмдерiмен анықталған Коши есебiнiң шешiмi жалғыз болып табылған деймiз.
Коши есебiне геометриялық мазмұн беруге болады: (1 ' ) теңдеуiнiң барлық интегралдық қисықтарының iшiнен жазықтықтың берiлген М 0 (х 0 , у 0 ) нүктесi арқылы өтетiнiн табу керек, яғни iзделiндi у = ϕ (х) интегралдық қисығы М 0 (х 0 , у 0 ) нүктесi арқылы өтуге тиiс.
Коши есебi шешiмiнiң жалғыздығы туралы мәселе дифференциал теңдеулер теориясында, практикалық қолдануларында өте маңызды роль атқарады. Өйткенi қойылған Коши есебiнiң шешiмi жалғыз болған жағдайда бiз табиғаттағы (өндiрiстегi) сәйкестi құбылыстың (процестiң) берiлген теңдеу мен бастапқы шарттар арқылы анықталған нақтылы және жалғыз заңын алатын боламыз.
(2) теңдеуiн қарастырайық. Осы теңдеудiң оң жағындағы f (х, у) функциясы қандайда бiр G облысында анықталған және үздiксiз болсын деп ұйғарсақ, онда бұл теңдеу белгiлi бiр бағыттар өрiсiн анықтайтын болады және бұл өрiс те үздiксiз болады. Теңдеудiң интегралдық қисығының әрбiр нүктесiнде жүргiзiлген жанаманың бағыты мен өрiстiң бағыты бiрдей болатын ерекше қасиетiн пайдаланып, G облысынан алынған х 0 , у 0 бастапқы берiлiмдерi үшiн Коши есебiнiң шешiмiн жуықтап табуға болады. Ол үшiн “Эйлер сынықтарын” жүргiзу әдiсi қолданылады . Коши есебiнiң шешiмi бар болуы үшiн, (2) теңдеуiнiң оң жағындағы f (х, у) функциясының (х 0 , у 0 ) нүктесiнiң маңайында үздiксiз болғаны жеткiлiктi, осындай жағдайда iзделiндi шешiм тәуелсiз айнымалының бастапқы х 0 мәнiнiң қандайда бiр кiшкене маңайында анықталады және үздiксiз дифференциалданады.
Негiзгi теорема:
Егер (2) теңдеуiнiң оң жағы болатын f (х, у) функциясы G облысында анықталса, және осы облыста мынадай екi шартты қанағаттандырса:
1) f (х, у) үздiксiз болса,
2)

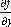
 K, мұндағы К-тұрақты оң сан, онда (2) теңдеуiнiң (3) бастапқы шартын қанағаттандыратын
K, мұндағы К-тұрақты оң сан, онда (2) теңдеуiнiң (3) бастапқы шартын қанағаттандыратын
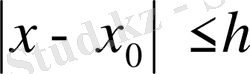 интервалында анықталған (және үздiксiз дифференциалданатын) жалғыз шешiмi бар болады.
интервалында анықталған (және үздiксiз дифференциалданатын) жалғыз шешiмi бар болады.
§3 Дифференциалдық теңдеу құруға келтіретін
практиканың есептері
1. Резервуарда құрамында в кг тұзы бар а кг тұздың сулықоспасы бар. Резервуарға үзіліссіз секундына с кг қоспасын алап тастайтын белгілі уақытта құрылғы қосылады. Сонымен қатар резервуардағы сұйық үзіліссіз араласып тұрады. Резервуардағы тұз саны уақыт бойынша қалай өзгереді?
Шешуі:
Процестің басталу мезетін t уақыттың бастапқы санағы ретінде қабылдаймыз. y(t) - t әр мезетінде резервуардағы тұздың мөлшерін өрнектейтін ізделінді функция. Есептің шарты бойынша және уақыт санағының келісімімен
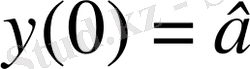 . Бұл әзірге ізделінді функцияның жалғыз белгілі мәні. Есептің негізгі қиындығы қоспаның концентрациясының үзіліссіз өзгергендігі. Шешудің дұрыс әдісін қолданып бұл үзіліссіз өзгеруін пайдалануға болады. Резервуарда кішкене уақыт аралығында
. Бұл әзірге ізделінді функцияның жалғыз белгілі мәні. Есептің негізгі қиындығы қоспаның концентрациясының үзіліссіз өзгергендігі. Шешудің дұрыс әдісін қолданып бұл үзіліссіз өзгеруін пайдалануға болады. Резервуарда кішкене уақыт аралығында
 ие болады. Аралықтың басында резервуарда y(t) кг тұз бар, ал соңында
ие болады. Аралықтың басында резервуарда y(t) кг тұз бар, ал соңында
 кг.
кг.
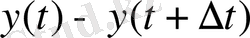 айырымы
айырымы
 уақытындағы қоспамен бірге ағып кеткен тұздың саны. Қоспа концентрациясы қарастырылған уақыт аралығында кемімелі
уақытындағы қоспамен бірге ағып кеткен тұздың саны. Қоспа концентрациясы қарастырылған уақыт аралығында кемімелі
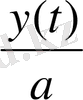 - дан
- дан
 дейін,
дейін,
 болады, бұл теңсіздіктер өзгермейтін болып табылады, егер
болады, бұл теңсіздіктер өзгермейтін болып табылады, егер
 және
және
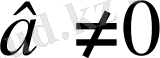 . Бұл теңсіздікті
. Бұл теңсіздікті
 -ға бөліп,
-ға бөліп,
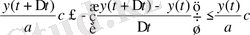 (4)
(4)
Қарастырылған процесстің мінезінен
 ізделінді функция үзіліссіз екенін қорытуға болады. Бұл жағдайда
ізделінді функция үзіліссіз екенін қорытуға болады. Бұл жағдайда
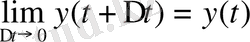 . Онда (4) -тен мынаны табамыз:
. Онда (4) -тен мынаны табамыз:

Ізделінді y(t) функциясы t әр нүктесінде мына туындыға ие болады:
 (5)
(5)
y(t) функциясы (5) -ші теңдеуді қанағаттандырады. Бұл теңдеу
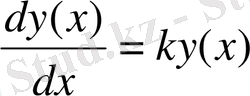 теңдеуімен пара-пар, сондықтан
теңдеуімен пара-пар, сондықтан
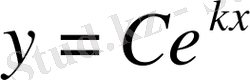 (
(
 ) теңдеуін ескеріп және y(0) =
в
шарты бойынша, резервуардағы тұздың санының уақытта өзгеруін суреттейтін ізделінді функция мына түрде болады:
) теңдеуін ескеріп және y(0) =
в
шарты бойынша, резервуардағы тұздың санының уақытта өзгеруін суреттейтін ізделінді функция мына түрде болады:
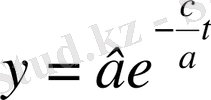 .
.
2. Қайықтың жылдамдығына пропорционал су кедергісінің әсерінен қайық өз қозғалысын баяулатады. Қайықтың бастапқы жылдамдығы 2м/с тең, ал оның жылдамдығы 4 с кейін 1м/с тең болады. Қанша секундтан кейін қайықтың жылдамдығы 0, 25м/с тең болады? Қайық тоқтауына дейін қанша жол жүреді?
Шешуі
:
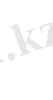
 t мезетіндегі қайықтың жылдамдығы болсын. Онда
t мезетіндегі қайықтың жылдамдығы болсын. Онда
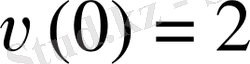 . Ньютонның екінші заңына сәйкес
. Ньютонның екінші заңына сәйкес
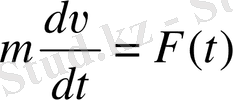 , F(t) - қайыққа әсер ететін күш; m - қайықтың массасы. Шарт бойынша
, F(t) - қайыққа әсер ететін күш; m - қайықтың массасы. Шарт бойынша
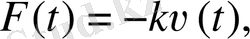 k>0 -
пропорционалдық коэффициент, минус таңбасы күш қозғалысқа қарсы бағытталғанын көрсетеді. Сондықтан қайық қозғалысының дифференциалдық теңдеуі:
k>0 -
пропорционалдық коэффициент, минус таңбасы күш қозғалысқа қарсы бағытталғанын көрсетеді. Сондықтан қайық қозғалысының дифференциалдық теңдеуі:
,
оның шешімі
 .
.
Шарт бойынша
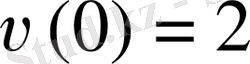 , сондықтан C=2 және
, сондықтан C=2 және
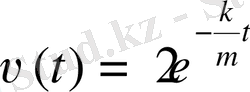 .
.
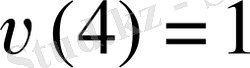 болған соң,
болған соң,
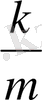 шаманы былай анықтауға болады:
шаманы былай анықтауға болады:
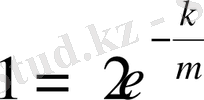 ;
;
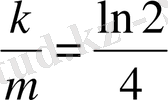 .
.
Қайық жылдамдығы
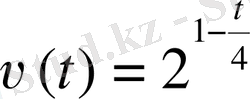 . Қайық жылдамдығы 0, 25м/с болатын Т уақытын мына теңдеу арқылы табамыз:
. Қайық жылдамдығы 0, 25м/с болатын Т уақытын мына теңдеу арқылы табамыз:
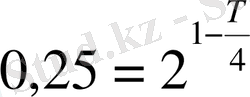 ,
,
 ,
,
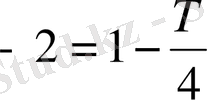 , T=12c.
, T=12c.
Қайықтың жүрген жолының ұзындығын мына формула арқылы есептейміз:
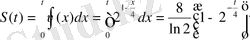 .
.
Көрініп тұрғандай қайықтың жүрген жолы мына мәннен үлкен бола алмайды
 м.
м.
3. Шеңбер формалы виктория-регия жас жапырағының үлкею жылдамдығы оған түсетін күн сәулесінің санына және жапырақ радиусына пропорционал. Күн сәулесінің саны жапырақтың ауданына және сәулелердің бағытының арасындағы косинус бұрышына пропорционал. Егер таңғы сағат 6 00 -да ауданы 1600 см 2 , ал сол күні сағат 18 00 -да ауданы 2500см 2 болса, онда жапырақтың S ауданы мен t уақытының арасындағы байланысты табу керек. Күн сәулесі мен вертикаль бағыты арасындағы бұрышты таңғы сағат 6 00 және 18 00 -де 90 0 тең, ал түсте - 0 0 .
Шешуі
: S=S(t) t уақыт мезетіндегі жапырақтың ауданы. Егер уақыт санағының бастапқысы ретінде таңғы сағат 6
00
-ді алсақ, онда S(0) =1600 см
2
, ал S(12) =2500cм
2
(18
00
-гі жапырақтың ауданы) . Жапырақтың өсу жылдамдығы
 , k - пропорционалдық, r - жапырақтың радиусі, Q - күн сәулесінің саны. Шарт бойынша
, k - пропорционалдық, r - жапырақтың радиусі, Q - күн сәулесінің саны. Шарт бойынша
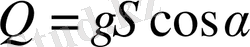 , γ - пропорционалдық коэффициенті, α - күн сәулесінің және вертикальдің жапыраққа бағытының арасындағы бұрыш. α=α(t) бұрышы уақыттың сызықтық өспелі функциясы болып табылады:
, γ - пропорционалдық коэффициенті, α - күн сәулесінің және вертикальдің жапыраққа бағытының арасындағы бұрыш. α=α(t) бұрышы уақыттың сызықтық өспелі функциясы болып табылады:
 ,
,
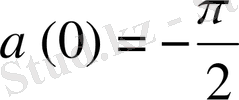 ,
,
 ,
,
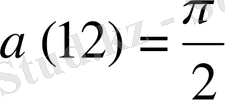 .
.
Көрсетілген шарттардан табатынымыз:
 ,
,
 ,
,
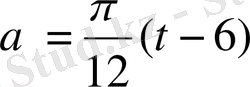 . Сондықтан
. Сондықтан
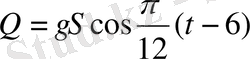 , жапырақтың радиусы
, жапырақтың радиусы
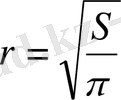 болған соң,
болған соң,
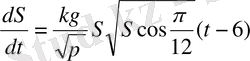 .
.
Айнымалыларды бөліп және интегралдап,
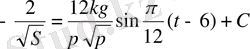 ,
,
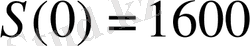 ,
,
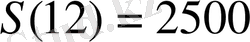 шарттарынан
шарттарынан

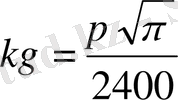 .
.
Бұл мәндерді соңғы теңдікке қойсақ:
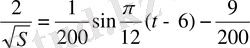 ,
,
немесе
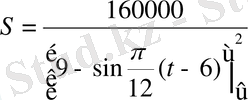
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz