Автоматты басқару теориясы пәнінен курстық жұмыс

Мазмұны

Кіріспе

Басқару ғылымы жайлы білім беретін ғылыми пәндерге «Автоматты басқару және реттеу теориясы»да кіреді. Алғашында ол автоматты басқару процесстерінің динамикасы мен статикасын игеруге құрылған және оны техникалық, өндірістік, транспорттық, энергетикалық және т. с. с нысандармен құрған. Оның негізгі мәндері қазіргі уақытқа дейін сақталынған. Дегенмен, қазіргі кезде оның шешімдері мен нәтижелерін басқару жүйесінің динамикалық қасиеттерін зерттегенде техникалық ғана емес, сондай-ақ экономикалық, ұжымдық, биологиялық сипатттарын да ала алады.

Техникалық процесс арқылы автоматты басқаруды жүзеге асыру үшін басқару нысанынан және онымен байланысқан басқару құрылғысынан тұратын жүйе құрылады. Қандай да техникалық жабдық сияқты, бұл жүйе конструкциясы мықты және динамика тұрғысынан төзімді болуы керек. Осы аталған нағыз механикалық терминдер бұл жағдайда бірнеше шарттарға жүгінеді. Олар бойынша жүйе өзіне берілген функцияны инерционды сипаттары мен қашып кете алмайтын бөгеттерге қарамастан дәл орындалуы керек дегенді білдіреді. Жүйе конструкциясы мықты және динамика тұрғысынан төзімді болып тұрғанда, автоматты түрде реттеу қажеттігі туындамайды.

Реттеулерді құру қажеттігімен, ең бірінші жоғары дәлдікті механизм құраушылары (бірінші кезекте сағат) кезіккен. Тіпті өте кішкентай, бірақ үзіліссіз әсер етіп тұратын бөгеттер жинала-жинала дәлдік шарттарына бағындырмай қалыпты жұмысты бұзған. Оларға конструкциялық жабдықтарын, мысалы, дәлдікті жақсарту, детальдарды өңдеу тазалығы арқылы қарсы тұру әрдайым мүмкін бола бермеді және дәлдікті арттыру үшін сағаттардың құрамына реттеуіштерді енгізе бастады. Біздің дәуірімізде арабтар су сағаттары деңгейінде қалқымалы реттегіштерді жетілдірді. 1675 жылы Гюйгенс сағат жүрісіне маятникті реттеуіш енгізді.

Реттегіштерді құру қажеттігін туғызған тағы да бір себеп: өте күшті бөгеттердің әсерінен бұзылған процессті басқару қажеттігі болды. Осы кезде тек дәлдік қана емес, сонымен қатар жүйенің жалпы жұмыс қабілеттілігі бұзылған. Осындай реттегіштердің ізін салушылар қатарына сулы ұн тартатын диірмендердің жұмыс жылдамдығын центрден тепкіш маятникті теңестірушіні жатқызуға болады. Бірақ, жеке автоматты реттеулер ерте кездерде пайда болған, олар тарихи оқиғаларда ғана қызықтырушы болып қала берді, және техникалық құрылуы мен Автоматты басқару теориясына еш әсерін тигізген жоқ. Осы бағыттың шалқып дамуы тек XVIII ғасырда және XIX ғасырда Еуропадағы өнеркәсіп аударыс дәуірінде басталды.

Осы периодтың бірінші ойлап табылған реттеуіші 1765 жылы Барнаулда Ползунов құрастырған булы машинаның қазаның қуат көзін автоматты қалқымалы реттеушісі; 1788 жылы англиялық механик Дж. Уатт жасаған булы машина жылдамдығын центрден тепкін реттеушімен реттеу;

1808 жылы Жаккарт ойлап тапқан перфокартадан тоқыма станогын басқарудың бағдарамалық құрылғысы жатады. Осы реттеуіштер XX ғасырдың ортасына

дейін жалғасқан реттеуіштер мен реттеу принциптерін ойлап табудың ағынына жол ашты. Осы периодта туынды әсер бойынша (Сименсев ағайындар) жүк бойынша (инженер Ж. Понселе), қатқыл кері байланысы бар электр жүргізгіші бойынша (инженер Л. Фарко), иілгіш кері байланысы бар реттегіштер (изодромды), «буды алып тастауға» импульсті реттегіштер пайда болды.

Булы машина өздігінен жұмыс тұрақтылық қабілеті болмағандықтан және «өзін өзі теңестіруі» болмағандықтан техникада қолданыста және реттеу теориясында кездейсоқ бірінші нысан болған жоқ. Оның қолайсыз диамикалық сипаттары құраушы күткендей оған қосылған реттеуіш жұмысын дұрыс жасап отырмады, ол машинаны «тербетті» немесе оны мүлде басқаруға жарамсыз етті. Осының барлығы теориялық зерттеулер жүргізуді талап етті. Бірақ өткен ғасырдың 60-шы жылдарының аяғына дейін реттеудің теориялық зерттеулері бүгінгі күні біз «жүйелік келтірімнің жоқтығы» деп атап жүргеннің болмауымен ерекшеленеді. Зерттеушілер техникада жаңа бағыттың туындап жатқанын сезінбеді. Олар реттеушілерді машинаға тек қосалқы шылау ретінде ғана деп санады, маховик функцияларын қайталайтын «модераторлардың», «жүріс теңестірулерінің» жабдықтық көптүрлілігі деп санады. Көптеген жұмыстарда идеалды инерциясыз реттегіштер қарастырылған. Реттеуіштердің динамикасын есепке ала отырып қарастырылған жұмыстар бір адым жақсы деп саналған, бірақ ол кездері реттеуіштер машинадан жеке дара түрде қарастырылған. Көптеген авторлар реттеуіштердің өзінің тербелісін тоқтатуды көздеген, себебі олар осыны жүзеге асырсақ, машина жұмысы да жақсы қызмет атқаруына жеткілікті деп есептеген. Теориялық зерттеулерге осындай көзқараспен келу жаңа ғылым үшін негіз бола алмады, олар тек қолданбалы механикада булы машиналар бөліміне жай ғана қосымша ретінде ғана жарамды болды.

Келеңсіз жағдайға және зерттеу әдістемесіне 3 фундаментальды жұмыс түбегейлі өзгеріс енгізді. Осы жұмыстар жаңа ғылым мазмұны болды: Дж. Максвеллдің «О регуляторах» (1866 ж. ) және Вышнеградскийдің «Об общей теории регуляторов» (1876 ж. ) және «О регуляторах прямого действия» (1877 ж. ) жұмыстары. Максвелл және Вышнеградский реттеуіш пен машинаны біртұтас динамикалық жүйе ретінде қарастырып келеңсіздік жағдайына жүйелі жол тапты. Олар кіші тербелістерді зерттеді және жүйенің күрделі дифференциалды теңдеулерін сызықты етті. Осының арқасында конструкциялары мен әсер принциптер бойынша әртүрлі жүйелерді зерттеудің әдістемелік жолын табуға және тұрақтылық теориясының негізін салуға және де кері байланыс принципі бойынша реттеудің маңызды заңнамаларын орнатуға мүмкіндік туды. Сол кезде айырықша маңызды рөлді Вышнеградскийдің еңбегі атқарды. Ол терең инженерлік көқараспен, сол кездердің техникасы үшін маңызды нысандарды қарастырумен, бағалы

тәжірибелік ұсыныстарды қамтумен және реттеу сапасын зерттеудің қазіргі әдістер қатарын бастаумен ерекшеленеді. Сондай-ақ оның еңбегінде тұрақтылық диаграммасы, түбірлерді орналастыру, монотондылық және орнықтылық аудандарын белгілеу қарастырылған. Сондықтан Вышннеградскийдің замандастары оны автоматты реттеу теориясының негізін қалаушы деп санады.

Сол кездері Дж. Максвелл еңбегі елеусіз қалды, себебі ол жұмыста көптеген инженерлердің тобына қызықсыз нысандарды қарастырды, нақты тәжірибелік тұжырымдар жасалынбады және тіпті ойша түрде сол кезде ойлап табылған машиналарға жарамсыз астатикалық реттеуіштерді ұсынды. Бұл жұмыстың рөлі тек автоматты реттеу теориясы жалпы ғылыми пән ретінде қалыптасқан соң ғана бағаланды.

Ерте кездердің өзінде -ақ реттеу теориясы математикалық жоспарларды өңдеуге себепші бола бастады. Максвеллдің ұсыныстары бойынша Раус сипаттамалық теңдеу мен орнықтылықтың түбірлер орналасуын бағалау алгоритмін құрды. А. Стодолдың сұрауы бойынша Гурвиц орнықтылықтың детерминантты критерийін жазды. Словак инженері және ғалымы болып табылатын Стодолдың жұмытары реттеу процессіне ұзын құбыр әсерін ескере отырып, булы және гидравликалық турбиналардың орнықтылық теориясында үлкен орын алды.

Осы теорияға Н. Е. Жуковский зор салым салды. Ол «О прочностити движений» еңбегінің және «Теория регулирования хода машин» (1909 ж. ) алғаш орыс тіліндегі оқулықтың авторы. Жуковский ұзын құбырлардағы процесстерге құрғақ үйкеліс әсерін қарастырды, кейбір теңдеулердің соңғы қалдықтағы жабдықтармен импульсті реттеу процесстерін зерттеді.

XX ғасырдың басындағы бірінші онжылдықтың ішінде автоматты реттеу тоериясы, қолданбалы бөлімдер жанынан жалпы пән ретінде құрылды. Ол бөлімдерге, мысалы, электрлі жүйелер мен машиналарды реттеу-Х. Томның (1914 ж. ), Р. Жюильяр (1933 ж. ), В. С. Кулебакин (1926 ж. ), С. А. Лебедев және П. С. Жданов (1932 ж. ), Н. М. Крылов және Н. Н. Боголюбов (1932 ж. ) ; қозғалтқыштарды реттеу-М. Толле (1905 ж. ), У. Тринкс (1919 ж. ) ; жылулық және булы күшті орналастыруларды реттеу - Т. Штейн (1926 ж. ), Г. Вюнш (1930 ж. ), Ю. Г. Корнилов және В. Д. Пивень (30-шы жылдары) ; булы турбиналарды реттеу-А. В. Щегляев (1933 ж. ) ; әртүрлі өндірістік процесстерді реттеу -В. Оппельт (1939 ж. ) және т. б. Жалпы техникалық сипаттағы пән ретінде реттеу теориясы бойынша И. Н Вознесенскийдің (1922-1949 жж. ) еңбектерінде айырықша нақты ойлар келтірілген.

Жүйенің процесстер интенсивтілігінің жоғарлатуымен байланысты, сапаға және дәлдікке талаптар, жылдамдықтар сияқты қиындықтар зерттеудің әсерлі әдістерін құру қажеттігін тудырады. Зерттеушілердің ойы аналитикалық және графикалық көрнекілікті алуға байланысты жиіліктік сипаттамаға ауады және осы арқылы тәжірибелік және теориялық зерттеу әдістерін алуға болады. Осы кездері Х. Найквистің (1932 ж. ) жұмысы пайда болды: тұйықталған жүйенің жиіліктік сипаттамасына негізделген

радиотехникалық кері байланысты күшейткіштердің орнықтылық критерийлері қарастырылды; сонымен қатар, А. В. Михайловтың «Горманический метод в теории регулирования» (1938 ж. ) жұмысы: реттеу теориясында жиіліктік әдістерді қолдану мақсаты талқыланған және реттеу шынжырын алдын-ала ажыратуды талап етпейтін жаңа критерий ұсынылады. Найквист пен Михайлов әдістері іс - тәжірибиеге тек соғыс жылдарынан кейін ғана кірді. 1946 жылы Г. Боде және Л. Мак-Кол жиіліктік логарифмдік сипаттама жүргізді. Флойд сапаны зерттеу үшін ақиқат жиіліктік сипаттамалы трапеция сомасымен аппроксимирлеуді ұсынды. Г. Браун, А. Холл, Д. Кемпбелл, Г. Честнат, В. В. Солодовниковтар синтездің жиіліктік әдісі мен жүйе есебін, оларға инженерлік есептерге ыңғайлы форма беру арқылы өңдеуді аяқтады.

1940-50 жылдары сызықты емес жүйелер теориясының негіздері өңделді. Бұл тапсырма сызықтық емес тапсырмаларға арналған бірыңғай математикалық аппараттың жоқтығынан қиындай түсті. Осы бағытта тек қана көптеген жекеше сызықтық емес жүйелердің түрлерінен тарылған класстарды зерттеу үшін таңдалып алынғанда ғана алдыға жылжу мүмкін болды. Оларды тәжірибиеде кең қолданысқа иелерін таңдап алды, яғни бөлікті: сызықты динамикалық және сызықты емес статикалықты көрсетуге байланысты жүйелерді таңдап алды. Сызықты емес статикалық сипаттамалардың бөлшек-сызықты аппроксимациялары терең детальді түрде зерттелді.

Сызықты емес бөліктің аналитикалық сипаттары мен сызықты емес жүйенің орнықтылығын зерттеудің маңызды бағыты А. А. Ляпунов (1896 ж. ) жұмыстарына негізделген. СССР кезінде ол А. И. Лурье (1944-1951), және А. М. Летов (1955) жұмыстарында өркендеді. Осы бағыттың соңғы кезеңі ретінде абсолютті тұрақтылық теориясының өңделуін есептеуге болады. Келеңсіздіктер А. И. Лурье және В. И. Постников арқылы жойылды. Тереңірек М. А. Айзерман (1949, 1963) өңдеді және өте көркем шешімді румындық ғалым В. М. Попов (1959) шығарды. Ол келешекте сызықты емес жүйелерде осы әдістерді қолдануға мүмкіндік берген жиіліктік көріністерді қолданды. Сызықты емес жүйелерді сапалы зерттеу үшін фазалы кеңістіктер мен жазықтықтарда траекториялар арқылы өтпелі процесстер көрінісіне шоғырланатын әдістер үлкен мағынаны қамтиды. Осы бағыттың негізін Андронов және 1930-40 жж. оның мектебінде салынған. Үлкен көркемділікті және барлық мүмкін қозғалыстардың жиынтығын қамтитын фазалық жазықтық әдісі екінші ретті теңдеумен шектелінетіне қарамастан сызықты емес жүйелерде процесстердің сипаттамалық ерекшеліктерін ашуға мүмкіндік берді: шекті циклдер, сырғанақ режимдер, ексіту және т. б. Көпөлшемді фазалық жазықтықтарды аналитикалық зерттеу әдісі мен фазалық көріністер үйлесімі нысан параметрінің көптеген өзгерістері негізінде жұмыстың жоғары сапасын сақтап отыра алатын айнымалы структурасы бар жаңа маңызды жүйе класстарын ұсынып және зерттеуге мүмкіндік берді. Бұл жұмыс 1917 жылы Ленин сыйлығымен марапатталған.

Я. З. Цыпкин әртүрлі модуляция түрлері бар жүйелердің релейлі (1955) және импульсті (60-шы жылдары) теорияларының негізін салды. Осы жұмыстар циклы 1960 жылы Ленин сыйлығымен марапатталған.

Автотербеліс параметрлері және олардың шығу себептерін анықтау үшін Н. М. Крылов және Н. Н. Боголюбов жуықтау арқылы гармоникалық баланс әдісін өңдеп шығарды. Л. С. Гольдфарб жиілік және амплитуданың бірінші жуықтау кезінде жиіліктік сипаттама көмегімен автотербелістің негізгі гармоникасының графоаналитикалық әдісін берді. Осы әдістің кейінгі түрлендірулері Попов жұмыстарында табылды.

Автоматты реттеу теориясының соғыстан кейінгі жылдары дамуы өте қарқынды және өте жақсы нәтижелі болып табылады. Теорияның жаңа бөлімдерінің негіздері және басқарудың фундаментальді принциптері жайлы қысқаша айтып тоқталайық.

Г. В. Щипанов, В. С. Кулебакин, Б. Н. Петров еңбектері арқылы автоматты реттеу теориясын ауытқу бойынша, ауытқу компенсациясы теориясы және инварианттылығы жайлы өңделген.

В. В. Казакевич, А. А. Фельдбаум, А. А. Красовский және басқаларымен экстрималды басқару принциптері және экстримумды табу теориясы өңделді. Л. С. Понтрягин, А. М. Летов, Н. Н. Красовский және басқалары қолайлы басқару теориясы негізін жасады. Экстрималды қолайлы жүйелер теориясын өңдеу, онда қарастырылатын басқару түрлері тек қана реттеумен шектелмейтіндіктен, «Автоматты басқару және реттеу теориясы» курсының атына кеңейту негізін берді.

Қазіргі уақытта Автоматты басқару теориясы мәні тек техникалық жүйелер шегінде ғана өсті. Динамикалық басқарылатын процесстер тірі организмдерден орын алады, яғни экономикалық және ұжымдық адам-машиналық жүйелерде. Бұндай жүйелерде басқару функциялары толығымен басқарылатын құрылғыға беріле алмайды. Жауапкершілікті шешімдерді қабылдау адамға жүктеледі. Операциялардың бір бөлігі автоматтандырылатын, ал қалған бөлігі адаммен орындалатын жүйелер «автоматтандырылған басқару жүйелері» деген атқа ие болды. Автоматтандырылған басқару жүйелері бірнеше деңгейлерден құрылады: технологиялық процесстерде (ТПАБЖ), кәсіпорындарда (КАБЖ) және басқа салаларда. Автоматты басқару жүйелерінде есептеуіш техникалары кеңінен қолданылады. Автоматты басқару жүйелерін құру принциптерін үйрену арнайы оқу курсының пәнімен жүргізіледі.

Автоматты басқару жүйелерінде автоматтандырылған және автоматтандырылмаған операциялар санының арасындағы арақатынас әртүрлі деңгейлерде бірдей емес. ТПАБЖ-ның төмен деңгейінде автоматты құрылғылар рөлінен динамика рөлі басымырақ. Жоғарғы деңгейлерінде динамика есебі жүйенің структурасының күрделену салдары және басқарылатын айнымалылар санының өсуі сияқты қиындайды. Қазіргі кезде басқару динамикасының жаңа бөлімдері жіті дамуда: «Күрделі жүйелер динамикасы» сипаттамасы математикалық тілде орындала алатын күрделі

структуралы жоғары мөлшерлікті жүйелерді зерттейді және «Жүйелік динамика» формализмделінетін және формализмделінбейтін факторлар бар кезінде күрделі жүйелерді жүргізуді зерттейді. Жүйелік динамикада зерттеудің негізгі әдістерінің бірі иммитационды модельдеу болып табылады. Қазіргі кезде күрделі жүйелердің динамикасын және жүйелік динамиканы зерттеу өте кең таралған.

Күрделі жүйелерде динамика заңы негізгі және өзін басқаруды анықтау болып табылмайды, бірақ олардың әсері көбінесе болады және олардың есебінен бас тарту көп жоғалтуларға әкеліп соғады.

1Алгебралық критерийлері бойынша тұйық жүйенің тұрақтылығын зерттеу

1. 1 Гурвиц тұрақтылық критерийі

1895 жылы неміс математигі А. Гурвиц жүйе теңдігінің сипаттамалық коэффициенттерінен тұратын, анықтауыш формасында алгебралық тұрақтылық критериін жасап шығарды.

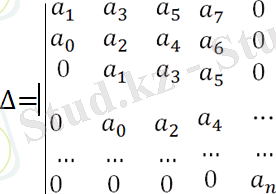Алдымен сипаттамалық теңдеудің коэффициентерінен келесі ережелермен Гурвицтің бас анықтауышын құрады:

(1. 1. 1)

анықтауыштың бас диогналінен солдан оңға қарай сипаттамалық теңдеудің барлық элементтерін $а_{1}$ -ден $а_{n}$ -гедейінгі барлық коэффициенттерді индекстерінің өсу ретімен теріп жазады. Бас диогнальдан жоғарғы бағандарды сипаттамалық теңдеудің тізбектің индекстерінің өсу ретімен орналастырса, төменгі бағандарды тізбектің индекстерінің кему ретімен орналастырады. Индекстері n -нен үлкен нольден кіші коэффициенттердің орнына ноль қойылады.

Пунктирде көрсетілгендей Гурвицтың бас анықтауышындағы диогнальды минорларды сызып тастап, Гурвицтың төменгі реттік анықтауышын аламыз:

$\mathrm{\Delta}_{1} = а_{1}$ ; $\mathrm{\Delta}_{2} = \begin{matrix} a_{1} & a_{3} \\ a_{0} & a_{2} \end{matrix}$ ; $\mathrm{\Delta}_{3} = \begin{matrix} a_{1} & a_{3} & a_{5} \\ a_{0} & a_{2} & a_{4} \\ 0 & a_{1} & a_{3} \end{matrix}$ ;

(1. 1. 2)

Гурвицтың анықтауышының номерін диогналі бойынша

коэффициенттердің нөмірімен анықтайды. Гурвиц тұрақтылық критериі келесідей құрылады: автоматты басқару жүйесі тұрақты болу үшін, Гурвицтың барлықанықтауыштары сипаттамалық теңдеудің бірінші коэффициентінің $а_{0}$ таңбасымен бірдей болу қажет және жеткілікті, яғни $а_{0}$ >0.

Осылайша, $а_{0}$ >0 болғанда жүйе тұрақтылығы үшін келесі шарттарды орындау қажет және жеткілікті:

$\mathrm{\Delta}_{1} = а_{1} > 0; {\ \ \mathrm{\Delta}}_{2} = \begin{matrix} a_{1} & a_{3} \\ a_{0} & a_{2} \end{matrix} > 0$ ; ${\ \ \ \mathrm{\Delta}}_{3} = \begin{matrix} a_{1} & a_{3} & a_{5} \\ a_{0} & a_{2} & a_{4} \\ 0 & a_{1} & a_{3} \end{matrix} > 0;$

. .

(1. 1. 3)

Гурвицтың анықтауыштары үшін бірінші, екінші, үшінші және төртінші сипаттамалық теңдеулерін ашсақ, келесі тұрақтылық шарттарын аламыз:

1. (n=1), a0s+a1s+a2=0a_{0}s + a_{1}s + a_{2} = 0, тұрақтылық шарты

$a_{0} > 0; \ a_{1} > 0;$ (1. 1. 4)

2. (n=2), a0s2+a1s+a2=0a_{0}s^{2} + a_{1}s + a_{2} = 0, тұрақтылық шарты

$a_{0} > 0; \ a_{1} > 0\ \ a_{2} > 0;$ (1. 1. 5)

3. (n=3), a0s3+a1s2+a2s+a3=0a_{0}s^{3} + a_{1}s^{2} + a_{2}s + a_{3} = 0, тұрақтылық шарты

$a_{0} > 0; \ a_{1} > 0\ \ a_{2} > 0; \ a_{3} > 0; \ a_{1}a_{2} - a_{0}a_{3} > 0; \$ (1. 1. 6)

4. (n=4), a0s4+a1s3+a2s2+a3s+a4=0a_{0}s^{4} + a_{1}s^{3} + a_{2}s^{2} + a_{3}s + a_{4} = 0, тұрақтылықшарты

$a_{0} > 0; \ a_{1} > 0\ \ a_{2} > 0; \ a_{3} > 0; \ a_{4} > 0$ ; (1. 1. 7)

${\ \ \ (a}_{1}a_{2} - a_{0}a_{3}) - a_{1}^{2}a_{4} > 0;$ (1. 1. 8)

Осылайша, бірінші және екінші ретті жүйе үшін қажетті және жеткілікті шарт, сипаттамалық теңдеудің коэффициенттерінің оң болуы. Үшінші және төртінші ретті теңдіктер үшін коэффициенттердің оң болуымен қатар теңсіздіктер де оң болуы қажет (1. 7), (1. 8) .

Гурвиц анықтауышының соңғы бағанында нольден алшақ коэффициент $a_{n\ }$ , сондықтан

$\mathrm{\Delta}_{n} = a_{n}\mathrm{\Delta}_{n - 1}$ (1. 1. 9)

Бұл теңдіктен $a_{n} > 0$ болған жағдайда жүйенің тұрақтылығын анықтау үшін $\mathrm{\Delta}_{1}$ -ден $\mathrm{\Delta}_{n - 1}$ -а дейінгі Гурвиц анықтауышын анықтаса жеткілікті. Гурвицтың төменгі реттік анықтауыштары оң, бас анықтауыш нольге тең болғанда жүйе тұрақтылық шекарасында болады:

$\mathrm{\Delta}_{n} = a_{n}\mathrm{\Delta}_{n - 1}$ (1. 1. 10)

Гурвиц критериін Раус критериінен де алуағ болады, сондықтан оны кейде Раус-Гурвиц критериі деп те атайды.

№ 9 нұсқа бойынша есептеу жүргізу.

Бастапқы берілгендер :

1. 1. 1-кесте

$$W(s) = \frac{0. 2 + 0. 3}{0. 93 + 0. 5s^{2} + 0. 9s + 0. 4};$$

$$D(s) = 0. 3s^{3} + 0. 5s^{2} + 0. 9s + 0. 9$$

$$\mathrm{\Delta} = \begin{Bmatrix} a_{1} & a_{3} & 0 \\ a_{0} & a_{2} & 0 \\ 0 & a_{1} & a_{3} \end{Bmatrix} = \begin{Bmatrix} 0. 5 & 0. 9 & 0 \\ 0. 3 & 0. 9 & 0 \\ 0 & 0. 5 & 0. 9 \end{Bmatrix};$$

$$\mathrm{\Delta}1 = 0. 5$$

$$\mathrm{\Delta}2 = \begin{Bmatrix} 0. 5 & 0. 9 \\ 0. 3 & 0. 9 \end{Bmatrix} = 0. 45 - 0. 27 = 0. 18$$

$\mathrm{\Delta}3 = \begin{Bmatrix} 0. 5 & 0. 9 & 0 \\ 0. 3 & 0. 9 & 0 \\ 0 & 0. 5 & 0. 9 \end{Bmatrix}$ =0. 162

$$\mathrm{\Delta}2 > 0; \mathrm{\Delta}3 > 0;$$

$$a_{0} = 0. 6 > 0; a_{1} = 0. 3 > 0; a_{2} = 0. 5 > 0;$$

$$\mathrm{\Delta}1 = 0. 5 > 0; \mathrm{\Delta}2 = 0. 18 > 0; \mathrm{\Delta}3 = 0. 162 > 0;$$

Тұрақтылық критерийі

Гурвиц тұрақтылық критерийі :Автоматты басқару жұйесі тұрақты болу үшін барлық матрицалардың шамалары оң болып және $а_{0}$ >0;

1. 2 Раустың орнықтылығының белгiсi .

1877 жылдағы бұл орнықтылықтың белгiсiнағылшын математигi Э. Раус ұсынылған, кейбiр ереже түрінде1. 1 -кестеде өте қарапайым ғана түсiндiрілетін алгоритм.

1. 1-кестесіндегі бiрiншi жолды мінездемелік теңдеуінде жұп индекстерді индекстердiң коэффициенттерiн өсу ретiмен жазады: а _0, а _2, а _4, а ₆ , . . . ; екiншi жолда тақ индекспен берілген коэффициенттер берілген: а _1, а _3, а _5, а ₇ , . . .

:

c _{k, i} =с _{k+1, i-2} - r _i c _{k+1, i-1,} (1. 2. 1)

мұндағы

r _i =c _{1, i-2} /c _{1, i-1.} (1. 2. 2)

(2. 1) және (2. 2) кестелеріндегі 1. 1 - кестенiң бағанының нөмiрін бiлдіретiн k индексі - 1. 1-кестенiң жолының нөмiрін бiлдiретiн і индекс.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс