Асқын өткізгіштік және кристалдық құрылым: Бравэ торлары, Бриллюэн зоналары және трансляциялық симметрия


Қазақстан Республикасының Білім және Ғылым министірлігі
Семей қаласындағы Шәкәрім атындағы Мемлекеттік университеті
СӨОЖ
Пән: Конденсацияланған күй физикасы
Тақырыбы: Асқын өткізгіштік. Бравэ торлары. Бриллюэн зоналары. Кристалдың трансляциялық симметриясы. Элементар ұяшық. Негізгі векторлар.
Орындаған : Айтқалиев Ж. Қ.
Топ: ТФ-319
Тексерген: Сейсенбаева М. Қ.
Семей 2015
Мазмұны:
1 Асқын өткізгіштік3
2 Бравэ торлары3
3 Бриллюэн зоналары5
4 Кристалдың трансляциялық симметриясы. Элементар ұяшық. Негізгі векторлар7
1 Асқын өткізгіштікАсқын өткізгіштік - кейбір өткізгіштерді белгілі бір алмағайып температураға (Та) дейін суыту кезінде олардың электрлік кедергісінің секірмелі түрде кенет нөлге дейін төмендеу құбылысы. Сынаптың темп-расын Т = 4, 15 К-ге төмендеткен кезде бұл құбылысты алғаш рет (1911) голланд физигі Х. Каммерлинг-Оннес байқаған. Ол кейін Т1Та темп-ра кезінде күшті магнит өрісінде (НТНа) сынаптың электрлік кедергісінің қалпына келетіндігін де анықтаған (мұндағы На - алмағайып магнит өрісінің кернеулігі) . Егер ТтТа және НТНа болса, онда асқын өткізгіш үлгінің қасиеті идеал диамагнеттің қасиетіндей болып өзгереді (қ. Диамагнеттік) . Сөйтіп, асқын өткізгіштің ішкі магнит индукциясы (В) 0-ге тең болады, яғни сыртқы магнит өрісі асқын өткізгіш ішіне өте алмайды. Бұл құбылыс Мейснер эффектісі деп аталады.
1967 жылы Дж. Бардин, Л. Купер, Дж. Шриффер (АҚШ) және Н. Н. Боголюбов (Ресей) Асқын өткізгіштіктің микроскопиялық теориясын жасады. Бұл теорияның негізіне спиндерінің таңбасы қарама-қарсы электрондар жұбы (Купер жұбы) алынған. Мұндай жұптың заряды 2 l-ге (мұндағы l - электрон заряды), спинінің мәні нөлге тең болады, әрі ол Бозе-Эйнштейн статистикасына бағынады. Асқын өткізгіштік құбылысы байқалатын металдарда жұптар бозе-конденсация құбылысына ұшырайды. Сондықтан купер жұптарының асқын аққыштық қасиеті болады. Сонымен Асқын өткізгіштік электрондық сұйықтықтың асқын аққыштығы болып табылады. Асқын өткізгіштік практикада кеңінен пайдаланылады. 20 ғасырдың соңында керамикалық материалдардың жоғары температурадағы (77-100 К) асқын өткізгіштігін зерттеу бағыты қарқынды дамуда. Ал Қазақстанда Асқын өткізгіштікті зерттеу ҚР ғылым академиясының Ядр. физ. ин-тында (ҚР ғылым академиясының корр. мүшесі Ә. Қ. Жетбаевтың жетекшілігімен) жүргізілуде.
2 Бравэ торлары
Геометрия тұрғысынан алғанда кристалдағы бөлшектердің периодты түрде қайталанып орналасуын параллель көшіру немесе трансляция операциясы көмегімен сипаттауға болады. 2 - суретте үш ось бойында параллель көшірген кезде пайда болған кристалдық тор көрсетілген: ОХ осі бойында
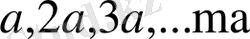 , ОУ осі бойында
, ОУ осі бойында
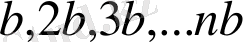 , ОZ осі бойында
, ОZ осі бойында
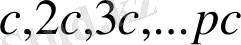 кесінділері (
кесінділері (
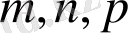 - бүтін сандар) . Осы тордағы кез- келген бөлшектің орны мына вектормен анықталады:
- бүтін сандар) . Осы тордағы кез- келген бөлшектің орны мына вектормен анықталады:
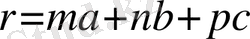
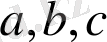 - векторлары ең қысқа трансляция векторлары, ал олардың шамалары - трансляция периодтары деп аталады.
- векторлары ең қысқа трансляция векторлары, ал олардың шамалары - трансляция периодтары деп аталады.
Қандай да, бір түйінді үш бағыт бойынша параллель көшіру арқылы алынған тор трансляциялық тор немесе Бравэ торы деп аталады.
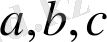 - векторларымен тұрғызылған ең кішкене параллелепипед кристалдың элементар ұяшығы деп аталады (сурет 1, б) . Торды құрайтын барлық элементар ұяшықтардың өлшемдері мен көлемдері бірдей. Ұяшықтардың төбелерінде бірдей атомдар немесе атомдар тобы орналасады. Сондықтан, ұяшықтардың барлық төбелері бір-бірімен эквивалентті. Оларды тор түйіндері деп атайды. Элементар ұяшықтарды сипаттау үшін жалпы жағдайда алты шама: ұяшықтың үш қабырғасы (
- векторларымен тұрғызылған ең кішкене параллелепипед кристалдың элементар ұяшығы деп аталады (сурет 1, б) . Торды құрайтын барлық элементар ұяшықтардың өлшемдері мен көлемдері бірдей. Ұяшықтардың төбелерінде бірдей атомдар немесе атомдар тобы орналасады. Сондықтан, ұяшықтардың барлық төбелері бір-бірімен эквивалентті. Оларды тор түйіндері деп атайды. Элементар ұяшықтарды сипаттау үшін жалпы жағдайда алты шама: ұяшықтың үш қабырғасы (
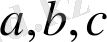 ) және олардың арасындағы үш бұрышты
) және олардың арасындағы үш бұрышты
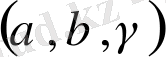 алу қажет. Бұлар элементар ұяшық параметрлері. Көбінесе торларда бірлік ұзындықты сипаттау үшін метр емес,
алу қажет. Бұлар элементар ұяшық параметрлері. Көбінесе торларда бірлік ұзындықты сипаттау үшін метр емес,
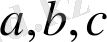 кесінділері қолданылады. Оларды осьтік бірліктер деп атайды.
кесінділері қолданылады. Оларды осьтік бірліктер деп атайды.
Түйіндерінде ғана бөлшектер орналасқан элементар ұяшықтар қарапайым немесе примитивті деп аталады. Ұяшықтың әрбір нүктесіне бір бөлшектен келеді.
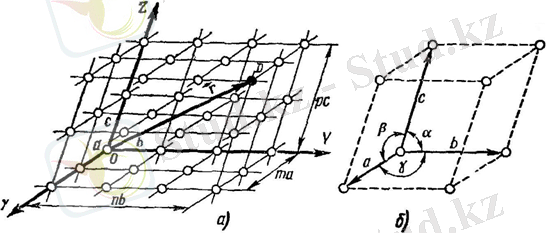
Сурет 1
Тор симметриясын толығымен өрнектеу үшін элементар ұяшықтарды тұрғызғанда бөлшектер тек қана түйіндерде ғана емес, сонымен бірге басқа нүктелерде де орналасқан деп алады. Бұлар күрделі ұяшықтар деп аталады. Олардың ішінде ең көп таралғандары (сурет 2) : көлемді центрленген (КЦ), қырлы центрленген (ҚЦ) және базалы центрленген (БЦ) .
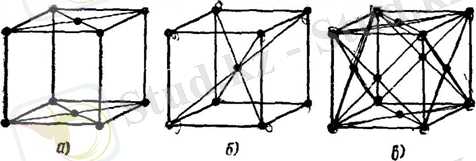
Сурет 2
Бұл ұяшықтарды қарапайым ұяшықтарға келтіру оңай, сондықтан осындай ұяшықтары бар торлар - Бравэ торлары деп аталады.
3 Бриллюэн зоналарыБриллюэн зоналары келесі түрде құрылады: кері торда түйіндерді қосатын кесінділердің ортасына нүкте қойылады. Бірінші зона - [- π / a , π / a ] кесіндісі, екіншісі - бірінші зонаны алып тастандағы [-2 π / a , 2 π / a ] кесіндісі, және т. с. с.
Сурет 3-те екіөлшемді тікбұрышты кері тор үшін Бриллюэннің төрт зонасы бейнеленген. Олар бірөлшемді жағдайдағыдай құрылады, тек нүктелердің орнына түзу сызықтар жүргізіледі.
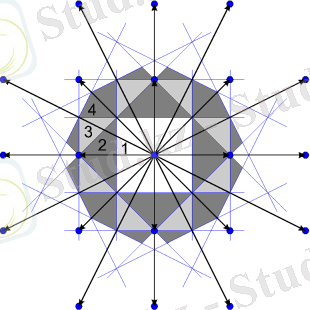
Сурет 3
Үшөлшемді тор үшін Бриллюэн зонасы ослай құрылады тек түзулердің орнына жазықтықтар жүргізіледі. Осылай анықталған жазықтықтар класы, координаталар басымен қосылған кері тордың түйіндерінің жан-жағын көпжақты пішіні бар қандай да бір көлеммен шектейді. Қарапайым кубты тор жағдайында көпжақты куб болып табылады. Оның қырлары осы тордың түйіндерін басқа көрші түйіндерімен қосатын векторлардың ортасы арқылы өткізілетін жазықтармен құрылған. Барлық басқа жазықтар түйіннен алшақ өтеді және кубтың қырларының құрылуына өз үлесін қоспайды. Көлемді-центрленген кубты тор жағдайында күрделі көпжақтылар құрылады (төменді қара) . Оның қырлары берілген түйін мен оның жақын бірінші және екінші көршілері арасынан өткізілген жазықтармен құрылады. Құрылған көпжақтылар Бриллюэннің бірінші зонасы деп аталады. Егер барлық жазықтардың бірігуінен Бриллюэннің бірінші зонасының қырларын алып тастасақ, онда қалған көптік координата басы айналасында жаңа көпжақтының құрылуын шектейді. Бриллюеннің бірінші зонасына кірмейтін осы көптіктің жартысы Бриллюэннің екінші зонасын түзеді. Келесі қадамда біз Бриллюэннің үшінші зонасын аламыз және т. с. с.
Бриллюэннің бірінші зонасын нүктелік симметриясы бар, кері тордың примитивті ұяшығы ретінде қарастыруға болады. Расында да, егер кері тордың әр түйінінің жанына Бриллюэннің бірінші зонасын құрсақ (координаталар басын осы түйінге орналастырсақ), онда осы зоналар бір-бірімен беттеспей барлық кеңістікті толығымен толтырады. Мұнда Бриллюэннің бірінші зонасының көлемі кері тордың примитивті ұяшығының көлеміне тең болатындығын көруге болады.
Бриллюэннің кейбір қасиеттері:
Бриллюэннің барлық зоналарының көлемдері бірдей және кері тордың примитивті ұяшығының көлеміне тең.
Бриллюэннің барлық зоналары бірінші зонаның репликасы болып табылады: оларды бірінші зонаға жататын нүктелерін кері тор векторына трансляциялау арқылы алуға болады.
кең таралған түрлерінің көпшілігінің торлары қырға центрленген кубты (ГЦК) Браве торларына жатады, осы тордың Бриллюэннің бірінші зонасы қалай орналасқанын қарастырайық. Мұндай жағдайда кері тор көлемді центрлі кубты (КЦК) болып табылады. Бриллюэннің бірінші зонасы сурет 4-те бейнеленген. Жоғарыда көрсетілген алгоритмге сәйкес ол келесідей болады. Бірінші кубты, қарапайым ұяшықтың центріндегі түйін мен оның екінші көршісінің арасын қосатын түзуді екіге бөлетін жазықтық жүргіземіз. Бұл жазықтықтар кубты ұяшықтармен сәйкес келетін, орталық түйіннің жан жағындағы кубты шектейді. Осы кубтың бұрыштарында орталық түйіннің жақын көршілері орналасқан. Осы көршілері мен орталық түйіндері арасынан жүргізілетін жазықтықтар кубпен қиылысқан кезде алтыбұрышты қырларды түзеді, ал кубтың қырларынан квадраттарды ''қиып '' алады.
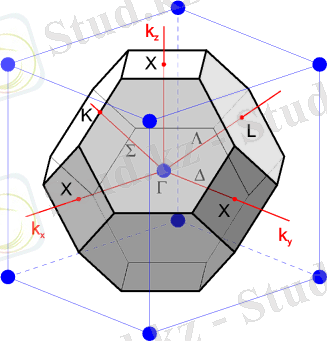
Сурет 4
ГЦК-торда Бриллюэннің бірінші зонасының кейбір жоғары симметриялы нүктелері мен сызықтарының жалпыға бірдей белгіленулері бар. Бриллюэн зонасының центрі грек әрпімен белгіленеді Γ . Жазықтық бетіндегі нүктелер латын әріптерімен белгіленеді: X - квадрат қырының центрі ( k -жазықтығындағы (1, 0, 0) бағыты және оған эквивалент барлығы 6 нүкте) ; L - алтыбұрышты қырдың центрі ((1, 1, 1) бағыты және оған эквивалент барлығы 8 нүкте) ; K - көрші алтыбұрышты қырлардың арасындағы қабырғалардың ортасы ((1, 1, 0) бағыты және оған эквивалент барлығы 12 нүкте) . Зона центрі мен жазықтық бетіндегі нүктелерді қосатын сызықтар грек әріптерімен белгіленеді: Γ X - Δ ((1, 0, 0) түріндегі бағыт), ΓL - Λ ((1, 1, 1) түріндегі бағыт), Γ K - Σ ((1, 1, 0) түріндегі бағыт) .
4 Кристалдың трансляциялық симметриясы. Элементар ұяшық. Негізгі векторларҚатты дене физикасының тарихындағы маңызды кезең Макс фон Лауэ рентген сәулесінің дифракциясы арқылы кристалл атомдардың периодты қатарынан тұратындығын дәлелдеген 1912 жыл болып саналады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz