Динамикалық хаос теориясы негізінде радиосәулелену импульстерінің ақпараттық-энтропиялық және мультифракталдық сипаттамасы


ӘЛ- ФАРАБИ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ УНИВЕРСИТЕТІ
ФИЗИКА ФАКУЛЬТЕТІ
ЭЛЕКТРОНИКА ЖӘНЕ БЕЙСЫЗЫҚ ТОЛҚЫНДЫҚ ПРОЦЕСТЕР КАФЕДРАСЫ
БІТІРУ ЖҰМЫСЫ
КЕЙБІР АСТРОФИЗИКАЛЫҚ ҚҰБЫЛЫСТАРДЫ ДИНАМИКАЛЫҚ ХАОС ТЕОРИЯСЫ ӘДІСІМЕН СИПАТТАУ
Орындаған:
4- курс студенті . . . Т. Ахатұлы
(қолы, күні)
Ғылыми жетекші:
ф. -м. ғ. к ., аға оқытушы . . . Н. Т. Ізтілеуов
(қолы, күні)
Қорғауға жіберілді:
кафедра меңгерушісі,
ф. -м. ғ. д., профессор . . . З. Ж. Жаңабаев
(қолы, күні)
Алматы-2008 ж.
Реферат
беттер саны 34
суреттер саны 20
қолданылған әдебиеттер саны 15
қосымшалар саны 1
Кілтті сөздер: ДИНАМИКАЛЫҚ ХАОС, энтропия, ИНФОРМАЦИЯ, фрактал, мультифрактал, аффинділік КОЭФФИЦИЕНТІ, РАДИОСӘЛЕЛЕНУ, жалпыландырылған метрикалық сипаттама, мультифракталДЫҚ СПЕКТР, ФАЗАЛЫҚ СУРЕТ.
Берілген бітіру жұмыстың мақсаты бейсызық физика әдістерін пайдаланып радиосәулелену ағынын зерттеп, сипаттау болып табылады. Жұмыста радиосәулелену импульстерінің информациялық-энтропиялық және мультифракталдық сипаттамалары зерттелді.
Мультифракталдық өлшемділіктің, сигналдардың энтропиясы және жалпыландырылған метрикалық сипаттамалары келтірілген, мультифракталдық спектрлер көрсетілген.
МАЗМҰНЫ
РЕФЕРАТ . . . 2
КІРІСПЕ . . . 3
НЕГІЗГІ БӨЛІМ
1. ТАРАУ. Бейсызық физиканың негізгі әдістері . . . 5
1. 1. Динамикалық хаос теориясы әдісі . . . . . . ……. … . . . 5
1. 2. Информациялы-энтропиялы талдау әдісі . . . 10
1. 3. Фракталдық және мультифракталдық әдістер . . . 15
2. ТАРАУ. НАҚТЫ АСТРОФИЗИКАЛЫҚ ҚҰБЫЛЫСТЫ БЕЙСЫЗЫҚ ТАЛДАУ . . . 19
2. 1. Сигналдардың мультифракталдық талдауы……… . . . . . . 19
2. 2. Сигналдардың информациялық- энтропиялық талдауы . . . 25
2. 3. Зерттеу нәтижелері . . . 27
Қорытынды . . . 31
Қолданылған әдебиеттер тізімі . . . 32
1 Қосымша . . . 33
КІРІСПЕ
Астрофизикалық құбылыстарды бейсызық физикасы әдістерін қолданып түсіндіру қазіргі кезде өте үлкен қызығушылық туғызуда. “Соңғы кездері электромагниттік және корпускулалық сәулеленудің зерттеулері өте кең диапазонында жүргізіледі. Өткен ғасырдың басында А. Л. Чижевский орнатқан Жер құбылыстары мен Күнде болатын үдерістердің байланысын және Күн белсенділігінің периодтылығын қазіргі кезде жаңа ғылыми бағыт түрінде космостық ауа райында қолдауын тапты [1] .
Күн белсенділігінің әртүрлі көріністерінің ішінен өте үлкен қызығушылық туғызатыны бейстационарлы Күн құбылыстары, ол дербес жағдайда, Күннің жарқ етуі. Соңғы он жыл ішінде Күннің жарқ етуін зерттеуге арналған, ерекшелігінде ірі жарқылды оқиғаларды зерттеуге арналған, яғни
 эрг-қа дейін ортақ энергия шығаратын оқиғаларға арналған өте көп жұмыстар басылып шықты. Бұл біріншіден, осы құбылыстардың Жер маңындағы космостық кеңістікке үлкен әсерімен, екіншіден, кейбір ірі жарқыл сипаттамаларын өте аз балды жарқ етулерімен салыстыру арқылы оңай анықтауға болады. Бірақ, техникалық базаның дамуынан, жарқ ету туралы эксперименталды материалдардың жинағынан және Күн белсенділігі механизімі туралы теориялық көріністердің дамуынан аз қуатты жарқ ету оқиғаларын тереңірек зерттеу мүмкіндігі болды. Бұл жолда Күннің жарқ етуі физикасының өзінде де және кейбір өте маңызды аралас мәселелерде жаңа нәтижелерді күтуге болады, мысалы Күн тәжінің қызып кету мәселесі. Сондай-ақ, ірі жарқ ету талдауында көбінесе қарастырып отырған құбылыстардың күрделілігімен қиындатылған, мұндай жарқ етулерде плазма- магниттік құрылымдардың әртүрлі бөліктерінде және жарқыл дамуының әртүрлі этаптарында жарқ ету үдерісінің өзара қабаттасуы өтеді. Шындығында, берілген зонадағы жарқ ету энергия шығарудың жекелеген этаптарын айқын бөліп алу өте қиын болғанда, нақты зерттелетін жағдайларда біз көптеген құбылыстардың суперпозициясын бақылаймыз. Тіпті орташа қуатты жағдайларда жекелеген өте ұсақ жарқ ету құбылыстарының өзіндік «ретсіздігі» бақыланады. Сондықтан бізге кем дегенде қарапайым жарқ ету этаптарының нақты кеңістіктік және уақыттық локализация энергияның қарапайым бөлінуіне қатысты нақты бөліп алу кезіндегі талдаулары өте маңызды. Нақтысында, жекелеген минималды жарқ етуді бөліп алып (минималды энергия шығарумен) және оның даму этаптарын қадағалау [1] . Осының бәрі осы жұмыстың мақсатын айқындап берді: динамикалық хаос сипатамаларын пайдаланып радиосәулелену ағынының физикасын ашу, сапалы түрде сипаттап беру.
эрг-қа дейін ортақ энергия шығаратын оқиғаларға арналған өте көп жұмыстар басылып шықты. Бұл біріншіден, осы құбылыстардың Жер маңындағы космостық кеңістікке үлкен әсерімен, екіншіден, кейбір ірі жарқыл сипаттамаларын өте аз балды жарқ етулерімен салыстыру арқылы оңай анықтауға болады. Бірақ, техникалық базаның дамуынан, жарқ ету туралы эксперименталды материалдардың жинағынан және Күн белсенділігі механизімі туралы теориялық көріністердің дамуынан аз қуатты жарқ ету оқиғаларын тереңірек зерттеу мүмкіндігі болды. Бұл жолда Күннің жарқ етуі физикасының өзінде де және кейбір өте маңызды аралас мәселелерде жаңа нәтижелерді күтуге болады, мысалы Күн тәжінің қызып кету мәселесі. Сондай-ақ, ірі жарқ ету талдауында көбінесе қарастырып отырған құбылыстардың күрделілігімен қиындатылған, мұндай жарқ етулерде плазма- магниттік құрылымдардың әртүрлі бөліктерінде және жарқыл дамуының әртүрлі этаптарында жарқ ету үдерісінің өзара қабаттасуы өтеді. Шындығында, берілген зонадағы жарқ ету энергия шығарудың жекелеген этаптарын айқын бөліп алу өте қиын болғанда, нақты зерттелетін жағдайларда біз көптеген құбылыстардың суперпозициясын бақылаймыз. Тіпті орташа қуатты жағдайларда жекелеген өте ұсақ жарқ ету құбылыстарының өзіндік «ретсіздігі» бақыланады. Сондықтан бізге кем дегенде қарапайым жарқ ету этаптарының нақты кеңістіктік және уақыттық локализация энергияның қарапайым бөлінуіне қатысты нақты бөліп алу кезіндегі талдаулары өте маңызды. Нақтысында, жекелеген минималды жарқ етуді бөліп алып (минималды энергия шығарумен) және оның даму этаптарын қадағалау [1] . Осының бәрі осы жұмыстың мақсатын айқындап берді: динамикалық хаос сипатамаларын пайдаланып радиосәулелену ағынының физикасын ашу, сапалы түрде сипаттап беру.
1 ТАРАУ
1. 1 Динамикалық хаос теориясы әдісінің сипаттамалары
Динамикалық жүйелер ұғымы Ньютонның дифференциалдық теңдеулерімен сипатталатын механикалық жүйенің жалпыланған ұғымы түрінде пайда болды. Ол табиғаттың қай жүйесі болмасын: физикалық, химиялық, биологиялық, экономикалық т. б. қамтиды және тек детерминдік жүйелер ғана емес, стохастикалық жағдайларды да қарастырады. Динамикалық жүйені сипаттау әдістері әртүрлі. Олар -дифференциалдық теңдеулер, логикалық алгебра функциясы, графтар, марковтық тізбектер және т. б амалдар.
Қазіргі уақытта динамикалық жүйені бейнелейтін математикалық модельдердің екі түрі қолданылады.
1-ші көзқарас бойынша
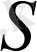 динамикалық жүйенің математикалық моделі қайсібір уақыт кезеңіндегі жүйенің
х
жағдайы қарастырылады және осы
х
жағдайдың уақыт бойынша өзгерісін анықтайтын
Т
операторы ұғымын пайдаланады.
Т
операторы келесі
динамикалық жүйенің математикалық моделі қайсібір уақыт кезеңіндегі жүйенің
х
жағдайы қарастырылады және осы
х
жағдайдың уақыт бойынша өзгерісін анықтайтын
Т
операторы ұғымын пайдаланады.
Т
операторы келесі
 уақыт кезеңінде жүйенің
уақыт кезеңінде жүйенің
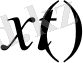 бейнелеуі бойынша
бейнелеуі бойынша
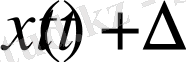 бейнелеуін орындау амалын көрсетеді. Егер
T
операторы уақытқа нақты тәуелді болмаса, онда
S
жүйесі
автономды
деп аталады, ал қарама-қарсы жағдайда - автономды емес.
S
жүйесінің
х
жағдайын Ф кеңістіктің біраз нүктесі ретінде, мысалы координаттармен, импульстармен, яғни
S
жүйесінің
фазалық кеңістігі
деп қарастыруға болады.
х
жағдайының өзгерісіне Ф фазалық кеңістіктегі
бейнелеуші
деп аталатын нүктелер қозғалысы жауап береді. Бейнеленген нүктелер қозғалысы
фазалық траектория
деп аталатын қисықты сипаттайды. Фазалық кеңістік Ф және оператор
T
динамикалық жүйенің математикалық моделін құрайды. Осындай әдіс динамикалық жүйелердің өзгерісін Ф фазалық кеңістіктің құрылымдық сипатын анықтау және осы құрылымының жүйенің физикалық параметрлерінің шамасына тәуелділігін анықтау арқылы сипаттайды.
бейнелеуін орындау амалын көрсетеді. Егер
T
операторы уақытқа нақты тәуелді болмаса, онда
S
жүйесі
автономды
деп аталады, ал қарама-қарсы жағдайда - автономды емес.
S
жүйесінің
х
жағдайын Ф кеңістіктің біраз нүктесі ретінде, мысалы координаттармен, импульстармен, яғни
S
жүйесінің
фазалық кеңістігі
деп қарастыруға болады.
х
жағдайының өзгерісіне Ф фазалық кеңістіктегі
бейнелеуші
деп аталатын нүктелер қозғалысы жауап береді. Бейнеленген нүктелер қозғалысы
фазалық траектория
деп аталатын қисықты сипаттайды. Фазалық кеңістік Ф және оператор
T
динамикалық жүйенің математикалық моделін құрайды. Осындай әдіс динамикалық жүйелердің өзгерісін Ф фазалық кеңістіктің құрылымдық сипатын анықтау және осы құрылымының жүйенің физикалық параметрлерінің шамасына тәуелділігін анықтау арқылы сипаттайды.
Физикалық жүйеде хаостың пайда болу критерийлері екі түрлі болады: болжамдық ережелер (хаостың тууын жорамалдайтын) және диагностикалық құралдар (хаостың не бар, не жоқ болуын анықтайтын) .
Хаосты тербелістерді болжау ережесі деп хаосты тудыратын басқарушы параметрлердің жиынтығын анықтайтын критерийді айтамыз. Физикалық жүйеде хаостың пайда болуын болжау жүйенің жуықталған математикалық моделі (одан критерий шығаруға болатын), немесе көптеген тәжірибелер жүзінде жинақталған мәлімет болуға байланысты. Хаостың туындайтынын болжайтын негізгі болжамдық модельге периодтың екі еселену критериі, гомоклиникалық траекторияның бар болу критериі мен консервативті хаостың резонанстарының бір-бірінмен қабаттасуы (Чириков критериі) сондай-ақ, алмасу және өтпелі критерийі жатады.
Хаостық тербелістердің диагностикалық критериі деп өлшеулер нәтижесінде немесе мәліметтерді өңдеу арқылы зерттелетін жүйе хаостық динамика күйінде болатындығын анықтайтын тесті атайды. Диагностикалық сипаттамалар: Ляпунов көрсеткіші және фракталдық өлшемділік. Фракталдық модельдің физикада қолдану жетістігі: көптеген процестер мен объектлердің фракталдық заңдылығының болуы.
Пуанкаре бейнесі
Динамикалық жүйелерге математикалық өңдеу жасағанда { х ( t 1 ) , х ( t 2 ), …, х ( t n ), …, х ( t N ) } мәліметтердің уақыттық іріктелуін бейне деп атайды, ол үшін мына белгілеу енгізілген: х n ≡ х ( t n ) . Қарапайым детерминдік бейнеде х n +1 шамасын х n мәні бойынша табуға болады. Бұны көбінде мынадай түрде жазады:
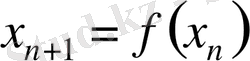 . (1)
. (1)
Бұндай жазылудан айырымдық теңдеуді тануға болады. Бейне ұғымы бұдан да көп айнымалыларға жалпыланады.
Мысалы, [
х
(
t
),
 (
t
) ] фазалық жазықтығында бейнеленген бөлшектің қозғалысын қарастырайық дейік. Егер қозғалыс хаосты болса, онда траектория фазалық кеңістікті толтыруға тырысады. Бірақ, егер біз қозғалысты үздіксіз бақыламай, динамикалық сипаттамаларын тек жеке кезеңдерде тіркесек, одна қозғалыс фазалық кеңістіктің нүктелер тізбегімен беріледі (1-сурет) . Егер
х
n
≡
х
(
t
n
) және
у
n
≡
(
t
) ] фазалық жазықтығында бейнеленген бөлшектің қозғалысын қарастырайық дейік. Егер қозғалыс хаосты болса, онда траектория фазалық кеңістікті толтыруға тырысады. Бірақ, егер біз қозғалысты үздіксіз бақыламай, динамикалық сипаттамаларын тек жеке кезеңдерде тіркесек, одна қозғалыс фазалық кеңістіктің нүктелер тізбегімен беріледі (1-сурет) . Егер
х
n
≡
х
(
t
n
) және
у
n
≡
 (
t
n
), онда фазалық кеңістіктің бұл нүктелер тізбегі екі өлшемді бейнені береді
(
t
n
), онда фазалық кеңістіктің бұл нүктелер тізбегі екі өлшемді бейнені береді
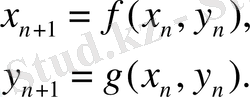 (1)
(1)
Егер t n іріктеу уақыты белгілі ережеге бағынса, бұл бейне Пуанкаре бейнесі деп аталады [1-5] .
Жеке бейсызық жүйелер үшін Пуанкаре бейнесін таза күйінде табу өте қиынға түседі (тек дифференциалдық теңдеуді аналитикалық жолмен шешкен жағдайларда мүмкін) . Біз Пуанкаре бейнесін логикалық теңдеу үшін тұрғызамыз.
Популяцияның өсуінің ең қарапайым моделі логикалық теңдеу болып табылады:
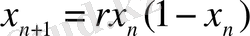 ,
,
 , (2)
, (2)
мұнда х n - физикалық өлшемнің байқалуы, r - басқарушы параметр. Төменде логикалық теңдеудің шешімін іске асыру, Пуанкаре программасы және сәйкес графиктер келтірілген (2, 3суреттер) . MatLab жүйесі арқылы алынған.
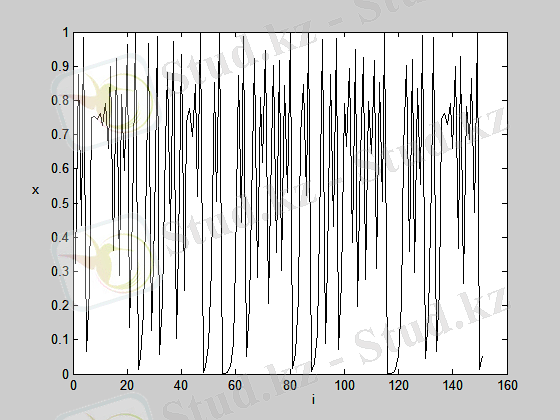
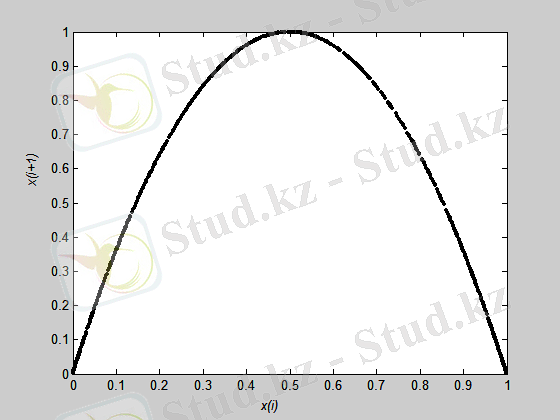
Бифуркациялық даграммалар
Математикалық түрде біраз маңызды физикалық есептер параметрлерге байланысты дифференциалдық теңдеулерге сәйкес келеді. Параметрлердің өзгерісі қозғалыстың бір режимінің орнықтылығының жоғалтып, жүйенің басқа күйге өтуіне әкелу мүмкін. Мысал - параметр генерация табалдырығынан асқанда Ван-дер-Поль генераторында жаңа периодты қозғалыстың пайда болуы. Бұл құбылыс бифуркация деп аталады, ал ол болған кездегі параметрдің мәні - бифуркация нүктесі. Ең қажет бифуркациялар - бифуркация нүктесінен өткенде жүйеде қозғалыстың жаңа орнықты режимдерінің пайда болуы.
Периодтың екі еселенуі арқылы хаосқа көшу . Периодтың екі еселену құбылысы байқалса кезде, бастапқы күйде жүйе негізгі периодты қозғалыста болады. Одан кейін тәжірибенің қандай-да r параметрін өзгерткенде бифуркация, немесе, периоды алғашқысынан 2 есе артатын периодты қозғалысқа ауысу байқалады. r параметірін әрі қарай өзгерткенде, жүйе тізбекті бифуркацияларға ұшырайды, әр бифуркация кезінде период екі еселенеді. Периодтың тізбекті екі еселенуі жүретін кезде r параметрінің “күдікті” мәні п → ∞ ұмтылғанда келесі автомодельді қатынасқа бағынады:
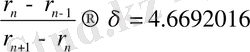 . (3)
. (3)
Бұл сан оны анықтаған адам құрметіне Фейгенбаум саны деп аталады. Іс жүзінде δ шамасы үшінші немесе төртінші бифуркацияда-ақ жинақталады. Периодтың еселену процесі белгілі бір параметрдің шекті мәнінде жиілеп, одан кейін хаосты қозғалысқа айналады.
Бифуркациялық диаграммалар. Логистикалық бейнелеудің бифуркациялық диаграммасын тұрғызу программасы және оның графигі (9-сурет) төменде келтірілген. 9-суретте келтірілген фазопараметрлік диаграмма хаосқа әкелетін периодтың екі еселену каскадты жүйесіне сәйкес. Диаграммалардың осындай түрі Фейгенбаум бұтағы деп аталады. Диаграмма динамикалық айнымалының масштабының бөлінуінің көрнекі мысалы, масштабтың скейлинг қасиеттерін көрсетеді, яғни көріністің бір элементі кішірек масштабта қайталана береді.
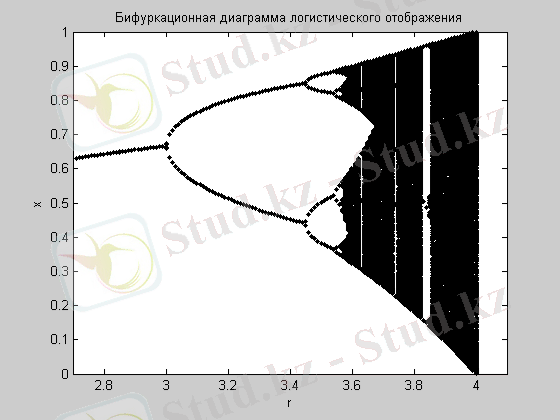
4-сурет. Логистикалық бейнелеудің бифуркациялық диаграммасы
Ляпунов көрсеткіштері
Детерминдік жүйелердегі хаос қозғалыстың бастапқы шарттардан сезімтал тәуелді екенін білдіреді. Яғни, фазалық кеңістікте алғашқы уақытта бір біріне жақын екі траектория аз уақыттың ішінде экспоненциалды ажырайды. Егер d 0 - берілген екі нүктенің арасындағы бастапқы ара қашықтықтың өлшемі болса, онда t аз уақыт ішінде осы нүктелерден шыққан траекториялар арасындағы ара қашықтық мынаған тең болады:
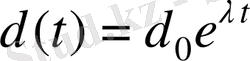 . (4)
. (4)
Егер жүйе айырымды теңдеулермен, немесе бейнелеумен сипатталса, онда
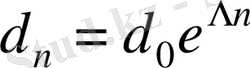 . (5)
. (5)
λ және Λ өлшемдері Ляпунов көрсеткіштері деп аталады.
Хаостық траекторияның экспоненциалды ажырауы аз аумақта ғана болуы мүмкін, өйткені егер жүйе шектелген болса (ал, көпшілік физикалық тәжірибелер шектелген жүйені сипаттайды), онда d ( t ) шексіз өсе бере алмайды. Сондықтан траекторияның ажырау мөлшерін анықтау үшін 13-суретте көрсетілгендей траектория бойындағы көптеген нүктелер бойынша экспоненциалды өсуін орташалау керек. Ляпунов көрсеткішін есептеу реперлі траекторияны (немесе тірек траектория) және көрші траекторияның нүктесін таңдап, d ( t ) / d 0 шамасын есептеуден басталады. d ( t ) ара қашықтығы тым үлкен болса (яғни экспоненциалды түрден оның өсі ауытқыса), зерттеуші жаңа «көрші» траекторияны тауып, қайтадан бастапқы d 0 ( t ) ара қашықтығын анықтайды [6, 7] . Ляпунов көрсеткішін былай табуға болады
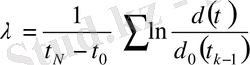 . (6)
. (6)
Ляпунов көрсеткіші термині бойынша хаостың критериі мына түрде жазылады:
λ > 0 - хаостық қозғалыс, (7)
λ ≤ 0 - регулярлы қозғалыс.
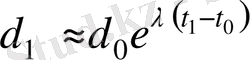
5-сурет. Ляпунов көрсеткішінің ең үлкен мәнін анықтауда қолданылатын екі көрші траекторияның арасындағы ара қашықтықтың өзгерісі
Бір өлшемді бейне үшін λ анықтайық:
х п+ 1 = f ( x n ) . (8)
f ( x ) функциясы тегіс әрі дифференциалданады, көрші траекториялар ара қашықтығы df / dx шамасымен өлшенеді. Бұған көз жеткізу үшін, бастапқы екі шарт енгіземіз: х 0 және х 0 + ε , онда (12) -қатынаста
d
0
=
 ,
,
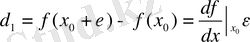 .
(9)
.
(9)
(13) -қатынас бойынша Ляпунов көрсеткішін (немесе сипаттық көрсеткішті) былай анықтаймыз
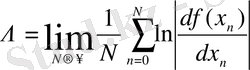 . (10)
. (10)
Ляпунов көрсеткішін есептеудің екі жалпы тәсілі бар: біреуі белгілі дифференциалдық жүйе немесе айырымды теңдеулерден алатын мәліметтер үшін, екіншісі - тәжірибелік уақыттық қатарлардың мәндері үшін.
1. 2 Сигналдарды информациялы-энтропиялық талдау
Нақтылы объектілер сыртқы ортамен энергиямен, затпен және информациямен алмаса алатын ашық жүйе болып табылады. Объектің тегіне тәуелсіз зерттелетін процес ықтималды құрылымда болса, оның симметриясы бұзылған кезде информация пайда болады. Екінші жағынан, табиғи құрылым - хаостан өз бетінше тәртіп орнау да - нақты бейсызық, ашық жүйелердің мейлінше жалпы даму заңдылығы. Информацияның және информациялық энтропияның физикалық аспектілерін қарастырайық.
Информация ұғымы. Информациялық энтропия
Жалпы қабылданған терминологияға сәйкес информацияның келесі анықтамаларын қолданамыз.
«Информация» ұғымы әртүрлі мағынаға ие. Қоғамдық-саяси информация әлеуметтік жүйенің өзекті жаңалықтары туралы мәліметтердің жиыны болып табылады. Кибернетикада информация ұғымы сигналдарды сақтау, өңдеу және жіберумен байланысты. Ықтималдықтар теориясында информация аддитивті мөлшерлік өлшем ретінде кездейсоқ оқиғаларды бір-біріне қатысты ықтималдылығымен салыстыру арқылы енгізіледі. Барлық информация теориясы негізінде информацияны мөлшерлі бағалау жатыр. Қарапайым комбинаторикалық формада бұл тұжырымды Р. Хартли ұсынды, ал толық аяқталған түрін К. Шеннон тұжырымдады.
Шеннон информация теориясы О және L екі таңбаның арасындағы (биттер арасындағы) қарапайым альтернативті таңдаудан шығады, ондағы L 1-ге, “иә”, “шындық” т. с. с. теңестірілсе, ал О 0-ге, “жоқ”, “жалған” теңестіріледі. Мұндай таңдау екі белгіден тұратын хабарды қабылдауға сәйкес келеді.
Мұндай хабарда болатын информация мөлшері бірлік ретінде қабылданады және ол бит деп аталады. Сондықтан бит - екілік белгі және информация мөлшерінің өлшем бірлігі, ол екі байланысқан тең ықтималдықты таңдамадағы информация мөлшері ретінде анықталады.
Айталық
 (11)
(11)
-
Х
және
Y
әріптерімен сәйкес белгіленген жүйенің күйін сипаттайтын айнымалылар жыйыны болсын. Егер
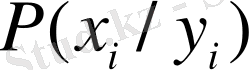 -
Х
жүйесі
-
Х
жүйесі
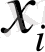 күйде болғанда
Y
у
i
күйіне өту ықтималдығы (шартты ықтималдық) болса, онда
Y
жүйесінің алған информациясы мынаған тең:
күйде болғанда
Y
у
i
күйіне өту ықтималдығы (шартты ықтималдық) болса, онда
Y
жүйесінің алған информациясы мынаған тең:
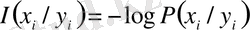 . (12)
. (12)
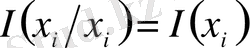 -
X
жүйесіндегі
-
X
жүйесіндегі
 оқиғасына қатысты
оқиғасына қатысты
 информация мөлшері деп аталады.
информация мөлшері деп аталады.
Ықтималдық
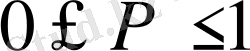 арасында жатқандықтан
I
әрқашан оң шама.
арасында жатқандықтан
I
әрқашан оң шама.
Логарифм негізін таңдауға байланысты информация мөлшері екілік, ондық және натурал логарифм бойынша: сәйкесінше бит , дит , нат - пен өлшенеді.
Статистикалық физикада энтропия ∆Г - жүйенің ішкі макроскопиялық күйінің статистикалық салмағының логарифмі ретінде енгізіледі:
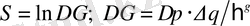 , (13)
, (13)
мұндағы ∆p⋅∆q- фазалық көлем, ћ -Планк тұрақтысы, g -жүйенің еркіндік дәрежесінің саны. Классикалық физикада ћ қолданбайтындықтан энтропияны нақты анықтауға болмайды. (5) -ші формуланың түрі күрделі жүйенің энтропиясының аддитивтік талаптарынан шығады:
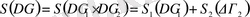 . (14)
. (14)
Идеал газдың энтропиясын (4) -ші формула бойынша есептей отырып (5) -ші формулаға келуге болады, мұндағы ∆Γ - идеал газдың қысымы, көлемі, температурасы бойынша анықталады.
Энтропия түсінігі сонымен қатар кездейсоқ шамалардың ықтималдықтарының таралуына да байланысты. Е i энергияның теңықтималдықты таралуы кезінде жүйенің ішкі таралу ықтималдылығы былай анықталады.
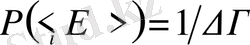 .
.
Энтропияны мына түрде табамыз
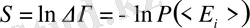 . (15)
. (15)
Орташа ықтималдықтың мағынасы бойынша (15) былай жазылады:
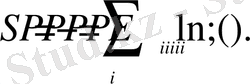 (16)
(16)
(8) - бойынша анықталған энтропия информациялық энтропия деп аталады [8, 9] . (2) және (8) өрнектерін салыстыру арқылы информациялық энтропия информацияның орташа ықтималдық мәнін анықтайтындығы көрінеді. Жүйенің теңықтималды таралуы кезінде жүйе туралы анықталмағандық максимумге жетеді, яғни жүйе туралы барлық информация жоғалып энтропияға айналады (7) . Тепе-тең жүйе информацияны сақтай алмайды. Информацияны білу анықталмағандықты азайтады. Сондықтан информация мөлшерін жоғалған анықталмағандық, яғни энтропия мөлшерімен өлшеуге болады:
I = S pr - S ps ,
мұнда pr - индекс «априорлы» дегенді білдіреді (тәжірибеге дейін) ps «апостериорлы» (тәжірибеден кейін) . Осы себептен әдебиеттерде (16) -ші өрнекпен анықталатын шама кейде информация деп аталады( егер ол қабылданса), кейде энтропия деп аталады (егер ол жоғалса) . Осылайша Х шамасы туралы информация Ү берілген кезде мына теңдікпен анықталады.
I ( X ) = S ( X ) - S ( X/Y ) .
(16) -ші өрнектен энтропияның қасиеттері шығады:
- алдын-ала белгілі хабардың энтропиясы 0 -ге тең.
- барлық басқа жағдайлардаS >0 болады.
Ашық жүйелердің өзқауымдық деңгейлерінің критерийлері
Жалпы қабылданған терминологияға сәйкес I i информациясы, P i ықтималдыққа ие құрылым пайда болғанда (жоғалғанда) (2) формуламен есептелінеді және келесі түрде табылады:
60
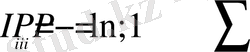 , (17)
, (17)
ал оның орта мәні - информациялық энтропия (8) -өрнекпен анықталады.
Әртүрлі иерархиялық деңгейлердегі өзұқсастық, өзқауымдық жүйелердің әмбебаптық қасиеттерінің бірі болып табылады. Олардың сипаттамасының масштабты инварианттылығы информацияның үздіксіз мәндерін қабылдауға мүмкіндік береді. Ал информацияны анықтаушы физикалық шама ретінде қабылдауға болады. Мұндай жағдайлар, алдымен күй функцияларының арасында (мысалы энергия мен энтропияның арасында) бірмәнді емес байланыс орнайтын күшті бейсызық динамикалы-информациялық жүйелерге (турбулентті орта, биологиялық объектілер т. б. ) қатысты.
Сондықтан, информацияның байқалу ықтималдылығы жөнінде айтуға болады:
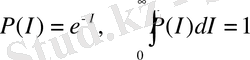 . (18)
. (18)
P ( I ) ықтималдықты f ( I ) ықтималдықтың таралу тығыздығының функциясы арқылы жазсақ:
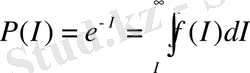 , (19)
, (19)
мұндағы интеграл шектері
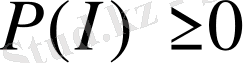 аймаққа сәйкес келеді. Демек,
аймаққа сәйкес келеді. Демек,
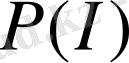 - информацияның байқалу ықтималдық функциясы
- информацияның байқалу ықтималдық функциясы
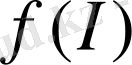 - ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.
- ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.
(18) формуланы ескере отырып, өзұқсас жүйелердің информациялық энтропиясын келесі түрде жазамыз:
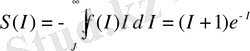 . (20)
. (20)
 үшін
үшін
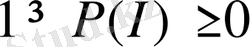 және
және
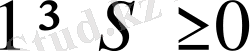 болады.
болады.
Өзқауымдық жүйенің өзұқсастығы қандай да бір сипаттамалы
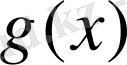 функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:
функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:
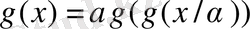 , (21)
, (21)
мұндағы
α
- масштабты көбейткіш. Кез-келген үздіксіз функция өзінің қозғалмайтын нүктесінде (21) теңдеуді қанағаттандырады. Сипаттамалық функция ретінде
f
(
I
) - ықтималдық тығыздығын және
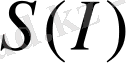 - информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:
- информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:
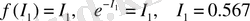 , (22)
, (22)
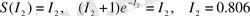 . (23)
. (23)
Бұл қозғалмайтын нүктелер бірмәнді орнықты, себебі олар, сонымен қатар, информацияның
 кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:
кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:
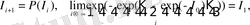 (24)
(24)
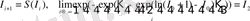 . (25)
. (25)
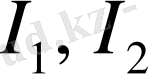 сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы - Фибоначчи санын (жүйенің динамикалық өлшемі - «алтын қима») қолдану аймағының кеңейуі.
сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы - Фибоначчи санын (жүйенің динамикалық өлшемі - «алтын қима») қолдану аймағының кеңейуі.
 саны информациялық (локальді) сипаттауына, ал
саны информациялық (локальді) сипаттауына, ал
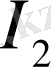 саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді.
саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді.
 болса (22) -ден (21) шығады,
болса (22) -ден (21) шығады,
 бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (23) -ден
бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (23) -ден
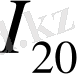 - Фибоначчи саны үшін теңдеу аламыз:
- Фибоначчи саны үшін теңдеу аламыз:
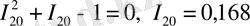 , (26)
, (26)
(21) теңдеуден I - I 10 = I 10 , I 10 = 0, 5.
Сонымен, тәжірибеде күрделі жүйенің өзқауым күйі S ∈[ I 20 I 2 ] жағдайда, қарапайым жүйенің өзұқсас жағдай I ∈[ I 10 , I 1 ] болғанда байқалуы тиіс.
Төменде (21), (22) тәуелділіктерді тұрғызуға арналған бағдарлама және сплайн интерполяцияның көмегімен тұрғызылған график келтірілген (3-сурет) .
I 1 , I 2 сандарының мағынасын жалпылама пайымдаулармен толығырақ ашуға болады. Шеннон бойынша Y берілген кездегі Х шамасы туралы информация шартсыз және шартты энтропиялардың айырымы ретінде анықталады:
- S(X) -S(X/Y) =I(X) > 0. (26)
- S(X) шамасын «Физикалық хаостың» энтропиясының анықталмағандығының нормасы ретінде қабылдап, (26) -ны мына түрде жазамыз:
I + S = 1, (27)
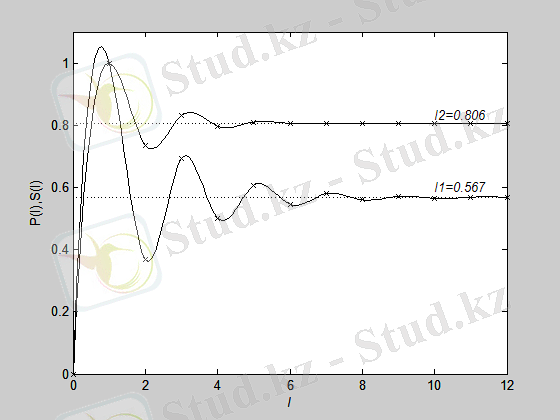
6-сурет. Информация және энтропияның сипаттық уақыт бойынша өзгерісі
- мұндағыI- анықталғандықтың салыстырмалы өлшемі (информация), S- қандайда бірХсипаттасы бойынша жүйе туралы анықталмағандықтың салыстырмалы өлшемі (энтропиясы) . Жалпы мағынада (27) өрнек кез-келген табиғаттың күрделі жүйелерін өзара байланысқан альтернативті сипаттамаларын байланыстырады: тәртіп және хаос, симметрия және асимметрия, рационалды және иррационалды, детерминизм және индетерминизм және т. б. Альтернативті сипаттамалардың үйлесімі олардың салыстырмалы өлшемінің өзгеруінің пропорционалдылығын болжайды:
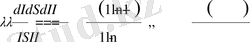 (28)
(28)
мұнда I , S өлшем бірліктерін таңдау еркіндігі мүмкін болғандықтан интегралдау тұрақтысы нөлге тең деп алынған. Дербес жағдайда λ параметріне және I айнымалысына айқын мағына беретін
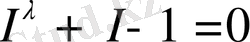 (29)
(29)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz