Энтропияның теориялық негіздері: термодинамикалық, статистикалық және информациялық интерпретациялары


- Энтропия түсінігі
Энтропия - бұл реттілік өлшемі, хаос өлшемі. Оның шамасы жүйенің реттелген, құрылған күйден алыс екенін, және толығымен хаостық, құрылымсыз, біртекті түрге жақын екенін көрсетеді. Бірақ, дәл сол дәрежеде энтропия сонымен қатар жүйенің құрылымды ұйымдастық өлшемі болады, Өйткені рет пен хаос - бұл қарама - қарсы және өзара толықтыратын түсініктер. Энтропия хаос немесе рет өлшемі ретінде әртүрлі табиғат жүйесінде байқалды: термодинамикадағы Клаузиус энтропиясы, статистикалық физикадағы Больцман энтропиясы, информация теориясындағы Шеннон энтропиясы, динамикалық жүйедегі Колмогоров энтропиясы, кванттық механикадағы фон Нейман энтропиясы. Энтропия жүйенің табиғатына тәуелсіз хаостық энтропия өлшемі ретінде универсалды болып табылады. Ашық жүйелер физикасының дамуымен әртүрлі макроскопиялық функциялар ішінде тек қана энтропия оны макроскопиялық жүйелердегі процестерді статистикалық бейнелеу өлшемі ретінде пайдалануға мүмкіндік беретін қасиеттердің жиынтығына ие болады.
1865ж. Рудольф Юлиус Эммануэль Клаузиусв жаңа термодинамикалық шама туралы түсінік енгізген ( еж. - грек. ἐντροπία - бұрылыс, айналу) . Бұл шама жылу энергиясын механикалыққа айналдыру, және керісінше айналдыру өлшемі болып табылады. Карно циклінде Q1/T1=Q2/T2 . Яғни Q/T қатынасы сақталады. Клаузиус dS=dQ/T дифференциалын енгізген, онда энтропия өсімшесі Т абсолют температурасына жататын dQ жылу энергиясының өзгерісі ретінде анықталады, және интеграл
S1(V1, T1) - S2(V2, T2) = ∫dQ/T=Q1/T1-Q2/T2 =0, (1. 10)
яғни (V, T) айнымалылар кеңістігінде интегралдау жолына тәуелді емес. Осылайша, S Клаузиус интегралы - жүйенің күй функциясы болып табылады. Клаузиус энтропиясының өлшем бірлігі - Дж/К. Өлшемсіз энтропияға оны Больцман тұрақтысына бөліп өтуге болады:
S=(1/k) ∫dQ/T, k=1. 38⋅10 -23 Дж/К. (1. 11)
Энтропия өзгерісі ең қарапайым термодинамикалық жүйелердің өзінде өте жоғары болады. Клаузиус энергия түрленулері туралы идеяны барлық процестерге таратып, әлемнің шарасыз жылулық өлімі туралы қорытындыға келеді.
XIX және XX ғасырладың басындағы ұлы физик Людвиг Больцман энтропияның кинетикалық мағынасын түсіндірді. Ол термодинамикалық жүйенің теңықтималды микрокүйлерінің P санының логарифмі Клаузиустың термодинамикалық энтропиясының барлық қасиеттеріне ие болатынын көрсетті. Ал егер оны k = 1. 38⋅10 -23 Дж/К тұрақтысына көбейтсе, онда мұндай функция Клаузиустың өлшемді энтропиясының физикалық мағынасында толығымен барабар болады
S = k log P. (1. 12)
Л. Больцман, 1877 жылы энтропияның статистикалы-физикалық анықтамасын бере отырып, энтропия жүйенің жеткіліксіз информациясын сипаттайтынын айтады. Яғни, энтропия біздің жүйе туралы біліміміздің өлшемі. Осылайша, Больцман бірінші болып энтропияның информациялық мағынасын байқады.
Больцманның меншікті энтропиясы (бір бөлшекке келетін) мынаған тең
SB=-k ∫μƒ(x, ν) logƒ(x, ν) dxdν+So , (1. 13)
мұндағы dx, dν - μ - алтыөлшемді фазалық кеңістіктің элементі, ƒ(x, ν) - таралу функциясы, So - еркін тұрақты. Сондықтан классикалық термодинамикада тек қана энтропияның әртүрлілігі туралы айтуға болады.
1984ж. Клод Элвуд Шеннон, хабарламаларды шулы желілер арқылы жіберуді зерттей отырып, хабарламаның қабылдағышы (receiver) және таратқышының көптеген балама күйлердегі Pi ықтималдықтың дискретті таралу шамасын енгізіп, және информацияны сандық теориясының негізі болған формуланы енгізеді:
Н=- ∑ni=1Pilog2 Pi , (1. 14)
мұндағы n - символдар саны, олардан хабарлама құралады, Н - анықталмағандық шамасы. Егер N - хабарламадағы барлық жіберілген және қабылданған символдардың саны болса, онда
Pi =mi /N (1. 15)
Pi - хабарламаның i -ші символдарының пайда болу ықтималдығы, mi -хабарламаның i - шісимволдардың кездесу саны. Ол Н шамасын энтропия деп атайды. I информациясын Шеннон хабарламаны алу кезінде энтропияның кемуі ретінде анықтайды: I=H1 -H2
Энтропияның көптеген анықтамаларының арасында ортақ не бар? Клаузиус энтропияның универсалды сипаттамасына сенімді және әлемдегі бүкіл процестерде ол уақыт бойынша дамудың бағытын анықтайды деп ұйғарады. Теңсіздік орта жағдайына көптеген әртүрлі жалпыланған энтропия бар. Бұл табиғаттағы дәрежелік заңдардың ерекше рөліне байланысты. Осындай жағдайлар үшін Рlog (Р) өрнегі адамның жұлдыз жарығының сандық-информациясы, хаосы, локалды еместігі, интенсивтілігін және т. б. қабылдау планында қолайлы аддитивті шама болып табылады. Сезім органдары Вебер - Фехнердің логарифмдік заңы бойынша жұмыс жасайды: түйсік интенсивтілігі стимул интенсивтілігінің логарифміне пропорционал. Осы тұрғыдан, S~ РΣlog(Р) энтропиясы қабылдау үшін ыңғайлы абстрактті аддитивті шама. Оның физикалық мағынасы Р - ықтималдық тығыздық аргументінің қандай мағлұматта және қалай анықталатындығына байланысты. Логарифмдер негізі мардымсыз және сол немесе басқа тапсырманың қолайлық түсінігінен шығады.
Осылай, Больцманның термодинамикалық энтропиясы уақыт өте максимумға ұмтылады. Шеннонның информациялық энтропиясы формулалардың сыртқы ұқсастығы кезінде өзін қарама-қарсы кейіпте ұстайды, уақыт өте минимумға ұмтылады. Бұл деректі информация теориясының түсінігін физикалық жүйелерге қолданған кезде ескеру керек. Ақ шу барлық жағдайда максимал энтропияға сәйкес келеді. Фракталдарды қарастырған кезде жүйенің максимал энтропиясы оның құрылымдық ұйымдасуының, яғни хаостық пен ретсіздіктің төменгі дәрежесіне сәйкес келеді. Төменгі энтропия жоғарғы құрылымдық ретсіздікке сәйкес келеді. Бұл жерде энтропия жүйенің құрылымдық ұйымдасуының өлшемі ретінде қолайлы. Бұл жағдайда энтропияны құрылымдық энтропия деп атаған жөн.
2. 3 Информациялық энтропия туралы түсінік Информациялық энтропия сөзіндегі «Информация» ұғымы әртүрлі мағынаға ие. Қоғамдық - саяси информация әлеуметтік жүйенің өзекті жаңалықтары туралы мәліметтердің жиыны болып табылады. Кибернетикада информация ұғымы сигналдарды сақтау, өңдеу және жіберумен байланысты. Ықтималдықтар теориясында информация аддитивті мөлшерлік өлшем ретінде кездейсоқ оқиғаларды бір-біріне қатысты ықтималдылығымен салыстыру арқылы енгізіледі. Барлық информация теориясы негізінде информацияны мөлшерлі бағалау жатыр. Қарапайым комбинаторикалық формада бұл тұжырымды Р. Хартли ұсынды, ал толық аяқталған түрін К. Шеннон тұжырымдады. Шеннон информация теориясы О және L екі таңбаның арасындағы (биттер арасындағы) қарапайым альтернативті таңдаудан шығады, ондағы L 1-ге, “иә”, “шындық” т. с. с. теңестірілсе, ал О 0-ге, “жоқ”, “жалған” теңестіріледі. Мұндай таңдау екі белгіден тұратын хабарды қабылдауға сәйкес келеді. Мұндай хабарда болатын информация мөлшері бірлік ретінде қабылданады және ол бит деп аталады. Сондықтан бит - екілік белгі және информация мөлшерінің өлшем бірлігі, ол екі байланысқан тең ықтималдықты таңдамадағы информация мөлшері ретінде анықталады. Айталық
 (2. 1)
(2. 1)
-
Х
және
Y
әріптерімен сәйкес белгіленген жүйенің күйін сипаттайтын айнымалылар жыйыны болсын. Егер
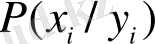 -
Х
жүйесі
-
Х
жүйесі
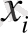 күйде болғанда
Y
у
i
күйіне өту ықтималдығы (шартты ықтималдық) болса, онда
Y
жүйесінің алған информациясы мынаған тең:
күйде болғанда
Y
у
i
күйіне өту ықтималдығы (шартты ықтималдық) болса, онда
Y
жүйесінің алған информациясы мынаған тең:
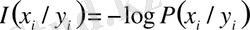 . (2. 2)
. (2. 2)
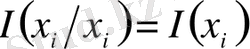 -
X
жүйесіндегі
-
X
жүйесіндегі
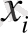 оқиғасына қатысты
оқиғасына қатысты
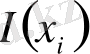 информация мөлшері деп аталады.
информация мөлшері деп аталады.
Ықтималдық
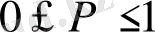 арасында жатқандықтан
I
әрқашан оң шама.
арасында жатқандықтан
I
әрқашан оң шама.
Логарифм негізін таңдауға байланысты информация мөлшері екілік, ондық және натурал логарифм бойынша: сәйкесінше бит, дит, нат - пен өлшенеді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz