Динамикалық жүйелер

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Динамикалық жүйелер

Динамикалық жүйелер ұғымы Ньютонның дифференциал-дық теңдеуімен сипатталатын қозғалысы механикалық жүйенің талдап қорытылған ұғымы түрінде пайда болды. Ол табиғаттың қай жүйесі болмасын физикалық, химиялық, биологиялық, экономикалық және сонымен қатар детерминделген жүйелер ғана емес, стохастикалық жағдайларын да қамтиды. Динамикалық жүйенің бейнелеуі сонымен қатар үлкен әртүрлікті қарастырады. Олар дифференциалдық теңдеудің көмегімен немесе логиканың алгебра функциясы, графтар, марковтық тізбектер және т. б тәрізді осындай амалдардың көмегімен жүзеге асады.

Қазіргі уақытта, динамикалық жүйенің тәртібін бейнелейтін математикалық модельдерімен өзгешенеленетін, осындай жүйелерді зерттеу үшін екі түрлі көзқарас қолданылады [1] .

1-ші көзқарас кезінде 5 динамикалық жүйенің математикалық моделі бірсыпыра уақыт кезеңіндегі жүйенің 5 бейнелеуімен түсіндірілетін х жағдайындағы ұғымға тұрақталады және осы жағдайдың х уақыт бойынша өзгерісін анықтайтын Т операторының ұғымына тұрақталады. Т операторы бірсыпыра келесі / + д/ уақыт кезеңінде дэл сол жүйелер х(і) бейнелеуі бойынша і уақыт моментінде х(г + м) бейнелеуін орындау арқылы процедураны көрсетеді. Егер Т операторы уақытқа нақты тәуелді болмаса, онда 5 жүйесі автономды деп аталады, ал қарама-қарсы жағдайда - автономды емес. 5 жүйесіндегі х жағдайын Ф кеңістіктің біраз нүктесі ретінде, мысалы координаттармен, импульстармен және 5 жүйесінің фазалық кеңістігі деп аталатындармен құрылуын қарастыруға болады. х жағдайының өзгерісіне Ф фазалық кеңістіктегі бейнелеуші деп аталатын сәйкес болатын нүктелер қозғалысы жауап береді. Осы кездегі бейнеленген нүктелер қозғалысы фазалық траектория деп аталатын қисықты сипаттайды. Фазалық кеңістік Ф және оператор Т динамикалық жүйенің математикалық моделін құрайды. Осындай көзқарас кезіндегі динамикалық жүйелердің көрсеткішін зерттеу, траекториядағы Ф фазалық кеңістіктің екпіндеу сипатын анықтауда және осы екпіндеудің құрылымының жүйенің физикалық параметрлерінің шамасына тәуелділігін анықтайды

Динамикалық жүйелерді зерттеудегі басқа көзқарас қарастырылған жүйенің функционалды жағын зерттеуге негізделген. Бұл көзқарас мүмкінеместілікке еріксіз көндіреді немесе қажеттілік жоқ кезіндегі динамикалық жүйенің ішкі құрылымының бүге-шігесіне дейін жетеді. Екінші көзқарас кезіндегі математикалық модель кірістік және шығыстық кеңістіктермен, сондай-ақ шығыстағы айнымалы кірістегі бірқатарлы түрлендірумен іске асатын оператормен анықталады. Бұл жақындауды есептегіш машиналардың автоматтық реттеу жүйесін, ізделген және өз бетімен оқылатын жүйелерді зерттеу кезінде қолданған ыңғайлы.

Динамикалық жүйедегі математикалық модельдің құрылымына тәуелділігін олардың Ф фазалық кеңістігі мен Т оператор түріне классификация жасауға болады. Үздіксіз және дискретті динамикалық жүйелердің күйін сипаттайтын х шамасы мәннің қандай қатар қабылдауына тәуелді фазалық кеңістіктің дискретті және үздіксіз жағдайларына бөлінеді.

Уақыт бойынша күй өзгерісі х-те үздіксіз немесе дискретті бола алады. Егер аі - кез-келген теріс емес сан жэне уақыт бойынша дискретті болса, егер м тек дискретті оң шамаларды ғана қабылдайтын болса, онда уақыт бойынша өзгеріс үзіліссіз. Т операторларын олардың қасиеті мен беру формасына байланысты бөлінеді. Егер Т операторы суперпозиция қасиетіне ие болса, онда ол сызықты деп аталады, егер Т операторы бейсызықты болса, онда соған сәйкес динамикалық жүйелер де бейсызықты деп аталады. Сонымен қатар Т операторы үздіксіз және дискретті болуы мүмкін. Т операторының тапсырма формасы дифференциалдық, интегралдық, матрицалық, таблицалық және т. б. болуы мүмкін.

Динамикалық жүйе екі топқа бөлінеді - консервативті (олардың қатарына үйкеліс жоқ кезіндегі механикалық тербелмелі жүйелер кіреді) және диссипативті. Диссипативті жүйенің өзгешелігі өзіне пайдалануға берілген ұзақ уақыт аралығындағы жүйеде пайда болған динамикалық режім бастапқы күйге тәуелді болмайды (қалай болғанда да бірқатар соңғы шегінде бастапқы шарт вариациясы кезінде) .

Диссипативті жүйенің фазалық кеңістігіндегі нүктелер жиыны орнықтырылған режімге келетін көптеген нүктелер аттракторлар деп аталады. Аттрактордың қарапайым мысалдары - периодикалық автотербеліс (бар көрші траекториялар жақындайтын жабық фазалық траектория) режиміне жауап беретін шекті кезең және орнықты тепе-теңдік күйі.

Бірінші бөлімде біз кәдімгі туындыдағы бейсызықты дифференциалды теңдеулермен сипатталанатын динамикалық жүйелерді қарастырамыз. Алайда динамикалық жүйенің қазіргі үғымы тек қана дифференциалдық теңдеумен ғана емес, қандай жолмен болмасын эволюция операторларының беру мүмкіндігін жобалайды. Соның ішінде соңғы уақыттарда теоретикалық зерттеулерде де, қолданбалы сипаттың жүмысындада рекурентті бейнелеумен сипатталатын дискретті уақыты бар жүйені өте жиі қарастырады. Осы жағдайда фазалық траекторияны фазалық кеңістіктегі біршама дискретті тізбектелген нүктелерді түсінуге болады.

Динамикалық жүйенің үлкен жетістігі - бейберекеттік динамиканың ашылуы болды. Бір қарағанда бейберекеттің пайда болуы - алғашқысы бойынша бірмағыналы болжаудың мүмкіндігімен жобаланған динамикалық жүйенің анықтамасымен сәйкес келмейді. Бірақ ешқандай үйлеспеушілік жоқ. Бейберекеттік режімде - бастапқы күй жүйесіндегі есепте қанша аз болса, дәлдік болмаса уақыт бойынша тез өсіп кетеді, сондықтан жеткілікті уақыт интервалында болжаулық қолдан келмейтін іс бола бастайды. Осындай режім түрі жүйелі емес, динамикалық айнымалының бейберекет өзгерісі уақыт бойынша сипатталады. Диссипативті жүйедегі фазалық кеңістіктегіі қүрылымға көрсету жасайтын күрделі түрғызылған жиындар - әуейі аттракторлар жауап

береді.

Математикалық маятниктің еркін тербелістері

Тербелістер туралы есептер физиканың барлық салаларында кездеседі. Көп жағдайларда мүлдем өзгеше физикалық объектілердің тербелістері бір-біріне ұқсас. Қарапайым мысалдар - маятниктің шағын тербелістері және конденсатор мен шарғыдан тұратын тізбектегі электр тербелістері.

Ұзындығы Ь қатты сырықтың бір шетіне қадалған, екінші шеті ілу нүктесінде бекітілген (1-сурет), массасы т жүктің қозғалысын қарастырайық. Жүктің қозғалысы центрі 0 нүктесі Ь радиусты шеңбердің дұға бойынша жүргендіктен, жүктің орны сырықтың вертикальдан ауытқу бұрышымен сипатталады. Програм-маның мәтінімен салыстыруға ыңғайлы болу үшін маятниктің вертикальды бағыттан ауытқу бұрышын . х-пен белгілейміз.

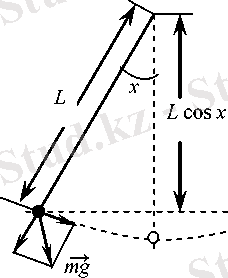
$C:\Users\User\Downloads\media\image1.png$

1-сурет.

Математикалық маятник

Маятниктің аз мәнді қозғалысы жақсы белгілі - бұл гармониялық тербелістер. Маятниктің қозғалыс заңы келесі түрде жазылады:

х = асо$ір ₀ і + (р ₀ , (1)

мүнда са ₀ - тербелістердің жиілігі, а - амплитуда, <р ₀ - бастапқы фаза. Егер ауытқулар аз болмаса, тербелістер сипатталатын теңдеуі

х + а>1 зіп х = 0. (2)

(2) -теңдеу бейсызық, оның шешімі, басқа көп бейсызық теңдеулердің шешімдері сияқты элементарлы функциялармен келтірілмейді, сондықтан оның сандық шешімін алу қажет. Жеткілікті аз ауытқу бүрышы кезінде (§іпх~х, мұнда . х-пен маятниктің ауытқу бұрышы белгіленген) теңдеу сызықты болады х+® ₀ ² х = о , оның шеіпімі (І) -түрде жазылады.

Маятниктің қозғалысының зерттеу нэтижелерін 4, р жазықтықта қисықтар жиныға ретінде салу ыңғайлы, мүнда р = х - бүрыштың өзгеру жылдамдығы. С, р] жазықтығы фазалыц жазыцтыц деп аталады, ал х = хі^р = ріі параметрлік қозғалыс заңымен анықталатын қисықтар - фазалық траекториялар.

Сызықты осциллятордың фазалық траекториялары энергияның сақтау заңымен берілетін эллипс болады. Математикалық маятник үшін бұл аз ауытқу бұрышы кезінде әділ. Үлкен ауытқу бұрышы кезінде математикалық маятниктің қозғалысы күрделі болады: тербелістерден басқа маятник жан- жаққа айналу мүмкін.

(2) -теңдеудің аналитикалық шешімі өте күрделі болғандықтан, маятниктің қозғылысын біз сандық түрде зерттейміз. (2) -теңдеуді бірінші ретті теңдеулер жүйесі ретінде жазайық