Астрофизикалық объектілерді фракталды және мультифракталды талдау


Астрофизикалық объектілерді фракталды талдау
Қазіргі таңда фракталдар мен мультифракталдар теориясытүрлі физикалық жағдайларда байқалатын өзұқсас қасиеттерді және күрделі скейлингті сипаттау үшін кеңінен пайдаланылады. Фракталдар қатарына геометриялық объектілер - қатты тілімденген пішінге ие және масштабтардың кең диапазонында әлдебір қайталанушылықты көрсететін сызықтар, беткейлер, денелер жатады. Қайталанушылық толық (бұл жағдайда тұрақты фракталдар туралысөз болады) немесе кездейсоқтықтың кейбір элементтері байқалуы мүмкін (мұндайфракталдарды кездейсоқ фракталдар деп атайды) . Кіші масштабтардағы кездейсоқ фракталдардың құрылымы бүкіл объктінің құрылыма сәйкес болып табылмайды, алайда олардың статистикалық сипаттамалары сәйкес келеді, өзұқсас қасиеттері объектіні статистикалық тұрғыдан тәуелсіз іске асыру бойынша орташаландырудан кейін сақталады.
Фракталдарға сандық сипаттама беру үшін, бір ғана шаманың - масштабы өзгерген жағдайда геометриясының немесе статистикалық сипаттамасының сақталуы қамтамасыз ететін Хаусдорф өлшемділігі немесе скейлинг көрсеткіші жеткілікті. Алайда, физикада, химияда, биологияда және басқа да ғылымдарда фракталдардың скейлингтің бір ғана көрсеткішінен артық көрсеткіштерге ие күрделі құрылымдарға таралуын қажет ететін көптеген құбылыстар кездеседі. Мұндай құрылымдар көрсеткіштердің тұтас спектрімен жиі сипатталады, Хаусдорф өлшемділігі олардың бірі ғана болып табылады.
Бастапқыда фрактал ұғымы физикада жағалау сызығының ұзындығын анықтау туралы мәселемен байланысты туындады. Қолда бар жергілікті карта бойынша оны өлшеу кезінде, қызықты бір дерек айқындалды - неғұрлым ірі масштабты карта алынатын болса, осы жағалау соғұрлым ұзын болып көрінеді.
Негізінде, осы өлшемдердің нәтижесі түрліше болады екен. Масштабты
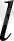 кішірейткенде, ұзындықтың барған сайын үлкен мәндеріне ие боламыз. Біртегіс қисықтан айырмашылығы, теңіз жағалауының сызығы көбіне тілімденгені соншалық (ең кішкентай масштабтарға дейін),
кішірейткенде, ұзындықтың барған сайын үлкен мәндеріне ие боламыз. Біртегіс қисықтан айырмашылығы, теңіз жағалауының сызығы көбіне тілімденгені соншалық (ең кішкентай масштабтарға дейін),
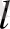 буыны ұзындығы кішірейген сайын,
L
шамасы - жағалау сызығының ұзындығы - түпкі шекке ұмтылмауы, дәрежелік заң бойынша ұлғаюы тиіс:
буыны ұзындығы кішірейген сайын,
L
шамасы - жағалау сызығының ұзындығы - түпкі шекке ұмтылмауы, дәрежелік заң бойынша ұлғаюы тиіс:
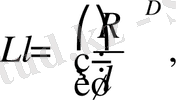 (1. 1)
(1. 1)
мұнда D > 1 - дәреженің кейбір көрсеткіші, ол жағалау сызығының фракталды өлшемділігі деп аталады. D шамасы неғұрлым үлкен болса , осы жағалау сызығы соғұрлым тілімденген болып табылады. (1. 1) тәуелділігінің келіп шығуы интуициялық тұрғыдан түсінікті: неғұрлым кіші масштабты пайдалансақ, соғұрлым кіші жағалау бөлшектері ескеріледі және өлшенетін ұзындыққа үлес береді. Керісінше, масштабты ұлғайта отырып, біз L ұзындығын азайту арқылы жағалауды «түзулейміз» .
Қатты масштабтың
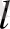 көмегімен жағалау сызығының ұзындығын
L
анықтау үшін,
көмегімен жағалау сызығының ұзындығын
L
анықтау үшін,
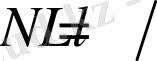 қадам жасау керек, мұнда
L
шамасы
қадам жасау керек, мұнда
L
шамасы
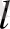 -ден
-ден
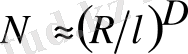 заңы бойынша
N
заңы бойынша
N
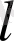 -ге тәуелді болатындай етіп өзгереді
.
Нәтижеде масштаб кішірейген сайын жағалау сызығының ұзындығы шексіз ұлғая түседі. Бұл жағдай фракталды сызықты кәдімгі біртегіс сызықтан (шеңбер, эллипс типі) бірден ерекшелейді, аппроксимациялаушы сынған
L
ұзындығының шегі оның буынының ұзындық нөліне ұмтылғанда,
-ге тәуелді болатындай етіп өзгереді
.
Нәтижеде масштаб кішірейген сайын жағалау сызығының ұзындығы шексіз ұлғая түседі. Бұл жағдай фракталды сызықты кәдімгі біртегіс сызықтан (шеңбер, эллипс типі) бірден ерекшелейді, аппроксимациялаушы сынған
L
ұзындығының шегі оның буынының ұзындық нөліне ұмтылғанда,
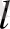 түпкілікті болады. Нәтижеде біртегіс қисық үшін оның фракталды өлшемділігі
D
= 1 болады, яғни топологиялыққа сәйкес келеді.
түпкілікті болады. Нәтижеде біртегіс қисық үшін оның фракталды өлшемділігі
D
= 1 болады, яғни топологиялыққа сәйкес келеді.
d
- фракталды объект тұратын кеңістіктің қарапайым Евклид өлшемділігі болсын делік
(d =
1 - сызық,
d
= 2 - жазықтық,
d
= 3 - кәдімгі үш өлшемді кеңістік) . Енді осы объектіні тұтас
d
-өлшемді
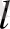 радиус «шарларымен» жабайық. Бұл үшін кемінде
радиус «шарларымен» жабайық. Бұл үшін кемінде
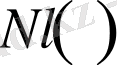 шар қажет делік. Сөйтіп, егер жеткілікті кіші
шар қажет делік. Сөйтіп, егер жеткілікті кіші
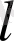 жағдайында
жағдайында
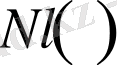 шамасы
шамасы
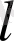 -ден дәрежелік заң бойынша өзегеретін болса,
-ден дәрежелік заң бойынша өзегеретін болса,
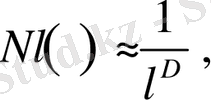 (1. 2)
(1. 2)
онда D - осы объектінің хаусдорфтық немесе фракталды өлшемділігі деп аталады.
(1. 2) формуласын келесі түрде де қайта жазуға болады:
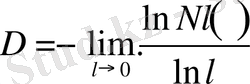 (1. 3)
(1. 3)
Бұл D фракталды өлшемділігінің жалпы анықтамасы қызметін атқарады . Осыған сәйкес D шамасы осы объектінің жергілікті сипаттамасы болып табылады.
Реттілік пен ретсіздік мәселесі динамикалық астрономияда маңызды қосымшаға ие . Динамикалық жүйелердің көптеген басты ұғымдары өз мәнін галактикалық, жұлдыздық және планеталық құрылымдар және олардың эволюциясы туралы заманауи түсініктерден табады. Бұл түсініктер аналитикалық және басқа да сандық әдістерді пайдалана отырып, N -дене мәселесін қоса алғанда, аспан және статистикалық механикадан алынған жақсы танымал мысалдармен нығайтылады. Сондықтан динамикалық астрономия - бұл гидродинамика, геофизика, биология, плазма физикасы, космология және т. б. сияқты заманауи ғылымдардың басқа да көптеген салаларымен қатар реттілік пен ретсіздіктің іргелі тұжырымдамалары көрініс табатын сала деп айтуға болады.
Динамикалық астрономияның кейбір жалпы тұжырымдамалары жұлдыз - галактикалық және планеталық жүйелер бақылауымен нығайтыла түседі. Ретілік пен ретсіздіктің үйлесімін галактикалардың құрылымы мен динамикасының маңызды тетігі деп санау керек. Олардың шектелген саны ғана сфералық потенциалмен сипатталады, алайда көпшілігі өстік немесе үшөстік симметрияға ие. Соңғы жағдайда потенциал қатты деформацияланып, күшті реттелмеген бейберекет қозғалыстар орын алады.
Жұлдыздардың, галактикалардың үлестіруі, галактикалар шоғыры және тағы сол сияқты материялар ілгеріден бері әуесқойларды да, мамандарды да қызықтырып келеді, алайда кластеризация астрофизикада әлі күнге зерттелмеген. Негізгі мәселелердің бірі - неліктен материялардың үлестіруі тұрақсыз иерархиялық заңдарға, ең болмағанда, масштабтардың белгілі бір диапазонында бағынады.
Жағдайды іргелі ұстаным тұрғысынан қарастыра отырып, тұрақсыз иерархиялық заңдарға қатысты болмау ниеті оны математикалық тұрғыдан сипаттайтын аспаптардың болмауынан келіп шықса керек. Статистикадан екі жорамалдың ішінен мұқият зерттелген деп біреуін ғана таңдау талап етіледі.
Алдыңғы жұмыстарда [1, 127 б. ] деректерді масштабтық-инварианттық фракталды тозаң туралы ұғым аясында түсіндіруге болады деп тұжырымдайтын жұлдыздар мен галактикалардың теориясы ұсынылды. Жұлдыздар мен галактикалардың таралуы кейбір өзұқсас аумақты құрайды, оның ішінде фракталдық өлшемділік
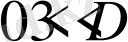 теңсіздігін қанағаттандырады .
теңсіздігін қанағаттандырады .
Ғарыш жасалымдары бірін-бірі қармайтын құрылымдар иерархиясын құрайды (жұлдыз - жұлдыз шоғыры - галактика - галактикалар шоғыры және т. б. ) . Атап айтсақ, біз бақылап отырған әлем (радиусы 15 млрд. жарық жылына жуық) ең кішісі өз ішінде біздің көру көкжиегімізден құралатын, бірін-бірі қармайтын ықшам ғарыш жасалымдарының реттілігіне кіреді, оны біздің Метагалактикамыз деп атау керек.
Қазіргі таңда жалпы қабылданған Әлемнің фридмандық моделі космологиясында Әлем біртекті және массаның соңғы тығыздығына ие деп болжанады. Сонымен қатар қазіргі таңда суреттелетін Әлемнің фракталдығы бір кездері табиғи деп саналған болжамдарды дұрыс емес деп көрсетеді. Біздің планетамыз Күн жүйесіне кіреді, Күн басқа жұлдыздармен бірге галактиканы құрайды, галактикалар құрылымдана келіп, галактикалар шоғырын түзеді және т. б. Жұлдыздар арасындағы қашықтық жұлдыз жүйесіндегі планеталар арасындағы қашықтықтан әлдеқайда көп. Галактикалар арасындағы қашықтық жұлдыздар арасындағы қашықтықтан көп және т. б.
Ерекше сиретілген және иерархияланған күйде бола тұрып, ғарыш құрылымдары фракталды болып келеді, мұны бірқатар авторлар растайды. Осы фактінің қабылдануы басқа бір жайтпен күрделене түседі: 300 млн. жарық жылында немесе одан көп қашықтықта біздің Метагалактикамыз (макро) біртекті болып келеді. Сондай-ақ фракталды құрылымдары маңызды түрде біртекті емес.
Галактиканың фотосуретінде жарқыраудың үлестіруі оның морфологиялық типін анықтайды. Осы бір тікелей бақыланушы үлестіру пен галактикалық зат динамикасы арасында байланыс орнату қызықты жайт болып табылады. Мысалы, галактикалардың түсі Е - жүйелерден Ir - жүйелерге қарай өзгере түседі: Ir - галактикалар ең көгілдірі, S - галактикалар қызыл, ал Е - галактикалар ең қызылы болып келеді.
Галактиканың түсі, оның жарқырауы мен айналу жылдамдығы галактиканы біртұтас бүтін ретінде сипаттайды, ал морфологиялық типі дискі бойынша заттың жарқырауының жергілікті бөлінуімен байланысты. Галактиканың сандық морфологиялық типін дискі бойынша жарықтың таралуының
 фракталды өлшемділігі деп сипаттауға болады.
фракталды өлшемділігі деп сипаттауға болады.
Хаусдорф өлшемділігі ғарышта байқалатын түрлі күрделі құрылымдарды санмен салыстыруға мүмкіндік береді екен. Асашоғырлануда галактикалардың кеңістіктік үлестіруінің фракталды қасиеттеріне жуырда ғана Тарту обсерваториясында өз қызметкерлерімен бірге Я. Эйнасто талдау жасады. Бикеш шоқжұлдызындағы асашоғырлану
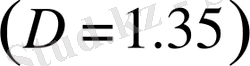 құрылымын танытатындығы анықталды. Асашоғырлану масштабтарынан асып түсетін кеңістіктік масштабтарда (300 Мпк), галактикалар үлестіруінің хаусдорф өлшемділігі үш өлшемді кеңістіктің топологиялық өлшемділігіне жуық болып келеді. Егер бақыланушы Әлемде заттардың үлестіруі үлкен кеңістіктің масштабтарда біртекті болса, осылай болуы керек.
құрылымын танытатындығы анықталды. Асашоғырлану масштабтарынан асып түсетін кеңістіктік масштабтарда (300 Мпк), галактикалар үлестіруінің хаусдорф өлшемділігі үш өлшемді кеңістіктің топологиялық өлшемділігіне жуық болып келеді. Егер бақыланушы Әлемде заттардың үлестіруі үлкен кеңістіктің масштабтарда біртекті болса, осылай болуы керек.
Галактиканың дискі бойынша жарқырау үлестіруінің фракталды қасиеттері галактикада болатын физикалық үдерістерге байланысты. Сондықтан бақыланушы жарық үлестіруінің
D
фракталды өлшемділігі галактиканың физикалық қасиеттеріне байланысты. Мысалы,
Е
- галактикалардан
S
- галактикаларға өткенде, фракталды өлшемділік азаяды. Галактикалық құрылымның пайда болуының әрбір моделі үшін,
 теориялық мәнін есептеп, бақыланушы фракталды өлшемділікпен салыстыру керек.
теориялық мәнін есептеп, бақыланушы фракталды өлшемділікпен салыстыру керек.
Галактикалардың спиральды өрнегі - орасан зор масштабта ортаның реттелген қозғалысына тамаша мысал болып табылады. Спиральды бқтақтардың ені мың парсекке жетеді. Жүздеген миллион жыл ішінде спиральды өрнек өмір сүреді.
Спиральды өрнектің пайда болуы галактиканың айналуымен және галактикалық ортада динамикалық тұрақсыздықтың дамуымен байланысты. Бұрыштық айналу жылдамдығы орталықтан қашықтықтың өсе түсуіне орай азая береді. Бұрыштық жылдамдықтың қашықтыққа тәуелділігі галактикалық заттың әрбір бөлшегі жүйенің орталық аумақтарына еркін түсетін жағдайға ұқсас. Кейбір кезеңде заттар үлестіруінде жұлдызды жүйенің радиусы бойлап орналасқан біртектілік еместік орын алады. Ішкі аумаққа қарағанда, сыртқы аумақтар баяу айналатындықтан, уақыт өте келе біртектілік еместік спиральға ұласады. Кез келген табиғаттың біртекті еместігі осындай формаға ие болады екен. Мысалы, егер кейбір кезеңде тығыздықтың жергілікті ұлғаюынан гравитациялық өрістің жергілікті ауытқуы туындаса, дискі бойлап гравитациялық потенциалдың спиральды толқыны жүгіретін болады. Осы айнымалы потенциал қатарында тығыздық толқыны деп аталатын заттардың кезеңдік қоюлануы туындайды. Спиральды құрылым толқын үдерісі болып табылатындығын өз Галактикамыздағы жұлдыздар жылдамдығы қатарын зерттеу жұмыстары растап отыр. Астрономдар Е. Д. Павловская, Ю. Н. Мишуров және А. А. Сучков жұлдыздар жылдамдығының қатары спиральды пішіннің кезеңдік құрылымына ие екендігін көрсетті.
Жұлдыздардың күрделі құрылымын, оның ішінде фракталдығын ұғыну үшін, олардың эволюциясын қысқаша сипаттап өтейік. Туылғаннан өлгенге дейінгі бірізді эволюция циклынан өтетін жұлдыздар негізгі қолжетімді астрофизикалық объектілер болып табылады. Жұлдыз эволюциясының барысында, атап айтсақ, галактикада массалары әр түрлі жұлдыздар туылғанда, массаның бастапқы функциясына (IMF) жауап беретін алғашқы жуысуда толық белгілі бір реттілік байқалады, аккрециялаушы массалы жұлдыздардар аумағындағы еңісі Салпитердің белгілі функциясына сай келеді.
Жұлдыздың пайда болу ошақтары генетикалық тұрғыдан массалық, салыстырмалы түрде жазық галактикалық дискімен байланысты, оның симметрия жазықтығында тығыздығы біртекті бөлінбеген газ бен тозаңның қоспасы түріндегі көзге көрінетін зат шоғырланады. Мұндай көпфазалы, көпкомпонентті орта гравитациялық қысу барысында тұрған және жұлдыз жиынтықтары мен ассоциацияларының ерте қалыптасу сатысы болып табылатын массалық салқын тығыз бұлттарға тән болып келеді. Дискілік галактикаларда жұлдыздың пайда болуы ~ 10 7 M S массалы және газ дискінің қалыңдығындағы өлшемде келетін ОВ-ассоциацияларда белсенді орын алады, сөйтіп коллапс барысында жинақталудың 90%-ға жуығы ~ 10 3 M S массалы жұлдыздарға ыдырайды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz