Астрофизикалық джеттер мен ағын лақтыруларды математикалық және суперкомпьютерлік моделдеу

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Астрофизикалық ағын лақтыруларды моделдеу

Астрофизикада, нақтырақ айтқанда, биполярлық ағындық лақтырулардың пайда болу проблеммасы қарсаңында, математикалық моделдеу әдісі мен есептік эксперементтер, жұлдыздық объектілерде өтетін процесстер табиғаты мен механизмдерін зерттеудегі негізгі құралдардың бірі болады. Жағдайдың осындай болуына астрофизикалық объектілердің орталық облыстарын тікелей бақылуға мүмкіндік беретін техникалық әдістер мен құралдардың жоқ болуы себеп. Осыған байланысты джеттерді, ағын лақтыруларды тудыратын жүйенің механизмдерін тікелей бақылаулар арқылы зерттеу мүмкін емес [1, 2] .

Замануи телескоптардың рұқсат ету дәлдігі тек қана қалыптасқан лақтырулар мен оны айнала орналасқан жарқыраған газ бұлтын көруге мүмкіндік береді. Бірақ осы бұлттың арасында орналасқан, ағын энергиясының көзі болатын, гравитациялық өрісі орасан зор, шағын объект пен сипатты өлшемі бірнеше парсек болатын джеттаның негізін көру мүлде мүмкін емес

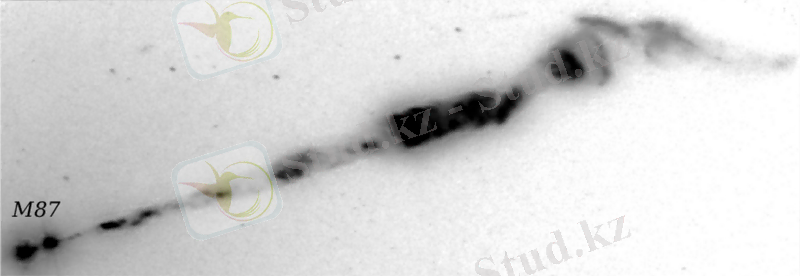
1. 6 сурет - Хаббл телескобымен түсірілген M87 галактика джеті [3]

Осымен қатар джет лақтыруларды үдететін жүйенің орталық аймақтары туралы нақты бақыланған нәтежелердің болмауы, келтірілген есептерге сандық, компьютерлік моделдеу әдісін қолдану ерекшеліктерін анықтайды.

Моделдеудің пәні тек қана бақыланған нәрселердің сандық параметрлерінің нақты да дәл қатынастары емес, осыған қоса бақыланған процесстердің сапалы спаттамаларының зерттелуіне негізделеді.

Сандық эксперементтер мен моделдеулердің мақсаты ретінде, бір жағынан, астрономдардың тіркеген мәліметтерін, екінші жағынан лақтырулар түзілуінің нақты шарттарын түсіндіруді қамтамасыз ететін эффектер мен механизмдерді ескере отырып зерттеу болады.

1. 2. 4. Суперкомпьютерлерде моделдеу

Галактикалардың тығыз жиындарда қозғалуы - олардың арасындағы соқтығыстарды маңызды эволюциялық факторға айналдырады. Галактикалар эфолюциясында маңызды рөл ойнайтын, бақылануы қиынға түсетін, галактиканың газ компонентасының кеңістіктік динамикасын зерттеу - негізігі қызығушылық тудыратын мәселен. Осыған сәйкес, галактикалар соқтығысының газодинамикалық жуықтауға негізделген суперкомпьютерлік моделдеудің қажеттілігі туады [4 - 8] .

Алғашында құрылымы жоқ космостық хаостан, реттелген құрылымдардың түзілуі мен тұрақты болуы шарттарын зерттейтін, эволюциялық теорияға негізделген, заманауи астрофизикалық бақылаулармен салыстыра отырып тексеруге болатын компьютерлік моделдер құру - негізгі мақсат.

Астрофизикалық құбылыстар бір - бірімен байланысқан ауқымды масштабтағы физикалық процесстердің жиынтығы болатынын ескерсек, бұл бағыттағы математикалық моделдеудің маңыздылығы артатыны айқын. Бұған негізгі себеп, физикалық процестердің қандай да болса түрлерінің бір - біріне әсерлесуін моделдеуге мүмкіндік беретін, соңғы уақыттағы информациялық - есептеу технологияларының шапшаң дамуы [9, 10] .

Осыған сәйкес суперкомпьютерлік модельдеудің бір бағыты - Бейнелеу бір уақытқа байланысты динамикалық жүйе қасиеттерінің өзгерісінің графикалық көрінісі - жүйе элементтерінің әрқайсысы үшін уақыт пен кеңістікке сәйкес функционалды тәуелділігі бар жүйе. Бұл математикалық абстракция кез келген жүенің уақытқа байланысты эволюциясын зерттеуге не сипаттауға мүмкіндік береді.

Динамикалық жүйе күйі уақыттың кез келген мезетінде күй кеңістігінде нүктеге сәйкес заттық сандардың көптілігімен сипатталады. Динамикалық жүйенің эволюциясы детерменделген функциямен сипатталады. Яғни берілген уақыт интервалынан кейін, осыған дейінгі күйіне сәйкес, жүйе нақты, келесі күйге ие болады.

Динамикалық жүйе деп, қандай да бір объектінің, процестің немесе уақиғаның математикалық моделі ретінде түсінеміз. Айтылған бойынша, динамикалық жүйе - жалпы кез келген жүйенің бір күйінене екінші күйне өту процесін сипаттайды. Фазалық кеңістіктегі бейнелеу - динамикалық жүйенің барлық мүмкін бола алатын күйлерінің жиынтығы. Осылайша, динамикалық жүйе өзінің бастапқы күйі мен келесі күйіне өтуін қамтамасыз ететін заңдар және олардың жиынымен сипатталады.

Динамикалық жүйе (уақыт бойынша дискретті де, үздіксіз д(е), кез-келген облыста беріліп, осы жерде бар болу теоремасы мен дифференциалды өрнектің жалғыз шешімі болу шартын қанағаттандыратын, дифференциалды теңдеулердің автономды жүйесімен сипатталады. Динамикалық жүйенің тұрақтылық күйлеріне дифференциалды теңдеудің айрықша нүктелері сәйкес келеді. Ал бұл жүйенің периодты шешімдері сәйкесінше тұйықталған фазалық қисықтармен сипатталады.

Қазіргі таңдағы бұл ғылымның атауына математиканың барлық салаларында кездесетін, солардың ішінде: топология мен алгебра, алгебралық геометрия, өлшемділік теориясы, дифференциалдық формалар теориясы, ерекшеліктер мен апаттар теориясы аппараттарын эффективті де ұтымды қоданып, физикалық заңдылықтарды түсіндіруді жүзеге асыратын әдістемелердің жалпылама жиыны тән [11, 12]

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.