Күн белсінділігін рекурренттік талдау әдісімен зерттеу нәтижелері

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

2. 3 Фракталдық өлшемділік

Евклид кеңістігіндегі өлшемі L фракталдық объектіні қарастырайық. Мұнда біз тек, бос емес, яғни ішінде кем дегенде бір нүктесі бар ұяшықтарды ескереміз. Бос емес ұяшықтардың i нөмері i = 1, 2, . . . N ( δ ) аралығында өзгерсін, мұндағы N ( δ ) ұяшықтың δ өлшеміне тәуелді - бос емес ұяшықтардың жалпы саны. Егер ұяшықтар бойынша нүктелердің таралуы бір келкі болмаса фрактал біртексіз, яғни мультифрактал ретінде қарастырылады. Мультифракталды сипаттау үшін ℒ облысындағы берілген нүктелердің таралуын сипаттайтын D _q жалпыланған фракталдық өлшемділіктер енгізіледі.

n _i (δ) -i-ші нөмерлі ұяшықтағы нүктелер саны болсын, онда

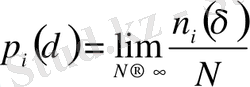(2. 11)

шамасы көп нүктелерден кездейсоқ алынған нүктелердің i -ші ұяшықта жататындығының ы (25)

мұндағы 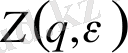- жалпыланған статистикалық қосынды:

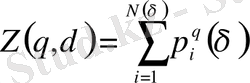Егер D _q = D = const, яғни q -ға байланысты болмаса, бұл тек бір ғана шамамен - D фракталдық өлшемділікпен сипатталатын нүктелер жиыны жәй, регулярлы фрактал болады. Керісінше D _q функциясы q мен бірге өзгерсе онда қарастырылып отырған жиын мультифрактал болады. 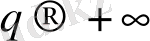жағдайда (2. 1) жалпыланған статистикалық қосындыға ең көп n _i бөлшектері бар ұяшықтар көп ықпал етеді, сондықтан олар ең көп p _i толтырылу ықтималдығымен сипатталады. Керісінше 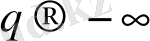ұмтылғанда (26) жалпы статистикалық қосындыға ең аз толған ұяшықтар, яғни p _i -дің аз мәндері көп ықпал етеді. Осылайша, D _q функциясы, зерттеліп отырған ℒ нүктелер жиынының қаншалықты біртексіз екендігін көрсетеді .

Жалпы жағдайда мультифрактал, статистикалық қосындының 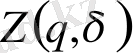δ → 0 ұмтылғандағы қасиетін анықтайтын, қандайда бір 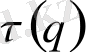бейсызық (25) функциямен сипатталады. Бірақ нүктелердін таралуын сипаттау үшін 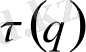функциямен қатар оның туындысын да білу қаже т:

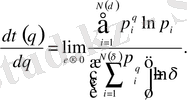(2. 12)

Бұл туынды q мен бірге өзгереді.

q = 1 болғанда жалпыланған фракталдық өлшем:

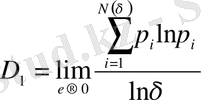. (2. 13)

Бұл формуланың алымы, таңбасын ескергенде, фракталдық жиынның энтропиясы болып келеді. Нәтижесінде D ₁ жалпыланған фракталдық өлшем S ( δ ) энтропиямен келесі қатынаста болады:

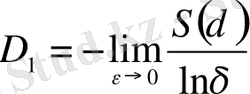. (2. 14)

Бұдан,

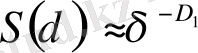, (2. 15)

Яғни, D ₁ дегеніміз нүктенің қандайда бір ұяшықта орналасу орнын анықтайтын информацияны сипаттайды. Осыған байланысты D ₁ жалпы фракталдық өлшемділікті көп жағдайда информациялық өлшемділік деп атайды. Бұл δ ұяшықтың өлшемі нөлге ұмтылғанда, нүктенің орнын анықтау информациясы қалай өсетіндігін көрсетеді.

2. 4 Корреляциялық өлшемділік

Бірдей өлшемді δ ұяшықтарға бөлінген фракталды бетті қарастырайық және кез-келген х ₁ және х ₂ еркін таңдалған екі нүкте фракталды объектіге жататын нүктелер болсын делік. _. Екі нүктеніңде i -ші ұяшықта болу ықтималдығы қанша? Бір нүктенің осы беттің i -ші элементіне түсу ықтималдығы р _i -ге тең. Егер екі нүктенің осы ұяшыққа түсуі байланыссыз оқиғалар деп алсақ, онда оның ықтималдығы 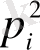-ге тең болады.

Фракталдық бет ( q = 2) жабылатын ұяшықтар көлемін кішірейткендегі, статистикалық қосындының (26) өзгерісін қарастырайық. δ - ны кішірейткенде қосынды азаяды, бұдан ол дәрежелік заңға бағынады деп жорамалдауға болады:

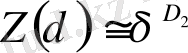, (2. 16)

немесе, эквивалентті, шек

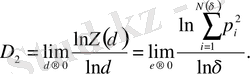(2. 17)

D ₂ корреляциялық өлшемділік деп аталады.

Паккард-Таккенс әдісіне қоса орташа күн магнит өрісінің уақыттағы өзгерісі 2 тараудың 3-4 бабында көрсетілген рекурренттік талдау әдісімен зерттелген. Бұл зерттеу нәтижелері

3. 18 сурет - 1979 - 1982 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

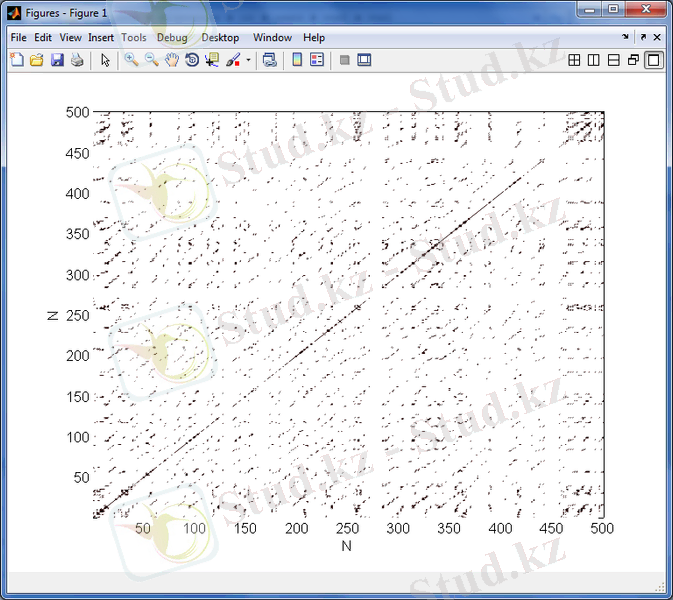
3. 19 сурет - 1979 - 1982 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің

фазалық портреті

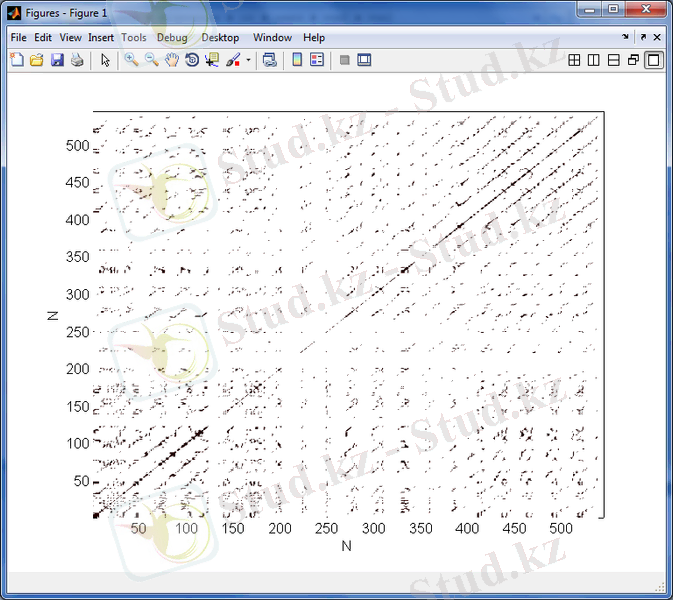
3. 20 сурет - 1989 - 1992 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

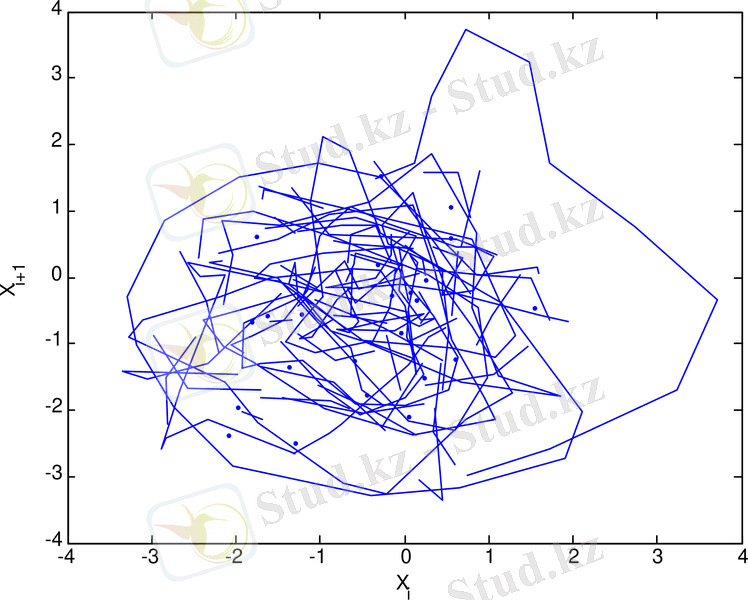
3. 21 сурет - 1989 - 1992 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің фазалық портреті

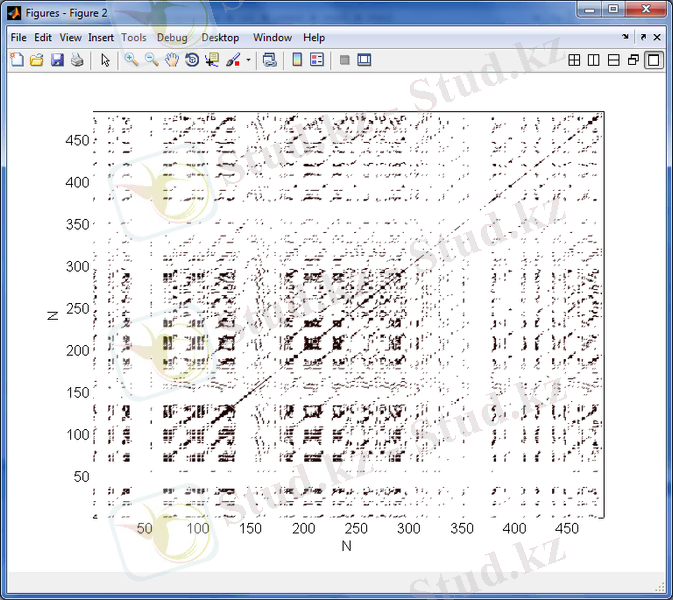
3. 22 сурет - 1999 - 2002 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

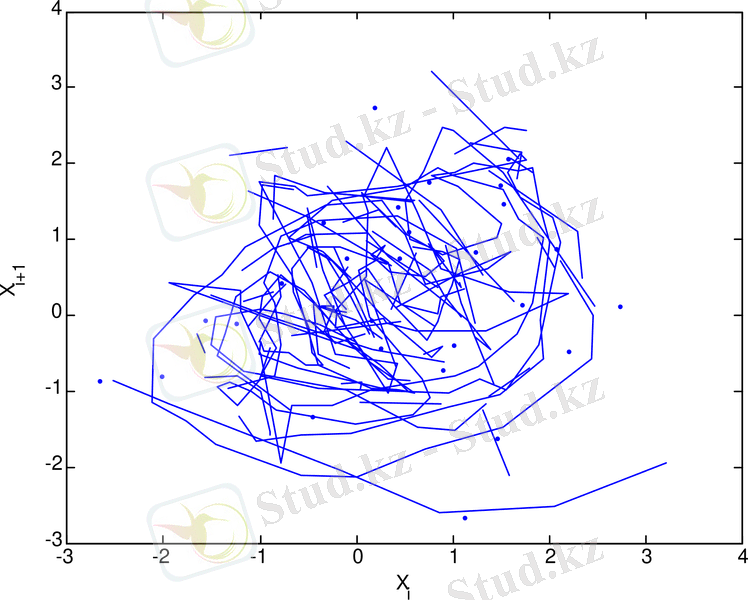
3. 23 сурет - 1999 - 2002 жж аралығындағы күн белсенділігінің максимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің фазалық портреті

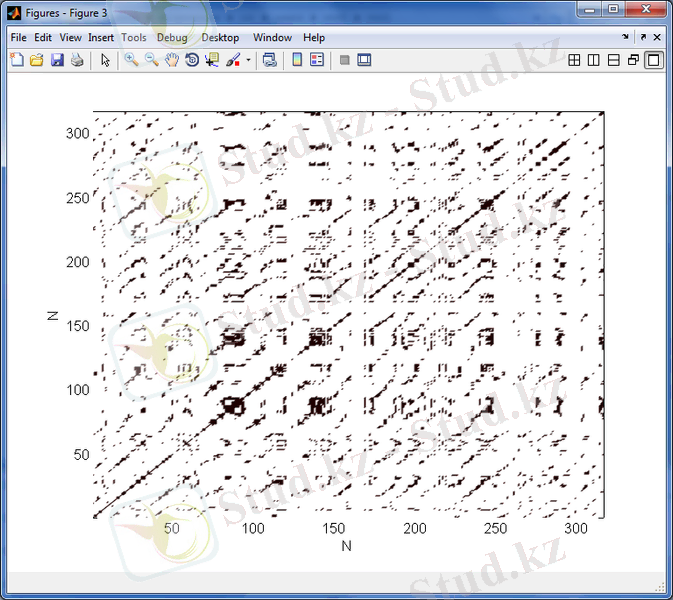
3. 24 сурет - 1975 - 1977 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

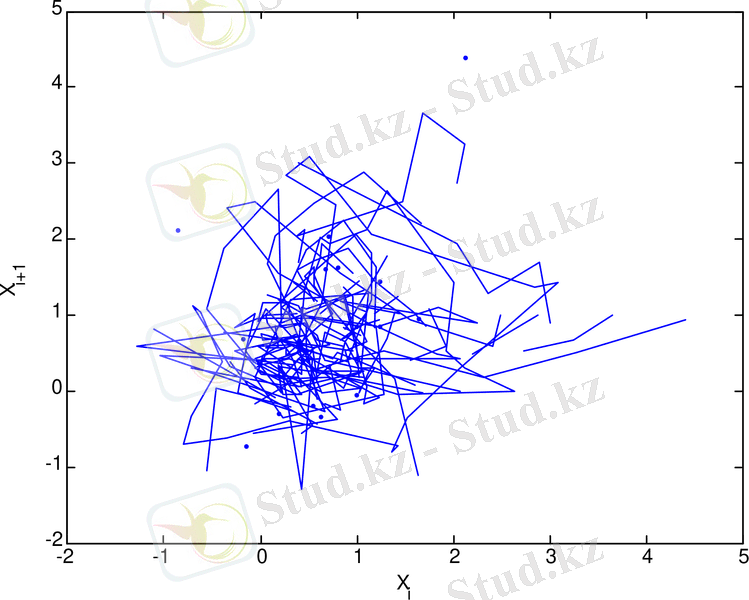
3. 25 сурет - 1975 - 1977 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің фазалық портреті

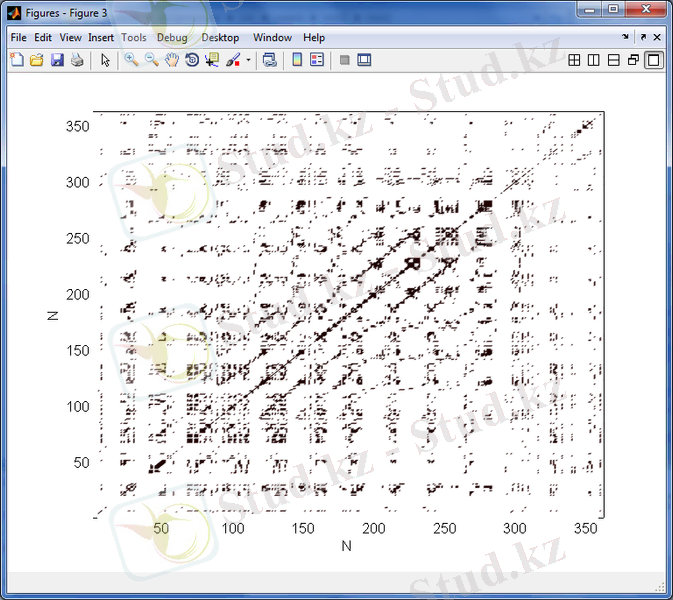
3. 26 сурет - 1985 - 1987 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

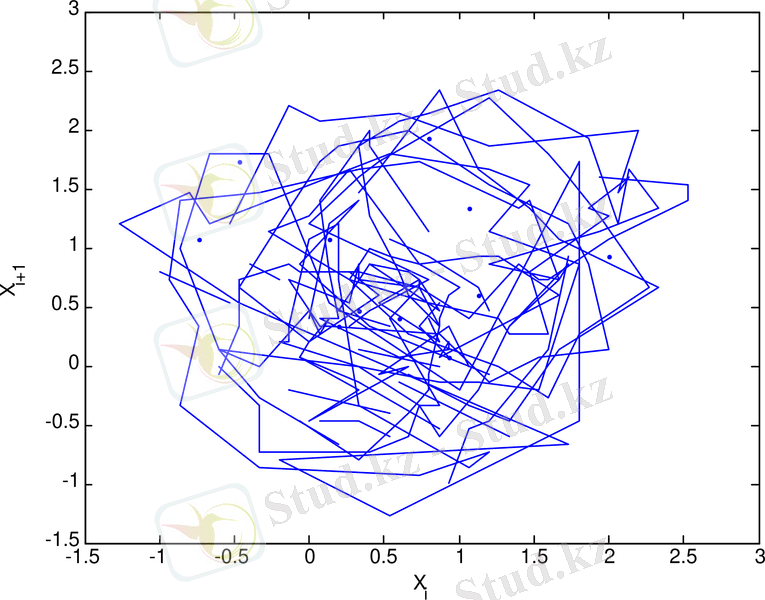
3. 27 сурет - 1985 - 1987 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің фазалық портреті

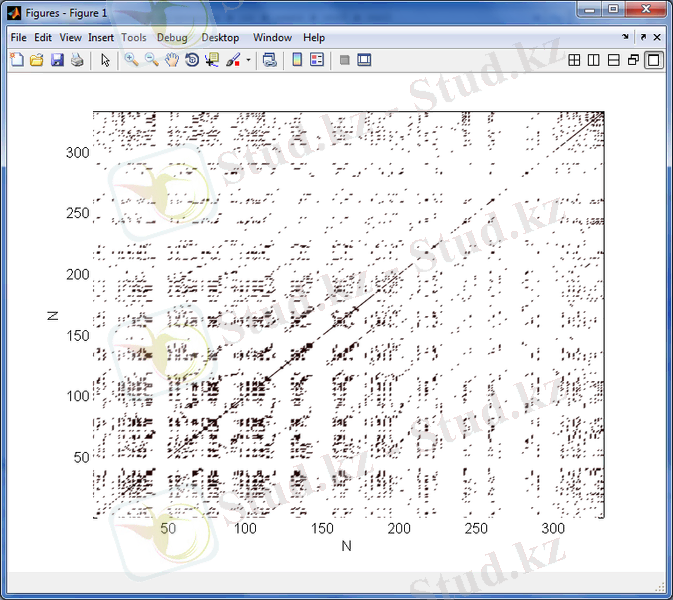
3. 28 сурет - 1995 - 1997 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің рекуренттік диаграммасы

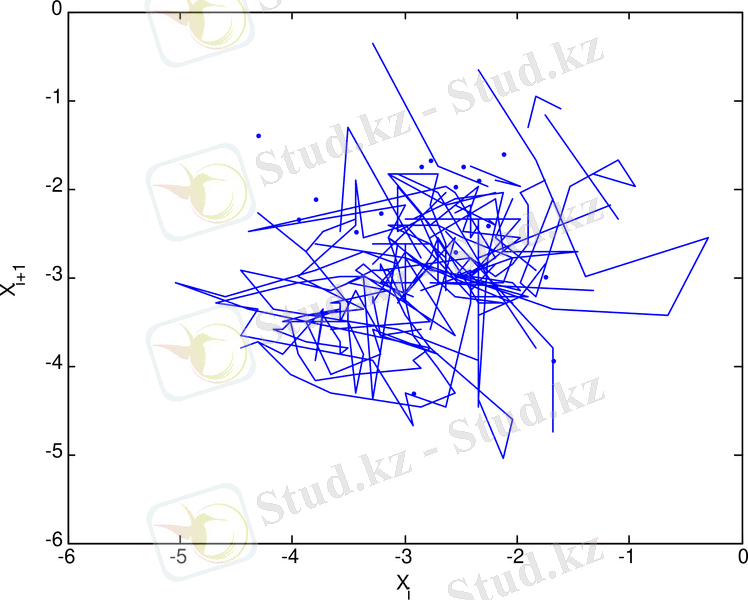
3. 29 сурет - 1995 - 1997 жж аралығындағы күн белсенділігінің минимумы кезіндегі орташа күн магнит өрісінің уақыттағы өзгерісінің фазалық портреті

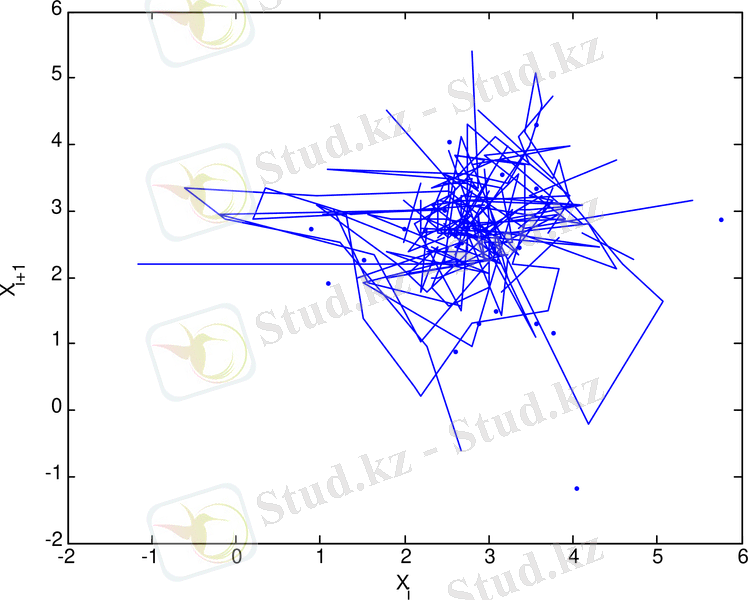
3. 18 - 3. 29 суреттерден келесіні көруге болады. Орташа Күн магнит өрісінің рекурренттік диаграммаларының құрылымы стохастикалық процестердікіндей сияқты біртекті емес, оларда хаостық процестерге тән нүктелер шоғырларынан тұратын түрлі құрылымдар, олар ішінде диагональ құрылымдары бақыланады, және де күн белсенділігінің минимумдері периодтарында бұл құрылымдар күн белсенділігінің максимумындарына қарағанда әлде-қайда анық көрінеді. Бұл айрмашылықты сандық түрде сипаттау үшін мынадай формула

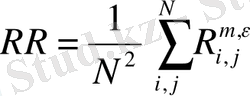(3. 1)

бойынша олардың рекурренттік өлшемі есептелді. Күн белсенділігінің максимумындары үшін бұл шама КБ минимумдеріндегіден көрі айтарлықтай (шамамен 30%) төмен болып шықты. Бұл Паккард -Таккенс әдісімен зерттеу нәтижесінде тұжырымдалған қорытындыға сәйкес келеді.

ҚОРЫТЫНДЫ

Жасалған жұмыстың негізгі кезеңдерін атап өтейік:

Күндегі жоғары энергиялы ірі ауқымды бейстационар процестерді зерттеу жөніндегі мәселенің қазіргі заманғы күйіне талдау жүргізілді.
Бейсызық физика шеңберінде дамытылған уақыттық қатарларды талдаудың жаңа әдістері, соның ішінде уақыттық тізбегі бойынша күрделі жүйелер динамикасын айқындаудың Таккенс әдісі, рекурренттік талдау әдісі игерілді.
WSO Wilcox Solar Observatory сайтында берілетін күн магнит өрістерінің уақыттағы өзгерісі туралы мәлімет алынып, оның алғашқы өндеуі жасалды.
Сәйкесінше уақыттық қатарлардың мультифракталдық қасиеттері күрделі жүйелер динамикасын айқындаудың Паккард-Таккенс әдісімен және рекурренттік талдау әдісімен талданды.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.