Күн белсенді аймақтарының токтық спиральдарының мультифракталды қасиеттері және скейлинг индекстерінің жарқылдарды болжаудағы маңызы


Күндегі белсенді аймақтардың мультифракталды қасиеттері
Ең алдымен күндегі белсенді аймақтардың фракталды қасиеттерін зерттеуге арналған Абраменконың бірнеше жұмыстарынан [19] шолу жасайық.
[20] -де Күндегі магнит өрісінің құйындық құрылымының фракталды талдау жасалған. Жалпы, Күндегі магнит өрісі фотосфераның астыңғы қабатында плазманың қозғалыс процесінде пайда болады. Плазма қозғалысы дегеніміз - Рейнольдс саны үлкен кезіндегі (дамыған турбуленттік ) турбуленттік қозғалыс, ол былай сипатталады: ол регулярлы емес, әрбір ағын нүктесінің жылдамдығы және уақыт бойынша ретсіз
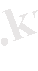 өзгеруі. Мұндай регулярлы емес жылдамдық өзгерісі бір нүктеден ағын нүктесіне дейінгі орынға ие, ол қазіргі уақытты қарастырылып отырғанымыздай. Толық теория бойынша дамыған турбуленттік қазіргі уақытта жоқ. Бірақ бір қатар маңызды нәтижелер анықталған. Бұл маңызды теория дамыған турбуленттегі ағын масштабтық каскад, яғни бұл Колмогорованың гипотезасы болып табылады. Бұл гипотеза бойынша турбуленттік ағындағы үлкен Рейнольдс санында құйынның барлық мөлшерлері бар. Үлкен құйындар кішкентай масштабтағы құйындарға таралып кетеді. Кез - келген l
v
мөлшерінен бастап көрейік, кішкентай құйындар тұтқырлық көмегімен диссипацияланады. Жүйеге түсетін энергиясы кішкентай құйынды каскадтарға беріледі. Колмогоров мынадай болжам жасады: барлық мынадай k (k=2
өзгеруі. Мұндай регулярлы емес жылдамдық өзгерісі бір нүктеден ағын нүктесіне дейінгі орынға ие, ол қазіргі уақытты қарастырылып отырғанымыздай. Толық теория бойынша дамыған турбуленттік қазіргі уақытта жоқ. Бірақ бір қатар маңызды нәтижелер анықталған. Бұл маңызды теория дамыған турбуленттегі ағын масштабтық каскад, яғни бұл Колмогорованың гипотезасы болып табылады. Бұл гипотеза бойынша турбуленттік ағындағы үлкен Рейнольдс санында құйынның барлық мөлшерлері бар. Үлкен құйындар кішкентай масштабтағы құйындарға таралып кетеді. Кез - келген l
v
мөлшерінен бастап көрейік, кішкентай құйындар тұтқырлық көмегімен диссипацияланады. Жүйеге түсетін энергиясы кішкентай құйынды каскадтарға беріледі. Колмогоров мынадай болжам жасады: барлық мынадай k (k=2
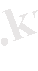 ) толқындық санға ие және толқындық санды K
0
шексіз үлкейтетін статистикалық сипатталатын қоздырылған жылдамдық, бұл өз кезгінде каскадтардағы энергия берілу жылдамдығы бағынады, ал k>k
v
тұтқырлыққа бағынады. Бұл болжаулар өлшемдік түсінік бойынша мынадай v
k
~k
-1/3
(v
k
-l
k
масштабындағы орташа флуктуация) толқындық сан интервалын
) толқындық санға ие және толқындық санды K
0
шексіз үлкейтетін статистикалық сипатталатын қоздырылған жылдамдық, бұл өз кезгінде каскадтардағы энергия берілу жылдамдығы бағынады, ал k>k
v
тұтқырлыққа бағынады. Бұл болжаулар өлшемдік түсінік бойынша мынадай v
k
~k
-1/3
(v
k
-l
k
масштабындағы орташа флуктуация) толқындық сан интервалын
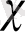 < k < k
v
< k < k
v
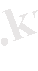 инерциялық интервалы деп атаймыз. Бұл инерциялық интервал қарастырылып отырған жүйенің маңызды характеристикасы болып табылады. (біздің жағдайымызда - жүйеде плазма плюс магнит өрісі бар ) : инерциялық интервал жүйе шегінде автомодельдеу (масштабты инвариант ) қасиетіне ие, немесе Мандельброт енгізген терминология бойынша жүйе фракталды құрылымға ие болады.
инерциялық интервалы деп атаймыз. Бұл инерциялық интервал қарастырылып отырған жүйенің маңызды характеристикасы болып табылады. (біздің жағдайымызда - жүйеде плазма плюс магнит өрісі бар ) : инерциялық интервал жүйе шегінде автомодельдеу (масштабты инвариант ) қасиетіне ие, немесе Мандельброт енгізген терминология бойынша жүйе фракталды құрылымға ие болады.
Жүйенің фракталды сипаты мынадай мүмкіншіліктерді береді. Біріншіден, жүйедегі энергия спектр бойынша үлкен масштабтан кіші масштабқа және, керісінше, кіші масштабтан үлкен масштабтарға беріле алады деген қорытындыны жасауға болады. Ақырында күндегі плазмаға өте маңызды, ол Зеехаферамның магнит өрісі кіші масштабты флуктуация энергия тасымалдау механизмін және күн атмосферасының жылдамдығы үлкен масштабты коронадағы орталық өріс энергиясы тасымалданады деген ұсынысын жоққа шығара алмайды. Екіншіден, жүйенің фракталды параметрлері - жүйенің организациялық құрылымын береді. Сондықтан бұлардың өзгерісі белсенді жарқылға байланысты генерациядағы жарқыл проблемасын түсіндірер еді. Үшіншіден, соңғы жылдары фракталды жүйенің математикалық аппарат анализ жасау компьютер модель жасауға мүмкіншілік береді.
Белсенді облысы магнит өрісінің спиралі фракталды қасиетін түсіну үшін Абраменко күндегі магнит өрісінің векторын қолданды, ол Пекиндік астроном обсерваториядағы күндік SMFT телескобымен жүргізілді. Тәжербие фотосфера түзетін Fe І 5324, 19
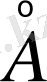 спектірлік сызық жүргізіледі. Телескоптың көру өрісі - 218’’x314” (ПЗС матрица 512х512 ұяшық) .
спектірлік сызық жүргізіледі. Телескоптың көру өрісі - 218’’x314” (ПЗС матрица 512х512 ұяшық) .
Тегістеуден кейін магнитограмма ұяшығы 1, 72 “1, 72х1, 86” болса, магнитограмманың размері 128х170 ұяшықты құрайды. Әрбір магнитограмманың проектысы эффект құрылған, өріс векторы координатта жүйесінде, Z осі магнитограмма центрінен күнге дейінгі беттін нормаліна сәйкес.
Біз белгілеген бір көлемде күн атмосфера өріс векторы жайлы ақпарат бере алмаймыз, бірақ біз фотосферамен бір бірдей өріс векторы ие бола аламыз. Сондықтан біз фотосферадағы өріс токтарының спиралі тек кішкені бөлігіне ғана шығара аламыз.
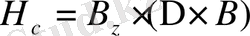 (1. 21)
(1. 21)
есептеуге
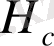 берілген алгаритм қолданған (жабық контур токта магнитограмма бір әлем ұяшығын береді, мынаны емес 5×5 ұяшық) .
берілген алгаритм қолданған (жабық контур токта магнитограмма бір әлем ұяшығын береді, мынаны емес 5×5 ұяшық) .
Токтық спирал карта
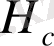 2 өлшемді сеткасы 128×170 бұл өріс тоғын спирал инварианттық масштабтың қасиетін пайдаланады.
2 өлшемді сеткасы 128×170 бұл өріс тоғын спирал инварианттық масштабтың қасиетін пайдаланады.
[21] 2 өлшемінде өзгермелі белгі құрлымына
 Скейлинг алгариитм берілген. Ол белгі өлшемдеріне маңыздылығы
Скейлинг алгариитм берілген. Ол белгі өлшемдеріне маңыздылығы
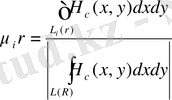 (1. 22)
(1. 22)
мұнда
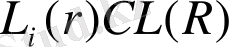 қиылыспайтын иеархиялық размері r квадрат болып табылады. L барлық квадраттарды жабады, размері R×R ұяшық, бұл активті облыстарды қоршайды. Бірінші кезде Скейлинг өзгерістерінің белгісінің қасиетін былай оқуды ұсынды.
қиылыспайтын иеархиялық размері r квадрат болып табылады. L барлық квадраттарды жабады, размері R×R ұяшық, бұл активті облыстарды қоршайды. Бірінші кезде Скейлинг өзгерістерінің белгісінің қасиетін былай оқуды ұсынды.
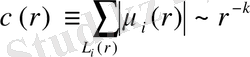 (1. 23)
(1. 23)
егер қарастырылып жатқан таңбаларның ауыспалы қасиеттерінің белгілерін интервал масштабтарында не болса, онда біз
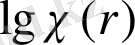 және
және
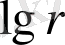 арасындағы сыртқы тәуелділікті күтуге болады. r-дің R үлесі деп алайық, онда спектрді мынамен есептеуге болады
арасындағы сыртқы тәуелділікті күтуге болады. r-дің R үлесі деп алайық, онда спектрді мынамен есептеуге болады
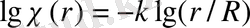 (1. 24)
(1. 24)
барлық есептеулер
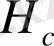 пен және
пен және
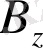 параллель жүргізілді, K
h
ток спираль өрісінің көрсеткіші, ал K
В
өрістің вертикаль құраушылары. K
h
пен K
В
коэффициетріне R
j
≡R кв. Алынып былай болды. Біз картадан N кв. қатарын L(R) деп таңдап алдық, өйткені маңызды
мах
өрісте кв. Жағы қиылыспауы тиіс. (Н
с
қандай болса В
z
-де солай) онда әлсіз өріс тік болады. Әрбір спектрлерге жақсы визуальды сызықтық участок таңдалған және соның шегінде аудан кішкентай кв. әдісі бойынша мынадай коэффицент анықталды. К
h
(l) немесе K
B
, l=I
m
N. N
параллель жүргізілді, K
h
ток спираль өрісінің көрсеткіші, ал K
В
өрістің вертикаль құраушылары. K
h
пен K
В
коэффициетріне R
j
≡R кв. Алынып былай болды. Біз картадан N кв. қатарын L(R) деп таңдап алдық, өйткені маңызды
мах
өрісте кв. Жағы қиылыспауы тиіс. (Н
с
қандай болса В
z
-де солай) онда әлсіз өріс тік болады. Әрбір спектрлерге жақсы визуальды сызықтық участок таңдалған және соның шегінде аудан кішкентай кв. әдісі бойынша мынадай коэффицент анықталды. К
h
(l) немесе K
B
, l=I
m
N. N
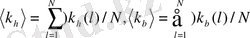 (1. 25)
(1. 25)
Одан басқа N спиралдары орташалану жүргізіледі және орташаквадрат ауытқу
 шамасы есептелді.
шамасы есептелді.
Одан басқа N спек Lm орташалау жүргізілді. Және орташа квадратқа ауытқту Шамасын есептелінеді. Lg k (ri), i=1… m. Ары қарай орташа спектр көрсетілген. Визуальды орташа спекторы жақсы сызықтардан алынады. Және сол бойынша ең кіші кв әдісі бойынша n спектр накион есептелінеді. Бұл әдіс бойынша есептелген Kn және Kb коэффициенті (Kn) және (Kb) осындай коэффиценті қателігінің шегінде болады. Қайта оқытылуы әлсіз өрістегі Hc жане B зоналардағы сәйкестік қайта қарау мынаны көрсетеді. (Kn) және (Kb) спектор көрсеткіштері размер мен орыналасу кв. L(R) әлсіз өріс зоналарды тіптерде сондықтан биполярлы белсенді облысы бірінші және соңғы бөліктерін бөлек -бөлек есептелінеді. АО ыңғайлы,
 -конфигурациясы сияқты, жалғыз ғана дақтар мен кішкентай биполярлы облыс бір ғана квадрат L(R) ұстап алып және оны толық қарастыра алатын болдық.
-конфигурациясы сияқты, жалғыз ғана дақтар мен кішкентай биполярлы облыс бір ғана квадрат L(R) ұстап алып және оны толық қарастыра алатын болдық.
Кейбір белсенді аймақтар үшін өріс спиральдігінің спектрлері 1. 8 суретте көрсетілген. Ауқымда биполярлы АО-да ток спирлі Скейлинг қасиеті әр жерде әртүрлі бола алады. АО заң бойынша К
һ
көрсеткіш АО-ғы бірінші бөлігі слңғы бөлііне қарағанды аз. Бұл былай түсіндіріледі: лидер (1-ші) магниттік өріс монолитно өрістелген соңғыға қарағанда. Бұл факт токтың спин өрісіне әсер етеді.
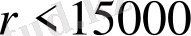 км ескерсек ток спиралінің сызығы спектр мықты дәрежеде ұсталынып тұрады:
км ескерсек ток спиралінің сызығы спектр мықты дәрежеде ұсталынып тұрады:
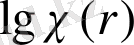 және
және
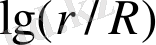 арасында корреляция 0, 90 индивидуальдық спектр көп.
арасында корреляция 0, 90 индивидуальдық спектр көп.
Барлық ток спектрлері үшін алынған спектр түрлері сызықтық спектрі кішкентай r -ге жалғаса береді. Қандай жағдайда болсын магниттік өріс тоқ спектріне 1000-15000 км шк. инверв. масштаб инварианттардың қасиетеріне ие. Бұл инвариант шкалалар кезкелген ауданда ток спиралі даминделетін орын бар.
Спектр сызықтығы аудан спектріне ашық жатқан жерде энергия тасымал алады, ол үлкен масштаб кіші масштабқа (тік (оң) каскад) немесе кішіден үлкен каск. тері каскад) . Спектр энергия тасым механика бір мүмкіншілігі жүйедегі плазма - магнит өрісі. Бұл қосымша ЭДС генераця альфа эффектісі деп аталатын. Зихафа [22] мынаны көрсетеді: альфа эффект жұмыс істеу шарты мынадай -Күн атмосфера көлемінде -обьемда тоқ спираль өрісі нолдік емес разбалансқа.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz