Радиофизика есептерін шешуде бейсызық физика әдістерін қолдану: Ван-дер-Поль, Анищенко-Астахов және инерциялық генераторлардың фазалық және фракталдық талдауы


Жүйенің фазалық кеңістігінде оқшауланған тұйық траекториямен бейнеленетін, бастапқы шартқа тәуелсіз, біраз уақыттан кейін кейбір қашықтықтағы траекториялары тартылатын периодты, асимптотты орнықты қозғалыстың болу мүмкіншілігі тек бейсызықты диссипативті жүйелерде ғана қамтамасыз етіледі. Динамикалық жүйенің тербелмелі процестерін зерттегенге қажет болғаны соншалық, А. А. Андронов бұл типке арнайы термин - автотербелмелі жүйе деген ұғым енгізді.
Динамикалық жүйенің мысалы ретінде Пуанкаренің шекті циклімен сипатталатын классикалық бейсызық Ван-дер-Поль осцилляторын қарастырамыз. 4-суретте Ван-дер-Поль генераторының принциптік сүлбесі келтірілген.
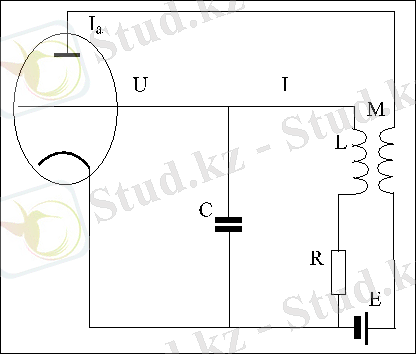
12-сурет. Тор тізбегіне жалғасқан тербелмелі контурлы
Ван-дер-Поль генераторының принциптік схемасы
Алдымен, осы генератордағы автотербелістің туу жағдайын сапалық түрде сипаттаймыз. LC контурда пайда болған шағын тербелістер тор арқылы U кернеуді периодты басқарады. Пайда болған анодты ток ( I a ) өздік индукциямен ( M ) қамтамасыз етілген оң кері байланыс арқылы осы тербелістерді күшейтеді.
Тербелістің амплитудасының өсуінің қанығуы болады және контурға енгізген энергия сол контурдағы энергияның жойылуымен шамалас, сондықтан одан ары амплитуданың өсуі тоқтатылады.
Біз Ван-дер-Поль теңдеуін сандық модельдеуге ыңғайлы мына түрде қарастырамыз:
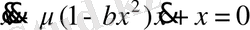 . (48)
. (48)
Төменде
VDP. m
файл-функцияның және «Ван-дер-Поль осцилляторы» атты программаның MatLab тілінде жазылған листинг келтірілген, мұнда (17) -теңдеу параметр
μ
= 1 болғанда шешілген.
х
(
t
) және
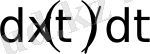 үшін жазылған бастапқы шарттар сияқты, бұл параметр шешімнің сипатын анықтайды.
μ
оң болғанда жүйедегі тербеліс ұлғаяды, бірақ жүйе бейсызық болғандықтан, олардың амплитудасы шектеулі, ал формасының синусоидадан ерекше екені көрініп тұр (7
a
-сурет) . Шекті цикл (7
б
-сурет) - ол фазалық жазықтықтағы қай нүктеде болмасын, өзіне траекторияны тартатын ауқымды, орнықты жекеленген құрылым.
үшін жазылған бастапқы шарттар сияқты, бұл параметр шешімнің сипатын анықтайды.
μ
оң болғанда жүйедегі тербеліс ұлғаяды, бірақ жүйе бейсызық болғандықтан, олардың амплитудасы шектеулі, ал формасының синусоидадан ерекше екені көрініп тұр (7
a
-сурет) . Шекті цикл (7
б
-сурет) - ол фазалық жазықтықтағы қай нүктеде болмасын, өзіне траекторияны тартатын ауқымды, орнықты жекеленген құрылым.
a б
15-сурет. (17) - теңдеудің шешімі мен шекті циклі
a ) μ = 1, b = 1; б ) μ = 1, b = 0. 5
Шекті цикл
mu=1 үшін Ван-дер-Поль теңдеуінің шешімі
Y
T
Сонымен, тербеліс жасайтын айнымалыдан энергия диссипациясы бейсызық байланыста болатын динамикалық жүйеде, ең алдымен, фазалық траекториялардың орнықты шектелген жиындарының принциптік жаңа түрі пайда болды: ол - шекті цикл. Шекті циклдегі қозғалыс автотербелмелі жүйеде болатын уақыт бойынша энергия өзгерісінің күрделі процесін көрсетеді. Егер сыртқы ұйытқу арқылы фазалық жазықтықтағы траектория шекті циклдің ішіне ығысса, онда енгізілген энергия орта есеппен шашыраған энергиядан артық. Дивергенцияның орта мәні мұнда оң болады. Әр түрлі тербеліс жүйелерінің дивергенциясының анықтамасы туралы түсініктемелер төменде «Тапсырмалар» бөлігінде келтірілген. Шекті циклдің сыртында дивергенция теріс, фазалық траекториялар шекті циклдан сыртқа ұмтылады.
Сыртқы гармониялық ұйытқуды ескергендегі (амплитудасы
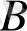 ) және кері байланыс коэффициенті (теріс кедергі)
) және кері байланыс коэффициенті (теріс кедергі)
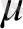 , бейсызық тербелістер жиілігі
, бейсызық тербелістер жиілігі
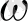 болатын Ван-дер-Поль теңдеуі мына түрде жазылады:
болатын Ван-дер-Поль теңдеуі мына түрде жазылады:
 . (49)
. (49)
8
а
,
б
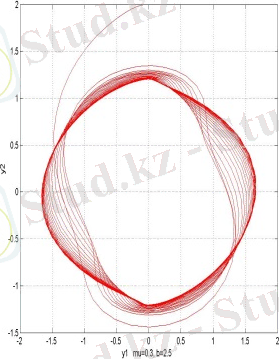
- суреттерде әр-түрлі
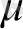 ,
,
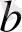 ,
,
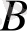 ,
,
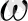 үшін (18) теңдеудің фазалық траекториялары көрсетілген.
үшін (18) теңдеудің фазалық траекториялары көрсетілген.

Ван-дер-Поль генераторы сияқты жүйелерден басқа автономды жүйелерге туннельді диодтан тұратын тербелістер генераторы және көптеген синусоидалы және релаксациялық, соның ішінде электронды лампа мен өрістік транзисторлармен құрылған автогенераторлар кіреді.
2. 2 Анищенко-Астаховтың инерциялық бейсызық генераторы
Бұл қүбылыс бірқатар физикалық жүйелерде және сандық модельдеумен анықталған.
10-суретте Анищенко-Астаховтың инерциялық бейсызық генераторында (ИБГ) келесі теңдеулер арқылы
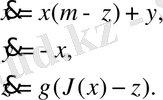 (50)
(50)
кезекті еселенуі арқылы хаосқа өту процесіндегі өзгерістерді көре аламыз.
Бұл ауысу бірпараметрлі талдау жасауға мүмкіндік береді (өйткені екі еселену бифуркациясының өлшемділігі бірге тең) . Басқару параметрінің m = m 0 белгілі бір мәнінде динамикалық жүйенің Т ( m ) периодты С орнықты циклы бар болсын. Параметрдің мәні m = m 1 дейін ұлғайған кезде периодтың екі еселену “суперкүдікті” бифуркациясы жүрсін, ол периоды 2Т ( m ) -ге тең орнықты шекті 2 С циклын тудырсын. Әрі қарай m = m k , k = 1, 2, 3, . . . нүктелерінде 2 k С циклдардың периодтың екі еселену бифуркациясының шексіз тізбегі жүреді. Спектрде ω 0 =2π/Т 0 жиілікті субгармониктер түзіледі, сондықтан екі еселену бифуркация тізбегін кейде субгармоникалық каскад деп атайды. m k бифуркациялық нүктелер k → ∞ шегінде кейбір m = m cr шекті шамаға жинақталады, сол кезде период шексіз, ал спектр біртұтас болып келеді. m > m cr кезінде апериодты тербелістер байқалады, Ляпунов бойынша орнықсыз болады (Ляпунов көрсеткіштері келесі тақырыпта қарастырылған) . Бұл тербеліске фазалық кеңістік жүйесінде әуейі аттрактор сәйкес келеді.
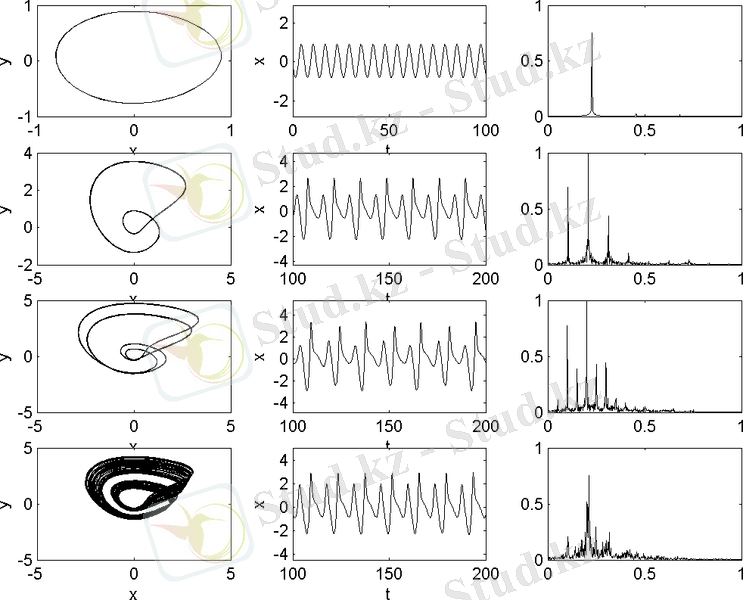
17-сурет. ИБГ периодтың екі еселену бифуркациясының тізбегі
а ) фазалық траекторияның проекциялары , б ) тербеліс пішіндері және
в ) 2 Т 0 k , к = 1, 2, 3 периодты цикл және әуейі аттрактор үшін қуат спектрлері
2. 3 Параметрлері флуктуацияланатын автотербелмелі жүйе
Мысал ретінде реалды физикалық процестің фракталды қисықтарын қарастырайық. 20
а
-суретте параметрлері флуктуацияланатын автотербелмелі жүйенің теңдеуінен алынған, ұзақтығы бірдей сигналдар үшін
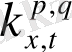 мәнінің уақыт өсімен қиылысу санына (
ν
) тәуелділік қисығы көрсетілген
мәнінің уақыт өсімен қиылысу санына (
ν
) тәуелділік қисығы көрсетілген

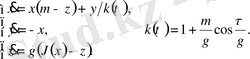 (51)
(51)
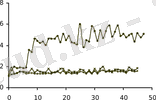 Сигналдың формасы және соған орай фазалық суреті 20
б
, 20
в
суреттерінде көсетілген.
Сигналдың формасы және соған орай фазалық суреті 20
б
, 20
в
суреттерінде көсетілген.
20-суретте параметрлері флуктуациялы генератор сигналдарының (15) формула бойынша есептелген фракталдық өлшемділіктері көрсетілген.
(23) теңдеулер жүйесі
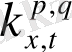 мәні үлкен және әуейі, хаосты аттракторлы режимдегі параметрлерінің флуктуациясы бар автотербелмелі жүйені сипаттайды. Параметрлер флуктуациясын ескеру күрделі құрылымды сигналдарды (
g
> 1) алуға және импульстердің масштабты инвариантты (фракталды) қасиеттерін бақылауға мүмкіндік береді. Фракталдық заңдылықтарды, яғни зерттеуде сигналдардың ішкі құрылымын ескермесек, біз сигналдың заңдылығын білу үшін стационар емес көп уақытқа тәуелді жағдайды қарастыруымыз қажет.
мәні үлкен және әуейі, хаосты аттракторлы режимдегі параметрлерінің флуктуациясы бар автотербелмелі жүйені сипаттайды. Параметрлер флуктуациясын ескеру күрделі құрылымды сигналдарды (
g
> 1) алуға және импульстердің масштабты инвариантты (фракталды) қасиеттерін бақылауға мүмкіндік береді. Фракталдық заңдылықтарды, яғни зерттеуде сигналдардың ішкі құрылымын ескермесек, біз сигналдың заңдылығын білу үшін стационар емес көп уақытқа тәуелді жағдайды қарастыруымыз қажет.
(15) өрнек өзаффинді, өзұқсас D * 1 және D * 2 екі кризистік фракталды өлшемділікті анықтайтындығы 6 суреттен көрінеді. Жоғарғы дәлдікте ( δ<δ * 1 ) D * 1 ≠ D * 2 қисықтың өзаффинділігі байқалады. Жазықтықтың өзаффинділігі керісінше, өлшеудің сызықтық масштабы үлкен ( δ>δ * 2 ) болғанда байқалады.
Өлшеудің кризистік δ * масштабының салыстырмалы үлкен мәндерінде фракталдық өлшемділіктің кризистік мәндері D *1 , D *2 тұрақты болады (7-сурет) .
δ *
D *1 , D *2
21 - сурет. m = 1. 5 және g = 4. 5 параметрлері үшін фракталдық D 1, 2 өлшемділіктің өлшеу масштабына ( δ) тәуелділігі. L және F (16), (17) интегралы арқылы есептелінген.
D 1, 2
D * 2
D * 1
δ * 2
δ * 1
δ
22-сурет. D * 1 , D * 2 кризистік фракталдық өлшемділіктің δ * кризистік масштабқа тәуелділігі.
Өзаффинді қисықтан өзұқсас қисықтың айырмашылығы және жоғарыда айтылған әдістерді қолдану қажетілігі 23-суретте анық көрсетілген.
1. 5 2 2. 5 3 3. 5 4 k 2
D- 1
1. 4
1. 2
1. 0
0. 8
23-сурет. Автотербелмелі жүйе үшін фракталдық өлшемділіктің (19) -формула бойынша есептелген k 2 -ге тәуелділігі.
× - D 1 -1, + - D 2 -1, ● - (2) -формула бойынша есептелген фракталдық өлшемділік.
Параметрлері флуктуациялы автотербелмелі жүйенің теңдеулер жүйесінен алынған сигналдар үшін
 форма коэффициенті мен скейлинг көрсеткіші арасындағы тәуелділік 10-суретте көрсетілген. Түрлі формалы қисықтардың фракталдық өлшемділігі өзұқсас максималды
форма коэффициенті мен скейлинг көрсеткіші арасындағы тәуелділік 10-суретте көрсетілген. Түрлі формалы қисықтардың фракталдық өлшемділігі өзұқсас максималды
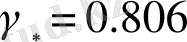 , ал бірлік радиусты фракталдық сфера үшін минималды
, ал бірлік радиусты фракталдық сфера үшін минималды
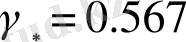 мәніне ие
мәніне ие
Инерциялы бейсызық генератор.
24-суретте төмендегі теңдеулер жүйесімен сипатталатын инерциялы бейсызық генератордан алынған сигнал түрі көрсетілген [16] :
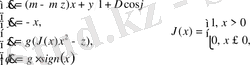 (52) ,
(52) ,
мұндағы
x, y, z
- тербелмелі контурдың шығыс кернеулері,
m
,
g
- сәйкесінше қозу және инерциялық параметрлері,
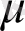 - бейсызық түрлендіргіш пен тербелмелі контурдың шығыс кернеулерін үйлестіру параметрі,
D,
- бейсызық түрлендіргіш пен тербелмелі контурдың шығыс кернеулерін үйлестіру параметрі,
D,
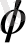 - шуыл флуктуациясының интенсивтілігі мен фазасы.
- шуыл флуктуациясының интенсивтілігі мен фазасы.
24-Сурет.
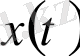 - сигнал түрі
- сигнал түрі
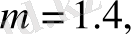
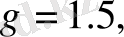
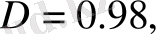
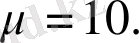
25-суретте жоғарыда аталған генератордан алынған сигнал үшін фазалық сурет тұрғызылған.
25-сурет. Тербелістердің фазалық суреті
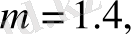
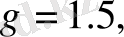
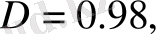
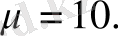
26-суретте
 -Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
-Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
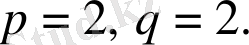
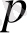 және
және
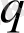 параметлерінің шамасын мына шарт орындалатындай етіп таңдаймыз:
параметлерінің шамасын мына шарт орындалатындай етіп таңдаймыз:
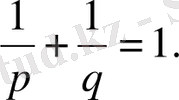
26-сурет.
 -Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
-Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
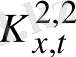 .
.
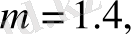
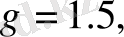
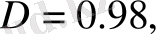
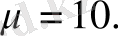
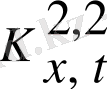
26-суреттен радиофизикалық сигналдардың фракталдық өлшемдері өзұқсас жағдайында
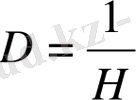 өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
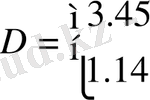 .
.
27-суретте (52) теңдеулер жүйесімен сипатталатын генератордан алынған сигнал параметрлері өзгертіліп көрсетілген.
27-сурет
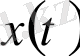 сигнал түрі
сигнал түрі
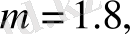
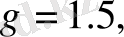
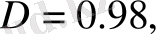
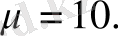
28-суретте жоғарыда аталған генератордан алынған сигнал үшін фазалық сурет тұрғызылған.
28-сурет. Тербелістердің фазалық суреті
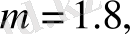
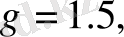
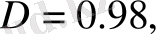
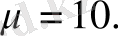
29-суретте
 -Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
-Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
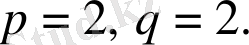
29-сурет.
 -Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
-Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
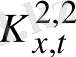 .
.
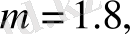
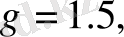
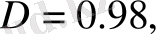
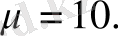
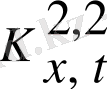
29-суреттен радиофизикалық сигналдардың фракталдық өлшемдері өзұқсас жағдайында
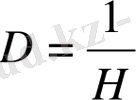 өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
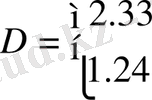 .
.
30-суретте (52) теңдеулер жүйесімен сипатталатын генератордан сигнал төмендегі параметрлерге сәйкес алынған.
30-сурет
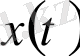 сигнал түрі
сигнал түрі
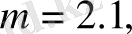
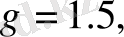
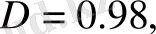
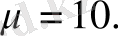
31-суретте жоғарыда аталған генератордан алынған сигнал үшін фазалық сурет тұрғызылған
31-сурет. Тербелістердің фазалық суреті
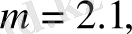
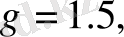
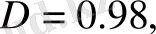
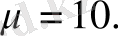
32-суретте
 -Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
-Херст көрсеткішінің аффиндік коэффициенттен тәуелділігі көрсетілген. Есептеулер (47) өрнекке сәйкес жүргізілген және ондағы тұрақты шамалар былайша анықталған
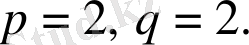
32-сурет.
 -Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
-Херст көрсеткішінің аффиндік коэффициентінен тәуелділігі
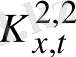 .
.
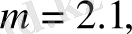
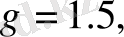
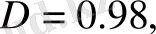
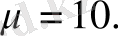
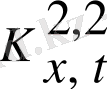
32-суреттен радиофизикалық сигналдардың фракталдық өлшемдері өзұқсас жағдайында
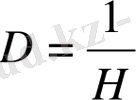 өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
өрнегі арқылы үйлесетіндігін көруге болады, ол
D-
ның мынадай мәндерінде жүзеге асады:
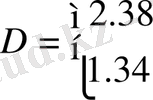 .
.
Қорытынды
Дипломдық жұмыстың мақсаты әр түрлі радиосигналдарды бейсызық физиканың әдістері көмегімен сипаттауға болатындығын көрсету еді. Жасалынған жұмыстар:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz