Сигналдардың вейвлет-талдауы: теориясы, үздіксіз вейвлет-түрлендіру және қолданбалары


РЕФЕРАТ
Сигналдардың вейвлет-талдауы
Жергілікті ерекшеліктері бар сигналдардың бірдей талдануы үшін өте ыңғайлы құрал вейвлет-түрлендіру болып шықты, өйткені оның негізінің (вейвлетінің) элементтері уақыттың, жиіліктік облыстарда жақсы шектелген және қозғалмалы жиілікті-уақыттық терезеге ие. Осылайша, вейвлеттің ашылуы, бүкіл көрініс бойынша, аса қиын және өзекті ғылыми қиыншылықты шешті. Бұл шешімнің негізгі функциялар мен сигналдардың - оған қоса бейстационарлы декомпозиция (бөліну) мен реконструкция (қайта қалыптасу, сүзулер) үшін қолданылатын функциялар класы мен жаңа негізді түбегейлі өңдеу болды. Сәйкесінше функциялар мен сигналдарды көрсететін жаңа қондырғы, ал мүлдем жақында оны іске асуы үшін қажет құралды және бағдарламалы амалдар құрылған.
Қазіргі уақытта вейвлет деп аталған анализаторлар тобы бейнелерді тану әдістерінде; мысалы, сөйлеу сияқты әртүрлі сигналдардың синтезі мен өңдеу кезінде; әртүрлі табиғаттың бейнелерін (бұл көздің құбылмалы қабаты, бүйректің рентгенограммасы, планеталардың беттері мен бұлттардың серіктес бейнелері, минералдың суреті, және т. б. болуы мүмкін) талдау үшін; турбулентті өрістердің қасиеттерін игеру үшін; үлкен көлемді хабарларды бұрау (жинау) үшін және көптеген басқа жағдайларда кең қолданыла бастады.
Вейвлеттерді пайдалану облысы тәжірибеде немесе бақылау кезінде сандық алынған табиғаты әртүрлі сигналдар мен өрістердің қасиеттерін талдаумен шектеліп қоймайды. Вейвлеттер кеңістіктік және уақыттық жиіліктің кең диапазонында ұйытқулардың әсерлесуімен сипатталатын, күрделі бейсызықты құбылыстардың динамикасын сипаттау үшін жақсы бейімделген иерархиялық базис сияқты тікелей сандық моделдеу үшін қолданыла бастады.
Вейвлет-талдау кезектесумен құбылыстарды талдау үшін өте ыңғайлы болып шықты. Ол меңгерілетін заттың кеңістіктік таралған қасиеттерін айқындауға, кезектесудің бар болуын және диссипациялар облыстарының таралуын анықтауға, зат туралы жергілікті жоғары жиіліктік және ғаламдық үлкен масштабты хабарды алуға және көптеген жеткілікті дәл және артықшылығы жоқ хабарларды алуға мүмкіндік береді.
Көптеген зерттеушілер вейвлет-талдауды “математикалық микроскоп” деп атауы тегін емес - атау әртүрлі масштабтарда жақсы рұқсатта әдістің керемет қасиетін сақтауды тамаша шағылдырады. Бұл “микроскоптың” маңызды біртекті емес заттың ішкі құрылымын және көптеген, дербес жағдайда фракталды Вейерштрасс функциялары мен канторлы қатарлардың ықтималды өлшемдері сияқты классикалық мысалдарда көрсетілген оның жергілікті скейлингті қасиеттерін меңгеруді айқындау мүмкіншілігі болып табылады. Вейвлет-талдаудың Рейнольдс сандары үлкен кезде желдік туннельде турбулентті өрістің жылдамдығына қолданылуы алғашқыда Ричардсон сарқырамасының бар болуының дәлелдеуін берді. Энергетикалық сарқырамалы құбылыстардың мультифракталды біртекті емес канторлы сарқырамалардың құрылымымен ұқсастығы көрсетілген. Аса әсерлі болып вейвлет-талдауды диссипативті жүйелерде жағдайлардың хаосқа өту бақылауларын өзгертетін, кейбір жақсы танымал динамикалық жүйелердің мультифракталды инвариантты өлшемдерге қолдануы шықты.
2. 1. Вейвлет-түрлендірудің идеясы
Сигналдардың вейвлет-түрлендіруі бүгін жалпы қабылданған
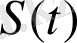 сигналдардың талдауына жақындауға - оларды
сигналдардың талдауына жақындауға - оларды
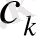 коэффциенттерге көбейтілген
коэффциенттерге көбейтілген
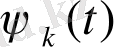 базисті функциялардың жай құраушыларының өлшенген қосындысы түрінде көрініске негізделген
базисті функциялардың жай құраушыларының өлшенген қосындысы түрінде көрініске негізделген
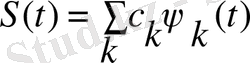 . (2. 1)
. (2. 1)
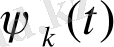 базисті функциялар толығымен анықталған түрдегі функциялар сияқты берілген деп жорамалданса, онда тек
базисті функциялар толығымен анықталған түрдегі функциялар сияқты берілген деп жорамалданса, онда тек
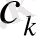 коэффициенттер құрамында нақты сигнал туралы хабарға ие. Осылайша, әртүрлі базисті функциялармен (2. 1) қатарлар негізінде дербес сигналдардың көріну мүмкіншіліктері туралы айтуға болады.
коэффициенттер құрамында нақты сигнал туралы хабарға ие. Осылайша, әртүрлі базисті функциялармен (2. 1) қатарлар негізінде дербес сигналдардың көріну мүмкіншіліктері туралы айтуға болады.
Мысалы, Фурье қатарлары базисті функциялары ретінде комплексті экспонентамен көрсетілген синусоидалар мен косинусоидаларды пайдаланады. Олар вертикаль сызыққа (дельта-импульс) жиіліктік облыста (спектрограммада пайда бола отырып) шекті шоғырланады, бірақ уақыттық облыста өте нашар шоғырланған (дәлірек айтсақ, мүлдем шоғырланбаған) .
Дәл қарама-қарсы мысал - импульсті функция (Кронекер функциясы)
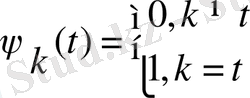 .
.
Ол уақытта нақты шоғырланған және сондықтан сигналдың бөлінулерінің көріністері үшін келеді, бірақ сигналдың жиілігі туралы ешқандай хабар алып жүрмейді және сондықтан сигналдардың және периодты сигналдардың уақытының берілген кесіндісінде аз өзгеретін көріністер үшін нашар бейімделген. Дәл осы кемшілік сигналдардың және Тейлор қатарынан Фурье қатарларына дейінгі функциялардың аппроксимациялануының басқа әдістерінде болған.
Бірсыпыра бөлек Габор түрлендіруі тұр. Онда базисті функция ретінде Гаусс терезесі (1 гауссиан) арқылы өткізілген синусоида қолданылады. Бұндай функциялар жиілік бойынша да, уақыт бойынша да шоғырланған бола алады. Дегенмен, олар негізінде ортогональ емес және сигналдардың жергілікті ерекшеліктерін көрсететін бөлігіндегі синусоиданың кемшіліктерін мұраланады. Бұл кезде талдау функциялары нашар ескертілген болады, ол түрлендіру кезінде үлкен қателерге әкеледі, олардың нәтижелері барлық жиілік бойынша сияқты, кеңістіктегі облыстарда “жағылады”.
Осылайша, көрсетілген кемшіліктерден бос, функциялар мен сигналдардың талдауға жаңа математикалық аппаратты құруға өткір қажеттілік жетілді. Олар болып вейвлеттер мен вейвлет-түрлендірулер шықты.
Сейсмикалық акустикалық сигналдардың талдауымен байланысты 80-ші жылдардың ортасында Гроссман және Морлимен (J. Morlet) алғаш енгізілген вейвлет термині ағылшынның wavelet сөзінен аударғанда “қысқа (немесе кішкентай) толқын” дегенді білдіреді. Бізде оны басында “шолпу”, “лақтырылу” және т. б. нұсқаларменен аударған, ол сәтсіз болды, өйткені көптеген вейвлеттер жарық айқындалған тербелмелі компонетасы (толқындар сияқты) бар уақыттық тәуелділікке ие. “Шолпу” және “лақтырылу” сөздері вейвлеттердің осцилляциялау дәлелін айқындамайды. Вейвлеттер бізбен қарастырылған шекті жағдайлар (синусоида мен импульсті функция) арасындағы аралық орынға ие болады және (2. 1) түріндегі сигнал көрінісінің қолданылуына негізделген, қалыптасқан келесі шарттарды қанағаттандыратын кейбір функциялар жиынын құрайды.
Вейвлеттің базисті функциялары
Вейвлеттердің базисті функциялары ретінде әртүрлі функциялар, оған қоса жақын немесе алыстатылған импульстармен өзгертілген синусоидалар, деңгейлерінің секірмелері бар функциялар және т. б. бола алады. Бұл жергілікті сигналдары мен үзілістері бар сигналдардың жеңіл көріністерін, сол немесе басқа түрдің вейвлеттер жиындарын қамтамасыз етеді және шығарылатын есептердің шарттарынан бастама алатын тура келетін вейвлеттердің таңдап алуларында жазықты ашады және бұндай шешімді мүлдем мылжыңсыз жасайды. Өкінішке орай, шамамен барлық вейвлеттерде бір өрнек түріндегі ұқсас көрініске ие болмайды, бірақ компьютерлермен оңай есептелінетін, итерациялы өрнектермен беріле алады.
Вейвлеттер өздерінің уақыттық және жиіліктік бейнелерімен сипатталады. Уақыттық бейне кейбір функциямен анықталады. Ал жиіліктік бейне оның
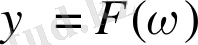 Фурье-түрімен анықталады, ол вейвлет спектрінің орнатып өтуін береді. Фурье-түр келесі өрнекпен анықталады
Фурье-түрімен анықталады, ол вейвлет спектрінің орнатып өтуін береді. Фурье-түр келесі өрнекпен анықталады
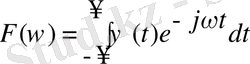 . (2. 2)
. (2. 2)
Осы вейвлеттердің кейбіреулері импульстермен өзгертілген кейбір “орташа жиіліктері” және аудандары (уақыт өсінің үстінде және оның астында) нөлге жақын синусоидалы тербелістерді еске салатыны, жақсы көрінген. Шын мәнісінде уақыттың өсінің үстінде және астындағы ауданның дәл нөлдік мәні (яғни интегралдың нөлдік мәні) - уақыттық тәуелділікті вейвлеттерге жатқызуға мүмкіндік беретін аса маңызды шарттардың бірі.
Вейвлеттерге салынған (таңылған) интеграл мәнінің нөлдік шарты
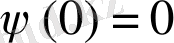 дегенді білдіреді, яғни Фурье-түрлендіруі жиіліктер өсі бойынша жылжытылған және кейбір нөлдік емес
дегенді білдіреді, яғни Фурье-түрлендіруі жиіліктер өсі бойынша жылжытылған және кейбір нөлдік емес
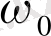 жиіліктің маңында орналасады, оны вейвлеттің орташа дөңгелектік жиілігі ретінде қарастыруға болады. 1-суреттен вейвлеттер шектелген жиіліктік спектрге ие екені және көптеген вейвлеттерде ол шыңы
жиіліктің маңында орналасады, оны вейвлеттің орташа дөңгелектік жиілігі ретінде қарастыруға болады. 1-суреттен вейвлеттер шектелген жиіліктік спектрге ие екені және көптеген вейвлеттерде ол шыңы
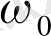 жиілікте орналасқан шолпуды еске салатыны көрсетілген. Егер вейвлеттерді өзгертілген синусоидалар ретінде жуықтап түсіндірсек, онда оның жиілігі вейвлеттің орташа жиілігі болады (2-суретті қараңыз) . Жалпы жағдайда, вейвлеттердің уақыттан тәуелділігі синусоидалыдан алыс болғанда, орташа жиілікті анықтау өңдеуді талап етеді және итерациялық әдіспен іске асады.
жиілікте орналасқан шолпуды еске салатыны көрсетілген. Егер вейвлеттерді өзгертілген синусоидалар ретінде жуықтап түсіндірсек, онда оның жиілігі вейвлеттің орташа жиілігі болады (2-суретті қараңыз) . Жалпы жағдайда, вейвлеттердің уақыттан тәуелділігі синусоидалыдан алыс болғанда, орташа жиілікті анықтау өңдеуді талап етеді және итерациялық әдіспен іске асады.
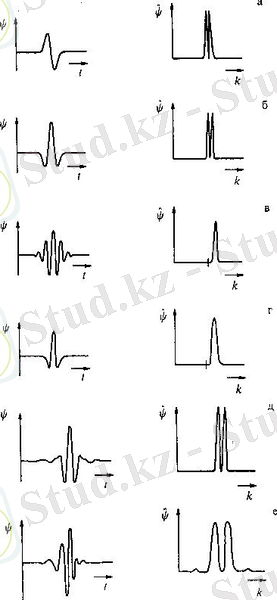
1-сурет-Жиі қолданылатын вейвлет мысалдары: (а) WAVE, (б) MHAT, (в) Morlet, (г) Paul, (д) LMB, (е) Daubechies. Вейвлеттердің уаытқа тәуелділігі (сол қатар) және олардың Фурье түрлері көрсетілген (оң қатар) .
Әртүрлі жиіліктері бар сигналдың құраушыларын сипаттау үшін вейвлетті созу немесе тарылту мүмкіншілігіне ие болу керек, ол үшін оның орташа жиілігін ауыстыру қажет. Егер вейвлет кеңістікте (уақытта) тарылса, оның “орташа жиілігі” өседі, вейвлеттің спектрі аса жоғары жиіліктер облысына ығысады және анықталмағандық принципіне сәйкес кеңейеді. Бұл құбылысты сызықты деп есептеуге болады: егер вейвлет екі есе тарылса, онда оның орташа жиілігі және спектрінің ені дәл осылай екі есе өседі.
Мұнда бір мезгілде уақытты және жиілікті облыстарда вейвлеттердің шоғырлануы мүмкін емес екендігін айта кету керек. Дегенмен, бұл жағдайды вейвлеттердің кемшіліктері деп бағалау дұрыс емес. Керісінше, Фурьенің терезелі түрлендірулерімен салыстырғанда, вейвлеттердің ерекше жақсы уақыттық шоғырлануы сигналдардың қысқа уақытты жергілікті ерекшеліктерінің көріністері үшін қажет вейвлеттердің сол спектрлі құрамаларының жиілігін өсіру үшін қажетті әдісті береді. Жалпы айтқанда, басында құбылыс микроскоп астында қарастырылады, ал кейін - лупа арқылы, кейін - құралсыз көзбен, ары қарай - бірнеше қадам қашықтықтан қарастырылады.
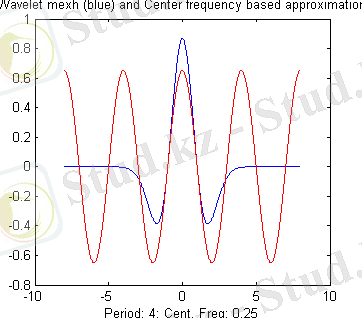
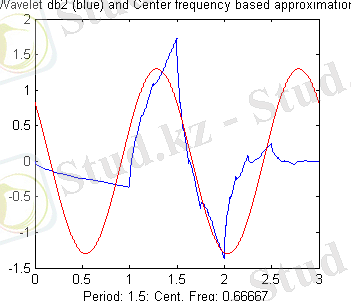
2-сурет.
Дегенмен, ортогоналдық қасиеттері жоқ бірқатар вейвлеттер бар, бірақ, оған қарамастан, іс жүзінде пайдалы, мысалы, талдау есептерінде сигналдар мен функциялардың жергілікті ерекшеліктерін ұқсастыруда.
2. 2. Вейвлет-түрлендірудің үздіксіз түзуі
Анықталғандық үшін,
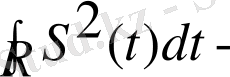 ға тең,
ға тең,
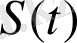 сигналдың энергиясы
сигналдың энергиясы
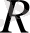 мәнді облыспен кеңістіктегі сигнал ақырғы болсын.
мәнді облыспен кеңістіктегі сигнал ақырғы болсын.
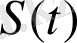 сигналдың үздіксіз түзу вейвлет түрлендіру (ПНВП) Фурье түрлендіруімен ұқсас түрі бойынша келесі өрнек бойынша вейвлет-коэффициенттерді есептеу жолымен берілсін:
сигналдың үздіксіз түзу вейвлет түрлендіру (ПНВП) Фурье түрлендіруімен ұқсас түрі бойынша келесі өрнек бойынша вейвлет-коэффициенттерді есептеу жолымен берілсін:
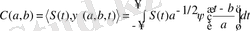 , (2. 3)
, (2. 3)
мұндағы
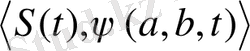 белгілеуі сәйкес көбейткіштердің скалярлы көбейтіндісін білдіреді. Сигналдарды анықтайтын облыстың шектелгендігін ескергенде және
белгілеуі сәйкес көбейткіштердің скалярлы көбейтіндісін білдіреді. Сигналдарды анықтайтын облыстың шектелгендігін ескергенде және
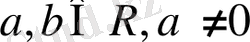 :
:
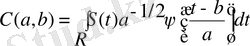 . (2. 4)
. (2. 4)
Сонымен, вейвлет-коэффициенттер вейвлет-функцияның берілген түріне сигналдың скалярлы көбейтіндісінің интегралдық мәнімен анықталады. (2. 4) өрнек Wavelet Toolbox пакетінде түзу үздіксіз вейвлет-түрлендірулер функциялары үшін негізгі болып қолданылады.
Түзу вейвлет-түрлендіруді
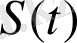 сигналдың немес кейбір дербес функциялардың мүмкін болатын барлық қозғалтулар мен созу/сығу бойынша сигналдың бөлінуі сияқты қарастыруға болады. Бұл кезде
сигналдың немес кейбір дербес функциялардың мүмкін болатын барлық қозғалтулар мен созу/сығу бойынша сигналдың бөлінуі сияқты қарастыруға болады. Бұл кезде
 және
және
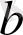 параметрлері оларды анықтайтын, жоғарыда көрсетілген облыстар шегінде кез-келген мәндерді қабылдай алады. Түзу Фурье түрлендірулерін қозғаулар бойынша бөліну (олардың графиктерінің орнын беретін, гармониктердің фазалық жылжу айтылады) және сығылулар/сығулар (гармониктердің амплитудаларының мәндерімен анықталады) сияқты қарастыруға болады, бірақ сигналдардың жергілікті ерекшеліктерінің көріністері үшін өте ыңғайлы емес, бір функцияға (синусоидаға) қолданылады.
параметрлері оларды анықтайтын, жоғарыда көрсетілген облыстар шегінде кез-келген мәндерді қабылдай алады. Түзу Фурье түрлендірулерін қозғаулар бойынша бөліну (олардың графиктерінің орнын беретін, гармониктердің фазалық жылжу айтылады) және сығылулар/сығулар (гармониктердің амплитудаларының мәндерімен анықталады) сияқты қарастыруға болады, бірақ сигналдардың жергілікті ерекшеліктерінің көріністері үшін өте ыңғайлы емес, бір функцияға (синусоидаға) қолданылады.
Жинақы тасымалдаушылары бар вейвлеттер үшін тәжірибеде шексіз шектері бар интегралдарды есептеу қажеті жоқ.
 және
және
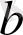 параметрлердің өзгеру облыстары шектелгендігін ескеруге болады. Мысалға, сол нәтижені
параметрлердің өзгеру облыстары шектелгендігін ескеруге болады. Мысалға, сол нәтижені
 нан
нан
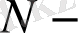 ға дейінгі шектерде интегралдау арқылы алуға болады. Бұл (2. 4) өрнек бойынша вейвлет-коэффициенттерді өрнектеуге сәйкес келеді.
ға дейінгі шектерде интегралдау арқылы алуға болады. Бұл (2. 4) өрнек бойынша вейвлет-коэффициенттерді өрнектеуге сәйкес келеді.
Вейвлет-түрлендіру берілген масштабта және талданатын сигналдың талданатын вейвлеттерінің скалярлы көбейтіндісі болғандықтан,
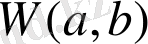 коэффициенттер құрамында талданатын вейвлет пен талданатын сигнал туралы (Фурье түрлендіруінің коэффициенттері сияқты, олардың құрамында сигнал және синусоидалы толқын туралы хабар бар) құрастырылған хабар бар.
коэффициенттер құрамында талданатын вейвлет пен талданатын сигнал туралы (Фурье түрлендіруінің коэффициенттері сияқты, олардың құрамында сигнал және синусоидалы толқын туралы хабар бар) құрастырылған хабар бар.
Талданатын вейвлеттің таңдауы, әдетте, сигналдан қандай хабарды алу керек екендігімен анықталады. Әрбір вейвлетте уақыттық және жиіліктік кеңістіктегі сипаттамалы ерекшеліктері бар, сондықтан кейде әр түрлі вейвлеттерің көмегімен қолданатын сигналдың сол не басқа қасиеттерін толығырақ айқындауға және астын сызуға болады.
2. 1. 3. функциялардың мысалдары
Салыстырмалы жақында қолданылатындықтан және математикалық аппаратты белсенді өңдеу сатысында болғандықтан, вейвлет-түрлену жақсы және кең танымал емес, сондықтан, үлкен көрнекілік үшін Фурье талдауымен ұқсастықтар мен салыстырулар жүргізе отырып, вейвлет-талдаудың қажетті түсініктемелерін енгіземіз, зерттеушілердің кең тобы үшін олардың тартымдылығы дайсыз және уақытпен тексерілген.
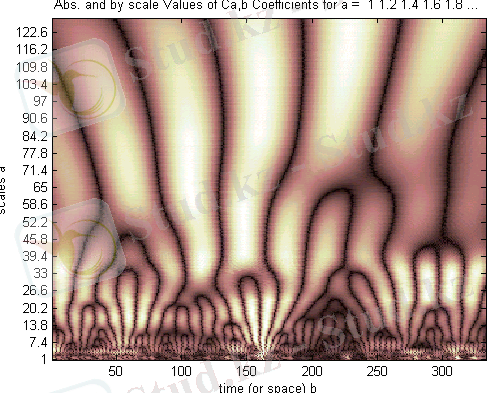
3-сурет - ҒС ағындарының уақыт бойынша өзгерісінің Вейвлет-спектрограммасы.
Анықтамалар, қасиеттер және олардың салдарлары берілген бір өлшемді функциялар, қатарлар үшін келтіріледі. Қажеттілік кезінде айтылғанның бәрі көпөлшемді тәуелді функциялар туралы, уақыттық қатарлар туралы және, сәйкесінше, жиіліктер туралы айтамыз. Дегенмен, жалпылықты бұзбаусыз тәуелсіз координата кеңістіктік (сәйкес толқындық сандармен) және кез-келген басқа бола алады.
Бір өлшемді сигналдың вейвлет-түрлендіруі масштабты өзгертулер мен тасымалдардың қатысуыен солитон тәрізді функциялардың (вейвлеттің) анықталған қасиеттеріне иелілігінен құрастырылған базис бойынша оның бөлінуінен тұрады. Осы базистің әрбір функциясы анықталған кеңістіктік (уақыттық - жиілікті сияқты, оның физикалық кеңістікте не уақытта) шоғырлануын сипаттайды.
Осылайша, сигналдарын талдау үшін қолданылатын салтты Фурье түрлендіруінің вейвлет-түрлендірудің ерекшелігі зерттелетін бір өлшемді сигналдың екі өлшемді ұңғылауды қамтамасыз етеді, бұл кезде жиілік пен координата тәуелсіз айнымалылар сияқты қарастырылады. Нәтижесінде сигналдың қасиеттерін бір уақытта физикалық (уақыт, координата) және жиіліктік кеңістіктерде талдауға мүмкіншілік пайда болады. Айтылған бір өлшемсіз сигналдар мен функцияларға жеңіл жалпыланады.
Шетелдік әдебиетте вейвлет-түрлендірулер коэффициенттері негізінде алынған time-scale немесе wavelet spectrum спектрге қарағанда Фурье спектрін single spectrum деп атау қабылданған.
Көптеген тәжірибелердің нәтижелері Рейнольдс санының үлкен мәндері кезінде турбулентті сұйықтау көлемінің бөлігі энергияның диссипациясына қатысты пассивті болып қалуын айғақтайды. Вейвлет-талдау кезектесумен жүретін құбылыстарды талдау үшін өте ыңғайлы болады. Ол меңгерілетін заттың кеңістікте таралған қасиеттерін шығаруға, зат туралы жергілікті жоғары жиіліктік және ғаламды үлкен масштабты хабар алуға және көптеген басқа жеткілікті дәл және артықшылықтары жоқ болуға мүмкіншілік береді. Көптеген зерттеушілердің вейвлет-талдауды “математикалық микроскоп” деп атауы кездейсоқ емес - атау әртүрлі масштабтарды жақсы рұқсатта әдістің керемет қасиетін сақтауды тамаша шағылдырады. Бұл “микроскоптың” маңызды біртекті емес заттың ішкі құрылымын және көптеген, дербес жағдайда фракталды Вейерштрасс функциялары мен канторлы қатарлардың ықтималды өлшемдері сияқты классикалық мысалдарда көрсетілген оның жергілікті скейлингті қасиеттерін меңгеруді айқындау мүмкіншілігі болып табылады. Вейвлет-талдаудың Рейнольдс сандары үлкен кезде желдік туннельде турбулентті өрістің жылдамдығына қолданылуы алғашқыда Ричардсон каскадының бар болуының дәлелдеуін берді. Энергетикалық каскадты құбылыстардың мультифракталды біртекті емес канторлы қатарлардың құрылымымен ұқсастығы көрсетілген. Аса әсерлі болып вейвлет-талдауды диссипативті жүйелерде жағдайлардың хаосқа өту бақылауларын өзгертерін, кейбір жақсы танымал динамикалық жүйелердің мультифракталды инвариантты өлшемдерге қолдануы шықты.
Бірмәнді мөлшерлі айқындау мен бейстационарлы, шапшаң айнымалы сигналдардың (уақыттық қатарлардың) (уақытта және кеңістікте) ерекшеліктердің теңестірулері үшін фракталды, информациялы-энтропиялы талдаулар сияқты қазіргі заманғы әдістерді пайдалану қажет. Бұл әдістер толығырақ екінші бөлімде сипатталады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz