Фракталдар

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Фракталдар.

Табиғатта кездесетін өлшемдері атомдық масштабтан әлемдік кеңістікке дейін созылып жатқан обьектілердің (нысандардың) геометриясы біздің оны зерттеп түсіну үшін құратын, идеалдандырылған модельдерімізде басты орын алады. Бірақ дәстүр бойынша табиғат геометриясын индуктивті түсінудің негізі ретінде осы уақытқа дейін евклидтік геометрияның түсініктері: сызықтар, шеңберлер, сфералар мен тетраэдрлар қолданылады.

Күрделі жүйелерде болатын процестерді, құрылымды - стохастикалық құбылыстарды барынша қарапайым түрде сипаттауға, түсіну мен түсіндіруге мүмкіндік беретін ғылым - фракталдар теориясы.

Фрактал түсінігі алғаш математикалық түрде күрделі геометриялық формаларды сипаттау үшін енгізіледі. Ғылымның дамуы және компьютерлік техниканы қолданудың алуан түрлі мүмкіндіктері фрактал түсінігінің табиғаттың ең жалпы, түбегейлі заңдылықтарымен байланысты екенін көрсетті. Физика - математика ғылымдарының бұл жаңа бағытының күрт дамуына француз ғалымы Б. Мандельброттың 1982 жылы жарық көрген "Табиғаттың фракталдық геометриясы" атты кітабының шығуы тікелей себеп болды.

Б. Мандельброт бұл кітабында табиғатта кездесетін фракталдық нысандардың көптеген мысалдарын келтірді және оған ғылыми көпшіліктің жаппай назарын аударды. Оның дамытқан геометриясы сан түрлі обьектілердің формасын сипаттауға қолданылуымен қатар, заңдылығы бар, масштабты - инварианты құрылымдарның моделін салуға мүмкіндік береді. Осы үлгілерді қолдану ретсіз құрылымдарды зерттеп білудің жаңа жолдары болып табылды.

Аспандағы бұлттар, тау сілемдері, терезе шынысына қатқан қыраулар, полимерді түзетін молекулар, тірі клеткалар және тағы сол сияқты нысандар мен құрылымдардың бәріне ортақ бір қасиеті - олардың кіші және бөліктерінің бір - біріне ұқсастығы. Әртүрлі уақыт мезетінде түсірілген, үлкен және кіші бұлттардың суреттерін салыстыру олардың өзгеру заңдылығының бірдей болатынын көрсетеді. Осы сияқты заңдылықты әртүрлі масштабта түсірілген жағалау сызықтарының фрагменттерінін (мысалы, Британия аралының, Арал теңізінің, Балқаш көлінің) салыстыру арқылы да байқауға болады.

Осындай өзұқсас нысандар үшін француз математигі Б. Мандельброт жаңа фрактал (латыншадан аудармасы - бөлшектік, кескіленген) ұғымын енгізді. Ол құрылымдық, өзіне - өзі ұқсас иерархиялық ішкі құрылысы бар обьектілерді фракталдар деп аталады. Фракталдық қасиет бейсызық процестер мен құбылыстарды сипаттайтын фазалық кеңістіктерде, күрделі жүйенің функционалды харакеттерінде, адрондардың әсерлесуінің, қоғамның экономикалық көрсеткішінің өзгерістерінде және т. б. байқалады.

Фракталдардың дәл және қатаң анықтамасы әзірге жоқ. Б. Мандельброт алғаш рет фрактал анықтамасының мынадай вариантын ұсынған: фрактал деп тұтас күйіне белгілі бір мағынада ұқсас бөліктерден тұратын құрылым айтылады.

Математикада өзұқсас геометриялық обьектілер деп бір-бірі ұқсас, саны шекті бірдей элементтерге бөлуге болатын денелер саналады. Мысалы, төменде кесіндіні, тең қабырғалы үшбұрышты, квадратты, кубты сәйкес 2, 4, 4, 8, өзұқсас элементтерге бөлу тәсілі келтірілген. Суреттен фракталдың қандай масштабта байқалғанына қарамастан бір-біріне ұқсас, бірдей түрге ие екендігі білінеді. Бірақ, қосымша еш информация алмай, біртіндеп кішірейіп немесе үлкейіп отыратын өзұқсас өркеш - өркеш бұлттардың сыртқы пішінінің өлшемдерін бағалау мүмкін емес. Себебі, бұл кезде элементтер саны өте көп және олар бірсыдырғы орналаспайды. Бұл үшін арнайы өлшемділік ұғымы енгізілуі тиіс.

Жалпы өлшемділік ұғымы кеңістіктегі нүктенің орнын анықтауға мүмкіндік беретін, ең аз тәуелсіз координаталар санын анықтаумен тығыз байланысты. Физикада бұл геометриялық обьектіні бейнелеуге мүмкіндік беретін тәуелсіз айнымалылар санымен - параметрлік өлшемділікпен сәйкес келеді. Евклид кеңістігіндегі көлемді анықтауға керекті бұндай айнымалыларды саны үшке тең (x, y, z), жазықтықтың ауданын өлшеуге оның екеуі (x, y) болса, ал сызық үшін бір координата x болса да жеткілікті. Нүктенің өлшемділігі нөлге тең. Осы жағынан кеңістік үш өлшемді, жазықтық екі өлшемді, ал сызық бір өлшемді деп айтылады, яғни, параметрлік өлшемділіктің мәндері бүтін сандар 0, 1, 2, 3.

Өлшемділіктің екінші түріне топологиялық өлшемділік d жатады. Топологиялық өлшемділіктің анықтамасы былай беріледі: кез - келген жиынның топологиялық өлшемділігі оны екі, өзара байланыссыз бөліктерге ажырататын қиманың өлшемділігіне бірді қосқанға тең. Түзуді екі байланыссыз кескіндерге бөлу оның бір нүктесін алып тастау арқылы жүзеге асырылады. Ал шекті нүктелер жиынының өлшемділігі нөлге тең болғандықтан, сызық бір өлшемді, яғни 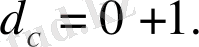Жазықтық екі өлшемді, себебі, оны екіге бөлуді өлшемді, екіге тең, яғни, 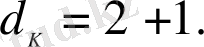Демек, топологиялық өлшемділіктер де 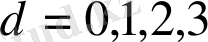бүтін сандар.

Бірақ, табиғатта кездесетін кейбір нысандарды өлшеу үшін, бұл өлшемділіктер жеткіліксіз болып шықты. Себебі, адамның сезім мүшелерінің қабылдау шегін әртүрлі сезімтал құралдар (микраскоптар, телескоптар және т. б. ) арқылы басқа деңгейге ауыстыруға болады, бірақ барлық масштабты бір мезгілде қадағалау және нысандардың өлшемдерінің әртүрлі масштабта қандай қатынастарда болатынын тағайындау қиын. Информациялық қордың молаюы мен ғылыми - техникалық прогресс бұл қиындықты жеңуге мүмкіндік берді.

Алғаш рет күрделі нысандарды өлшеуді ағылшын физигі Л. Ричардсон жүзеге асырды. Ол фракталдық құрылымдардың бәріне ортақ маңызды ерекшеліктерінің бірі - олардың аддитивті еместігін, яғни, өлшенетін шама (ұзындық, аудан, көлем, масса, заряд, және т. б. ) мәндерінің кеңістікте жүргізілген өлшеулердің дәлдігіне тәуелділігін пайдаланды. Мысалы, аса күрделі, шым - шытырық броундық бөлшектің траекториясының ұзындығы L , өлшеу бірлігіне 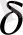(масштабына) байланысты. Масштаб кішірейген сайын өлшенген обьектінің ұзындығы арта береді.

Л. Ричардсон Британия аралының әртүрлі масштабта түсірілген карталарын алып, оның А және С нүктелерінің арасын қосатын жағалау сызығының ұзындығын анықтау үшін адымы 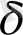- ға тең ашамен өлшеулер жүргізіледі. (1 - сурет ) . А нүктесінен С нүктесіне дейін жүріп өткендегі аша адымының 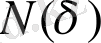санын білу арқылы Л. Ричардсон өлшенетін жағалау сызығының ұзындығын мына өрнекпен анықталады.

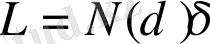(1. 1)

Бұл кезде 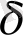масштабтың ішіне кіретін кіші иілулер, ойыстар мен дөңестер есептелмейтіні белгілі. Л. Ричардсон өлшеу масштабын кеішірейтіп, өлшеулерді қайталады. Енді бұрынғы көптеген иілулер, дөңестер есептелгендіктен, өлшенген ұзындық біршама өсті. Сөйтіп ол ашаның адымын үнемі кішірейтіп отыру жағалау сызығының ұзаруына әкелетін шексіз өзгертулер енгізуге мүмкіндік беретінін байқады. Сонымен, айыру қабілеттілігін арттыру, яғни, өлшеу масштабын кеміту әр кезде күрделі сызықтардың ұзаруына әкеледі.

1. 9 сурет - Теңіз жағалауының фрагменті.

Фракталдық нысандарды өлшеудің тағы бір тәсіл - өлшенетін нысандарды өлшеуді немесе оның фрагментін, қабырғаларының ұзындығы 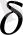- ға тең, квадрат ұяшықтардан құралған торлармен жабу. Бұл кезде де өлшенетін фракталдық нысанды түгел жабатын ұяшықтар саны 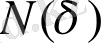анықталады (1. 9 - сурет) .

Тәжірибелер, жағалау сызығының фрагментін жабатын, квадрат ұяшықтарының саны, жуық шамамен сол қашықтықты түгел өтетін аша адымының санына тең болатынын көрсетті. Егер жағалау сызығы тұрақты 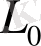ұзындыққа ие болса, онда оны жабатын квадрат ұяшықтарының саны өлшеу масштабына кері пропорционал, ал (1. 1) өрнекпен есептелетін жағалау сызығының ұзындығы, 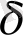кішірейген сайын, тұрақты 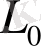- ге ұмтылар еді. Әрине, бұл әдіспен өлшеу кезінде де 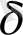кішірейгенге артатындығы байқалады.

Сонымен, Л. Ричардсон өлшеу масштабы кеміген сайын, фракталдық обьектінің жағалау сызығының өлшемі дәрежелік заңмен өсетінін тағайындады.

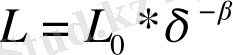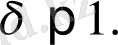, (1. 2)

Мұндағы 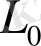- өлшенетін обьектінің бастапқы және соңғы нүктелерін қосатын түзудің ұзындығы, 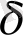- өлшемсіз шама.

Бұл өрнек Ричардсон заңы деп аталады. Дәрежелік көрсеткіш 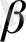оң мәнге ие болуы тиіс. Жағалау сызығының ұзындығын тормен өлшеу тәсілінде де, 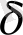өлшеу масштабының кемуі торды түзетін квадрат ұяшықтардың санын көбейтетін болғандықтан Ричардсон заңы орындалады.

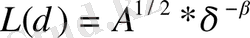, (1. 3)

бұл жерде А - қабырғаларының ұзындығы 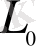квадраттың ауданы. Өте кіші масштабтарда " жағалау сызығы " ұғымының мәні жоғалады. Ал атом аралық қашықтықтарда " аша адымы ", " квадрат ұяшық " ұғымдары да өз мәндерін жоятыны түсінікті. Себебі, бұл кезде кванттық механиканың зерттеу обылыстарына енеміз. Бірақ, қалай дегенмен, Ричардсон заңы кең масштабты диапазонда орындалатыны дәлелденді. Осыдан жоғарыда тағайындалған физикалық заңдылықтың сипатын түсіну мен түсіндірудің математикалық құралы болуы тиістігі туындайды.

Бұл құралды табу үшін кез - келген физикалық шаманы өлшеу процесінің жалпы сатылары қарастырылады, себебі, (1. 2), (1. 3) жаңа дәрежелік заңдар өлшеу нәтижелеріне сүйеніп тағайындалған. Біз, обьектінің санақ жүйелерінің өзгерстеріне байланыссыз тұрақты сипаттамаларын, яғни, инвариантты сипаттамаларын қарастырамыз. Обектінің инвариантты сипаттамаларының аддитивті (обьектінің сипаттамасы оны қосындысына тең) және скалярлы болатыны белгілі.

Жиындар теориясында инвариантты, аддитивті және скалярлы қасиеттерге ие сипаттамалар өлшем деп аталады. Класикалық физикада обьектінің өлшемі ретінде ұзындық аудан, көлем, заряд, масса, олардың байқалу ықтималдығы және т. б. жатады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.