Автотербелмелі жүйе - Ван-дер-Поль генераторы

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Жүйенің фазалық кеңістігінде оқшауланған тұйық траекториямен бейнеленетін бастапқы шартқа тәуелсіз біраз уақыттан кейін кейбір арадағы траекториялар тартылатын периодты асимптотты орнықты қозғалыстың болу мүмкіншілігі тек бейсызықты диссипативті жүйелерде ғана қамтамасыз етіледі. Бұл динамикалық жүйе түрінің тербелмелі процестерін зерттегенге қажет болғаны соншалық А. А. Андронов оған арнайы термин - автотербелмелі жүйе деген ұғым енгізді [9] .

Динамикалық жүйедегі автотербеліс периодты ғана емес, сондай-ақ квазипериодты және онымен қоса стохасты та болуы мүмкін [4] . Сондықтан біз тек жеткілікті жалпы анықтамасын береміз. Автотербеліс - бұлар өшпейтін тербелістер, түрі және қасиеті осы жүйенің өзімен сипатталатын бейсызықты диссипативті жүйедегі сыртқы энергия көзімен қуаттандырылады және бастапқы шартқа тәуелді емес (соңғы шектелуімен) . Автотербелістер диссипативті жүйелердегі басқа тербелістерден негізінде мүлдем ерекшеленеді, оларды үзбеу үшін сырттан периодты әсер қажет емес.

Математикалық түрде автотербелмелі жүйеде периодты қозғалысқа - Пуантренің шекті циклі жауап береді [9] . Бұл терминдер тербеліс теориясында орнықты бекітілген.

Динамикалық жүйенің мысалы ретінде Пуанкаренің шекті циклімен классикалық бейсызық Ван-дер-Поль осцилляторын қарастырамыз. 4-суретте Ван-дер-Поль генераторының принципиалды сүлбесі келтірілген.

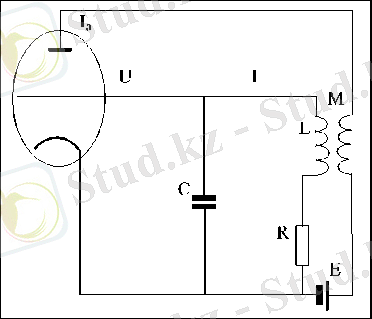
$C:\Users\User\Downloads\media\image4.png$

сурет. Тор тізбегіндегі тербелмелі контурлыВан-дер-Поль генераторының принципиалды схемасы

Алдымен, осы генератордағы автотербелістің туу жағдайын сапалы сипат- таймыз. ЬС контурда пайда болған кішкене тербелістер торлы кернеулі V пери- одты басқарады. Пайда болған анодты ток І _а өздік индукциямен М қамтамасыз етілген оң кері байланыс арқылы осы тербелістерді күшейтеді.

Тербелістің амплитудасының өсуімен қанығуы болады және контурға енгізгенімен энергия сол контурдағы энергияның жойылуымен салыстырғанда одан ары амплитуданың өсуі тоқтатылады.

Енді жүйенің сандық талдауына келеміз. Біз ЭҚҚ-нің Е ішкі кедергісі мен торлы токты ескермей, 4-суреттегі схема үшін уақыты і арқылы анықтап, Кирх- гоф заңын жазамыз.

/ = -С </и/ с/1 , (12)

Ш = ІІ-Ь(ЩА-М(П _а І& (13)

Тіктіктің анодты-торлы сипаттамасын 8(Ц) = <Я _а /<Ю анықтай отырып, жүйені бейнелейтін теңдеуді аламыз:

ЬС^-= [і8(ІІ) -КС~^-ІІ. (14)

аи ш

$C:\Users\User\Downloads\media\image5.png$ Триодтың анодты-торлы сипаттамасының түрі 5-суретте көрсетілген. Анод- ты ток торлы кернеудің бойымен өседі. Бірақ бұл өсу шексіз емес, қанығу кернеуі Цд деп аталатын торлы кернеуге жеткізетін анодты токтың кейбір мак- симальды шамасымен шектелген. Торлы кернеудің одан кейінгі өсу кезінде анодтағы ток өспейді.

сурет. Триодтың сипаттамасы: анодты токтың торлық кернеуден тэуелділігі (-) жэне оның туындысы ( ) . (Л, - канығу кернеуі

Соған сэйкес түрі Х(і/) = </і _и /</і/ сондай-ақ 5-суретте көрсетілген. Енді өлшемсіз шамаларды енгіземіз:

и = -

х = (ЬС) ~ ¹² ,

(15)

/ (и) =

КС

(ЬС)

М8 (Ц)
(КС)

-1

және өлшемсіз уақыт х бойынша туындысын штрихпен анықтайтын боламыз. Біздің жүйемізді бейнелейтін теңдеудің өлшемсіз түрі, екі теңдеудің 1-ретті жүйе түрінде былай жазылады:

и'= у, V = /(и) у-и . (16)

Әрине /(и) функциясы осыған ұқсас түрге ие болу керек, мысалы 5-суреттегі

қисық. /(//) = 0 кезінде, мысалы контурдағы жойылу жоқ кезінде бүл жүйе

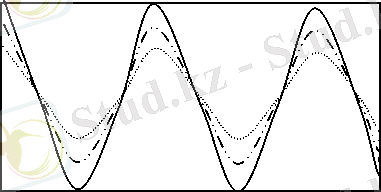$C:\Users\User\Downloads\media\image6.png$ $C:\Users\User\Downloads\media\image7.png$ еркін амплитуданың кәдімгі (қарапайым) гармониялық тербелісін бейнелейді (6-сурет) .

сурет. _/(и) =0 кезіндегі фазалық портрет(солжагындағы) және тербеліс түрі (оң жагындағы) . Екі суреттегі қисықтардың бір түрлі болуы дәл солбір жағдайды бейнелейді

Біз Ван-дер-Поль теңдеуін сандық модельдеуіне ыңғайлы мына түрін қарастырамыз:

х - д(1 - Ъх ² ) х + х = 0 .

(17)

4-5-ДӘРІС

Периодты сигналдар

Анықтама бойынша периодты функция деп мына шартқа жауап беретін функцияны айтады:

і<}і( + й^й = 1, 2, . . . , (1)

мұнда Т - функцияның периоды.

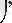
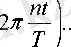
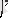$C:\Users\User\Downloads\media\image8.png$ $C:\Users\User\Downloads\media\image9.png$ $C:\Users\User\Downloads\media\image11.png$ $C:\Users\User\Downloads\media\image12.png$ $C:\Users\User\Downloads\media\image13.png$ $(і) функцияның спектрлік жіктеуін анықтау үшін келесі функциялардың жиынтығын қарастырайық:

, Л - 81П

уІ Т \Т

² 4}# ^ш г?

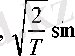
$C:\Users\User\Downloads\media\image10.png$

- С08

- соз[ 2ж - \ . 1- соз[ 2я -

т \ т \т \ т

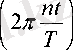
$C:\Users\User\Downloads\media\image14.png$

(2)

Қысқаша и _ш < деп белгіленген, (2) -жиынтықтағы кез-келген функция (1) - периодтылық шартын қанағаттандырады.

Келесі үш интегралды қарастырайық:

со. у( 2ж ^ХсоІ 2л^ү\ с!( = <

0, т^п, \, т = п = 0, 2, т = п = 0;

(3)

ү со8^2л--^^8Іп^2л-2^і/ ¹ = 0;

тЛ

пі

С05 2 п 57И 2 п - щі = <

Г Т

0, т <£ п, \, т = п = 0, 2, т = п = 0.

(3) -ші шартты қанағаттандыратын функцияларды ортогональды, ал еселі жиілікті гармониялық функциялармен пайда болған (2) -ші функциялар жүйесін, ортонормаланзан базис деп атайды. Ортогональдылық шартын Кронекер символы арқылы қысқаша түрде жазуға болады: