Кездейсоқ сигналдар мен процестердің статистикалық сипаттамалары, стационарлық және эргодиялық қасиеттері


КЕЗДЕЙСОҚ СИГАЛДАР
Кездейсоқ сигналдардың (КС) мәндерiн алдынөала дәл анықтауға мүмкiн емес, оларды тек кейбiр ықтималдықпен болжауға болады. Мұндай сигналдардың сипаттамалары статистикалық болып табылады.
Уақытта өзгеретiн КС-ң математикалық моделi кездейсоқ процесс (КП) д. а. Анықтама бойынша, Х{t} КП - түрi ерекше функция, оның кез-келген t уақыт мезетінде алатын мәндерi кездейсоқ шамалар б. т. Техникалық әдебиетте КС мен КП терминдерi жиi бiрдей мағынада қолданылады.
Тiркелуіне (қабылдауына) дейiн КС-ды кездейсоқ процесс ретiнде, яғни белгiлi бiр ортақ статистикалық заңдылыққа бағынатын x k (t) уақыт функцияларының жиынтығы (ансамблi) ретiнде қарастыру керек. Сигнал қабылданғаннан соң толығымен белгiлi болған бұл функциялардың бiреуi КП-ң жүзеге асырылуы (реализациясы) д. а. Уақыттың кездейсоқ емес, детерминдi функциясы болып табылатын бұл жүзеге асырылу болуы мүмкiн функциялардың шексiз жиынының бiреуi б. т. Осы суретте бiр КП-ң бiрнеше жүзеге асырылуларының мысалы келтiрiлген.
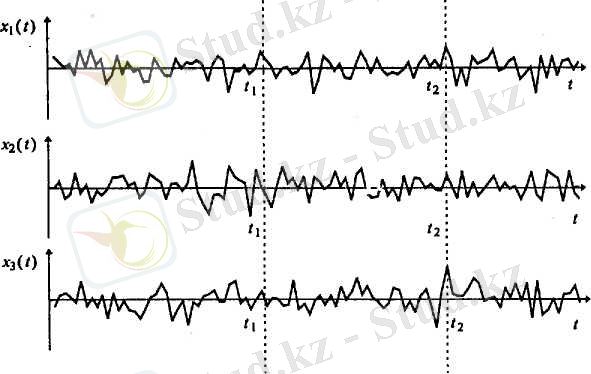
1 сурет - КП-ң жүзеге асырылулары
КП-ң қасиеттерiн анықтайтын ықтималдық сипаттамалары ансамбль үшiн, яғни уақыттың шексiз интервалында тiркелетiн жүзеге асырылулардың шексiз жиыны үшiн, енгiзiледi. Демек, КП-тiң сандық сипаттамаларын тек өте көп балама тәжiрибелердiң нәтижелерi болған жағдайда табуға болады.
Бiрақ, зерттеушi қолында әдетте КП-ң ұзындығы шектi жалғыз жүзеге асырылу болады, оны таңдама функциясы деп, не жай таңдама деп атайды. Егер таңдама мәндерi уақыттың дискрет мезеттерiнде алынатын болса, онда бұл таңдама уақыттық қатар б. т. Таңдама бойынша, не таңдамалардың шектi жиыны бойынша есептелетiн КП-ң сипаттамалары таңдамалық д. а. да, КП шын сипаттамалырының бағалауы ғана б. т.
КП iшiнде мәндерi үздiксiз, дискреттi және аралас процестердi бөлуге болады.

2 Сурет - Үздiксiз (а), дискреттi (б) және аралас (в) кездейсоқ процестер жүзеге асыруларының мысалдары
Х{t i } кездейсоқ шамалары белгілі бір мүмкінді мәндер аймағының шегіндегі кезкелген мәнді қабылдай алатын процесс мәндерi үздiксiз КП д. а. Мұндай процестің мысалы - жел жыллдамдығының уақыттағы өзгеруі, температураның өзгеруі, өткізгіштердегі жылулық шуыл, т. с. с.
Егер КП тек кейбір белгілі (анықталған) мәндерді қабылдай алса (рұқсат етілген мәндердің саны шексіз де болуы мүмкін), ал басқа ешбір мәндерге ие бола алмаса, бұл КП дискретті д. а.
Аралас КП -ң мәндерi үздiксiз және дискретті құраушылардың екеуі де бар.
Жүзеге асырудың түрi парметрлердiң (кездейсоқ шамалардың) шектi санымен анықталатын КП квазидетерминдi КП д. а. Мұндай процесс жағдайында жүзеге асырудың келешек мәндерiн алдында тiркелген мәндер негiзiнде алдын-ала дәл анықтауға болады. Мұндай процестiң мысалы - реализациялары амплитудасы мен жиiлiгi белгiлi (детерминдi), ал бастапқы фазасы кездейсоқ, [0, 2π] интервалында бірқалыпты үлестірілген, гармониялық тербелiстер б. т. процесс.
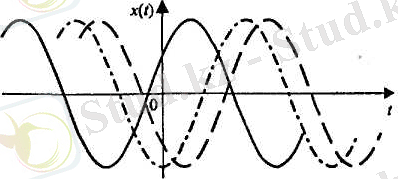
3 сурет - Бастапқы фазасы кездейсоқ гармониялық сигналдың жүзеге асырылулары
Егер келешек мәндердi алдын ала анықтауға мүмукiн емес болса, процесс детерминдi емес д. а.
Ықтималдық сипаттамалары уақытқа тәуелсiз болған процестер стационар д. а.
Кейбiр стационар процестер үшiн мынадай қасиет тән: ансамблiнiң әр мүшесi статистикалық мағынада өзiн барлық ансамбль сияқты жүргiзедi. Бұл жағдайда КП барлық сипаттамаларын жалғыз жүзеге асырылу қасиеттерiн зерттеп талдауға болады. Былайша айтсақ, оның қайсы -бiр статистикалық сипаттмаларын анықтағанда жиын (ансамбль) бойынша орташалауды жалғыз, теорияда ұзақтығы шексiз, жүзеге асырылуды уақыт бойынша орташалауға ауыстыруға болады. Мұндай процестердi эргодиялық ( қатаң мағынада эргодиялық ) д. а. Қатаң мағынадағы эргодиялық процестер қашанда-да стационар болып табылады. Барлық стационар емес процестер эргодиялық емес болады, бірақ стационар КП де эргодиялық емес болуы мүмкін.
Әдетте кейбiр физикалық процестің эргодиялылығын дәлелдеуге қиын болады, өйткенi iс жүзiнде бiл процестiн тек жалғыз жүзеге асырылуды өлшеуге мүмкiн болады. Бiрақ жиi физика тұрғысынан қарсы шығатын маңызды дәлелдер болмаса, процес эргодиялық б. табылады деп болжауға пайдалы болады. Процесс эргодиялық б. табылады деген болжау жағдайында уақыттық қатарларды талдау әлде-қайда оңайланады.
Кездейсоқ процестердің ықтималдықтық сипаттамалары
X(t) - {x 1 (t), x 2 (t), . . . , x k (t), . . . } жүзеге асырылулар ансамблімен берілген кездейсоқ процесс болсын. Уақыттың кайсыбір t 1 мезетін таңдап, барлық реализациялар (жүзеге асырылулар) алатын мәндерді анықтайық (бекітейік) : {x 1 (t 1 ), x 2 (t 1 ), . . . , x k (t 1 ), . . . } (1 суретті қара) . Бұл мәндердің жиынтығы кездейсоқ процестің бірөлшемді қимасын түзеді және X(t 1 ) кездейсоқ шама б. т. Берілген бір реализация t 1 уақыт мезетінде қабылдайтын x k (t 1 ) мәні X(t 1 ) кездейсоқ шаманың мәні б. т. КП-ң жүзеге асырылулары мен жүзеге асырылулар ансамблі X(t i ) кездейсоқ шамалардың жиыны б. т. Сондықтан кездейсоқ шамалардың ықтималдықтық түрдегі сипаттауы КП-ң сипаттауы болады, ал кездейсоқ шаманың статистикалық сипаттамалары КП-ң статистикалық сипаттамаларымен бірдей болады. Кездейсоқ шамалардың негізгі сипаттамаларын естеріңізге түсірейік.
Функциялық сипаттамалар
Кездейсоқ шамалардың мәндерін олар өлшеніп отырған тәжірибенің шарттары толығымен болса да алдын-ала анықтау мүмкін емес, тек бұл шама кейбір мәнге ие болуының ықтималдығын айтуға болады. Бірақ, кездейсоқ шамалардың ықтималдық үлестіруін біле отырып, КП реализацияларының қасиеттері мен олардың ерекшеліктері туралы қорытындыны жасауға болады.
F(x, t
1
) деп белгілінетін
ықтималдықтың үлестірілу функциясы
(ҮФ) (cumulative distribution function, CDF) КП-ң
t
1
мезетіндегі мәні
х
-тен көп болмайтынының ықтималдығына тең:
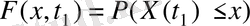
ЫҮФ азаймайтын функция, оның мәндері 0 ≤ F(х, t 1 ) ≤ 1 аралығында жатады. Шекті мәндер үшін мынадай қатынастар орындалады: F(-∞, t 1 ) = 0 и F(∞, t 1 ) = 1
КП мәнінің (а, b] интервалына түсу ықтималдығы ҮФ-ң бұл интервал шеттеріндегі мәндерінің айырмасына тең болады:
Р(а < X(t 1 ) ≤ b) = F(b, t 1 ) - F(a, t 1 ) .
Ықтималдықтың бірөлшемді тығыздығы (ЫТ) (probability density function, PDF) p(x, t 1 ) деп белгіленеді де, ҮФ-ң туындысы б. т. :
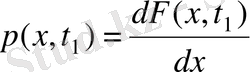 .
.
р(х t 1 ) dx көбейтіндісі КП-ң X(t 1 ) мәнінің х маңайындағы dx шексіз аз интервалына түсу ықтималдығын береді:
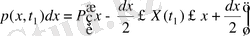
Демек ЫТ теріс емес функция б. т. : р(х, t 1 ) ≥0. X(t 1 ) мәнінің [а, b] интервалына түсу ықтималдығын анықтау үшін мынадай интегралды есептеу керек:
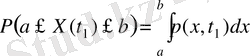
Мысалы, бірдей шуыл генераторлардың көп саны қосылған болсын.
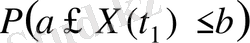 шама уақыттың
t
1
мезетінде
k
-інші генератордың
x
k
шығысы
a
мен
b
арлығында жататындығының ықтималдығын сипаттайды.
шама уақыттың
t
1
мезетінде
k
-інші генератордың
x
k
шығысы
a
мен
b
арлығында жататындығының ықтималдығын сипаттайды.
Кездейсоқ шама қайсыбір мәнді міндетті түрде алатындықтан, нормалаудың шарты орындалуы тиіс:
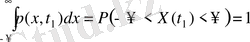 (4. 1)
(4. 1)
ЫТ біле отырып, ҮФ-ны да есептеуге болады:
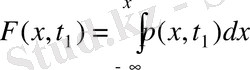 (4. 2)
(4. 2)
Сандық сипаттамалар
БЫТ білу Х( t 1 ) кездейсоқ шама мен оның кез келген функциясын статистикалық түрде орталауға мүмкіндік береді. Статистикалық орталау (ensemble averaging) деп процестің кейбір қимасындағы, яғни уақыттың бекітілген мезетіндегі, жиын бойынша (жүзеге асырылулар ансамблі бойынша) орталауды айтады.
ЫТ-ы р x (х) тең кейбір х кездейсоқ шаманың f функциясының математикалық үміті былай анықталады:
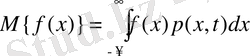 (4. 3)
(4. 3)
f(x) =x n түріндегі функция көмегімен кездейсоқ шаманың бастапқы моменттері:
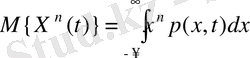 (4. 4)
(4. 4)
және центрлік моменттері енгізіледі:
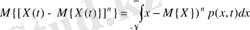 (4. 5)
(4. 5)
Кездейсоқ шаманың математикалық үміті (күтілімі) (mean value) (бірінші бастапқы момент, (4. 4) формуладағы n= 1, немесе (4. 3) формуладағы f(x) =x ) КП-ң t уақыт мезетіндегі орташа мәнінің теориялық бағалауы б. т. :
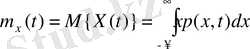 (4. 6)
(4. 6)
Дисперсия (variance) (екінші центрлік момент, (4. 5) формуладағы n=2 ) флуктуациялар деп аталатын КП-ң m x (t) орташа мәнінен ауытқулардың орташа қуатын сипаттайды:
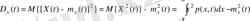 (4. 7)
(4. 7)
Орташа квадраттық ауытқу (standard deviation) дисперсияның квадраттық түбіріне тең және КП мәндерінің математикалық үмітке қатысты шашыраудың амплитудалық мөлшері б. т. :
 (4. 8)
(4. 8)
Х
кездейсоқ шаманың дисперсиясы жиі
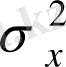 .
деп белгіленеді
.
.
деп белгіленеді
.
Эргодиялық процестер үшін жүзеге асырылулар ансамблі бойынша орталаудың орнына бір реализацияны бақылау уақыты бойынша орталау жүргізеді:
(4. 9)
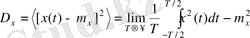 (4. 10)
(4. 10)
Бұрыштық жақшамен уақыт бойынша орташалау белгіленген. Стационар (оның ішінде эргодикалық та) процестердің математикалық үміті мен дисперсиясы уақытқа тәуелді болмағандықтан Уақыттың бекітілген мезеттерінің белгілері жіберілген.
Іс жүзінде интегралдау шексіз емес, шекті интервалда жүргізіледі, неғұрлым есептеудің дәлдігіне қойылатын талаптар жоғары болса, соғұрлым бұл интервалдың ұзындығы да көп болу тиіс.
Эргодиялық КП математикалық үміті оның кезкелген жүзеге асырылуының тұрақты құраушысына тең, ал дисперсия оның флуктуациялық құраушысының куатын сипаттайды.
Бірқалыпты үлестірім
БҮ (uniform distribution) - іс жүзінде жиі қолданатың кездейсоқ шамалар үлестірілу заңдарының бірі. ЫТ кейбір [ a, b ] интервалында тұрақты б. т., бұл константаның мәні нормалаудың (4. 2) шартына сәйкес 1 /( b- a) тең, ҮФ [ a, b ] интервалында 0-ден 1-ге дейін сызықты түрде өседі. Математикалық үміт кездейсоқ шаманың болуы мүмкін мәндер интервалының ортасына тең екендігін көрсетуге оңай.
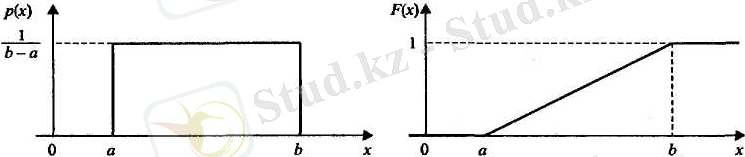
5 сурет - Үлестірімі бірқалыпты кездейсоқ шаманың ЫТ мен ҮФ-сы
Нормаль үлестірілу
Кездейсоқ шамалар үлестірілуінің нормаль заңы (normal distribution, Gaussian distribution) талдау үшін өте ыңғайлы және іс жүзінде жиі кездеседі, әсіресе ол байланыс арнасының бөгеулеріне тән. Нормаль кездейсоқ шаманың БЫТ мына өрнекпен анықталады:
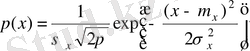 , (4. 11)
, (4. 11)
мұндағы т х пен σ х 2 - процестің математикалық үміті мен дисперсиясы, сәйкесінше.
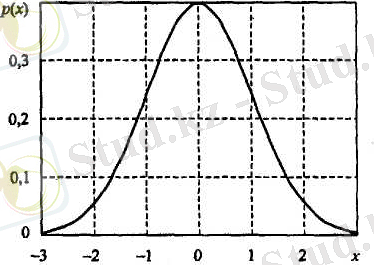
6 сурет - Үлестірімі нормаль ( т х =0 және σ х = 1) кездейсоқ шаманың ЫТ-ы.
Үлестірілудің нормаль заңының табиғатта кең тарағаны саны жеткілікті жоғары, ықтималдықтарының үлестірілу тығыздығы кез келген, қуаты бірдей статистикалық тұрғыдан тәуелсіз кездейсоқ шамалар қосылғанда, қосындының үлестірілу тығыздығы нормаль заңына ұмтылатынымен байланысты. Бұл тоқтам центрлік шекті теорема д. а.
НҮ-ң математикалық талдау үшін өте пайдалы қасиеті - гаустің кездейсоқ шамалары корреляциясыз және статистикалық тұрғыдан тәуелсіз б. т.
MatLab-та КП-ң ЫТ анықтау үшін pdf функциясы қолданылады:
p=pdf(‘name’, Х, A1, A2, A3),
мұнда 'name' мәтіндік параметрі үлестірілудің атын білдіреді, мысалы ‘norm‘, ‘unif‘, ‘exp‘, ‘bino‘, ‘beta‘, т. с. с., А1, А2 - үлестірілудің параметрлері, олардың саны мен мағыналары әр түрлі үлестірілулер үшін әр түрлі болады (мысалы, нормаль үлестірілу үшін ол m x пен σ x ) , мұндай үлестірілумен бірмәнді түрде анықталатын (берілетін) КП-ң Х векторындағы мәндерді алудың ықтималдықтары р векторына жазылады, р векторының ұзындығы Х векторының ұзындығындай болады.
Pdf функцияны шақырудың басқа түрі: p=normpdf(Х, A1, A2) . Мұнда да norm орнына unif, exp, bino, т. с. с. қолдануға болады.
ЫҮФ есептеу үшін сdf операторы қолданылады, оның форматы pdf-ң форматындай болады.
Іс жүзінде КП үлестірілуінің түрі әдетте белгісіз болады. Бұл жағдайда процесс эргодикалық деп болжап, ықтималдықты бағалау үшін N=hist(Y, M) деген операторды пайдалануға болады. Егер М - скаляр болса, онда кездейсоқ процестің реализациясын білдіретін Y векторының мәндер аймағы М бірдей интервалдарға бөлінеді де, ұзындығы М-ге тең N векторына Y элементтерінің әр интервалға түскен саны жазылады. Егер М - вектор болса, онда бұл оператор Y элементтерінің центрлері М векторында берілетін интервалдар бойынша үлестірілуін береді.
КП-ң орташа мәні мен дисперсиясын, егер ЫҮ-ң түрі белгілі болса, форматы мынадай операторлар көмегімен анықтауға болады:
[m, v] =unifstat(a, b) .
unif орнына norm, exp, т. с. с-ларды қолдануға болады. Кіріс аргументтер ретінде үлестірілудің параметрлері қолданылады.
Нақты физикалық процестер жағдайында, үлестірілу түрі белгісіз болса, процес эргодикалық деп болжап, орташа мән, дисперсия және орташа квадраттық ауытқуны бағалау үшін mean(x), var(x) және std(x) операторлар сәйкесінші қолданылады.
Кездейсоқ процестің корреляциялық функциялары
ЫБТ мен онымен байланысты сандық сипаттамалары КП-ң қасиеттері туралы маңызды мәліметті алуға мүмкіндік береді. Бірақ көптеген есептерді шешу үшін олар жеткіліксіз болады, өйткені ол X(t) КП туралы тек бөлек мезеттердегі мәлімет береді де, бұл процесс уақытта қалай өзгеретіні туралы ештеме айтпайды, КП-ң әр түрлі мезеттердегі мәндерінің статистикалық байланысын еске алмайды. КП-ң уақыттық сипаттамаларын бейнелеу үшін біргелік ықтималдықтың тығыздығы деген ұғым енгізіледі, ол бір мезгілде бірнеше шарт орындалуының ықтималдығын анықтайды.
Мысалы, КП-ң кез келген t 1 және t 2 мезеттердегі екі қимасы болсын (1 суретті қара), бұл қималардың жиынтығы {X(t 1 ), X(t 2 ) } екіөлшемді кездейсоқ шаманы тізеді, бұл шама р(х 1 , х 2 , t 1 , t 2 ) ықтималдықтың екіөлшемді тығыздығымен сипатталады. р(х 1 , х 2 , t 1 , t 2 ) dх 1 х 2 көбейтіндісі X(t) КП-ң жүзеге асырылуының t 1 уақыт мезетінде х 1 маңайындағы ені dx 1 интервалға, ал t 2 уақыт мезетінде х 2 маңайындағы ені dx 2 интервалға түсуінің ықтималдығын береді:
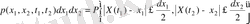
Ықтималдықтың екіөлшемді тығыздығының жалпылауы - КП n -өлшемді қимасы мен р(х 1 , х 2 , …, x n , t 1 , t 2 , …, t n ) ықтималдықтың n -өлшемді тығыздығы. n шексіздікке ұмтылғанда ( п → ∞ ) мұндай функция КП-і толығымен сипаттайды.
Енді стационар процестің анықтамасын нақтылайық. Егер КП ықтималдығының көпөлшемді тығыздығы (кезкелген n үшін) барлық t 1 , t 2 , . . . , t n уақыттық қималарың бірдей τ шамаға ығыстырғанда өзгермесе, бұл КП қатаң стационар , не тығыз мағынада стационар деп а.
р(х 1 , х 2 , …, x n , t 1 , t 2 , …, t n ) = р(х 1 , х 2 , …, x n , t 1 + τ, t 2 + τ, …, t n + τ) қайсы бір τ үшін .
Ал егер мұндай ығысу кезінде тек бірөлшемді мени екіөлшемді ықтималдықтар тығыздығы өзгермесе, бұл процесс кең мағынада стационар б. т. дейді. Тығыз мағынада стационар процес кең мағынадада стационар болатыны, ал кең мағынадағы стационарлықтан процестің қатан стационарлығы шықпайтыны түсінікті.
КП ықтималдығының көпөлшемді тығыздығын табу әдетте қиыншылыққа соғады, бірақ көптеген есептерді тек екіөлшемді ықтималдықтар тығыздығы негізінде шешуге болады.
Оның ішінде, р(х 1 , х 2 , t 1 , t 2 ) екіөлшемді ықтималдықтар тығыздығын білу КП-ң өте маңызды сипаттамасы болып табылатын ковариациялық функциясын табуға болады.
K x (t 1 , t 2 ) = M{x(t 1 ) x(t 2 ) } .
Бұл анықтама бойынша X(t) кездейсоқ процестің ковариациялық функциясы X(t) кездейсоқ функцияның t 1 және t 2 уақыт мезеттеріндегі мәндерінің статистикалық орташа көбейтіндісіне тең.
Кездейсоқ процестің әр жұзеге асырылуы үшін х(t 1 ) х(t 2 ) көбейтіндісі кейбір сан болып табылады. Жүзеге асырулардың жиынтығы үлестірілуі екіөлшемді ықтималдықтың тығыздығымен сипатталатын кездейсоқ сандардың жиынын құрайды. Бұл ықтималдық тығыздығы белгілі болса, жиын бойнша орташалау операциясы мына формула көмегімен жасалынады:
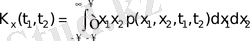
Кездейсоқ процестерді талдау кезінде олардың флуктуациялық құраушысы жиі қызықты болады. Мұндай жағдайларда корреляциялық функция қолданылады. Ол центрленген кездейсоқ функцияның (X(t) -m x (t) ) t 1 және t 2 уақыт мезеттеріндегі мәндерінің статистикалық орташа көбейтіндісіне тең:
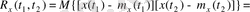
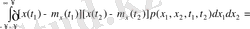
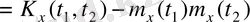 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz