Сүзілудің сызықтық заңы бойынша бірөлшемді сығылмайтын сұйықтықтың тұрақтанған ағымдары

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

Жоспар

Кіріспе . . . 1

Дарси заңы . . . 4

1. 1. Сүзілудің жалпы теориялық заңы . . . 7

1. 2. Кеуекті ортадағы сұйықтықтың бірөлшемді тұрақтанған ағымдары. 10

1. 3. Сығылмайтын сұйықтықтың бірөлшемді ағымдарының

салыстырмалы талдауы . . . 14

1. 4. Сығылмайтын сұйықтықтың бірөлшемді сүзілу ағымдары . . . 15

Пайдаланылған әдебиеттер . . . 17

Кіріспе

Жерасты гидромеханикасы сұйықтықтардың, газдардың және олардың қоспаларының кеуекті және жарықшақты тау жыныстарында сүзгіленуі туралы ғылым болып табылады. Сүзгілеу ағымы, яғни кеуекті немесе жарықшақты ортадағы сұйықтықтың (газдың, газ бен сұйықтықтың қоспасының) ағымы жерасты гидромеханикасының объектісі болып табылады. Жерасты гидромеханикасы мұнай және газ кенорындарын игеру және мұнайгазды алу технологиясы теориясының құрам бӛлігі болып табылады. Жерасты гидромеханикасының заңдарын білу берілген қабат жағдайы үшін кенді игерудің ұтымды режимдері мен жүйелерін таңдауда қажет. Кенді игерудің гидродинамикалық модельдеуі жерасты гидромеханикасының тура есебін шешу шегінде алынған және сүзгілену үрдісін нақты жағдайда сипаттайтын математикалық теңдеулерді пайдалануға негізделген. Қабаттың сүзгілену сипаттамаларын анықтау мақсатымен игеру үрдісін бақылау және реттеу үшін қабаттардың және ұңғылардың гидродинамикалық зерттеулерін жүргізеді. Бұл зерттеулерді мәліметтерін ӛңдеуі жерасты гидромеханикасының кері есебін шешуге негізделген. Жерасты гидромеханикасы басқа ғылымдарда да кең қолданылады: гидрогеологияда, инженерлік геологияда, гидротехникада, т. б. Судың қаныққан грунттарда сүзгіленуін зерттеудің алғашқы тәжірибелерін француз ғалымы А. Дарси жүргізген. Ол 1856 ж. сүзгілену жылдамдығының қысым градиентінен тәуелділігін кӛрсететін эксперименталдық заңын тұжырымдаған. Осы жылдары басқа француз ғалымыЖ. Дюпюи монографиясын жариялаған. Онда грунт суларының сүзгілену теориясы келтірілген, құдықтар дебиттерінің формулалары шығарылған және сүзгілену есептері шешілген.

Жерасты гидромеханикасының дамуына Ч. Слихтер және М. Маскет атты америкалық ғалымдар да айтарлықтай үлесін қосқан. Сүзгілену теориясының ресей мектебінің негізін қалаушылар - профессор Н. Е. Жуковский және академикН. Н. Павловский, ал ресейлік мұнайгаз жерасты гидромеханикасының негізін қалаушысы - академикЛ. С. Лейбензон. Сонымен қатар, мұнайгазсу қабаттарындағы сұйықтықтар мен газдардың сүзгілену теориясынаС. А. Христианович, Б. Б. Лапук, И. А. Чарный, В. Н. Щелкачев, т. б. зор үлесін қосқан.

1. Дарси заңы

Дарси заңы - сүзілу жылдамдығының су тегеуріні бәсендеуіне пропорционалдығы заңы.

$Q = K_{c}\frac{\mathrm{\Delta}h}{L}F$

Бұл заңды алғаш рет тәжірибе жүзінде құмды сүзгідегі су ағынын зерттеу барысында француз инженері А. Дарси (1856 жылы) ашқан. Сүзілу кезіндегі тегеурін шығынының жылдамдыққа тәуелділігі түзу сызықты болғандықтан, Дарси заңы сүзілудің түзу сызықты заңы деп те аталады. Дарси заңы ағынның ламинарлық режімі жағдайындағы кеуекті ортадағы сұйықтықтың сүзілу заңы Дарси заңы бойынша сүзілу жылдамдығы ( v {\displaystyle v} v) пъезометрлік көлбеудің ( i {\displaystyle i} i) шамасына тура пропорционал: v = k i {\displaystyle v=k_{\mathrm {i} }} v=ki мұндағы k {\displaystyle k} k- көлбеуі бірге тең жағдайда сан жағынан сүзілу жылдамдығына тең болатын сүзілу коэффициенті, өлшем бірлігі см/сек., k {\displaystyle k} k-ның сандық мәні топырақтың сипатына және ең алдымен оның кеуектерінің шамасына тәуелді. Дарси заңының Дюпий формуласынан ерекшелігі сол: козғалыстың кез келген сипатындағы (бірқалыпты немесе күрт өзгеретін) сүзілу аймағындағы кез келген нүктенің сүзілу жылдамдығын анықтайды. Дарси заңы бойынша сүзілу жылдамдығы қысым градиентіне тура пропорциональды. Өткізгіштік коэффициенті кеуекті ортаның қасиеттеріне ғана тәуелді және сұйықтықтың қасиеттеріне ғана тәуелді. Өткізгіштік коэффициентін эксперименталды жол мен ішінде топырағы бар арнайы аспап - пермеаметрдің көмегімен анықталады

к/м - жылжымалық коэффициент

Өткізгіштің өлшем бірліктері СИ жүйесінде $м^{2}$ ; ${мкм}^{2}$ ;

ал СГС жүйесінде - Д(Дарси) ; мД; 1Д $=$ 1, 02 $\bullet 10^{- 12}$ м $=$ 1 ${мкм}^{2}$

Өтімділік коэффициенті. Дарси заңындағы, яғни сүзбеленудің бағдарлы заңындағы пропорциялық коэффициент. Бұл коэффициенттің бірлігі ретінде кеуекті ортадан алынған ауданы 1 м3, ұзындығы 1 м үлгі арқылы қысым мөлшері 0, 1 мПа-ға, сұйықтық шығыны 1 м3/сек-ке өзгергендегі тұтқырлығы 1 мПа сәйкес келетін сол кеуекті орта өтімділігі алынады.

Ағын - табиғаттағы су айналымы процесінің нәтижесінде судың жер бетімен және оның астымен ағуы. Беткі және жер асты ағыны болып екіге бөлінеді:
Беткі ағын өз алдына беткейлік және арналық болып ажыратылады. Ағын мөлшері және режимі жауын-шашын мен булану мөлшеріне, ауа температурасы, жер бедері, геологиялық құрылысы, топырақ пен өсімдік сипатына байланысты қалыптасады. Ағынның келесі екі мағысы бар:
- өзендегі немесе өзге де су арналарындағы сумассасының көлденең кеңістікті түгел қамтитын қозғалысы;
- жалпы қозғалысты бейнелейтін түсінік (мысалы, су ағыны, ауа ағыны, т. б. )
Ағын аймақтың климат жағдайына тәуелді. Ағынның жалпы шамасы - су шығымы, ағын модулі, ағын коэффициенті және ағын су қабатының қалыңдығы деп аталатын элементтер арқылы анықталады.

Өсімдіктердің, жануарлардың (әсіресе микроорганизмдердің), климат жағдайларының және адамдардың әсерімен өзгерген жер бетінің үстіңгі борпылдақ қабаты. Топырақ бойында құнарлылық қасиеті, яғни өсімдіктерді сумен, басқа да қоректік элементтермен қамтамасыз ететін қабілеті болады. Механикалық құрамы (топырақ түйіршіктерінің мөлшері) бойынша топырақ құмды, құмдақ сазды және саз топырақ болып бөлінеді. Жасы мен генезисі бойынша - қыртысты күлгін топырақ, батпақты топырақ, ормандық сұр топырақ, қара топырақ, қоңыр топырақ, күрең топырақ, тағы басқалар болып бөлінеді. Топырақтың жер бетінде таралуы зоналық (горизонтальды және вертикальды) заңдылыққа байланысты.

Топырақ - литосфераның жоғарғы әуе қабатымен байланысатын қабат, бүкіл биосферадағы тіршіліктің тірегі. Топырақ ғасырлар бойы топырақ түзуші факторлардың үздіксіз әрекетінен пайда болған табиғаттың ерекше табиғи, әрі тарихи денесі.

Құм- ұсақ түйірлі борпылдақ шөгінді тау жыныстары. Пайда болу тегі жағынан құмдар көлдік, теңіздік, флювиогляциалдық (сулық-мұздық), элювийлік, делювийлік, пролювийлік және эолдық (желдік) топтарға бөлінеді.

1. 1. Сүзілудің жалпы теориялық заңы

Кеуек арналары қималарының пішіні мен ӛлшемі кеңістікте кенет және ретсіз өзгереді. Бұл тұтқыр сұйықтық ағысының теңдеуін дәл шешуін қиындатады. Сондықтан, кеуекті кеңістіктің алғашқы теориялық зерттеулері идеалдандырылған модельдердің кӛмегімен жүргізілген. Мұндай модельдері ретінде идеалды және жалған грунттар алынған. Кеуектің арналары параллельді осьтері бар жіңішке цилиндртәрізді түтіктерінің (капиллярларының) шоғыры болып табылатын кеуекті ортаның моделін идеалды грунт деп атайды. Диаметрі бірдей шартәрізді бӛлшектерінен тұратын және нақты грунттың болашақ бейнесі болып табылатын кеуекті ортаның моделін жалған грунт деп атайды. Идеалды грунттың моделі құбыр гидравликасының заңдылықтарынан сұйықтықтың жалған, содан кейін нақты грунттарда жылжуына ауысу үшін пайдаланылған. Тұтқыр сұйықтық құбырбойымен жылжығанда екпіннің гидравликалық жоғалымдары Пуазейльдің формуласымен анықталатыны мәлім:

$\mathrm{\Delta}h = \ \frac{32 \bullet \mu \bullet \mathrm{\Delta}L \bullet V}{\rho \bullet gD^{2}}$ (1. 1)

Мұндағы: $\mathrm{\Delta}h$ - ұзындығы, $\mathrm{\Delta}L - учаскесіндегі\$ екпіннің үйкеліске кететін жоғалымдары; $\mu$ - сұйықтықтың динамикалық тұтқырлығы; $\rho$ - сұйықтықтың тығыздығы; D - құбырдың диаметрі.

Құбырдың көлденең қимасының ауданың $\int_{}^{}.$ деп белгілейік:

∫ $\ = \ \frac{\pi D^{2}}{4}$

теңдеуін келесі түрде жазайық:

$\mathrm{\Delta}\rho = \ \frac{32 \bullet \pi \bullet \mu \bullet \mathrm{\Delta}L \bullet V}{4\int} = \ \frac{8 \bullet \pi \bullet \mu \bullet \mathrm{\Delta}L \bullet V}{\int}$

$\rho$ g $\mathrm{\Delta}$ h $= \mathrm{\Delta}P$ болғандықтан ( $\mathrm{\Delta}P - \mathrm{\Delta}L$ ұзындығындағы қысымның сарқырамасы)

Келесі теңдеу шығады:

$\mathrm{\Delta}p = \$ $\frac{8 \bullet \pi \bullet \mu\mathrm{\Delta}L \bullet V}{\int}$ .

Осыдан жылдамдықты шығарайық:

V $=$ $\frac{\int \bullet \mathrm{\Delta}\rho}{8 \bullet \pi \bullet \mu \bullet \mathrm{\Delta}L}$ (1. 2)

Бұл құбыр немесе идеалды грунт үшін дұрыс формула болады. Идеалды грунттан жалған грунтқа ауысу үшін, біркеуекті арна қимасының fауданын жалған грунт саңылауларының fауданымен байланыстырып, кеуекті кеңістіктің пішінін есепке алу керек. Мұны кеуек арналарының қималарын геометриялап және шартәрізді бӛлшектерді орналастырудың тығыздығын (60°≤θ≤90°) кеуектілік арқылы кӛрсетіп жасауға болады. Нәтижесінде бірқатар зерттеушілер сұйықтықтың жалған грунтта сүзілу заңының біртекті формулаларын алған:

Q $\ =$ $\frac{d^{2\ } \bullet F \bullet \mathrm{\Delta}P}{96 \bullet \sigma \bullet \mu \bullet \ \mathrm{\Delta}L}$

мұндағы: F - кеуекті орта қимасының ауданы; d - бөлшектер диаметрі.

1. 2. Кеуекті ортадағы сұйықтықтың бірөлшемді тұрақтанған ағымдары

Қабат флюидтерінің сүзгілену нақты үрдістерінің ӛте күрделі болатындығынан ұқсас физикалық немесе геометриялық модельдерді тұрғызу мүмкін емес. Сондықтан, кӛптеген жағдайда сүзгілену ағымдарының жуықтаған модельдеуімен шектеледі. Ол мұнай және газ кенорындарын игеру үрдісінің шынайы математикалық сипаттауын қамтамасыз етуге мүмкіндік береді. Бұл үрдісті жеңілдетілген (идеалдандырылған) модельдерде зерттеуге болады. Модель ретінде тұрақтанған немесе тұрақтанбаған режимдердегі бірӛлшемді немесе көпөлшемді сүзгілену ағымдарының сызбаларын алуға болады. Табиғи қабаттардағы сұйықтық пен газдың сүзгілену ағымдарын зерттеген кезде есептеу сызбаларын құруға, негізгі эффектілерін есепке алуға және ағымның параметрлерін анықтауға мүмкіндік беретін қозғалыстың геометриялық түрін сызу керек. Қарапайым сүзгілену ағымдарын зерттегенде жерасты гидромеханикасында біртекті (изотроптық) кеуекті ортадағы бірфазалық флюидтердің (сығылатын немесе сығылмайтын) тұрақтанған немесе тұрақтанбаған сүзгіленуінің модельдері негізгі болып табылады. Бірақ табиғи қабаттардағы сұйықтықтардың, газдардың және олардың қоспаларының сүзгіленуінің күрделі бірӛлшемді емес есептерін шығару қажеттілігі мұнай кенін игеру кезінде жүретін гидродинамикалық және физикалық-химиялық үрдістерді біліп түсінуге негізделген математикалық модельдерді құруды талап етті. Әдетте, бұл модельдерді қолдану сандық әдістер мен қазіргі заманғы есептеу техникасын қолданумен байланысты. Гидродинамикалық есептерді шешкенде жазық ағым квазибірөлшемді ағыммен аппроксимацияланады. Ол үшін сүзілудің барлық аймағы сұйықтықтың ағысы бірӛлшемді болып саналатын шартты түрде бірнеше шағын аймақтарға бөлінеді.

Сүзілу жылдамдығы мен екпіні (қысымы) ағыс бойымен саналатын бір ғана координатаның функциялары болып табылатын сүзілу ағымы бірӛлшемді деп аталады. Бірөлшемді сүзілу ағымдарының үш түрі бар. Оларды қарапайым әдістердің кӛмегімен толық зерттеуге болады:

1) тік сызықты-параллельді;

2) жазықрадиалды;

3) радиалды-сфералық.

Тік сызықты-параллельді. Тік сызықты-параллельдіағым сұйықтық немесе газ цилиндрлік кен арқылы оның осіне параллельді аққанда зертхана жағдайында, сонымен қатар қоректену контуры біржақты созылмалы қабаттарда кездеседі. Тік сызықты-параллельдіағым сұйықтықтың барлық бөлшектерінің траекториялары тік сызықты болғанда, ал ағымның кӛлденең қимасының кез келген нүктелерінде сүзілу жылдамдықтары бір-біріне тең болғанда орынды.

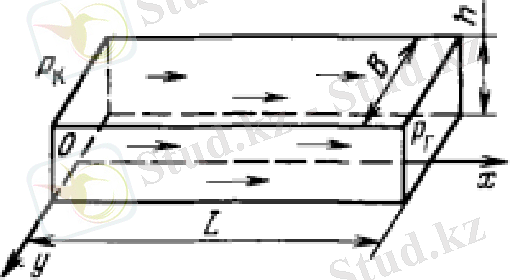
3. 1- сурет. Ағымның тік сызықты-параллельді сүзілудің сұлбасы.

Рк және Рг-қоректену контурындағы қысым. Табиғи жағдайға және игеру жүйесіне байланысты қоректену контуры ретінде мыналар алынады: а) беттік сулармен толатын қабат шығуына сәйкес келетін сызық. Бұл жағдайда Рк қоректену аймағындағы су бетінің деңгейіне () байланысты анықталады; б) шартты айдау аймағы, яғни айдау ұңғыларының торды тығыздау шегі болып табылатын абстракция. Мұнайды өндіру галереясы қабаттан өндіру аймағы болып табылады. Бұл өндіру ұңғыларының тығыздау шегі болып табылатын абстракция.

Жазық радиалды ағым. Ағымның бұл түрі сұйықтық немесе газ бір нүктеде радиалды қосылатын көлденең тік сызықты траекториялармен бір жазықтықта қозғалатын жағдайларда орынды болады. Мысал ретінде, ортасында қабат түбі ашық және қабатты барлық қалыңдығына ашатын бір ұңғысы бар қалыңдығы тұрақты және шексіз созылатын көлденең қабатта сұйықтықтың қозғалысын қарастыруға болады. Радиалды-сфералық ағым. Ағымның бұл түрі ұңғы қабаттың төбесін ғана ашқанда немесе ашу тереңдігі қабат қалыңдығынан едәуір кіші болса ғана орынды. Сонымен бірге, сұйықтықтың немесе газдың барлық бөлшектерінің қабаттағы қозғалыс-тарының траекториялары тік сызықты және жартылай сфералық қабат түбінің ортасында радиалды қосылған болады.

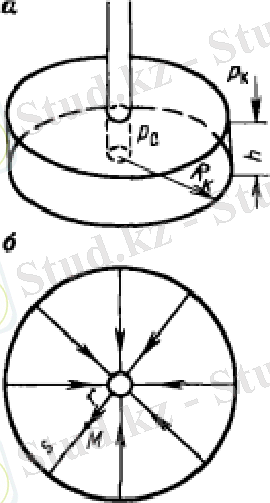
3. 2-сурет. Ағымның жазық-радиалды сүзілу сұлбасы. А-жалпы түрі; в-жоспар

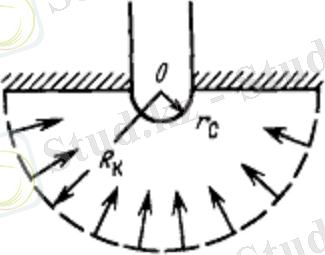
3. 3-сурет. Ағымның радиалды-сфералық сүзілу сұлбасы

Ағымдардың барлық түрлері бір өлшемділерге жатады, өйткені қысым мен сүзілу жылдамдығы бір ғана координатаның (сызықты немесе радиустың) функциялары болып табылады.

1. 3. Сығылмайтын сұйықтықтың бірөлшемді ағымдарының салыстырмалы талдауы

Екі негізгі сүзілу ағымдарының (тік сызықты-параллельді және жазық радиалды) сипаттамаларын тӛмендегі жағдайларға байланысты қарастырайық:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.