Сигналдарды талдау міндеттері

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Сигналдарды талдау міндеттері

Сигналдарды өңдеу не үшін қажет? Сигнал кейбір информацияны тасымалдайтын физикалық шама болып табылады. Бірақ сигналда әдетте бөгеулер де болады. Сигналды өңдеу сол бөгеулерді алып тастап, керекті информацияны бөліп алу үшін қажет болады екен. Яғни сигналдарды өңдеу ластанған суды тазартуға ұқсайды, бұл тазартудың негізгі мақсаты - суда бар болған элементтерді (құраушыларды) керекті мен керексіздерге ажыратып алу.

Талдау сигналды өңдеудің түйінді компоненттерінің бірі болып табылады. Талдаудың үш негізгі құраушысын бөлуге болады:

сигналдың сандық параметрлерiн анықтау;
сигналды элементар құраушыларға жiктеу (бұл жіктеу сигнал құраушыларды жеке қарастыру үшін, немесе басқа сигналдың қасиеттерімен салыстыру үшін жасалынады) ;
әртүрлi сигналдардың “ұқсастығы” дәрежесiн санды түрде өлшеу.

Кейбір объектпен жіберілетін сигналды талдау бұл объекттің қасиеттері, сол қасиеттердің өзгеру себептері туралы мәлімет береді, бұл объекттің бақыланып отырған өзгерістерінiң себептерiн айқындап, оның кейiнгi даму жолдарын болжауға мүмкiндiк бередi.

Сигналдар классификациясы

Сигнал деп жалпы жағдайда бiр шаманың басқа шамаға тәуелдiлiгiн айтады, яғни математикалық тұрғыдан сигнал функция б. т.

Әдетте тәуелсіз шама болып уақыт табылады, бірақ ол басқа да болуы мүмкін. Мысалы, информацияның оптикалық өңдеу жүйелерінде жарық қарқындылығының кеңістіктік координаталарға тәуелділігі сигнал ретінде қарастырылады. Телевизиялық бейнені де сигнал деп санауға болады, мұнда экранның нүкте жарықтылығының координаталарға тәуелділігі қарастырылады. Бұл екі тәуелсіз шамасы бар сигналдың мысалы. Мұндай сигналдаржы екіөлшемді д. а.

Сөйтіп, сигналдың физикалық табиғаты кез-келген бола алады, жиі ол кернеу болады, басқа да көптеген физикалық шамалар болуы мүмкін. Сондықтан курс мазмұнымен танысу физиканың кез-келген саласында тиiмдi ғылыми жұмыс жасауға көмек көрсетедi.

Сигнал дәлме-дәл белгілі болуына, не болмауына байланысты детерминді және кездейсоқ сигналдарды бөледі.

Детерминді сигнал толығымен белгілі болады, оның кезкелген уақыт мезетіндегі мәнін дәлме-дәл анықтауға болады.

Кезлейсоқ сигнал кезкелген уақыт мезетінде кездейсоқ шама б. т., ол анықталған мәндерді кейбір ықтималдықпен алады. Дәл айтқанда, кез келген нақты сигнал кездейсоқ б. т., өйткені оның қалыптасуына көптеген факторлар әсер етеді, олардың барлығын еске алуға мүмкін емес.

Сигналдардың өте маңызды класы - квадраты интегралданатын сигналдар. Басқаша оларды энергиясы шектелген сигналдар д. а. Мұндай сигналдар үшін мынадай қатынас орындалады:

Сигналдар теориясының көптеген маңызды қатынастар сигналдардың энергиясы шектелген деген болжау шегінде алынған. Егер бұл шарт орындалмаса, мәселені шешу үшін басқа тәсілдерді пайдалану қажет болады.

Тағы бір талдау әдістерге елеулі әсер ететін классификацияның белгісі - периодтылық. Мұндай сигналдар үшін кез-келген t үшін s(t + пТ) = s(t) деген қатынас орындалады, мұндағы п - кез-келген бүтін сан. Т шамасы мен оған еселі 2Т, ЗТ, т. с. с шамалар сигналдың периодтары болып табылады, бірақ әдетте период деп олар ішіндегі минимал мәнін айтады, оны басқаша негізгі период деп атайды.

Периодқа кері шама сигнал қайталуының жиілігі деп аталады: f = 1/T. Жиі циклдік (дөңгелектік) жиілік ұғымы қолданылады: ω=2πf , [ ω ] = рад. /с.

Кезкелген периодты сигналдың энергиясы шексіз болатыны түсінікті (әрине, егер сигнал теңбе-тең нольге тең болмаса) .

Сигналдарды өңдеу техникасында маңызды роль атқаратын гармониялық тербелістер периодтыларға жатады:

s(t) = A cos(ω t + ϕ) .

Келесі класс - ұзақтығы шектелген сигналдар, басқаша оларды финитті, немесе шекті тасушыда анықталған сигналдар д. а.

Егер мұндай сигналдың екінші текті үзілістер болмаса, оның энергиясы шектелген болатыны анық.

Ұзақтығы шектелген сигналдардан импульсті мен өшетін сигналдарды бөлуге болады. Импульсті сигналдардың энергиясын уақыттың қысқа интервалында бөлінеді. Өшетін сигналдар - энергиясы шектелген, уақыттың жеткілікті ұзақ аралығында жоққа айналатын сигналдар.

Импульсті сигналдарға өте маңызды, тесттік (тексергіш) сигнал ретінде қолданатын дельта-функция да жатады. Дельта-функция δ (t), немесе Дирак функциясы, - функция аргументі нөлге тең болған нүктеде орналасқан амплитудасы шексіз жоғары шексіз қысқа импульс. Импульс «ауданы» 1-ге тең:

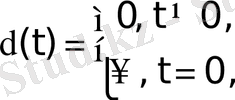
1 сурет. s(t) = δ(t) + 2δ (t - 1) сигналының графигі

Дельта-функция сүзбелеу қасиетке ие :

Дельта-функция өлшемділігі оның аргументының өлшемділігіне кері.

σ(t) бірлік секірме функциясы да (ол Хевисайд функциясы, қосу функциясы деп те аталады) радиотехникада өте маңызды болып табылады:

Рис. 2. Бірлік секірме функциясы

АНАЛОГТЫҚ, ДИСКРЕТТІК ЖӘНЕ ЦИФРЛІК СИГНАЛДАР

Алғашқы физикалық сигнал әдетте уақыттың үздіксіз функциясы болып табылады. Мұндай, уақыттың барлық мезеттерінде анықталған сигналдар аналогтық (analog) деп аталады.

Сигналдың цифрлік өңдеуі кезінде сигнал дискреттік қатар (discrete series) болып табылатын сандар тізбегі түрінде беріледі де, аналогтық сигналға толығымен сай келе алмайды. (Егер сигналдың аргументі уақыт болса, мұндай қатар уақыттық қатар деп талады) . Тізбекті құрайтын сандар сигналдың жеке (дискретті) уақыт мезеттеріндегі мәндері болып табылады да, сигналдар санақтар ы (samples) деп аталады. Әдетте санақтар дискреттеу периоды (немесе дискреттеу аралығы, қадамы - sample time) деп аталатын уақыттың бірдей аралықтарынан кейін алынады. Дискреттеу периодына кері шама дискреттеу жиілігі (sampling frequency) деп аталады: f _Д = 1/Т . Оған сай дөңгелектік жиілік: ω _Д = 2π /Т.

Аналогты сигналды санақтар тізбегіне түрлендірі процесі дискреттеу (sampling) деп, ал бұл түрлендірудің нәтижесі - дискреттік сигнал деп аталады . Дискреттеу уақыт (немесе басқа тәуелсіз айнымалы) бойынша да, сигналдың мәні бойынша да өткізіле алады . Бірінші жағдайда ол таңдама алу операциясы , немесе жай дискреттеу деп, ал екінші жағдайда - кванттау (деңгей бойынша кванттау) (quantization) деп аталады, кванттау кезінде пайда болатын жуықтау қателіктері кванттау қателіктері (немесе шуылы) (quantization error, quantization noise) деп аталады.

Уақыт бойынша дискреттелген, бірақ деңгей бойынша квантталмаған сигнал дискретті (discrete-time) сигнал деп аталады. Уақытта да дискреттелген, деңгей бойынша да квантталған сигнал цифрлік (digital) сигнал деп аталады. Деңгей бойынша квантталған, бірақ уақытта үздіксіз сигналдар іс жүзінде сирек кездеседі.

1 сурет. Аналогтық (сол жақта), дискреттік (центрде) және

цифрлік (оң жақта) сигналдар

Аналогтық сигналдың цифрлікке түрлендіруі аналогты-цифрлі түрлендіргіш (АЦП; Analog-to-Digital Converter, ADC) көмегімен жүзеге асырылады.

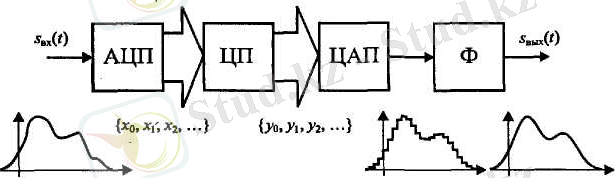
2 сурет. Сигналдардың цифрлік өңдеу жүйесінің құрылымдық сүлбесі.

Компьютерлік өңдеуді тек цифрлік сигналдар үшін жасауға болады. Бірақ біз көбінесе дискретті сигналдар мен оларды өңдеу әдістерін қарастырамыз, өйткені кванттамен байланысты эффектерді көбінесе еске алмауғаболады: кванттау қателіктері мәліметтерді жинау мен өңдеу барысында пайда болатын басқа қателіктерден айтарлықтай аз болады. Бірақ егер үздіксіз кіріс сигнал кванттау шкаласының аз бөлігін алса, кванттау қателігі елеулі болады. Сондықтан үздіксіз процес мәндерінің өзгеріс диапазоны кванттау шкаласының айтарлықтай бөлігін алғанына ұмтылу керек.

Найквист жиілігі. Котельников теоремасы

Сигналдарды өңдеу кезіндегі маңызды мәселелердің бірі - дискреттеу периодын таңдау мәселесі. Жалпы жағдайда сигналды дискретті санақтар жыйынтығымен беру информацияның жоғалуына әкелетені анық, өйткені біз сигналдың санақтар арасындағы жүрісі туралы ешнәрсе білмейміз. Неғұрлым дискреттеу периоды көп, ал кванттау өрескел болса, соғұрлым сигналды көрсету үшін аз мәліметтер (берілгендер) керек болады (демек бұл мәліметтерді сақтау үшін керекті жадының көлемі мен оларды өңдеу үшін қажетті уақыт аз болады), бірақ сигнал сақтайтын информацияны жоғалтудың қауіпі көп болады.

Бірақ оларды дискреттеу информацияның жоғалуына әкелмейтін және өздерінің дискретті санақтар жыйынтығы негізінде толығымен алғашқы (аналогты) түрде қайта тұрғызыла алатын сигналдар бар екен.

Мысалы, гармониялық сигналды өның дискретті санақтары арқылы дұрыс беруге болады, бірақ ол үшін бұл сигналдың жиілігі дискреттеу жиілігінің жартысынан (бұл жиілікті Найквист жиілігі (Nyquist frequency) деп атайды: f _N = f _Д /2=1/(2Т), ω _N =ω _Д /2=π /Т ) көп болмау тиіс. Бұл шарт немен байланысты екенін 1 сурет түсіндіреді. Дискреттеліп отырған гармониялық сигналдың жиілігі мен Найквист жиілігі арасындағы қатынасқа байланысты үш жағдай болуы мүмкін:

Егер гармониялық сигналдың жиілігі Найквист жиілігіненкөпболса (былайша айтсақ, дискреттеу периоды гармониялық сигнал периодының жартысынан көп болса), дискретті санақтар негізінде (олар суретте дөңгелектермен көрсетілген) қайта тұрғызылған аналогты сигнал (ол пунктир сызықпен көрсетілген) сондай-ақ гармониялық болады, бірақ оның жиілігі өзгеше (төмен) болады (1в сурет) . Бұл эффектжалған жиіліктердің пайда болуы(немесежиіліктердің ауысуы, жасырынуы) (aliasing) деп аталады.

ЕСКЕРТУ

Периодты процестерді дискреттеу эффекттері айналыстағы объектердің (мысалы, автокөлік дөңгелектерінің) кино- не видеотүсіруі кезінде көрнекі түрде білінеді. Дискреттеу жиілігі (кадрлар ауысу жиілігі) жеткілікті жоғары болмағандықтан, тез айналатын дөңгелек қозғалмайтын не баяу айналатын (және де кезкелген жаққа) көрінуі мүмкін.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.