Бифуркациялық диаграммалар

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Бифуркациялық диаграммалар

Математикалық түрде біраз маңызды физикалық есептер параметрлерге байланысты дифференциалдық теңдеулерге сәйкес келеді. Параметрлердің өзгерісі қозғалыстың бір режимінің орнықтылығының жоғалтып, жүйенің басқа күйге өтуіне әкелу мүмкін. Мысал - параметр генерация табалдырығынан асқанда Ван-дер-Поль генераторында жаңа периодты қозғалыстың пайда болуы. Бұл құбылыс бифуркация деп аталады, ал ол болған кездегі параметрдің мәні - бифуркация нүктесі. Ең қажет бифуркациялар - бифуркация нүктесінен өткенде жүйеде қозғалыстың жаңа орнықты режимдерінің пайда болуы.

Жүйенің басқарушы параметрлерінің өзгеруімен бір орнықты күйдің басқамен ауысу иерархиясы бір дөрекі режим (құрылымдық орнықты) басқа дөрекі режимге фазалық өтулердің тізбегін тудырады және бифуркация нүктесінде дөрекі емес күй орындалады.

Бифуркацияның элементар теориясының математикалық негізі орнықтылық теориясы болып табылады. Орнықтылық және бифуркация теориясының көмегімен динамикалық жүйенің фазалық кеңістігін типтік траекторияларға бөлуді қарастыру, осы бөліктеудің құрылымдарын талқылау, параметрлер кеңістігінде шекті жиындардың сипаттаушы түрлері бар аумақтарын анықтау мүмкіндігі туады. Бұл параметрлері өзгергенде динамикалық жүйенің фазалық кеңістігінде қозғалыстың режимдерін қайта құру механизмдерін түсіндіретін бифуркациялық диаграмманы салуға мүмкіншілік береді.

Параметрлерді өзгерткенде периодтық мәндердің кездесуін бақылау керек. Хаостық қозғалыстың алғы хабаршының бірі субгармониялық периодты тербелістердің пайда болуы. Хаостың алғашқы күйі әртүрлі формада болуы мүмкін. Сандық та және де физикалық та тәжірибелер хаостың алғашқы күйінің бірнеше моделін анықтады.

Периодтың екі еселенуі арқылы хаосқа көшу . Периодтың екі еселену құбылысы байқалса кезде, бастапқы күйде жүйе негізгі периодты қозғалыста болады. Одан кейін тәжірибенің қандай-да r параметрін өзгерткенде бифуркация, немесе, периоды алғашқысынан 2 есе артатын периодты қозғалысқа ауысу байқалады. r параметірін әрі қарай өзгерткенде, жүйе тізбекті бифуркацияларға ұшырайды, әр бифуркация кезінде период екі еселенеді. Периодтың тізбекті екі еселенуі жүретін кезде r параметрінің “күдікті” мәні п → ∞ ұмтылғанда келесі автомодельді қатынасқа бағынады:

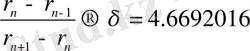. (8)

Бұл сан оны анықтаған адам құрметіне Фейгенбаум саны деп аталады. Іс жүзінде δ шамасы үшінші немесе төртінші бифуркацияда-ақ жинақталады. Периодтың еселену процесі белгілі бір параметрдің шекті мәнінде жиілеп, одан кейін хаосты қозғалысқа айналады.

Бұл қүбылыс бірқатар физикалық жүйелерде және сандық модельдеумен анықталған. Осындай сипат көрсететін қарапайым математикалық теңдеу - бұл бірөлшемді айырымдық теңдеу (логистикалық бейнелеу)

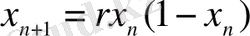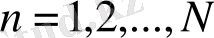, . (9)

r > 1 болған кезде логистикалық бейнелеу екі тепе-теңдік нүктесі бар (яғни, х = rx (1- х ) ) . х _n ₊₁ = f ( x _n ) бейнесінің орнықтылығын анықтау үшін тыныштық нүктесінде f '( x ) жанама мәнін табу керек. Егер f '( x ) > 1 болса, тыныштық нүктесі орнықты емес. Егер 1 < r < 3 болса логистикалық теңдеудің екі тыныштық нүктесі бар: х= 0, ( r -1) / r ; бұндағы координаттар басы орнықты емес, ал екінші тыныштық нүктесі орнықты.

Бірақ r = 3 болғанда х = ( r -1) / r кезіндегі жанама 1-ден асады ( f '= 2- r ) және тепе-теңдіктің екі нүктесі де орнықсыз болып кетеді. r параметрінің мәні 3 пен 4 аралығында болғанда қарапайым айырымдық теңдеу көппериодтық және хаостық қозғалысты сипаттайды. r = 3 болғанда орнықсыз стационарлық шешім болады, бірақ бицикл немесе екіпериодтық орбита орнықты болып қалады.

r мәнін ары қарай ұлғайтса екіпериодты орбита орнықтығын жоғалтады және периоды 4 тең цикл қалыптасады, ол бифуркациялар арқылы r -дың бұдан да үлкен мәндерінде периоды 8ге тең циклмен ауысады. Бұл периодтық екі еселену процесі r = 3, 56994 тең болғанға дейін жүреді. Осы мәннің төңірегінде еселену жүретін параметрлер мәндері (8) -нақты заңға бағынады.

Бифуркациялық диаграммалар. Логистикалық бейнелеудің бифуркациялық диаграммасын тұрғызу программасы және оның графигі (9-сурет) төменде келтірілген. 9-суретте келтірілген фазопараметрлік диаграмма хаосқа әкелетін периодтың екі еселену каскадты жүйесіне сәйкес. Диаграммалардың осындай түрі Фейгенбаум бұтағы деп аталады. Диаграмма динамикалық айнымалының масштабының бөлінуінің көрнекі мысалы, масштабтың скейлинг қасиеттерін көрсетеді, яғни көріністің бір элементі кішірек масштабта қайталана береді.

% Логистикалық бейнелеудің бифуркациялық

% диаграммасын салытын файлдың листингі

function Logotbr(rb, rh, N) ;

x = r*x*(1-x) ---

%параметрлер rb -бастапқы мәні r

% rh - қадам өзгерісі r

% N - қадам саны

clear;

%default values

rb = 0. 01;

rh = 0. 01;

N = 500;

% r соңғы мәнін есептейміз

rk = rh*(N-1) + rb;

% r береміз

r = [rb:rh:rk] ;

% x- тің бастапқы мәні

x(1:N) = 0. 1;

%- бейне аттракторға шығу үшін

%- 1000 қадам тастаймыз

for i = 1:1000

x = (1-x) . *x. *r;

end

%- енді нүктелерді саламыз

for i = 1:1000

% графикте нүктелер саламыз, (қара нүктелер)

plot(r, x, 'k. ') ;

% әзірше график шығарылмайды

hold on % жаңа терезе ашу режиміне тиым саламыз

% келесі нүктелерді есептейміз

x = (1-x) . *x. *r;

end

% нүктелерді бір жола саламыз (график шығарылады)

plot(r, x, 'k. ') ;

% x өсі үшін шектерді белгілейміз

xlim([2. 7 4. 1] ) ;

xlabel('r') ;

ylabel('x') ;

title('логистикалық бейнелеудің . . .

бифуркациялық диаграммасы') ;

логистикалық бейнелеудің бифуркациялық диаграммасы

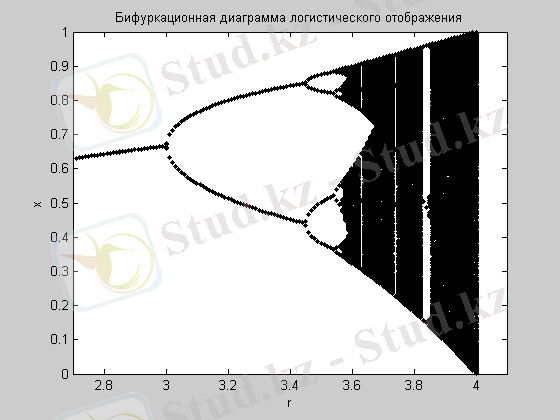
9-сурет. Логистикалық бейнелеудің бифуркациялық диаграммасы

Суретте периодтың екі еселенуі кезіндегі бифуркация нүктелері анық көрінеді, сол жерде бұтақ екіге бөлінеді. Жүйенің параметрі “күдікті” шамадан асып кетсе, белгілі параметрлер диапазонында қозғалыс хаосты болады, оған сәйкес аумақтар нүктелермен азды-көпті тығыздықпен толтырылған бұтақ басына ұқсайды. Бірақ осындай диапазондар шекті болады, басқаша айтқанда, параметр өзгергенде периодты қозғалатын “терезелер” кездесуі мүмкін. Осындай режимде периодты қозғалыстар қайта периодтың бифуркациялық еселенуіне ұшырап, хаосты қозғалысқа айналуы мүмкін.

Көптеген физикалық жүйелердің қасиеттері (3) -бейнелудің қасиеттеріне ұқсас болса да, әрбір жүйе өзінің ерекшелігін көрсетеді.

10-суретте Анищенко-Астаховтың инерциялық бейсызық генераторында (ИБГ) келесі теңдеулер арқылы

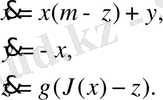(10)