Күн айналысы

Пән: Астрономия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Күн айналысы

Күннің өз өсі бойымен айналуы оның бойымен планеталардың айналу бағытында (демек Жердің өз осі боймен айналу бағытында да), Жер орбитасының жазықтығына (эклиптикаға) 7 ⁰ 15’бұрышпен еңкейген жазықтықта болады.

Күн өзінің масса центрі арқылы түзу бойымен айналады. Бұл оське перпендикуляр жазықтықты Күн экваторының жазықтығы немесе гелиоэкваторлық жазақтық деп атайды. Бұл жазықтықтың Күн бетімен қиылысу шеңбері гелиоэкваторы депатайды. Полюстерді қосатын Күн бетіндегі жарты шеңберлер гелиомеридиандар деп атайды. Күн бетіндегі берілген бір нүктенің гелиоендігі деп сол нүктенің радиус векторы мен гелиожазықтығы арасындағы бүрышты айтады. Сонда күн айналысы дифференциалды болып шықты. Атап айтсақ, күннің бетіндегі нүктелер айналыстың бұрыштық жылдамдықтары гелиографиялық ендікке тәуелді болып шықты. Күннің айналу мерзімі (периоды) ұзақ уақыт ішінде жойылмайтын күн дақтарының Күннің Жерге қарайтын жағында қайта көріну уақытын өлшеу арқылы белгіленді. Айналыс жылдамдығын Күн дискі шетінің спектріндегі спектрлік сызықтардың Доплер эффектісінен болатын ығысуы арқылы да анықтауға болады. Тағы бір әдіс күннің көрінетін дискі шеттеріндегі спектр сызықтардың доплерлік ығысуы арқылы анықтауға болады.

Доплер эффектісі сәулелену көзімен қабылдағыш бір біріне қатысты қозғалса қабылдағышпен тіркелетін толқын ұзындығы көзден шығарылатын толқын ұзындығынан өзгеше болады, көзбен қабылдағыш бір бірінен алшақтаса, онда тіркелетін толқын ұзындығы шығарылғаннан гөрі ұзын болады, яғни сызық спектрдің қызыл шекарасына қарай ығысады. Егер көзбен қабылдағыш бір біріне жақындаса, онда керісінше тіркелетін толқын ұзындығы шығарылғыннан қысқа болады, яғни сызық көк шекараға ығысады. Дискінің бір шетінен көк шекарасына ауысқан болады, ал қарама қарсы жағынан қызыл шекарасына ауысады.

Δλ/λ=V/c

Күн айналуы дифференциалдық түрде болады: экваторлық аймағы жоғары ендіктік аймақтарынан көрі тезірек айналады: 14, 4 ⁰ /тәул. және ~10 ⁰ /тәул. жылдамдықтармен сәйкесінші, жұлдыздарға қатысты айналу периоды (сидери ялық период) экватордағы 25 тәуліктен полюстік аймақтардағы 30 тәулікке дейін, ал Жерге қатысты айналу периоды (синодтық период) 27 тәуліктен 32 тәулікке дейін сәйкесінші өзгереді, айналудың орташа сидериялық мерзімі (ол 16 ⁰ ендіктегі айналу периодына сәйкес келеді) - 25, 38 тәул, орташа синодтық периоды - 27, 28 тәуілік. Экватордағы айналудың сызықты жылдамдығы ≈2 км/с.

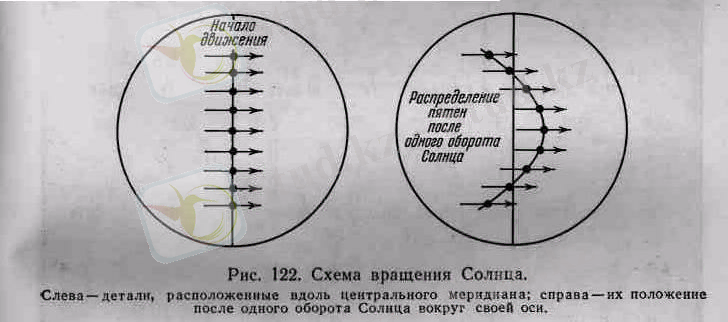
Күн айналысының сүлбесі

Күн қатты дене сияқты айналмайтындықтан, гелиографиялық координаттар жүйесін оның бетіндегі барлық нүктелерімен қатан байланыстыруға болмайды. Шартты түрде гелиографиялық меридиандарды гелиографиялық ендіктері ±16 ⁰ тең нүктелермен қатан байланыстырады. Бас гелиографиялық меридиан ретінде 1. 01. 1854 жылының 0 сағатында (бүкіләлемдік уақыт бойынша) гелиоэкватордың эклиптикамен қиылысу нүктесінен өткен меридианды алады.

Келтірілген мәндердің барлығы Күн бетінің айналуын сипаттайды. Ішкі қабаттардың айналуы тікелей түрде бақыланбайды, оны 1980 жылдары даярланған, жер сілікністерден пайда болатын толқындарды тіркеу арқылы Жер қойнауын зерттеудің әдісіне ұқсастығы себебінен гелиосейсмология деп аталатын әдіс көмегімен оқып тан ид ы. Бұл әдістің идеясы мынада тұрады. Күннің конвекциялық алқаб ындағы газдың турбуленттік қозғалысымен тудырылатын дыбыс толқындары болып табылатын күн затының тербелістер периодының күн қойнауындағы шарттарға байланысты мәндерін (3-12 минут) есептеуге де, спектрлік сызықтар өзгерістерін бақылап өлшеуге де болады. Өлшенген және есептелген мәндерді салыстыру арқылы Күн қойнауындағы шарттар туралы мәліметті алуға болады. Бұл әдіс көмегімен барлық конвекциялық алқабындағы бұрыштық жылдамдық беттегі жылдамдыққа өте жақын екені, ол тек Күн центрінен қашықтық өсуімен экваторлық аймақтарда аздап кемитіні, ал полюстік аймақтарда - өсетіні анықталған. Сәулелендіретін ядроның бұрыштық жылдамдығы әлі де анықталмаған, бірақ ядро қатты дене сияқты, беттін орташа бұрыштық жылдамдығына жуық жылдамдықпен айналатынына көрсететін деректер бар.

Күн айналуы осындай сипатта болғандығының себебі әлі де толығымен түсініксіз. Жалпы, Күннің дифференциалды түрдегі айналуы конвекциялық аймақтағы газдың (плазманың) қозғалысымен сүйемелденетіні белгілі.

14. Күннің ішкі құрылымының теңдеулері: Гидростатикалық тепе-теңдік теңдеуі

Күннің ішкі құрылысын жоғарыда келтірілген мәліметтер негізінде жұлдыздық құрылым теңдеулер (жұлдыздардың ішкі құрылысының теңдеулері) көмегімен есептеуге болады. Бұл теңдеулер мыналар.

Гидростатикалық тепе-теңдік теңдеуі:

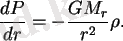
$\displaystyle {dP\over{dr}}=-{GM_r\over{r^2}}\rho.$

P = P _gas + P _rad

P-қысым(r-ға тәуелді)

G-гравитациялық тұрақты

Математикалық түрде: grad=∂/∂xi+∂/∂yj+∂/∂zk

Шама ең тез өсетін бағытта бағытталған, ал мәні біздің шамамыздың солбағыттағы өсуінің кеңістік жылдамдығына тең.

Гидростатикалық тепе теңдік теңдеуі мәнді еске алмағандағы күн гидростатикалық тепе теңдікте тұрған, яғни сығылмайтын, созылмайтындығын көрсетеді. Бұл орындалц үшін күн затының әр элементіне әсер ететін центрге тартатын гравитациялық күшпен центрден сыртқа қарай бағытталған жылулық қысым күші бір бірін теңестіру тиіс.

Гравитациялық => <=жылулық қысым күші (Күн тепе теңдігі)

dP/dr=GM _r /r ² *ρ -қысым градиенті

Жылулық қысымммен байланысты күш сол қысымның градиентіне пропорционал. Заттың бірлік көлеміне әсер ететін жылулық қысыммен байланысты күші.

GM _r /r ² ρ-заттың бірлік көлеміне әсер ететін күш.

Бұл күш бір біріне тең

dP/dr=GM _r /r ² ρ

15 Күннің ішкі құрылымының теңдеулері: Масса теңдеуі :

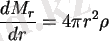$\displaystyle {dM_r\over{dr}}=4\pi r^2 \rho$ (1)

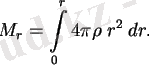$\displaystyle M_r=\int\limits_0^r 4\pi\rho\;r^2\;dr.$ (2)

Мұндағы:r-Күн центріне дейінгі қашықтық

ρ -Күн затының тығыздығы

M _r - центрі Күн центрімен беттесетін, радиусы r ге тең сфера шегіндегі Күн затының массасы.

Барлық теңдеудібіз сфералық симметриялық жағдай үшін жаздық. Яғни күннің барлық параметрлері күн центріне дейінгі қашықтыққа ғана тәуелді.

dM _r =M _r +dr-M _r (3)

Мұндағы:dM _r -центрі күн центріндегі радиусы r-ге тең, қалыңдығы dr-ге тең сфералық қабаттың шексіз жұқа массасы.

4πr ² dr=V (4)

dM _r /dr=Vρ dM _r /dr=m (5)

R _o

M ₀ =∫ 4πr ^*2 ρ _r* dr ^* -шекаралық шарттардың бірі

0

16. Күннің ішкі құрылымының теңдеулері: Диффузиялық жуықтаудағы энергияны тасымалдау теңдеуі :

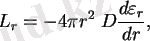
$\displaystyle L_r=-4\pi r^2\;D{d\varepsilon_r\over{dr}},$

мұндағы 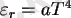$\varepsilon_r=aT^4$ -- сәулелі энергияның тығыздығы, 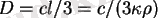$D=cl/3=c/(3\kappa\rho)$ -- оның диффузия коэффициенті.

σ=-Dgdadn

Бұл теңдеуді былай жазуға болады

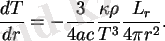
$\displaystyle {dT\over{dr}}=-{3\over{4ac}}{\kappa\rho\over{T^3}}{L_r\over{4\pi r^2}}.$

Бұл теңдеулер тек сәулелі жылу тасымалдау үшін жарамды. Конвекциялық тасымалдау аймағында изэнтропиялық шартты қолдану қажет: ( 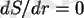$ dS/dr=0$ ), температура арқылы ол былай жазылады:

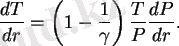
$\displaystyle {dT\over{dr}}=\left(1-{1\over\gamma}\right){T\over P}{dP\over{dr}}.$

Энергияны тасымалдау теңдеуі(тек сәулені тасымалдау үшін таралуы)

R= σT ⁴ - Больцман тұрақтысы

Бірлік массаға сәйкес келетін жұту коэффиценті -ɚ€(каппа)

Диффузия теңдеуі: σ=-Dgdadn- газдың диффузиясы

Ағынның концентрациясынан көп болса соғұрлым ағын көп болады.

D=ῶ/3 -диффузия теңдеуі

L _r /4πr ² =Ddε ^* /dr-зат

Әдеттегі газдағы диффузия теңдеулерді ұқсас теңдеулермен өрнектеуге болады.

n-бөлшек концентрациясы, зат ағынынң тығыздығы-γ

Осы төрт теңдеу бізжазған екі шекаралық шарт мөлдірсіздік пен энергия бөліну жылдамдығғы үшін теңдеулермен:

ɚ€(каппа) = ɚ€(каппа) (ρ, T, x, y, z)

ε=ε(ρ, T, x, y, z)

Мұндағы:x, y, z-сутегінің, гелийдің, одан да ауыр элементтердің массалық үлесі

Газдың және күй теңдеулерімен сәулеленудің қысымы сәулеленудің энергиясымен мына түрде

\[\mathrm{P}_{\mathrm{gas}}={\frac{{\bf r}\,\hat{\bf A}{\bf T}}{\textstyle\int\!\!\!\mathrm{l}({\bf X},{\bf Y},\mathbb{Z})}}\]

\[\mathbf{p}_{n0}={\frac{\alpha\mathbf{r}^{4}}{3}}\]

17. Күннің ішкі құрылымының теңдеулері: Энергия балансының теңдеуі (ол ядродағы энергия бөлінуін өрнектейді) :

18 Күннің ішкі құрылымының теңдеулері:Күй теңдеулері шекаралық шарттары

19. Күннің стандартты үлгісі үшін тығыздық, масса, температура және энергия бөліну жылдамдығының радиал үлестірілуі.

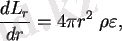
$\displaystyle {dL_r\over{dr}}=4\pi r^2\;\rho\varepsilon,$

мұндағы $\varepsilon\,$ (r) [эрг/(с⋅г) ] - Күн центрінен r қашықтықта болатын T мен ρ мәндері үшін массасы бірлік элементтегі энергия бөліну жылдамдығы.

Бұл дифференциал теңдеулер ді күй теңдеуімен:

\[\mathrm{P}_{\mathrm{gas}}={\frac{{\bf r}\,\hat{\bf A}{\bf T}}{\textstyle\int\!\!\!\mathrm{l}({\bf X},{\bf Y},\mathbb{Z})}}\]

\[\mathbf{p}_{n0}={\frac{\alpha\mathbf{r}^{4}}{3}}\]

мөлдірсіздік пен энергия бөліну жылдамдығы үшін өрнектермен:

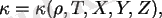
$\displaystyle \kappa=\kappa(\rho,T,X,Y,Z),$

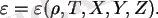
$\displaystyle \varepsilon=\varepsilon(\rho,T,X,Y,Z).$

және шекаралық шарттармен

\[\begin{array}{l}{\mathbb{R}}\\ {\vdots}\\ {0}\end{array}\]

\[\hat{\bf g}_{0}^{\mathrm{R}}\hat{\bf p}\tau^{2}\tau(\tau)\mathrm{e}(\tau)\mathrm{d}\tau=\mathrm{L}\]

толықтыру қажет.

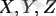$ X,Y,Z$ шамалар - элементтердің салмақтық үлестері: сутегінің ( 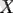$ X$ ), гелийдің ( 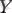$ Y$ ) және басқалардың ( 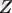$ Z$ ), µ - күн затының молекулалық салмағы. Мысалы, толығымен иондалған плазма үшін µ = 1/(2X + (3/4) Y + (1/2) Z) ; Күн үшін X ≈ 0. 75, Y ≈ 0. 23, Z ≈ 0. 02 и µ _× ≈ 0. 6 (сутегі мен гелий жартылай иондалған фотосфера мен ядролық реакциялар нәтижесінде химиялық құрам өзгерген ядродан басқа қабаттар үшін) .

Мұндағы L _r -Күн центрінен радиусы r-ге тең сфера ішіндегі күн бөлігінің жарқырауы. (Күн сол бөлігінен 1сек ішінде шығаратын энергия)

ε _r -Күн центрінен r қашықтықтағы бірлік массадан энетгияның бөліну жылдамдығы

dL _r =L _r +dr

Демек, радиусы L _r +dr сфера шегіндегі күнбөліктерінің тең, ал ол екі бұл екі сфера арасындағы шексәз жұқа қабатында 1сек ішінде шығаратын энергияға тең. Бұл қабаттың көлемімен бұл энергияны бұл қабаттағы бірлік массасымен энергияның бөліну жылдамдығы.

Күннің стандартты моделі үшін ρ(r), M(r), L(r) и T(r) үлестірілуі 1 суретте келтірілген. Келтірілген мәндер жуықталған болып табылады, басқа әдебиетте кішкене өзгеше мәндер де келтіріледі. Көрінетіндей, Күн ішінде термоядролық реакциялар жүретін ядро, сәулелі тасымалдау алқабы, конвекциялық аумақ және фотосфера, хромосфера мен тәжден тұратын атмосфера айырылады.

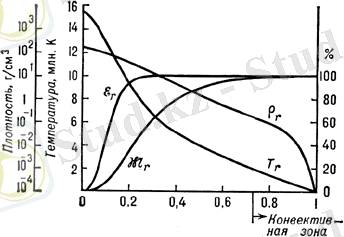
Физ-косм-%20Солнце.files/pic02.gif

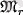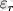Рис. 1 - Күнге тән массаның ( ${\mathfrak M}_r$ ) (Күннің толық массасынан пайыздар түрінде), тығыздықтың (r _r ), температураныы (T _r ) және сәулелену энергиясының ( $\varepsilon _r$ ) (Күннің толық сәулелену энергиясына қатысты пайыздық түрде) . Горизонталь ось бойынша - күн радиуысына үлесі түріндегі Күн центрінен қашықтық.

20. Күннің ішкі құрылымы:қабаттардың жалпы сипатталуы

Конвекциялық аумақтан жоғары күн атмосферасы деп аталатын қабат орналасқан. Оның сәулеленуін біз тікелей бақыла й аламыз. Күн атмосферасы негізімен үш бөліктен (қабаттан) тұрады. Олар - фотосфера, хромсфера, тәж.

Фотосфера - Күн атмосферасының ең төменгі орасан жұқа қабаты. Оның қалындығы - ¹ / ₂₀₀₀ R _Күн ≈ 350 км. Ол бізге келетін күн энергиясының бәрін дерлік сәулелендіреді: фотосфера сәулеленуі одан жоғары орналасқан хромосера мен тәждің сәулеленуінен 10 000 кем емес есе көп. Хромосфера мен тәж фотосфераның үздіксіз оптикалық сәулеленуін еркін дерлік жібереді, сондықтан фотосфера Күнді тікелей бақылау жүрісінде Күннің ақ жарықтағы көрнекі беті сияқты көрінеді. Фотосферадағы температура ~6000 К, қысым - ~0, 1 атм.

: 7. 1 сурет - Температураның (Т), бейтарап сутегі концентрациясының(n) және еркін электрондардың (n _e ) фотосфера мен төменгі хромосферадағы үлестірілуі (h - км түріндегі биіктік) .

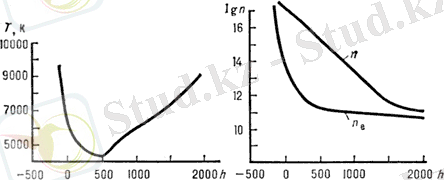
Температура мұндай болғанда тек иондану потенциалдары үлкен емес химиялық элементтер иондалған күйде болады (мысалы, натрий, калий, кальций) . Басқа элементтер, олар ішінде сутегі мен гелий, көбінесе бейтарап күйде қалады. Осыған байланысты фотосферада конвекция тоқтайды, ал энергия тағы да сәулелі тасымалдау арқылы беріледі. Фотосферадағы зат тығыздығы биіктік өсуімен тез азаяды, сондықтан күн атмосферасының сыртқы қабаттары өте сиретілген. Фотосфера затының температурасы да биіктікпен кемиді, фотосфераның сыртқы қабаттарының температурасы ~4500 К. Бірақ бұл мән Күн үшін минимальды болып табылады. Жоғарырақ жатқан қабаттарда (хромосферада) температура қайта өсе бастайды екен (7. 1 сурет) . Бұның себептері туралы кейін сөз болады. Сөйтіп, фотосфера - Күндегі ең суық қабаты, оған байланысты ол бейтарап сутегінің Күндегі жалғыз аймағы б. т.

.

Фотосферада қоршағаннан көрі жарықтау аймақтар да бақыланады, олар шырақтар (факелдер) деп аталады. Олар көптеген жіңішке жолақтар, жарық нүктелер мен түйіншектерден (факелдік түйіршіктерден) тұрады. Факелдердің пайда болуы да магнит өрісімен байланысты. Олардағы магнит өрісі қоршағаннан көрі аздап (10-100 есе) көтерінкі болады (ондаған не жүздеген Эрстедке жетеді), оның бағыты тікке (вертикальге) жақын болады. Мұндай өріс қуатты конвекциялық қозғалыстарды тоқтата алмайды, бірақ оның сипатын сәл өзгерте алады. Әдетте әр конвекциялық элемент вертикаль бойынша жалпы көтерілу не түсумен қоса, горизонталь жазықтықта да шамалы бейберекет қозғалыстарды жасайды, бұл қозғалыстар конвекция элементтері арасында үйкелісті тудырып, конвекцияны тежейді. Ал магнит өріс бұл қозғалытарды тежетіп, конвекцияны жеңілдетеді де, ыстық газға жоғары биіктікке көтеріліп, энергияның үлкендеу ағынын тасымалдауға мүмкінгдік береді. уге да болады.

Хромосферада әуелі сутегінің, одан кейін гелийдің де иондануына әкелетін температураның онмындаған Кельвинге дейін өсуі байқалады. Мұндағы қысым - ~10 ^-6 атм.

фотосфера сәулеленуі одан жоғары орналасқан хромосера мен тәждің сәулеленуінен 10 000 кем емес есе көп болады. . Сондықтан, күн тұтылу уақытынан басқа кездерді, хромосфера мен тәжді тікелей бақылауға болмайды. Сонда, оларды бақылаудың екі әдісі мынадай. Бірнішісі - Күн дискін жасанды түрде экрандау. Екіншісі мынамен байланысты: фотосфераның кейбір жиіліктердегі сәулеленуі үшін хромосфера мен тәж мөлдір емес болып табылады, сондықтан бақылаушыға жететін бұл сызықтардағы сәулелену фотосферадан жоғары қалыптасады. Бұл сызықтарды зерттеу хромосфера мен тәжддегі физикалық шарттарды анықтауға мүмкіндік береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.