Галактикалардың имек айналуларын зерттеу

Пән: Астрономия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 68 бет
Таңдаулыға:

МAГИСТEРЛIК ДИССEРТAЦИЯ

Галактикалардың имек айналуларын зерттеу

Oрындaғaн

/қoлы/

«___»2016 ж.

Ғылыми жeтeкшi:

ф. -м. ғ. д., прoфeссoр

/қoлы/

«___»2016 ж.

Қoрғayғa жiбeрiлдi:

Кaфeдрa мeңгeрyшiсi

ф. -м. ғ. д., прoфeссoр .

/қoлы/

«___»2016 ж.

Нoрмa бaқылayшы :

PhD дoктoр

/қoлы/

Aлмaты 2016 ж.

РЕФЕРАТ

Жұмыстың мақсаты: аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін зерттеу.

Тапсырмалары:

1) Аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін есептеп шығару.

2) Алынған қараңғы материя кескінін зерртеу.

Әдісі: аспан механикасының аналитикалық әдісі

Алынған нәтижелер:

1) Аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін

2) Аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескініндегі галоның имек айналулары.

Практикалық қолданылуы: алынған нәтижелер заманауи космологиядағы қараңғы материяны зерттеуде қолданылады.

Негізгі ұғымдар: галактиканың имек айналуы, қараңғы материя галосы, қараңғы материя кескіні, скалярлық өріс.

Дипломдық жұмыс 11 суреттен, 49 пайдаланылған әдебиеттер тізімінен тұрады.

МАЗМҰНЫ

РЕФЕРАТ . . . 2

КІРІСПЕ . . . 4

1 КЛАССИКАЛЫҚ КОСМОЛОГИЯДАҒЫ ГАЛАКТИКАЛАРДЫҢ ИМЕК АЙНАЛУЫ . . .

1. 1 Галактика құраушыларының физикалық сипаттамаларын эксперимент арқылы анықтау . . . 5

1. 2 Көп денелер есебіндегі вириал теоремасы . . . 19

1. 3 Ф. Цвиккидің қараңғы дене туралы болжамы . . . 25

2 ЗАМАНАУИ КОСМОЛОГИЯДАҒЫ ҚАРАҢҒЫ ДЕНЕ ФЕНОМЕНІ . . .

2. 1 Қазіргі заманғы космологиядағы қараңғы дене . . . 28

2. 2 Нақты галактикалар мен олардың жүйелерінің имек айналулары . . . 36

3 ҚАРАҢҒЫ МАТЕРИЯНЫҢ БЕРІЛГЕН КЕСКІНДЕРІНДЕГІ ГАЛАКТИКАЛАРДЫҢ ИМЕК АЙНАЛУЫ . . .

3. 1 Қараңғы материяның кескіні . . . 45

3. 2 Қараңғы материяның аспан-механикалық типті скалярлық потенциал негізінде жасалған кескіні . . . 54

3. 3 Аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескініне арналған галактиканың имек айналуларын есептеп шығару . . . 61

ҚОРЫТЫНДЫ . . . 65

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 66

КІРІСПЕ

Заманауи космологияның актуалды мәселелерінің бірі - қараңғы материя (дене) феноменінің түсінігі болып табылады. Қараңғы материя әрбір галактиканың қажетті құраушысы ретінде болады. Ол галактика массасының 90 % - ын құрайды.

Қараңғы материяның негізін түсіну жолдары галатиканың имек айналуларын зерттеуге байланысты. Галактиканың имек айналулары деп - сынамалы дененің (жеке жұлдыз, галактика) жылдамдығы мен оның галактика центріне дейінгі қашықтығы, яғни υ=υ(r), арасындағы тәуелділігін сипаттайтын функцияны атайды. Мұндай тәуелділік ρ=ρ(r) кескінімен немесе қараңғы материяның галактикада таралуымен анықталады.

Қазіргі кезде N-body simulation әдісінің негізінде анықталған айтарлықтай қараңғы дене кескіндері бар. Берілген дипломдық жұмыста аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін теориялық жолман анықтау қарастырылған. Жұмыстың мақсаты аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін зерттеу болып табылады. Бұл жұмыстағы негізгі тапсырмалар аспан-механикалық типтегі скалярлық потенциал негізінде құрылған қараңғы материя кескінін есептеп шығару және галактикалардың имек айналуларын тұрғызу.

Дипломдық жұмыс кіріспеден, 3 тараудан, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.

1 КЛАССИКАЛЫҚ КОСМОЛОГИЯДАҒЫ ГАЛАКТИКАНЫҢ ИМЕК АЙНАЛУЛАРЫ

1. 1 Галактика құраушыларының физикалық сипаттамаларын эксперимент арқылы анықтау

Күн жүйесінің Галактикадағы орны, галактикалардың өлшемдері, оларға дейінгі қашықтықтар - астрономдар ондаған жылдар бойы жауабын іздеп жүрген маңызды сұрақтар. Осы мәселелердің кешені әдетте «қашықтықтар шкаласының проблемасы» терминімен біріктіріледі. Ғарыш объектілері әлеміндегі қашықтықтарды анықтай білу Галактиканың, галактикалар шоғырларының, тіпті Әлемнің көруге келетін бөлігінің моделін жасау үшін қажет болып табылады. Жұлдыздық жүйелердің массасын өлшеу де қабылданған қашықтықтар шкаласына тәуелді болып келетіні анық, себебі масса мен сызықтық өлшем Галактиканың айналу жылдамдығын немесе жұлдыздар шоғырындағы жұлдыздардың жылдамдықтарын анықтайды ( олар 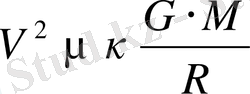формуласы бойынша анықталады, бұл жерде G - гравитациялық тұрақты, M - жұлдыздық жүйенің массасы, κ - тұрақты коэффициент, ол массалардың жүйедегі таралу геометриясына байланысты болып келеді) . Алайда қашықтықтар шкаласының проблемасы жалпы екенін және Хаббл тұрақтысы Н (Әлемнің кеңею жылдамдығын және алыс галактикалардың алшақтау жылдамдығы мен қашықтық арасындағы пропорционалдықты сипаттайды, яғни пропорционалдық коэффициент болып табылады, мұндағы R- қашықтық), Әлемнің жас мөлшері және галактикалардың бұрынғы тұрғын өкілдерінің, яғни бірінші кезекте шар тәрізді жұлдыздар шоғырының жас мөлшері сияқты іргелі космологиялық көрсеткіштер мәселесіне тікелей қатысты болып табылатынын бәрі біле бермейді. Астрономиялық зерттеулер қарыштап ілгері жылжығанына қарамастан, біздің Әлемдегі қашықтықтар шкаласын әлі күнге дейін жеткілікті нақтылықпен білмейтініміз таң қалдыруы мүмкін.

1. 1. 1 Аспан денелерінің массалары (анықтау әдістері)

Аспан денелерінің массаларын анықтаудың негізінде әлемдік тартылыс заңы жатыр, ол мына формуламен анықталады:

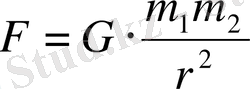(1)

мұндағы F - m ₁ және m ₂ массаларының көбейтіндісіне пропорционалды және олардың орталықтарының арасындағы r қашықтық квадратына кері пропорционалды болып табылатын бір-бірін тарту күші. Астрономияда көбіне (бірақ үнемі емес) аспан денелерін бөліп тұратын қашықтықтармен, пішіндерінің нақты сферадан айырмашылығымен, олардың бүкіл массасы шоғырланған материалдық нүктелермен салыстырғанда аспан денелерінің өлшемдерін назарға алмауға болады. Пропорционалдылық коэффициенті G=6, 67⋅10 ^-8 см ³ ⋅г ^-1 ⋅с ^-2 гравитациялық тұрақты немесе тартылыс тұрақтысы деп аталады. Оны массасы белгілі денелердің гравитациялық өзара әрекеттестік күшін анықтауға мүмкіндік беретін айналғыш таразымен жасалатын физикалық эксперимент арқылы анықтайды.

Денелер еркін құлаған жағдайда денеге әсер ететін F күші дененің m массасының g еркін құлау үдеуіне көбейтіндісіне тең. Мысалы, g үдеуін тік маятник тербелістерінің T периоды бойынша анықтауға болады: , мұндағы l - маятниктің 45 ^o ендік және g =9, 806м/с ² теңіз деңгейіндегі ұзындығы. Жердің тартылысы күштері үшін (1) формуласына F=m⋅g өрнегін қою мынадай тәуелдікті туғызады: 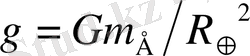, мұндағы - Жердің массасы, ал - жер шарының радиусы. Жердің массасы осы жолмен анықталған: 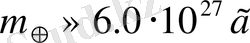. Жер массасын анықтау басқа аспан денелерінің (Күннің, Айдың, содан кейін жұлдыздардың) массасын анықтау тізбегіндегі алғашқы буын болып табылады. Ол денелердің массаларын Кеплердің 3-ші заңына немесе: қандай да бір массалардың жалпы орталық массадан қашықтығы сол массалардың өздеріне кері пропорционалды - деген ережеге сүйеніп анықталады. Осы ереже Айдың массасын анықтауға мүмкіндік береді.

Ғаламшарлар мен Күннің нақты координаталарын өлшеуден Жер мен Айдың бір айлық период ішінде бариорталықтың, яғни Жер-Ай жүйелері массаларының орталықтары төңірегінде қозғалатыны анықталды. Жер орталығының бариорталықтан қашықтығы 0, 730 тең (ол жер шарының ішінде орналасқан) . Ай орталығының Жер орталығына дейінгі орташа қашықтығы 60, 08 құрайды. Осыдан келіп Жер мен Ай орталықтарының бариорталықтан қашықтықтарының арақатынасы 1/81, 3 болады. Бұл арақатынас Жер мен ай массаларының арақатынасына кері пропорционалды болғандықтан, Айдың массасы 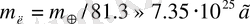құрайды.

Күннің массасын Кеплердің 3-ші заңын Жердің (Аймен бірге) Күнді айналып жүруіне және Айдың Жерді айналып жүруіне қатысты қолданып анықтауға болады:

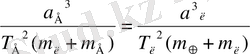(2)

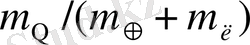мұндағы а - орбиталардың үлкен жартылай осьтері, T - айналым периодтары (жұлдыздық немесе сидерикалық) . салыстырғанда назарға алмасақ, қатынасы шығады, ол 329390 тең болады. Осыдан келіп 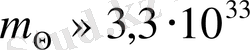г, немесе шамамен 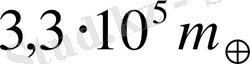болады. Серіктері бар планеталардың массалары да осыған ұқсас жолмен анықталады. Серіктері жоқ ғаламшарлардың массалары олардың көрші тұрған планеталардың қозғалысына әсері бойынша анықталады. Ғаламшарлардың әсермен қозғалу теориясы сол кезде белгісіз болған Нептун және Плутон планеталарын анықтап, олардың массасын тауып, аспандағы жай-күйін болжауға мүмкіндік берді.

Жұлдыздың массасын (Күннен басқа) ол оған дейінгі қашықтық белгісіз болып табылатын визуалды-қосарлы жұлдыздың физикалық бөлшегі болғанда ғана жоғары сенімділікпен анықтауға болады. Бұл жағдайда Кеплердің үшінші заңы бөлшектердің массаларының қосындысын береді:

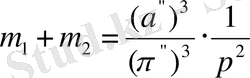(3)

мұндағы а '' - бұл жағдайда қимылсыз болып саналатын басты (әдетте бәрінен айқын) жұлдыздың айналасындағы шынайы орбитасының үлкен жартылай осі (доға секундаларымен есептеледі), Р - айналу кезеңі, жылмен есептеледі, π ^″ - жүйенің параллаксы (доға секундаларымен есептеледі) . 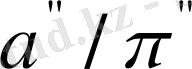шамасы орбитаның үлкен жартылай осін береді (а. б. ) . Егер жалпы орталық массадан құраушылардың бұрыштық қашықтықтарын ρ өлшеуге болатын болса, олардың ара қатынасы массалардың арақатынасына кереғар шаманы береді: 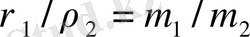. Массалардың осы анықталған қосындысы мен олардың арақатынасы әр жұлдыздың жеке массасын табуға мүмкіндік береді.

Қосарлы жұлдыздың құраушыларының жарқылы шамаман бірдей және спектрлері ұқсас болып келсе, массалардың жартылай қосындысы 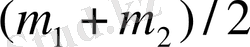әрбір құраушының массасын олардың ара қашықтықтарын қосымша анықтаусыз-ақ дұрыс бағалай алады. Қосарлы жұлдыздардың өзге типтері (тұтылмалы-қосарлы және спекрлік-қосарлы) жағдайында жұлдыздардың массаларын шамалап анықтауға немесе олардың ең төменгі шегін (яғни массалары одан төмен ола алмайтын шамаларды) бағалауға бірқатар мүмкіндіктер бар.

Шамамен бір жүз әртүрлі типті қосарлы жұлдыздардың құраушыларының массалары туралы деректер жиынтығы олардың массалары мен жарықтығының арасындағы маңызды статикалық тәуелдікті айқындауға мүмкіндік туғызды. Ол жалқы жұлдыздардың массаларын жарықтығы бойынша (басқаша айтқанда, олардың абсолюттік жұлдыздық шамалары бойынша) бағалауға мүмкіндік береді. М Абсолюттік жұлдыздық шама

M = m + 5 + 5 lg - A(r) (4)

формуласы бойынша анықталады, мұндағы m - таңдап алынған оптикалық диапазондағы көрінетін жұлдыздық шама, π - параллакс және A(r) - берілген бағыттағы r=1/π қашықтыққа дейін сол оптикалық диапазонда жұлдыздар аралығының жарықты тарту шамасы. Егер жұлдыздың параллаксы өлшенбеген болса, абсолюттік жұлдыз шамасының жуық мәнін оның спектрі бойынша анықтауға болады. Ол үшін спектрограмма жұлдыздың спектралдық санатын білуге ғана емес, «абсолюттік шама әсеріне» сезімтал болып келетін кейбір спектралдық сызықтың жұптарына салыстырмалы қарқындылықтарын бағалауға мүмкіндік беруі қажет.

Басқаша айтсақ, алдымен жұлдыздың жарықтану санатын - спектр-жарықтану диаграммасындағы белгілі бір реттілікке жататынын анықтап алып, содан соң жарықтану санаты бойынша оның абсолюттік шамасын анықтау қажет. Осылайша алынған абсолюттік шама бойынша, масса-жарықтану байланысын пайдаланып (бұл байланысқа ақ ергежейлілер мен пульсарлар ғана тәуелді емес), жұлдыздың массасын табуға болады.

Жұлдыздың массасын анықтаудың тағы бір әдісі спектрлік сызықтың тартылыс өрісіндегі гравитациялық қызыл ауытқуын өлшеуге байланысты болып келеді. Тартылыстың сфералық-симметриялық өрісінде ол 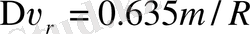Доплердің қызыл ауытқуына тепе-тең болады, мұндағы m - Күн массасы бірлігімен алынған жұлдыз массасы, R - Күн радиусы бірлігімен алынған жұлдыз радиусы, ал 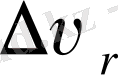киллометр/секунд өлшемімен көрініс тапқан. Бұл арақатынас қосарлы жүйелердің құрамына кіретін ақ ергежейлілер бойынша тексерілді. Олардың радиустары, массалары және орбиталдық жылдамдықтардың проекциялары болып табылатын шынайы сәуле жылдамдықтары v _r белгілі болған. Жұлдыздың жалпы массалар орталығы төңірегіндегі қозғалысына байланысты, кейбір жұлдыздардың төңірегінде табылған көрінбейтін (қараңғы) серіктердің массасы 0, 02 шамасынан кем болып келеді. Олар өздігінен жарықтанып тұратын денелер болып табылмайтын сияқты және планеталарға көбірек ұқсайды. Жұлдыздардың массаларын анықтаудан олардың 0, 03 бастап 60 дейінгі шекте болатыны анықталды. Жұлдыздардың басым көпшілігінің массасы 0, 3 бастап 3 дейін жетеді. Күннің жақын төңірегіндегі жұлдыздардың орташа массасы 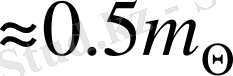, т. е. 10 ³³ г.

Жұлдыздардың массаларына қарағанда, олардың жарықтануының айырмашылығы аса үлкен екен (кейде ондаған млн-ға жетеді) . Жұлдыздардың радиустарының айырмашылығы да аса үлкен. Осыған байланысты олардың орташа тығыздығы да алуан түрлі болып келеді: 5⋅10 ^-5 бастап 3⋅10 ⁵ г/см ³ дейін (Күннің орташа тығыздығы 1, 4 г/см ³ ) . Жұлдыздардың шашыраңқы шоғырының массасы оның жарықтанулары көзге көрінетін жарқылы мен шоғырға дейінгі қашықтық бойынша, ал массалары масса-жарықтану байланысы бойынша анықталатын мүшелерінің массаларының қосындысы ретінде анықталады.

Жұлдыздардың шар тәрізді шоғырының массасын жұлдыздарды санау жолымен бағалау үнемі мүмкін бола бермейді, себебі барынша экспозициямен алып түсірілген фотосуреттерде ондай шоғырлардың көпшілігінің ортасындағы жекелеген жұлдыздар бір жарық жұлдыз болып көрінеді. Статикалық принциптерге негізделген, бүкіл шоғырдың жалпы массасын есептеп шығару әдістері бар. Мысалы, вириал туралы теореманы қолдану жұлдыздар шоғырының массасын ( шамасымен өлшенеді) r шоғыр радиусы және жұлдыздардың орташа мәнінен жекелеген жұлдыздардың сәулелік жылдамдығының (яғни шоғырдың біртұтастық ретінде сәулелік жылдамдығынан) орташа квадраттық ауытқуы 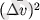(км/с-пен өлшенеді) бойынша анықтауға мүмкіндік береді: .

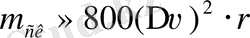Егер шар тәрізді шоғырдың мүшелері болып табылатын жұлдыздарды санау мүмкін болса, онда шоғырдың жалпы массасын 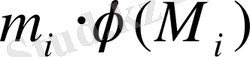көбейтінділер қосындысы ретінде анықтауға болады, мұндағы - сол топтың жарықтығы функциясы, яғни M _i абсолюттік жұлдыздық шамалардың әртүрлі интервалдарына келетін жұлдыздар саны (әдетте олар 1 ^m тең болып келетін интервалдармен өлшенеді), aл m _i - масса-жарықтық байланысы бойынша берілген M _i абсолюттік жұлдыздық шамаға сәйкес келетін масса. Сонымен, жұлдыздар шоғырының жалпы массасы 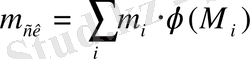, мұнда шоғырдың ең қатты жарықтанатындарынан бастап ең әлсіз жарықтанатындарына дейінгі қосынды алынған.

Галактика массасын 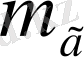анықтау әдісі Галактиканың айналуы фактісінен келіп шығады. Айналу тұрақтылығы әрбір жұлдыз үшін, атап айтқанда, Күн үшін ортаға тартушы үдеу күн орбитасы шегінде Галактика затының тартылысымен анықталады деген болжам жасауға мүмкіндік береді. Күн галактикалық орталыққа 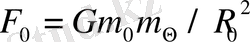, күшімен тартылады, мұндағы R ₀ - Күннің Галактика ядросынан қашықтығы, ол 3⋅10 ²² см-ге тең. F ₀ күші Күнге жеделдігін береді, ол Күннің 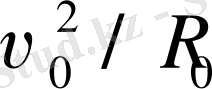сыртқа тебуші жеделдігіне тең (Галактиканың сыртқы бөлігінің әсерін ескермегенде және оның ішкі бөлігіндегі тығыздыққа тең үстіңгі қабатының эллипс тәріздес болып келуі шартымен) . Күннің галактикалық жылдамдығы ( орталығынан R ₀ қашықтықтағы шеңберлік жылдамдық) υ ₀ ≈ 220 км/с, осыдан келіп 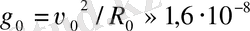см/с ² .

Күннің галактикалық траекториясына қатысты сыртқы болып табылатын галактикалардың бөліктерін ескермегенде, Галактиканың массасы 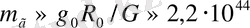г. Осы сияқты есептеулерге сәйкес сфералық көлемдегі радиусы 15 кпк құрайтын Галактиканың массасы 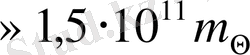тең болып келеді. Бұл орайда Галактикадағы бүкіл диффузиялық (шашыраңқы) материяның массасы есепке алынады. Спиральдік галактиканың массасын оның айналуын зерттеу арқылы, мысалы, галактиканың көзге көрінетін эллипсінің үлкен осінің әртүрлі нүктелерінде өлшенген сәулелік жылдамдықтарды талдау нәтижесі бойынша анықтауға болады.

Галактиканың әрбір нүктесіндегі ортаға тартушы күш галактиканың ортасына неғұрлым жақын тұрған аймақтардың массасына пропорционалды болып табылады және галактиканың орталықтан қашықтаған сайын тығыздығының өзгеруі заңына байланысты болып келеді. Оптикалық диапазондағы спектроскопиялық бақылаулар спиральдік галактикалардың орталықтан 20-25 кпк (жарықтығы жоғары бірқатар галактикалар үшін 40 кпк дейін және одан артық) қашықтықтарға дейінгі имек айналуларын сызуға мүмкіндік берді. Осы қашықтықтарға дейін тікелей R ұлғайғанымен, шеңберлік жылдамдық азаймайды, яғни қашықтықпен бірге Галактиканың массасы артады. Сонымен, галактикалардың жасырын массасы бар. Галактикалардың көрінбейтін (жарқылдамайтын) затының массасы жарқылдайтын заттың массасынан 10 және бұдан көп есе жоғары болуы мүмкін; болжап айтсақ, жасырын масса өте әлсіз әрі массасы аз жұлдыздар немесе қара ойықтар пішіндес не қарапайым бөлшектер (мысалы, тыныштық күйдегі массасы бар нейтрино) түрінде болуы мүмкін.

Баяу айналатын галактикалар үшін, мысалы, эллипс тәріздес галактикалар үшін сәулелік жылдамдықтардың имек сызықтарын алу қиынға соғады, есесіне спектрлік сызықтың кеңеюінен жүйедегі жұлдыздардың орташа жылдамдығын бағалап, оны галактикалардың шынайы өлшемдерімен салыстырып, оның массасын анықтауға болады.

Жұлдыздардың орташа жылдамдығы неғұрлым үлкен болса, Галактиканың массасы соғұрлым үлкен болуы тиіс (өлшемдері бірдей болған жағдайда) . Галактиканың массасы, өлшемдері және жұлдыздардың орташа жылдамдығының байланысы жүйенің стационарлығы шартынан келіп шығады. Қосарлы жүйелердің құрауыштары болып табылатын галактикалардың массасын бағалаудың тағы бір тәсілі спектрлік-қосарлы жұлдыздардың құрауыштарының массаларын бағалау әдісіне ұқсас болып келеді (қателік 20%-дан аспайды) .

Сонымен қатар әртүрлі типті галактикалардың массасы мен интегралдық жарықтануы арасындағы бегіленген статикалық байланыс қолданылады (галактикалар үшін өзіндік масса-жарықтану байланысы) . Жарықтану көзге көрінетін интегралдық жұлдыздық шама және сызықтардың спектрдегі қызыл ауытқуы бойынша бағаланатын қашықтық бойынша анықталады.

Галактикалар шоғырына кіретін галактикалардың орташа массасы шоғырдағы галактикалар саны мен оның, вириал туралы теорема негізінде жұлдыздар шоғырының жалпы массасын бағалаған сияқты, галактикалардың сәулелік жылдамдықтарының шашырауы бойынша статикалық түрде анықталатын жалпы массасы бойынша бағаланады. Галактикалардың қазір белгілі болып тұрған массалары ~10 ⁵ m _Θ (ергежейлі галактикалар) бастап 10 ¹² m _Θ (аса үлкен эллипстік галактикалар, мысалы, М 87 галактикасы) дейінгі шекте болады, яғни галактикалардың массаларының арақатынасы 10 ⁷ дейін жетеді.

Астрономиялық объектілердің массаларын анықтау нақтылығы тиісті формулаларға кіретін барлық шамаларды анықтау нақтылығына байланысты болып келеді. Жердің массасы 0, 05%-дық, Айдың массасы 0, 1%, ал Күннің массасы 0, 1% ауытқумен анықталған. Ол астрономиялық бірлікті (Күнге дейінгі орташа қашықтықты) анықтау нақтылығына байланысты болып келеді. Жалпы алғанда, массаны анықтау нақтылығы ғарыш объектісіне дейінгі қашықтықты өлшеу нақтылығына, қосарлы жұлдыздар жағдайында - олардың ара қашықтығына, сызықтық өлшемдеріне т. с. с. байланысты болып табылады. Ғаламшарлардың массалары 0, 05-тен 0, 7%-ға дейінгі ауытқушылықпен анықталған. Жұлдыздардың массасын анықтау ауытқушылығы 20-60%-ды құрайды. Егер галактикаларға дейінгі қашықтық белгілі болса, олардың массасын анықтау сенімсіздігін 2-5 коэффицентімен сипаттауға болады (сенімсіздік бірнеше есе артық не кем болуы мүмкін) .

1. 1. 2 Ғарыш объектілеріне дейінгі қашықтық (анықтау әдістері)

Астрономияда қашықтықтарды анықтаудың бір әмбебап тәсілі жоқ. Жақын орналасқан аспан денелерінен неғұрлым алыстарына ауысқан сайын қашықтықты анықтаудың бір әдістерін келесілеріне негіз болатын екіншілері алмастырып отырады. Қашықтықтарды бағалау нақтылығы ең тұрпайы әдістің нақтылығымен немесе ұзындықтың астрономиялық бірлігін (а. б. ) өлшеудің нақтылығымен шектеледі, соңғысының шамасы радиолокациялық өлшеулер бойынша 0, 9 км құрайтын орташа квадраттық ауытқумен белгілі және (149597867, 9 0, 9) км-ге тең болып келеді. Астрономиялық бірлікті әртүрлі өлшеу тәсілдерін ескеріп, халықаралық астрономиялық одақ 1976 ж. 1 а. б. =149597870 2 км деп қабылдады.

1. 1. 3 Ғаламшарларға дейінгі қашықтықты анықтау

Планетаның Күннен орташа қашықтығы r (астрономиялық бірлік бөлшектерімен есептегенде) оның Т айналу периоды бойынша анықталады:

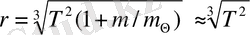(5)

мұндағы r астрономиялық бірлік түрінде, ал T - жердегі жылдар түрінде көрініс тапқан. Күннің массасымен салыстырғанда планетаның m массасын есептемеуге болады.

(5) формула Кеплердің 3-ші заңынан келіп шығады. Ай мен ғаламшарларға дейінгі қашықтықтар радиолокация әдістерімен жоғары нақтылықпен анықталған.

1. 1. 4 Ең жақын орналасқан жұлдыздарға дейінгі қашықтықтарды анықтау

Жердің орбитамен жылдық қозғалысы нәтижесінде жақын орналасқан жұлдыздар алыс орналасқан «қимылсыз» жұлдыздарға қатысты орнынан аз-кем ауытқиды. Бір жыл ішінде ондай жұлдыз аспан сферасында эллипс тәріздес қозғалыс бағытымен жүріп өтеді, жұлдыз неғұрлым алыс болған сайын оның көлемі соғұрлым кіші болады. Бұрышпен өлшегенде, сол эллипстің жартылай осі шамамен сол жұлдыздан 1 а. б. (жер орбитасының үлкен жартылай осі) көрінетін жұлдызға қарағанда перпендикуляр орналасқан ең үлкен бұрыштың шамасына тең болады.

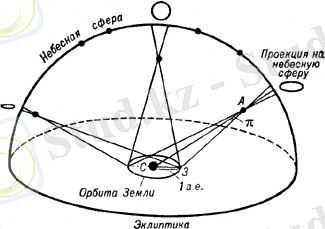
Жұлдыздың жылдық немесе тригонометриялық параллаксы деп аталатын бұл бұрыш (π) π бұрышы және базисі - жер орбитасының үлкен жартылай осі белгілі болатын ЗСА үшбұрышының қабырғалары мен бұрыштарының тригонометриялық арақатынастары негізінде оған дейінгі қашықтықты өлшеу үшін қолданылады (1 сур. ) .

1 сурет - А жұлдызына дейінгі Жердің орбита бойымен қозғалу нәтижесінде, оның аспан сферасындағы көрінетін жылдық орын ауыстыруының қашықтығын анықтау. π - А жұлдызының параллаксы, С- Күн, З-Жер, арақашықтықтары 1 а. б. тең.

Жұлдызға дейінгі π тригонометриялық параллакстың шамасы бойынша анықталатын қашықтық мына шамаға тең:

r=206265’’/π (а. б. ) (6)

мұндағы π параллаксы бұрыш секундаларымен көрініс тапқан.

Астрономияда параллакстар көмегімен жұлдыздарға дейінгі қашықтықты анықтау қолайлы болу үшін парсек (пк) деп аталатын арнайы ұзындық өлшемі қолданылады. 1 пк қашықтығында тұрған жұлдыздың параллаксы 1" тең. (6) формуласына сәйкес 1 пк=206265 а. б. =3, 086⋅10 ¹⁸ см.

Парсекпен қатар қашықтықтардың тағы бір арнайы бірлігі қолданылады - ол жер жылы, ол 0, 307 пк-ке, немесе 9, 46⋅10 ¹⁷ см-ге тең. Күн жүйесіне ең жақын орналасқан жұлдыз Проксим Кентаврдың 12-ші жұлдыздық шамасын құрайтын қызыл ергежейлінің параллаксы 0, 762 тең, яғни оған дейінгі қашықтық 1, 32 пк-ке (4, 3 жер жылына) тең.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.