Сигналдардың Фурье-талдауы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

СИГНАЛДАРДЫҢ ФУРЬЕ-ТАЛДАУЫ

Фурье-талдаудың идеясы

Сигналардың Фурье-талдауы кезкелген дерлік функцияны тригонометриялық қатарға жіктеуге болады деген идеяда негізделген. 1823 ж. француз математигі Фурье мұндай жіктеудің коэффициенттері үшін өрнектерді ұсынды. Бірақ сол кезде бұл болжауға сенген ірі математиктер аз болды, өйткені Фурье сендіретін дәлелдеуді келтіре алмады, ал дәлелсіз мұндай жорамалға сенуге қиын. Синусоидалар сияқты қарапайым функцияларды қосу нәтижесінде оларға тіпті ұқсамайтын және пішіні өте күрделі функцияларды алуға болатыны мүмкін емес болып көрінеді.

Бұл болжау рас болып шыққанын сендер білесіндер, оның мүлтіксіз дәлелдеуін 1829 ж. Дирихле келтіріді. 1 суретте мысал үшін амплитуда мен жиіліктері әртүрлі бірнеше синусоидаларды қосындылау нәтижесінде тікбұрышты импульстері тізбегі болып табылатын сигналды жуықтап алуға болатындығы көрсетілген (былайша айтсақ, бұл сигналдың Фурье қатарының дербес қосындылары (бұл сигналдың Фурье қатарын қосындылаудың аралық кезендері) көрсетілген) . Төрт-ақ синусоиданы қосқанда бұл сигналға өте ұқсас функция алынатыны, қосылатын синусоидалардың (Фурье қатары мүшелерінің) саны өскен сайын керекті сигналды жуықтау дәлдігі өсетіні жақсы көрінеді. Бірақ сигналдың үзіліс нүктелері маңайындағы тербелістердің ( алынбақ отырған сигналдан ауытқұлардың) амплитудалары қосылып отырған синусоидалардың саны өсуімен азаймайтыны дерлік, тек горизонталь бойынша сығылып, үзіліс нүктелеріне жақындайтыны да көрінеді. Бұл құбылыс Гиббс эффекті деп аталады, ол Фурье- талдау кемшіліктерінің бірі болып табылады.

1 сурет - Қосылатын ең жоғарғы гармониканың нөмірі k=1, 3, 5, 7, 9, 11, 13, 15 болғандағы меандр үшін Фурье-синтезінің аралық кезеңдері -

Бірақ-та, Фурье қатарына жіктеуде негізделген сигналдарды талдаудың әдісі қазіргі уақытта да, вейвлеттік, информациялы-энтропиялық, т. с. с. талдаудың жетілдірілген әдістері ашылған болса да, өз маңыздылығын сақтады. Өйткені сигналды оның элементар құраушыларына жіктеп, ол туралы көптеген мәліметті, мысалы, оның шыққан тегісі туралы, оның көзі болып табылатын объекттің ерекшеліктері туралы, көзден қабылдағышқа дейінгі жолда оған әсер еткен факторлар, яғни ол таралған ортаның қасиеттері туралы, т. с. с. мәліметті алуға болады. Бұл, мысалы, жұлдыздар шығаратын жарықтың спекрін талдап, яғни жарықты жиіліктік құраушыларына жіктеп, жұлдыз затының құрамын, температурасын, жұлдызаралық ортаның қасиеттерін анықтағанға ұқсас. Мұның үстіне, физикалық әлемде жиіліктері әртүрлі тербелістердің қосындысы болып табылатын құбылыстар көп екен (мысалы, жарық) . Жалпы, Фурье қатарларын көптеген уақыт ішінде есептеу мен талдауды жүргізу үшін өте ыңғайлы математикалық абстракция деп ойлады, бірақ радиобайланыстың пайда болуымен күрделі сигналдардың гармоникалары (гармоникалық құраушылары) шынында да бар объектілер болып табылатыны, және әр сигнал олардың жыйынтығымен (спектрімен) сипатталынатыны ашылды. Күрделі сигналдардың синтезаторлары мен спектрдің анализаторларын жасау Фурье-талдаудың триумфі болды.

Фурье болжаудың дәлелдеуі элементар тригономтериялық түрленулер мен Фурье қатарын құрайтын функциялардың ортогогональдығында негізделген, ол математикалық талдау курсында беріледі. Мұнда функцияны Фурье-қатарға жіктеудің геометриялық аналогиясын, яғни әдеттегі векторды үшөлшемді кеңістікте үш ортогональ векторлар (кеңістіктің базисі) бойынша жіктеуге ұқсастығын қарастыруға пайдалы болады, өйткені осы принципте сигналдарды талдаудың басқа да әдістері, мысалы, вейвлет-талдауы, негізделген .

Үшөлшемді кеңістіктегі кезкелген векторды нүкте арқылы анықтауға (вектордың басы координаттар жүйесінің басымен сәйкестірілгендегі вектордың ұшына (соңына) сәйкес келетін нүкте ретінде көрсетуге) болады және базистік векторлар бойынша, мысалы, декарт координат жүйесі остерінің орттарынан құрастырылған { i, j, k } ортонормаланған базисі бойынша, жіктеуге болады (олардың сызықты комбинациясы түрінде :

a =a _x i + a _y j + a _z k .

Мұндағы a _x , a _y және a _z жіктеу коэффициенттері вектордың құраушылары (компоненттері, i, j, k бағыттардағы проекциялары) деп аталады да, жіктеліп отырған вектор мен сәйкесті базистік ветордың скалярлық көбейтіндісімен анықталады: a _x = (a i), …

Жалпы жағдайда, базистік веторлар бірлік болмағанда, бұл формулаларды былай жазуға болады:

a =a ₁ e ₁ + a ₂ e ₂ + a ₃ e _3, 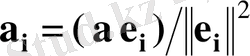, мұндағы - e _i векторының нормасы, яғни вектордың өз өзіне скалярлық көбейтіндісінің түбірі (вектордың модулі (ұзындығы) ) : .

Кеңістіктің көптеген базистер, яғни оларға кезкелген векторды жіктеуге болатын векторлар жиынтығы, болуы мүмкін (мысалы, сәйкес остері бір бірімен беттеспейтін (бір біріне бұрыштар жасап бағытталған) декарт координат жүйесі остерінің орттарынан құрастырылған базистердің шексіз саны бар, полярлық координаттар жүйесінің базисі, т. б. ), бірақ әр базисті құрайтын векторлардың саны барлық базистер үшін бірдей, кеңістіктің өлшемділігіне тең болады.

Сигналдар теориясында кезкелген функция (сигнал) функциялардың кеңістігі деп аталатын абстрактты көпөлшемді кеңістіктегі көпөлшемді вектор ретінде қарастырылады, оған бұл кеңістіктегі бір нүкте сәйкес келеді, функцияның әр мәні вектордың бір құраушысын (векторға сәйкес келетін нүктенің бір координатасын) береді (анықтайды) . Егер сигнал үздіксіз болса, онда оның мәндерінің саны ақырсыз болады, демек ол шексізөлшемді кеңістітегі шексізөлшемді вектор болып табылады. Егер сигнал дискретті болып табылса, және оның санақтарының саны N болса, ол N-өлшемді кеңістіктегі N-өлшемді вектор болып табылады.

Екі үздіксіз сигналдың [a, b] аралығындағы скалярылық көбейтіндісі былай анықталады:

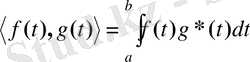Бұл анықтама әдеттегі үшөлшемді векторлардың скалярлық көбейтіндісіне ұқсас енгізілген: ол екі вектордың сәйкес құраушылар көбейтінділерінің қосындысына тең болады (( ab ) = a ₁ b ₁ + a ₂ b ₂ + a ₃ b ₃ ), үздіксіз сигналдар үшін қосудың орнына интегралдау жасалынады, функциялар копмлексті болып табылса, екінші функцияның орнына оның түйіндес функциясы алынады. Кейде скалярылық көбейтіндісін [a, b] аралығына нормалайды (бұл аралық бойынша орташалайды) :

Сәйкесінше, функцияның нормасы былай анықталады:

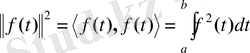, немесе .

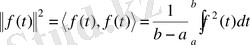Сонда, егер {ϕ ₁ , ϕ ₂ , … } функциялардың тізбегі (жүйесі) кеңістігінің базисі болып табылса, яғни бұл кеңістікке жататың кезкелген функцияны ϕ ₁ , ϕ ₂ , … функцияларының сызықты комбинациясы ретінде көрсетуге болса, онда Сонда біздің функциялық кеңістікке жататың кезкелген f “векторды” (функцияны) жалғыз түрде {ϕ ₁ , ϕ ₂ , … } толық ортогональ жүйенің “векторлары” бойынша (яғни бұл кеңістіктің базисі болып табылатын {ϕ ₁ , ϕ ₂ , … } ф ункциялар тізбегі не (жүйесіне) кіретін функциялар бойынша) “жіктеуге” болады, яғни мынадай түрде көрсетуге болады:

f= c ₁ ϕ ₁ + c ₂ ϕ ₂ + …+ c _i ϕ _i + …, (*)

мұндағы c ₁ , c ₂ . . . жіктеу коэффициенттері - {ϕ} базисіндегі f вектордың құраушылары (координаталары) болып табылады да, мына өрнекпен анықталады:

. (**)

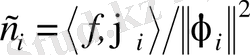(Бұл формуланы әдеттегі үшөлшемді векторды базис бойынша жіктедің өрнектерімен салыстырындар)

Сигналды Фурье-қатарына жіктеу

Cөйтіп, барлық дерлік периодты сигналдар Фурье қатарына жіктеледі. Бұл жіктелу болу үшін ұзақтығы бір периодқа тең сигналдың үзіндісі Дирихле шарттарына қанағаттандыруға тиісті:

екінші текті үзілістер (шексіздікке кететін функцияның тармақтары) болмау тиіс;
бірінші текті үзілістердің (секірулерлің) саны шектелген болу тиіс;
экстремумдардың саны шектелген болу тиіс (шектелген аралықта экстремумдерінің саны шексіз болатын функцияның мысалы (1/x) функцияны келтіруге болады.

Дирихле шарттары барлық практикада кездесетін сигналдар үшін орындалады.

Бірақ функцияның Фурье қатары функцияның өзіне тек үздіксіздік нүктелерінде жиналады, t _i үзіліс нүктелерінде ол S(t _i ) =(s(t _i +o) + s(t _i -o) ) /2 шамаға жиналады (мұндағы s(t _i +o) және s(t _i -o) - t t _i -ге сәйкесінше оң және сол жақтан ұмтылғандағы s(t) функцияның шегі, S(t) - s(t) функцияның Фурье-қатарының қосындысы) . Яғни функцияның Фурье қатары функцияға тек орта мағынада жиналады, ал егер жуықтауды сипаттайтын шама ретінде 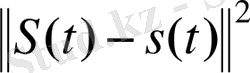шаманы, яғни қатардың функциядан квадраттық ауытқуын (еңістігін) емес, Фурье қатары қосындысының функция мәнінен ең жоғары ауытқуын алсақ, ол барлық нүктелерде нольге ұмтылмайды. Сөйтіп, сигналдың үзіліс нүктелерінде бақыланатын Гиббс эффектісі жойылмайды.

Базистік функцияларының нақты түріне байланысты Фурье-қатарын жазудың бірнеше түрін айырады. Фурье қатарының қандай түрі қолданатыны нақты сигналды жіктеу үшін қайсысы ыңғайлы болатынымен байланысты.

Синусты-косинусты түрі:

(5. 1)

Қатардың құрамына уақытқа тәуелсіз а ₀ /2 тұрақты құраушысы және гармоникалар деп аталатын гармониялық тербелістердің (синусоидалар мен косинусоидалардың) ақырсыз жиынтығы кіреді. Гармоникалардың жиіліктері сигналдың Т периодына сәйкес келетін ω ₁ = 2π /Т негізгі жиілігіне еселі болып табылады: ω _k = kω ₁ . Гармоникалар k индексіне сәйкес нөмірленеді, периоды ең жоғары тербеліс (гармоника) негізгі жиіліктің тербелісі, немесе бірінші гармоника деп аталады. Бұл гармоникалар функцияны Фурье қатарына жіктеудің базистік функциялар болып табылады. Фурье коэффициеенттері деп аталатын қатардың а _k мен b _k коэффициенттері мына формулалар бойынша есептелінеді:

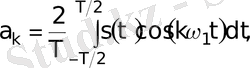
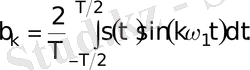
а ₀ коэффициенті а _k үшін жалпы формула көмегімен есептелінеді (демек оның жиілігі 0-ге тең, яғни ол сигналдың тұрақты құраушысы болып табылады) . Тұрақты қосылғышты жазудың екіге бөлуімен түрі бұл ортақтық болу үшін қолданылады. Бұл қосылғыш сигналдың период ішіндегі орташа мәніне тең болады:

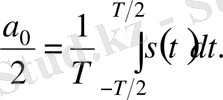
ЕСКЕРТУ

Фурье-коэффициенттері векторды базис бойынша жіктеудің жалпы формула, яғни (**) формула, бойынша есептелінеді, интеграл алдындағы 2/ Т коэффициенті Фурье қатарының базисті функцияларының (синус пен косинустардың) нормалары тең екендігімен байланысты.

Нақтылы сигнал туралы мәлімет жіктеу коэффициентерінде болады (ұсталады), бірақ олар базистік функцияларға да байланысты болады ( ушөлшемді кеңістіктегі вектордың берілген бір базистегі жіктеу коэффициенттері (құраушылары) векторды толығымен анықта ғанға ұқсас) .

Фурье-коэффициенттер үшін формулаларды екі сигналдың корреляциялық функция үшін өрнегімен салыстырсақ, k -ші коэффициент жіктеліп отырған сигналдың жиілігі kω ₁ -ге тең синусоидамен (не косинусоидамен) корреляциясын (ұқсастығын, сызықты байланысын) сипаттайтынын көреміз: егер бұл коэффициенттің мәні жоғары болса, онда біздің сигналдың сәйкесінші гармоникаға ұқсастығы, демек бұл гармониканың сигнал ішіндегі құраушысы да жоғары болады.

ЕСКЕРТУ

Интегралдау шектері жоғарыда келтірілген формулалардағыдай ( -Т /2 -ден до Т /2 -ге дейін) болу міндетті емес. Интегралдауды ұзындығы Т -ге тең кезкелген арлық бойынша жүргізуге болады - нәтиже одан өзгермейді. Нақты шектер есептеуді жүргізудің ыңғайлылығына байланысты қалап алынады, мысалы, интегралдауды 0 -ден Т -ге дейін, немесе - Т - ден 0 -ге дейін орындауға ыңғайлы болуы мүмкін.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.