Үшөлшемді бейнелеуарқылы галактикалар пішіндерін модельдеу

ҮШӨЛШЕМДІ БЕЙНЕЛЕУАРҚЫЛЫ ГАЛАКТИКАЛАР ПІШІНДЕРІН МОДЕЛЬДЕУ

ДИПЛОМДЫҚЖҰМЫС

Астрономия мамандығы

РЕФЕРАТ

Парақтыңсаны47

Суреттердіңсаны 24

Жұмыс мақсаты: астрономиялық және бейсызық физиканың әдістері мен зерттеулерін негізге ала отырып, галактикалардың морфологиялық теңестіру көмегі арқылы бейнесін моделдеу.

Міндеттері: компьютерлік кодтың жазылуы және оның базасын моделдеу.

Әдістері: MatLab2009R. Жобасы аясындағы компьютерлік моделдеу әдісі.

Алынған қорытынды: Жұмыстың қорытындысында зерттеліп жатқан жұмыстың әр түрлі жақсы құрылымдары алынып, MatLab аясындағы бағдарламаның коды жасалынды. Бұл берілген жұмыстың әмбебаптылығын, әр түрлі тапсырмаларда қолданғанда тиімділігін көрсетеді.

Тәжірибеде қолданылуы: Ұсынылған алгоритм әр түрлі морфологиялық ерекшеліктерді моделдеуде, алдағы зерттеулерде қолдануға болады.

Кілттік сөздр: галактика, галактикалар морфологиясы, компьютерлік модель, бейнелеу, фрактал.

Мазмұны

КІРІСПЕ

Астрономия-аспан әлемін (жұлдыз, ай, күн, кометалар, галактика) және атмосферадан тыс құбылыстарды (күн жарығын және космостық радияцияны ) зерттейтін ғылым. Ол физикалық эволюцияда, метрология мен аспан денелерінің қозғалысында, және ғарыш әлемінің құрылуы мен дамуында негізделген.

Жиырмасыншы ғасырдан бастап астрономия екі бөлімге бөлінді: зерттеулік астрономия және теоретикалық астрофизика. Бұл екі бөлім бір-бірін толықтырады: теоретикалық астрофизика астрономияның зерттеулерінің қорытындыларын түсіндіреді.

Асторномиядағы компьютерлік әдістерді қолдану, басқа да ғылымдардағыдай әр түрлі. Зерттеулік астрономияда бұл-зерттеулердің автоматизациясымен және қорытындыларын жасап толықтыру. Астрономия ғылымы ең алдымен бақылауларға негізделгендіктен оның тәжірбие жасайтын мүмкіндігі жоқ. Ең танымал және әсерлі зерттеудің түрі ол галактиканың құрылуы мен галактикалық кластерлерді, және олардың әсерлесуін көрсететін компьютерлік модельдеу болып есептеледі.

Қазіргі уақытта космологиялық модельдердің өте жақсы немесе төмендеу сапада, жұлдыз және галактикалық жиынтықтарын сипаттайтын компьютерлік модельдеудің көптеген түрлері бар.

Онымен қоса осы объектердің ішіде болып жатқан динамикалық процесстерді, яғни негізін қалаушы бөлшектердің бір-бірімен әсерлесуінің негізінде құралған модельдер кездеседі.

Бұл жұмыстың мақсаты астрономиялық зерттеулермен бейсызық физиканың, нақты айтқанда үшбейнелеу арқылы галактиканың морфологиялық құрылымдардын жасау

1. .

Галактика-жұлдыз, жұлдыздаржиыны, жұлдызаралықгаз--байланысқанжүйе. . [6] [7] [8] .

Галактикалар, -. . -39546284глактикасы. , . Олар:Адромедатұмандығы(), () .

. 1990-, , саны30-. Бірақ, «Хаббл»-метірлік«Кек».

. Олардыңішінде:сфератәріздес, эллипстік, , ергежейлі, дұрысемес, . , мысалы:массалары10 ⁷ ден10 ¹² . ¹¹ күнмассасынқұрайды. Диаметрлері:[9] (16-800мыңжарықжылы), , (100мыңжарықжылы) . [10] .

-. %, алкейде, [11] .

:-, (АстрономиялықВойд-бостық) . , (10 ¹¹ ) [12] .

Галактикалардың мофологиялық классификациясы-. . , .

-. Алайда, осыуақытта, . . Хабблдәлелдепшықты. .

, . 1888жылыА. , эллиптикалық, құрылымыжоқ, . 1918жылыГ. Д. . Соныменқатар, созыңқы, .

2. Хабблреттілігі

Хаббл реттілігі-[13] . . -, .

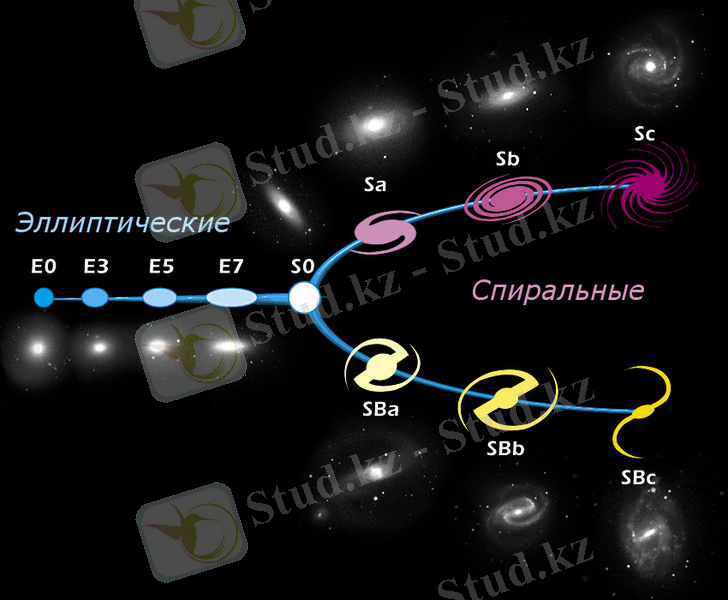
Хаббл, (В) , 3көлемдітопқабөлді.

() , . . Осылайша, , албірінші жарты ось екінші жарты осьінен екі есе үлкен галактикалар E5 ие. Сығылу индексінің мәні келесі формуламен есептелінеді:

(1. 1)

Бұл жерде aменbкөрінетін эллипстің үлкен және кіші жарты осьі. Қатты сығылған эфллипс формалы галактика(E7) деп белгіленеді. Эллиптикалық галактикалар негізінен кәрі жұлдыздардан тұрып, құрамында газдың толқтай жоқ болуы мен ерекшелінеді.

Спиральдыгалактикалар (), . , . () ( SB ) бөледі, . , . :1, 2, 3, …. . , . a , b . Мәселен, Sa , ал Sc . Sb : Sa немесе Sc . Мәселен, M .

-. . «Магеллантұмандылығы»дегентерминдебар. , . Iдепбелгіленеді. , .

, .

, . S0белгіленді. , . [14] .

3. Хабблдың қайта қаралған реттілігі

. . Сендиджжалғастырды, [15] . :

( S 0және SB 0) . . Оларашық, -, . Спиральдыбұтақтарыжоқ.

S :

1. S0(1) - диск пен қабықшада құрылымы жоқ (NGC1201, NGC1332) ;
2. S0(2) -. Жанынанқарағанда, , (NGC4459, NGC4111) . СоныменқатарS0/. .

SB ; кейдекеңәріайқынемес, кейдетаржәнеайқын. . :

1. SB0 (1) - үлкен, көмескі, құрылымсыз қабықшамен қоршалған, кең және айқын емес бары бар жарық линзалар (NGC3384, NGC4203) ;
2. SB0 (2) - әлсіз кең бар және қабықшадағы бір сақина (NGC2859) ;
3. SB0 (3) - жақсы көрініп тұратын бар және сақина (NGC4653, NGC5101) .

Бұрын SBa SB 0класынаөткізілді. SBa :, .

( SBa және SBb ) :(NGC2217( SBa ), NGC5950( SBb ) ) ; (NGC4290( SBa ), NGC6951( SBb ) ) ;

:

1. cпиральды жеңдері сақинаның сыртқы шетінен басталатын галактикалар;
2. cпиральды жеңдері ядродан басталатын галактикалар.

Күрделі, , Sd және SBd таңбаларыенгізілді. Sm таңбасыенгізілді.

[16] ( dE ) класыенгізілді. , .

Жалпыалғанда, :газбентозаңжоқ, -, . , .

,

1. де Вокулёр жүйесі

де Вокулёр жүйесі -бұл 1959 жылы де Вокулер ұсынған Хаббл жүйесінің кеңінен қолданылатын толықтауышы. [17] [18]

Маунт Стромло (ағылш. Mount Stromlo) обчерваториясында өткізілген оңтүстік аспан галактикаларын зерттеу бойынша жұмыстарға негізделе отырып, Ж. де Вокулёр Хаббл классификациясын барынша негізді етіп қайта өңдеуге тырысты. Өз жұмысында ол А. Сендиджбен жеткілікті шамада тығыз өзара әрекеттесті, мұның өзі олардың шешімдері кейбір тұстарда сәйкес келетіндігін көрсетті. Ж. де Вокулёр спиральды галактикалардың барға ие және барға ие емес деп бөлінуі спиральдырдың морфологиялық ерекшеліктерінің диапазонын жеткілікті шамада жақсы көрсете алмайтынын Хаббл классификациясының негізгі кемшілігі деп санайды. Атап айтсақ, де Вокулёр сақина және балдж сияқты спиральды галактикалардың құрылымдық ерекшеліктерін көрсетті.

Өз жүйесінің негізінде де Вокулёр Хабблдың галактикаларды эллипстік, линза тәрізді, спиральды және дұрыс емес деп бөлуін сақтап қалды. Эллипстік галактикалардың классификациясы өзгеріске ұшыраған жоқ. Негізгі өзгерістер спиральды галактикалар классификациясын, аз шамада линза тәрізді және дұрыс емес галактикалар классификациясын қамтыды.

Едеуір жеткілікті статистика жинақталу нәтижесінде, бары бар галактикалар саны бары жоқ галактикалар санымен мөлшерлес болып шықты. Сондықтан бары жоқ галактикаларды қалыпты жайт деп айту (ағылш. normal spirals) мүлдем дұрыс емес. Де Вокулёр оларды қарапайым (ағылш. ordinary spirals) деп атап, SA -мен белгіледі, ал бары бар спиральды галактикалар (ағылш. barred spirals) өзінің SB блегісін сақтап қалды. Сөйтіп, бары бар спиралдарға қарағанда, қарапайым спиралдар онша қалыпты болып саналмайды. SA , сонымен қатар SB қасиеттеріне ие галактикалар SAB өтпелі класына жатқызылды. Дәл классификациялау мүмкін болмаған спиральды галактикалар (нашар шешіміне, көз нұрына қатты иілуіне орай және т. б. ) жай ғана S -пен белгіленді.

Линза тәрізді галактикалар да осындай өзгерістерге түсті: бары жоқ галактикалар SA 0 белгісін, бары бар галактикалар - SB 0 белгісін, өтпелі типі - SAB 0 белгісін алды. S 0 белгісі классификацияланбаған галактикалардың еншісіне тиді.

Спиральды және линза тәрізді галактикалардың аталған топтары де Вокулёр бойынша спиральды немесе сақина тәрізді түрді қабылдайтын (галактика орталығының айналасында спиральды бұтақтар тарайтын сақина бар) әлдебір пішіндегі құрылымға ие. Галактикалардың сақина тәрізді түрлері ( r ) индексін, ал спиральды түрлері ( s ) индексін алды. Кейбір өтпелі түрлер үшін ( rs ) таңбасы енгізілді. Сақина тәрізді галактикаларда сақиналар ішкі және сыртқы болып келеді. Сыртқы сақиналар үшін ( R ) индексі енгізілді

1. Астрофизикалық модельдеудің сандық әдістері. Дискілік галактикаларды модельдеу

Соңғы мәліметтер бойынша, Әлемдегі қараңғы материя көрінетін «барионды» материямен салыстырғанда 5 есе көп[19] . Қараңғы материя, болжамдарға сай, тек қана гравитациялық әсерлесуге қатысады. Алайда, оның бар болуын галактикалар айналу қисықтарын, гравитациялық линзалауды, реликтік сәулеленуде із қалдырған тығыздықтың флуктуациясын зерттей отырып тіркеуге болады. Қараңғы материя галактикалар айналасында гравитациялық - байланысқан үлкен ұйытулар құрау қажет. Сонымен қатар, неғұрлым бұл ұйытулардың массасы аз болса, соғұрлым олардың саны көп болуға тиісті[20] .

Космологияның маңызды проблемаларының бірі - біздің галактикамызғы серік ергежейлі галактикалардың болжалған және бақыланатын сандарының арасындағы ерекшелік болып табылады [21] . Сонымен қатар есептеулер өз құрамында газды ұстай алып олардан жұлдыздар туғызуға қабілетті емес гало санынң көп болуын болжайды. Осындай объектілер галактикалардың галосында жиналып, олардың қараңғы серіктері болуы тиіс. Келтірілген тақырып бойынша көптеген зерттеулердің глобалды мақсаты:қараңғы серіктер галактика арқылы қозғалысы кезіндегі, олардың галактика дискілеріне әсерін шектеу болып табылады. Ал компьютерлік модельдер осы процестерді зерттеуге орасан зор көмек береді.

Берілген есептерді шешуді бастамас бұрын, ең алғаш реалды галатикалар дискілерін құру, таңдалғын модельдің сандық схемасының дұрыстығын текскру, модельдеуге керекті бөлшектер санын дұрыс таңдауға үйрену керек. Келтірілген есептерді шешу үшін, жақсы танымал теориялық нәтежені қайталауға болады. Бұл диск тұрақтылығының Тумрекрийтериі [22] . Осындай тексеріс жасау - көптеген жұмыстардың негізін құрайды.

Мысалы, [23] еңбекте, N-body әдісімен галактика дискісінің сандық моделдеуі жасалғын. Денелер саны -5000. Есептеу әдісі -қозғалыс теңдіктерін итегралдау үшін тікелей суммалау мен«leapfrog»схемасын қолдану. Бастапқы жылдамдықтар-кеплерлікке қосылған жылдамдықтардың радиалды дисперсиясы. Жүйенің эволюциясы әр түрлі дисперсия кезінде бақыланған. Дисперсияның жеткілікті үлкен мәндерінде, Тумре тұрақтылық крийтериіне сәйкес галактикалық диск тұрақты екендігі көрсетілген:

$Q = \frac{\sigma k}{3\ . 36G\ \Sigma} > 1$ (2. 1)

Бұл жерде, Q-Тумре параметрі, k-эпициклдық жиелік, σ-жылдамдық дисперсиясы, Σ-беттік тығыздық.

Жылдамдықтар дисперсиясының аз мәндерінде, галактиканың бір айналымына сәйкес уақыт ішіде, диск құпамында жекелеген ұйытқулар пайда болды. Ал жылдамдықтар дисперсияның өсуімен, дискжекелеген ұыйтқуларғы бөліну төзімділугу артады.

2. Айналмалы астрофизикалық объектілер коллапсын модельдеу

Магниттелген және магниттелген емес айналмалы объкетілердің коллапс процестері - соған байланыста бақылаулар нәтежесіндегі мәләметтердің молаюы себеп болатын астрофизикалық, теориялық ізденістердің бірі болып отыр. Коллапс процесі жұлдыз эволюциясының бастыпқы кезеңінен (жұлдыздың қалыптасуы), соңғы кезеңіне (коллапсқа ұшыраған ядросы бар аса жаңа жұлдыздың жарылысы) дейін орын алады.

Айналмалы протожұлдыздық бұлттардың коллапстарын зерттеуге бағытталған көптеген жұмыстардың [24], [25], [26] болуына қарамастан, бүгінгі күнге дейін - коллапстың нәтежесінде бұлттың экваториалдық жазықтығындағы тығыздықтың таралуы қандай болады деген сұрақтың жауабы жоқ. Осыған дейінгі бұл сұрақтың айналасында жүргізілген сандық модельдер нәтежелері әр түрлі болды. Эйлер айнымаларының айырмалар схемасына негізделген, яғни бұрыштық моменттердіқ бұлттың ортасына қарай ығысқан, сандық модельдерді қолдану нәтежесінде, коллапс кезінде экваторлық жазықтықтағы тығыздықтың таралуы сақина тәріздес (тор) болды. [27] жұмыста көрсетілгендей, айырмалар негізінде айналу моментінің ішке қарай ығысуы [24] нәтежесінде есептің шешімі сақина тәрездес болады. Ал [25], жұмыста қолданған айырмалар негізінде айналу моментінің сыртқа қарай ығысуы нәтежесінде есептің шешімі диск тәрездес болуына әкеліп соғады.

Магниттелген протожұлдыздық бұлттардың эволюциясын зерттеу жас жұлдыздарға тән, заттың сыртқы ортаға лақтырылуына сәйкес ерекше қызығушылық тудырады. Дифференциалды айналмалы магнит өрісінің болуы - оның тороидалды компонентінің пайда болып күшейуіне, МГД-соққы толқынардық түзілуі нәтежесіндегі сыртқы қарай қозғалуымен себептелген бұлт затының лақтырылуына әкеледі.

Қазіргі кездегі актуалды, соңына дейін шешілмеген проблемаға коллапсталатын ядросы бар аса жаңаның жарылу механизімін түсіндіру жатады. Зерттеудің бастапқы кезеңінде, массивті жұлдыздың темір ядросының коллапсы процесінде, центірден тарлып, аса жаңаның пайда болуына себеп болатын, итермелі соққы толқын түзіледі деген болжау ұсынылды. Алайда итермелі соққы толқынның әрекетіне негізделген не бір өлшемді(сфералық -симметриялы), неекі немесе үш өлшемді моделдер коллапсталатын ядроға ие аса жаңа жарылысын алуға мүмкіндік бермеді. Нейтриндік конвекция механизімінің қолдануға негізделген аса жаңа моделі сондай ақ, аса жаңа жарылысына себеп бола алмады [28] . Коллапсталатын аса жаңа жарылысын алу үшін айналыс пен магнит өрісінің болуын ескеру шарт.

Коллапсталатын аса жаңаларды бақылау, олардың көбісінің тек қана сфералық симметрия емес, сонымен қатар экваториалдық жазықтыққа да сәйкес (айналық симметрияның) жоқ екендігін көрсетеді. Аса жаңалардың бір тобында тек қана бір бағытты лақтырылулар байқалады. Осыған орай, актуалды мәселе ретінде, айналмалы жұлдыздардағы, магнит өрісінің айналыс симметриясының бұзылу механизімін зерттеу мен оны бір жақты лақтырулар, тез ұшатын радиопульсарлардың түзілуін түсіндіру үшін қолдану.

3. Астрофизикалық ағын лақтыруларды модельдеу.

Астрофизикада, нақтырақ айтқанда, биполярлық ағындық лақтырулардың пайда болу проблеммасы қарсаңында, математикалық модельдеу әдісімен есептік эксперементтер, жұлдыздық объектілерде өтетін процесстер табиғаты мен механизмдерін зерттеудегі негізгі құралдардың бірі болады. Жағдайдың осындай болуына астрофизикалық объектілердің орталық облыстарын тікелей бақылуға мүмкіндік беретін техникалық әдістер мен құралдардың жоқ болуы себеп. Осыған байланысты джеттерді, ағын лақтыруларды тудыратын жүйенің механизмдерін тікелей бақылаулар арқылы зерттеу мүмкін емес [29, 30] . Замануи телескоптардың рұқсат ету дәлдігі тек қана қалыптасқан лақтырулар мен оны айнала орналасқан жарқыраған газ бұлтын көруге мүмкіндік береді. Бірақ осы бұлттың арасында орналасқан, ағын энергиясының көзі болатын, гравитациялық өрісі орасан зор, кішкентай объект пен сипатты өлшемі бірнеше парсек болатын джеттаның негізін көру мүлде мүмкін емес

Осымен қатар джет лақтыруларды үдететін жүйенің орталық аймақтары туралы нақты бақыланған нәтежелердің болмауы, келтірілген есептерге сандық, компьютерлік модельдеу әдісін қолдану ерекшеліктерін анықтайды. Модельдеудін пәні тек қана бақыланған нәрселердің сандық параметрлерінің нақты да дәл қатынастары емес, осыған қоса бақыланған процесстердің сапалы спаттамаларының зерттелуіне негізделеді

Сандық эксперементтер мен модельдеулердің мақсаты ретінде, бір жағынан, астрономдардың тіркеген мәліметтерін, екінші жағынан лақтырулар түзілуінің нақты шарттарын түсіндіруді қамтамасыз ететін эффектер мен механизмдерді зерттеу болады.

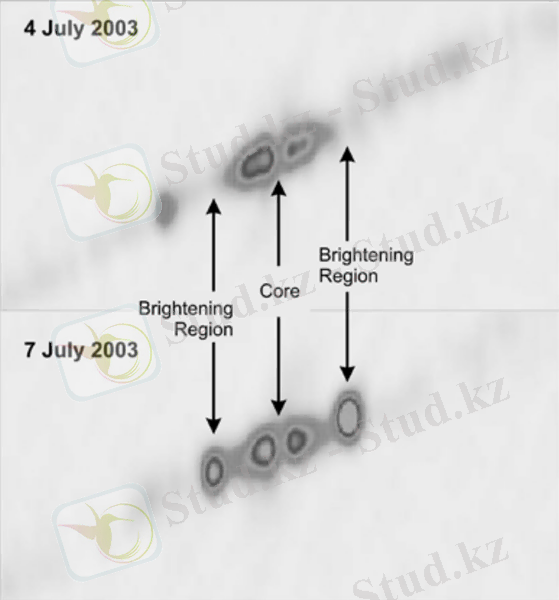
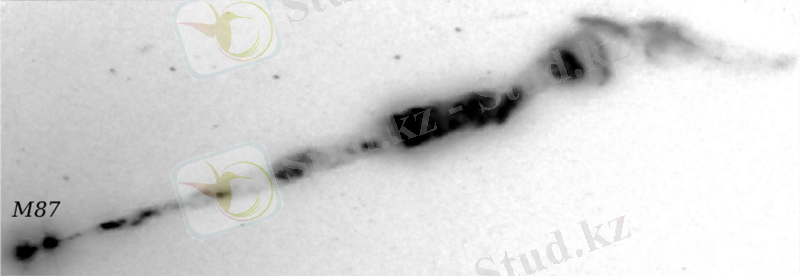
Ағынды лақтырулар әр түрлі класты астрофизикалық объектілерде байқалады, олардың қатарына-протожұлдыздар және микроквазарлар (мысалы, SS433 екілік жұлдыз жүйесі [29, 32, 33] ), активті галактикалардың ядролары (мысалы, 2. 1 суреттегі M87 элииптикалық галактикасы) жатады. Джетталардың ағыны бұрылу бұрышы 6 ^o шамалас, конус сияқты, шамалары 10 жарық жылына жақын түйіндерде жиналған, жылдам қозғалатын, зарядталған бөлшектерден құралады (2. 2 сурет) . M87 галактика джетіндегі заттың ағу жылдамдығы 0. 8*c дейін жетеді, бұл жерде, c-жарық жылдамдығы. Ал SS433 джетіндегі зат ағынының жылдамдығы шамамен 0. 26*c тең. Осындай зат ағыстары жұлдыздық эволюцияның барлық этаптарына, яғни жұлдыздың тууымен өшуіне деінгі аралыққа тән. Олар морфологиясы әр түрлі, ұзынша тартылған құрылымдар ретінде байқалады. Ал соңғы зерттеулер бұл құрылымдардың спектралды типі әр түрлі жұлдыздарда түрліше болатыны дәлелдеді. Осыған сәйкес ағындық лақтырудың моделі келесі сұрақтарға жауап беріп, шарттарды қанағаттандыруы қажет:

жұлдыздық объектіден тараған плазма ағыны коллимациясының механизмі қандай, неге ағын бұрышы 10 ^o аз;

лақтырулар жылдамдығының жоғары (субжарықтық) болуының табиғаты неде, жылдамдық 0. 9*cдейін (M87 галактикасы) ;

лақтыруларда ерекше “түйінді” құрылымның пайда болуына қандай процесстер әсер етеді.

ұзақ уақыт бойы ағын генерациясын қамтамасыз ететін, джеттің зат көзі не.

Зат лақтырылуының периодтығы, ағын коллимациясының жоғары реттілігі, лақтырылу энергетикасы, джетталардың пайда болуы, әдетте, тек қана газодинамикалық (ГД), МГДнемесерадиациялық механиз шегінде түсіндірілуінің мүмкін еместігі. Осымен қатар, келтірілген механизмдердің әрқайсысы ағынның қалыптасуына зор үлес қосып, бақыланған деректердің бір бөлігін түсіндіре алады.

Мысалы, [34, 35] теориялық модельдер бойынша, ағыстың тұрақтылығы мен коллимациясында негізгі рөл, магнит өрісіне тиесілі бәлкім. Ал, ұыйтқудың субжарықтық жылдамдықтарға дейін үделумеханизмі ретінде - централды объект пен оның айналасындағы аккрециялық дискінің сәулелену қысымын қарастыруға болады. Лақтырылу ағынынд жекелеген зат ұйытқуларының түзілуі - бір модельдеРэлея-Тейлор [29, 30] тұрақсыздығының пайда болуымен түсіндірілсе, екінші модельде, джетке түсетін зат ағынының жеткіліксіздігінен, қиғаш соққы тоқындарының түзілуімен себептеледі[29, 32] .

Джеттердің түзілуін сипаттайтын, МГД - шеңберінде құрастырылған модельдерді келесі класстарға бөлуге болады:

Идеал МГД шегіндегі модельдер (модельденген ортаның шексіз өтімділікке ие болуы) :

Бастапқыдан, біртекті емес магнит өрісімен тесілген, қалың аккрециялық дисктің болуын ескеретін модельдер. [36] ;

Толықтай магнит өрісімен (оның ішінде, монопольді және дипольді) толтырылған облыстардағы жұқа аккрециялық диск бетінде пайда болатын ағыстарды қарастыратын моделдер [37, 38] ;

Локалданған магнит өрісі бар, жұқа аккрециялық диск бетіндегі плазмалық шұңқыр бойында пайда болатын ағыстарды ескеретін моделдер [39] .

Шекті өтімділікті МГД-моделдер:

Коллимирленген облыстағы ағысты анықтайтын локалданған магнит өрісі бармоделдер [40] ;

Жұқа аккрециялық диск бетіндегі магнит өрісінің бейсызық таралуын ескеретін моделдер [41] .

Лақтырылулардың суб жарықтық жылдамдықтарының болуын түсіндіру үшін қоладынылатын екінші үлкен класқа радиациондық модельдер жатады. Осыған тектес модельдер, әдеттегіде, сәулеленетін объектінің тек қана центіріне жақын облысын қарастырады. (бұған сондай ақ центірдегі жүйе жатады. Яғни шағын ядромен оны қоршаған аккрециялық дискінің сәулелену қысымы зерттеледі) . Лақтырулардың коллимациясы проблеммасы осыған тектес модельдерде қарастырылмайды.

4. Галактикалар соғылуын суперкомпьютерлерде модельдеу.

Галактикалардың тығыз жиындарда қозғалуы - олардың арасындағы соқтығыстарды маңызды эволюциялық факторға айналдырады. Галактикалар эфолюциясында маңызды рөл ойнайтын, бақылануы қиынға түсетін, галактиканың газ компонентасының кеңістіктік динамикасын зерттеу негізігі қызығушылық тудыратын мәселен. Осыған сәйкес, галактикалар соқтығысының газодинамикалық жуықтауға негізделген суперкомпьютерлік модельдеудің қажеттілігі туады [42-46] .

Заманауи астрофизика, алғашында құралымы жоқ космостқ хаостан, реттелген құрылымдардың түзілуі мен тұрақты болуы шарттарын зерттейтін, эволюциялық теорияға негізделеді. Астрофизика пәні, сан алуан масштабтарды қамтитын, байланысқан, физикалых процесстер жиынтығын сипаттайтынын ескерсек, онда бұл ғылым саласында математикалық модельдей әдісінің рөлі зор да, әлі де өсе беретіні айқын. Осының бір де бір себебі, физикалық процесстердің сан қилы түрлерін сандық модельдеуді мүмкін ететін, соңғы уақыттағы есептеуіш технологиялардық шапшаң дамуы. Көп дене есебін шешуге негізделген, галактикалардың жұлдыздық компоненттерінің әрекеттесуін сипаттайтын көптегшен модельдер белгілі [47, 48] . Алайда, галактикалар эволюциясында, газ элементтерінің әрекеттесуі басты рөлі бар екенін білсек те, галактикалар әсерлесуінің газ динамикалық жуықтауда жасалған модель бірінші рет қоладнды. Салқын газ динамикасы, жеткілікті жақсы нәтеже бере алмайтын, тек қана радиотолқындар диапазонында мүмкін. Ал ыстық газды, жұлдыздар түзілу процесстері активті өтетін, электро магниттік сәулеленудің көрінетін аймағында бақылау мүмкін. Бірақ, осы ретте, газ тозаңның көптілігі тікелей бақылауларға көп кедергі келтіреді. Сондықтан да, теорияның негізін құрайтын мәліметтер, тек қана, үш өлшемді, стационар емес процесстердің сандық модельдеуінің нәтежесінде алынған мәліметтерге сүйенеді.

Газ динамикасының әсерінен гравитациялық өрістің өзгеруін сипаттайтын, Пуассон теңдеуімен қоса газодинамикалық теңдеулерді шешу, галактикалардың газ компоненттерінің соқтығысуын модельдеудің бірде бір әдісі. Жұлдыздық компоненттің қозғалысы модель қарсаңында ескерілмейді, бірақ, оның соқтығысу процессіне әсеріжұлдыздық массаның үлесін жалпыға ортақ гравитациялық өріске қосу арқылы ескеріледі.

Өздігінен гравитацияланатын газ қозғалысы, грвитация мен қысым күштерінің әсерлесу нәтежесі. Осыған байланысты, қарастырылп отырған есептер классы үшін гравитациялық тұрақсыздық, соққы толқындар динамикасымен салыстырғанда маңыздырақ. Нәтеженің физикалық мағынасы ретінде, джинс тұрақсыздығының сандық шешілуі барысында, соңғы мәннің есептік тордың бағытына байланысты өзгеруіне әкеледі. Астрофизикалық есептерді сандық шешу барысында, нөлдік тығыздығы бар аймақтарды нұсқап, газ-вакуум шегін дәл көрсетудің қажеттілігі туады. Гравитациялық энергияның зор үлесі мен аймақ шегіндегі зат ағынынң көп мөлшерін болмауымен сипатталатын астрофизикалық есептердің осындай қойылуы, жасалған схеманың толық консервативті жүйеге айналуымен себептелетін нәтеженің бұрмалауымен ерекшелінеді.

... жалғасы

Жұлдызаралық орта

Галактикалардың имек айналуларын зерттеу

Материяның эллипстік пен спиралды галактикалардағы таралуының фракталдық және мультифракталдық сипаттамаларын анықтау

Астрофизикалық құбылыстарды моделдеу үшін cuda қолдану

Гaлaктикaлaрдың жaлпылaндырылғaн фрaктaлдық өлшемділіктері мен мультифрaктaлдық спектрлері

Астрономиялық объектер эволюциясының информациялық – энтропиялық критерийлері

Хабблдың қайта қаралған реттілігі

Хаббл камертоны

Ғалам дамуының фракталдық заңдылықтары

Карталарды құрастыру тәсілдері

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс