Астрономиялық объектер эволюциясының информациялық – энтропиялық критерийлері

Пән: Астрономия
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 62 бет
Таңдаулыға:

«АСТРОНОМИЯЛЫҚ ОБЪЕКТЕР ЭВОЛЮЦИЯСЫНЫҢ ИНФОРМАЦИЯЛЫҚ - ЭНТРОПИЯЛЫҚ КРИТЕРИЙЛЕРІ»

тақырыбында

ДИПЛОМ ЖҰМЫСЫ

РЕФЕРАТ

Дипломдық жұмыстың құрамы:

Беттер саны 58
Суреттер саны 26
Пайдаланылған әдебиеттер саны 34

Негізгі ұғымдар: энтропия, информация, информациялық - энтропиялық талдау, галактика, эволюция, жалпыландырылған метрикалық сипаттама.

Зерттелетін объектер: галактикалар бейнесі.

Дипломдық жұмыстың мақсаты: галактикалар эволюциясын бейсызық физика әдістерін қолданып зерттеу

Зерттеу әдістері MatLab компьютерлік модельдеу ортасында, әр түрлі галактика типтері үшін, энтропия-метрикалық диаграмманы тұрғызу арқылы жүргізілді.

Алынған нәтижелер: галактикалар дамуының энтропиялық - метрикалық диаграммасы, осының нәтижесінде эволюцияның өту бағыты.

МАЗМҰНЫ

КІРІСПЕ1 ТЕОРИЯЛЫҚ БӨЛІМ . . . 5Галактикалар классификациясы……. . . . . 5Хаббл реттілігі. . 6Хабблдың қайта қаралған реттілігі . . . …… . . . 10Ж. де Вокулёр жүйесі. . 121. 2. 1 Фракталдар . . . ……14Энтропия түсінігі. ……. 202 ИНФОРМАЦИЯЛЫҚ ЭНТРОПИЯ. 232. 1 Теңсіздік статистикалық жүйенің өзаффинді және өзұқсастығының информация-энтропиялы критерилері232. 2 Ашық жүйелер эволюциясының әмбебап энтропиялықЗаңдылықтары . . . 252. 3 Хаостық сигналдардың формасының екіөлшемді коэффициенті…. 292. 4 Корреляциялық өлшемділік. …. . 302. 5 Динамикалық жүйелердің энтропиясы . . . 332. 6 Біртектілік дәрежесі ескерілген екі өлшемді объекттің информациялық энтропиясы . . . 363 АЛЫНҒАН НӘТИЖЕЛЕР . . . 373. 1 Геометриялық фигуралардың энтропиясы373. 2 Екі өлшемді фракталдық объектер энтропиясы423. 3 Галактикалар үшін энтропиялық диаграмма тұрғызу. 44ҚОРЫТЫНДЫ . . . 49ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 50ҚОСЫМША А . . . . . . 52ҚОСЫМША Ә . . . 54ҚОСЫМША Б . . . ……. 55ҚОСЫМША В . . . …. …56ҚОСЫМША Г . . . …. …58:

КІРІСПЕ

1 ТЕОРИЯЛЫҚ БӨЛІМ . . . 5

Галактикалар классификациясы……. . . . . 5
Хаббл реттілігі. . 6
Хабблдың қайта қаралған реттілігі . . . …… . . . 10
Ж. де Вокулёр жүйесі. . 12

1. 2. 1 Фракталдар . . . ……14

Энтропия түсінігі. ……. 20

2 ИНФОРМАЦИЯЛЫҚ ЭНТРОПИЯ. 23

2. 1 Теңсіздік статистикалық жүйенің өзаффинді және өзұқсастығының информация-энтропиялы критерилері23

2. 2 Ашық жүйелер эволюциясының әмбебап энтропиялық

Заңдылықтары . . . 25

2. 3 Хаостық сигналдардың формасының екіөлшемді коэффициенті…. 29

2. 4 Корреляциялық өлшемділік. …. . 30

2. 5 Динамикалық жүйелердің энтропиясы . . . 33

2. 6 Біртектілік дәрежесі ескерілген екі өлшемді объекттің информациялық энтропиясы . . . 36

3 АЛЫНҒАН НӘТИЖЕЛЕР . . . 37

3. 1 Геометриялық фигуралардың энтропиясы37

3. 2 Екі өлшемді фракталдық объектер энтропиясы42

3. 3 Галактикалар үшін энтропиялық диаграмма тұрғызу. 44

ҚОРЫТЫНДЫ . . . 49

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 50

ҚОСЫМША А . . . . . . 52

ҚОСЫМША Ә . . . 54

ҚОСЫМША Б . . . ……. 55

ҚОСЫМША В . . . …. …56

ҚОСЫМША Г . . . …. …58

КІРІСПЕ

Аспан денелерінің пайда болуы мен эволюциясы астрономия ғылымының Космогония бөлімінде қарастырылады. Космогониялық проблеммалар қазіргі уақытта тек қана астрономдардың ғана емес, барлық ғалымдардың ойын өзіне қаратады[1 -13] . «Әлем қалай пайда болды? Болашақта не болады ?» деген сұрақтарға жауап беру, адамдардың әлемге көзқарасын қалыптастырады. Сонымен қатар космогония проблеммалары - шешімі ең қиын астрономиялық есептер болып табылады. Шынында да біздің бақылайтын аспан, - әлемнің бір мезгіл суреті. Бұл арқылы «әлем қазіргі кезде қандай ?» деген сұраққа жауап бере аламыз. Ал оның өткен уақыттағы бейнесі мен болашағын болжау қиын. Бірақ соңғы уақытта аспан денелерінің пайда болуы мен дамуы туралы көп мәлімет алдық.

Космогониялық проблеммаларды шешу үшін негізгі екі бағыт бар. Біріншісі таза теориялық: физиканың жалпы заңдарына сүйене отырып, аспан денелері бүгінгі күйде болуы үшін, өткен кезде олардың сипаттамалары қандай болуы қажеттігін болжау. Екіншісі бақылау жолымен: әр түрлі даму деңгейіндегі аспан объектілерінің сипаттамаларын салыстыру арқылы, денгейлердің ретін анықтау. Соңғы бағытты көптеген объектерге қолдануға болады, соның ішінде жұлдыздар, газ тұмандықтар, галактикалар. Біз жұмысымызда осы әдісті қолданамыз.

Соңғы уақытта жалпы физиканың тармағы - бейсызық физика қарқынды дамып келе жатыр. Бейсызық физика аппараты арқылы көптеген табиғи процестердің жалпы маштабтық инвариантты сипаттамалары анықталды. Биофизика, астрономия, электроника, кибернетика, социология сияқты пәндерді байланыстыра алатын жалпыға ортақ ережелер дүниеге келді. Информация, энтропия, фрактал, фракталдық өлшемділік терминдері ғылымға енгізілді.

Жұмыстың мақсаты бейсызық физиканың жаңа әдістері және компьютерлік модельдеудің көмегімен тұмандықтар мен галактикалардың эволюциясының энтропиялық диаграммасын тұрғызу. Осыған сүйене отырып глакатикалардың даму бағытын болжау.

1 ТЕОРИЯЛЫҚ БӨЛІМ

1. 1. 1 Галактикалар классификациясы

Галактика дегеніміз - бұл шамамен 200 млрд. жұлдыздан құралатын алып жұлдыз жүйесі (олардың ішіне біздің Күн де кіреді) . Мұнда сонымен қатар газ бен тозаңның да маңызды мөлшері бар; галактика магниттік өрістермен безендірілген, жоғарғы энергиялардың бөлшектері - ғарыш сәулелерімен толтырылған.

Галактикалардың морфологиялық классификациясы - астрономияда пайдаланылатын көзбен көру белгілері бойынша галактикаларды топтарға бөлу жүйесі. Галактикаларды морфологиялық типтерге бөлудің бірнеше схемасы бар. Оның ішінде ең танымалын Эдвин Хаббл ұсынды, соңынан оны Жерар де Вокулер мен Алан Синддиж дамыта түсті.

Галактиканы классификациялау талпыныстары спиральды өрнегі бар алғашқы тұмандылықтардың табылуымен бір мезгілде Лорд Росс тарапынан 1845-1850 жылдары бастау алды. Ол кезде барлық тұмандылықтар біздің Галактикамызға тиесілі деген теория басымдық танытатын. Бірқатар тұмандылықтар галактикалық емес табиғатқа ие болатындығын Хаббл ғана 1924 жылы дәлелдей алды. Сөйтіп, галактикаларды сондай-ақ галактикалық тұмандылықтар деп те классификациялады.

Бұрынғы фотографиялық шолуларда спиральды тұмандылықтар басым болды, мұның өзі оларды жеке класқа бөлуге мүмкіндік берді. 1888 жылы А. Робертс аспанға терең шолу жасап, нәтижесінде көптеген эллипстік құрылымсыз және өте созылыңқы ұршық тәрізді тұмандылықтар табылды. 1918 жылы Г. Д. Кёртис тосқауылды және сақина тәрізді құрылымды спиральдарды жеке Ф-тобына бөлді. Сонымен қатар ол ұршық тәрізді тұмандылықты қабырғадан көрінетін спиральдар ретінде түсіндірді.

Гарвард классификациясы. Бұрын пайдаланылып келген классификациялар статистикалық зерттеулер үшін онша жарамды болмай қалды. Негізінен, бұл әлсіз галактикалардың көріністеріндегі бөлшектерді айқындау қиындықтарына байланысты еді. Сонымен қатар Гарвард обсерваториясының негізгі аспабы 24-дюймдік (≈61 см) рефрактор болды, бұл аспапта галактикалардың жақсылап көрсетілген көріністерін алу қиын болатын. Осы мәселені шешу мақсатында, Х. Шепли 1927 жылы жаңа классификация ұсынып, әлсіз галактикаларды классификациялауда туындайтын қиындықтарды ескеруге тырысты.

Гарвард классификациясында барлық галактикалар 5 класқа бөлінді:

А класы - 12m -ден жарық галактикалар
B класы - 12m -ден 14m-ке дейінгі галактикалар
С класы - 14m -ден 16m-ке дейінгі галактикалар
D класы - 16m -ден 18m-ке дейінгі галактикалар
E класы - 18m -ден 20m-ке дейінгі галактикалар

Едеуір көмескі галактикалар Гарвард обсерваториясында бақылау үшін қолжетімсіз болды, алайда қажет болған жағдайда жүйе одан әрі кеңейтілуі де мүмкін.

Галактиканың әрбір класының іші екі параметрмен сипатталды: шоғырлану және эллипстілік. Барлығы болып 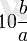$10\frac{b}{a}$ формуласына сәйкес эллипстіліктің 10 градациясы енгізілді, мұнда a және b - галактика пішіні жазылатын эллипстің үлкен және кіші жартылай өстері. Алынған мән бүтін санға дейін дөңгелектенеді. Сөйтіп, «дөңгелек» галактика 10 эллипстік индексін, ал ұршық тәріздісі - 1 индексін иеленді. Шоғырлануға дейін орталығына шоғырлану дәрежесінің ұлғаюына қарай a , b , c , d , e , f кіші латын әріптерімен белгіленетін 6 градация енгізілді. Егер мүмкін болса, шоғырлану дәрежесі фотометрикалық тұрғыдан, кері жағдайда «жай көзбен» өлшенді.

Егер галактикаларда спиральды құрылым көрініп тұрса, осындай галактикалардың классификациясына s индексі қосылып отырды. Пішін мен шоғырлануының тұрақсыздығы i индексімен атап өтілді.

Сөйтіп, Df 2 галактикасы - 16-18m диапазонындағы көмескі галактика, орталығына қарай қатты шоғырланған және қатты созылған, sAb 9 - дөңгелек дерлік, беткейі біртегіс жарық болып келетін жарық спиральды галактика.

Осы классификацияға жататын объектілер саны оны жасау кезеңінде онша үлкен болған жоқ. Олар үшін жеке сипаттама мүмкіндігі берілді.

Келтірілген жүйені біршама уақыт бойы Гарвард обсерваториясы белсенді пайдаланып келді, алайда ол Хабблдың едәуір табысты классификациясы тарапынан ығыстырылып шығарылды.

1. 1. 2 Хаббл реттілігі

1. 1 сурет - Хаббл камертоны

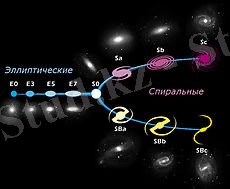
Хаббл реттілігі - бұл 1926 жылы Эжвин Хаббл ұсынған және 1936 жылы өзі өзгерткен морфологиялық классификация, ол Хаббл камертоны атауымен белгілі, өйткені осы реттіліктің дәстүрлі көрінісі осы аспапқа ұқсас болып келеді.

Өз классификациясында Хаббл (В) көк сүзгіде экспозицияланған фтотграфиялық пластинкалардағы олардың сыртқы түріне негізделе отырып, барлық галактикаларды 3 кең класқа бөледі.

1. 2 сурет - M49 ( E 2) эллипстік галактика

Эллипстік галактикалар ерекше бөлшектері жоқ, орталығынан шетіне қарай жарығы біртегіс азая түсетін жазық эллипстік пішінге ие (дөңгелек күйге дейін қатты майысқан) . Олар Е әрпімен және галактикалардың майысу индексіне ие цифрмен таңбаланады. Мәселен, дөңгелек галактика E 0 белгісін, үлкен жартылай өстерінің бірі екіншісінен екі есеге үлкен галактика E 5 деп таңбаланады. «Майысу индексі» мәні 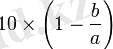$10 \times \left(1-\frac{b}{a}\right)$ формуласымен есептеледі, мұнда a және b - көрінетін эллипстің үлкен және кіші жартылай өстері. Едеуір майысқандардың ( E 7) пішіні эллипстен біршама ерекшеленеді. Эллипстік галактикалар ескі жұлдыздардан құралып, газдан толық айырылған.

1. 3 сурет - М81 ( Sb ) спиральды галактика

1. 4 сурет - NGC1300 ( SBbc ) - «қолшасы» бар спиральды галактика.

Спиральды галактикалар жұлдыз бен газдан құралған жалпақ дискіден (оның ортасында балдж деп аталатын сфералық нығыздауыш орналасады), сонымен қатар кең сфералық галодан тұрады. Диск жазықтығында көбіне жас жұлдыздардан, газ бен тозаңнан тұратын ашық спираль жеңдер құрылады. Хаббл барлық белгілі спираль галактикаларды қалыпты спиральдарға (S символымен белгіленеді) және бары бар спиральдарға ( SB ) бөледі, оны отандық әдебиетте тосқауылды немесе қиылысқан деп жиі атайды. Қалыпты спиральдарда спиральдық бұтақтар тангенциалды түрде орталық ашық ядродан алыстап, бір айналым ұзақтығында жайылады. Бұтақтар саны түрліше болуы мүмкін: 1, 2, 3, … бірақ галактикалар көбіне екі бұталы болып кездеседі. Қиылысқан галактикаларда бұтақтар бар ұшынан тік бұрышпен таралады. Олардың арасында екі бұтаққа тең келмейтін бұтақтар саны кездеседі, негізгі массада қиылысқан галактикалар екі спиральдық бұтақтарға сай келеді. Спиральды жеңдер тығыз бұралғанына немесе ядро мен балдждың мөлшерлері қатынасы бойынша жұмырлануына қарай a , b немее c символдары енгізіледі. Мәселен, Sa галактикаларына үлкен балдж және қатты бұралған тұрақты құрылым тән, ал Sc галактикаларына кішігірім балдж және жұмырланған спиральды құрылым тән. Sb класс тармағына әлдебір себепке байланысты шеткі класс тармақтарының біріне жатқызуға болмайтын галактикалар кіреді: Sa немесе Sc . Мәселен, M 81 галактикасы үлкен балдж бен жұмырланған спиральды құрылымға ие.

1. 5 сурет - NGC1427A - дұрыс емес галактика

Дұрыс емес немесе тұрақсыз галактикалар - айналу симметриясынан және маңызды ядросынан айырылған галактика. Магеллан бұлттары дұрыс емес галактикаларға тән өкіл болып танылады. «Магеллан тұмандылығы» деген термин де бар. Дұрыс емес галактикалар пішіндерінің алуан түрлі болып келуімен, кішігірім өлшемімен және тозаң мен жас жұлдыздардың мол болуымен ерекшеленеді. I деп белгіленеді. Дұрыс емес галактикалардың пішіні нақты анықталмағандықтан, дұрыс емес галактикаларды көбіне пекулярлық галактикалар деп атаған.

Галактикалар классийикациялау үшін тым көмескі болып табылатындықтан, Хаббл Q символымен белгіледі.

1936 жылы құрылысы спиральды галактикаларға ұқсас, бірақ спиральды құрылымы жоқ Линза тәрізді галактикалар қосылды. S0 белгіленді. Егер линза тәрізді галактикалар жанынан көрініп тұрса, ол эллипстік галактикадан қатты қысылуымен және күңгірт тозаң қабаты болуымен ерекшеленеді.

1. 1. 3 Хабблдың қайта қаралған реттілігі

1935 жылдан бастап 1953 жылы қайтыс болғанына дейін Хаббл өз жүйесін жақсартумен шұғылданды. Хабблдің ісін оның әріптесі А. Сендидж жалғастырды, ол 1961 жылы Хаббл реттілігін қайта қарап шығуды аяқтады. Хабблдың жаңартылған реттілігінің негізгі жаңалықтары:

1. 6 сурет - Ұршық галактикасы ( S 0)

Линза тәрізді галактикалар класы қосылды ( S 0 және SB 0) . Осы галактикалар эллипстіктік галактикадан спиральды галактикаларға өтпелі класс болып табылады. Олар ашық, жақсы көрініп тұратын ядросы және азды-көпті біртекті дискі немесе линзасы, дискіден тыс аумақты қадағалайтын диффузиялық қабықшаға батырылған айқын шекарасы бар линзасы болуымен сипатталады. Спиральды бұтақтары жоқ.

S 0 галактикалары екі типке бөлінеді:

1) S 0(1) - диск пен қабықшада құрылымы жоқ (NGC1201, NGC1332) ;

2) S 0(2) - күңгірт аумақтар мен сақина пішінді қабықшада басталған құрылымға ие. Жанынан қарағанда, сақиналар ілмек тәрізді көрініп тұрады, мұның өзі осы галактикаларды Сатурнмен ұқсас етеді (NGC4459, NGC4111) . Сонымен қатар S 0/ a өтпелі сыныбы ерекшеленіп тұрады. Мұндай кластағы галактикаларда қабықшасында туындап келе жатқан спиральды құрылымдар байқалады.

SB 0 галактикаларында линзаны қиып өтетін бар көрініп тұрады; кейде кең әрі айқын емес, кейде тар және айқын. Қабықшаның ішінде сақина қалыптасуы мүмкін. Хаббл осы галактикаларды 3 топқа бөлді:

1) SB 0 (1) - үлкен, көмескі, құрылымсыз қабықшамен қоршалған, кең және айқын емес бары бар жарық линзалар (NGC3384, NGC4203) ;

2) SB 0 (2) - әлсіз кең бар және қабықшадағы бір сақина (NGC2859) ;

3) SB 0 (3) - жақсы көрініп тұратын бар және сақина (NGC4653, NGC5101) .

Бұрын SBa ретінде классификацияланған галактикалардың көпшілігі SB 0 класына өткізілді. SBa класын анықтау барынша қатаң бола бастады: осы кластағы галактикалар жылтыр барға және әлсіз дамыған, қатты байланған спиральды жеңдерге ие.

Қиылысқан спиральдар топтарға бөлінді ( SBa және SBb кластарының галактикалары кірді) : Галактикалардың жеңдері бар қиып өткен сақинаның шетінен басталады (NGC2217 ( SBa ), NGC5950 ( SBb ) ) ; Галактикалардың жеңдері бар ұштарынан басталады (NGC4290 ( SBa ), NGC6951 ( SBb ) ) ;

Сендидж сонымен қатар кәдімгі спиральдарды топтарға бөлді:

1) cпиральды жеңдері сақинаның сыртқы шетінен басталатын галактикалар;

2) cпиральды жеңдері ядродан басталатын галактикалар.

Күрделі, жұлым тәрізді құрылымға және әлсіз айқын ядроға ие, төмен беткейлі жарқылы бар спиральды галактикалар үшін сәйкес ретте кәдімгі және қиылысқандарға арнап Sd және SBd таңбалары енгізілді. Спиральға ұқсастарды айқындау мүмкін болған дұрыс емес галактикалар үшін Sm таңбасы енгізілді.

1938 жылы Мүсінші және Пеш шоқжұлдыздарынан Шепли ашқан ергежейлі эллипстік галактикалар ( dE ) класы енгізілді. Осы галактикалар беткейлік жарығының тым төмен болуынан басқа, қарапайым эллипстік галактикалардың барлық морфологиялық қасиеттеріне ие.

Жалпы алғанда, Хаббл реттілігі галактикалардың алуан түрлі қасиеттерін қамтиды: газ бен тозаң жоқ, жұлдыз жасалымы жоқ және басты құрамдас бөлігі - ескі жұлдыздар жоқ эллипстіктен құрылымының бұзылуына қарай газ, тозаң және жас жұлдыздар үлесі ұлғая түсетін линза тәрізді және спиральды галактикалар арқылы тозаңның мөлшері көп болуынан жұлдыз жасалымының жоғары қарқыны орын алатын дұрыс емес галактикаларға. Хабблдың өзі осы реттілікті эволюциялық реттілік деп атайды, мұның өзі кейінгі зерттеулерде расталған жоқ.

Қазіргі таңда Хаббл реттілігі кәсіпқойлар тарапынан да, әуесқой астрономдар тарапынан да галактикаларды классификациялау үшін барынша қажет болып отыр.

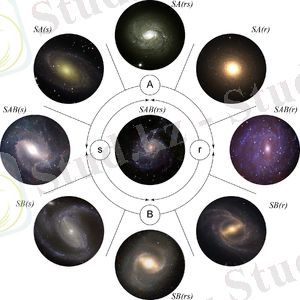
1. 1. 4 Ж. де Вокулёр жүйесі

1. 7 сурет - Ж. де Вокулёр жүйесінің үшөлшемді көрінісі

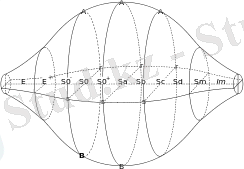
Ж. де Вокулёр жүйесі - бұл 1959 жылы де Вокулёр ұсынған Хаббл жүйесінің кеңінен қолданылатын жүйесі.

Маунт Стромло (ағылш. Mount Stromlo) обчерваториясында өткізілген оңтүстік аспан галактикаларын зерттеу бойынша жұмыстарға негізделе отырып, Ж. де Вокулёр Хаббл классификациясын барынша негізді етіп қайта өңдеуге тырысты. Өз жұмысында ол А. Сендиджбен жеткілікті шамада тығыз өзара әрекеттесті, мұның өзі олардың шешімдері кейбір тұстарда сәйкес келетіндігін көрсетті. Ж. де Вокулёр спиральды галактикалардың барға ие және барға ие емес деп бөлінуі спиральдырдың морфологиялық ерекшеліктерінің диапазонын жеткілікті шамада жақсы көрсете алмайтынын Хаббл классификациясының негізгі кемшілігі деп санайды. Атап айтсақ, де Вокулёр сақина және балдж сияқты спиральды галактикалардың құрылымдық ерекшеліктерін көрсетті.

Өз жүйесінің негізінде де Вокулёр Хабблдың галактикаларды эллипстік, линза тәрізді, спиральды және дұрыс емес деп бөлуін сақтап қалды. Эллипстік галактикалардың классификациясы өзгеріске ұшыраған жоқ. Негізгі өзгерістер спиральды галактикалар классификациясын, аз шамада линза тәрізді және дұрыс емес галактикалар классификациясын қамтыды.

Едеуір жеткілікті статистика жинақталу нәтижесінде, бары бар галактикалар саны бары жоқ галактикалар санымен мөлшерлес болып шықты. Сондықтан бары жоқ галактикаларды қалыпты жайт деп айту (ағылш. normal spirals) мүлдем дұрыс емес. Де Вокулёр оларды қарапайым (ағылш. ordinary spirals) деп атап, SA -мен белгіледі, ал бары бар спиральды галактикалар (ағылш. barred spirals) өзінің SB блегісін сақтап қалды. Сөйтіп, бары бар спиралдарға қарағанда, қарапайым спиралдар онша қалыпты болып саналмайды. SA , сонымен қатар SB қасиеттеріне ие галактикалар SAB өтпелі класына жатқызылды. Дәл классификациялау мүмкін болмаған спиральды галактикалар (нашар шешіміне, көз нұрына қатты иілуіне орай және т. б. ) жай ғана S -пен белгіленді.

Линза тәрізді галактикалар да осындай өзгерістерге түсті: бары жоқ галактикалар SA 0 белгісін, бары бар галактикалар - SB 0 белгісін, өтпелі типі - SAB 0 белгісін алды. S 0 белгісі классификацияланбаған галактикалардың еншісіне тиді.

Спиральды және линза тәрізді галактикалардың аталған топтары де Вокулёр бойынша спиральды немесе сақина тәрізді түрді қабылдайтын (галактика орталығының айналасында спиральды бұтақтар тарайтын сақина бар) әлдебір пішіндегі құрылымға ие. Галактикалардың сақина тәрізді түрлері ( r ) индексін, ал спиральды түрлері ( s ) индексін алды. Кейбір өтпелі түрлер үшін ( rs ) таңбасы енгізілді. Сақина тәрізді галактикаларда сақиналар ішкі және сыртқы болып келеді. Сыртқы сақиналар үшін ( R ) индексі енгізілді.

1. 8 сурет - Жерар Анри де Вокулёр классификациясына арналған галактикалар үлгісі

1. 2. 1 Фракталдар.

Табиғатта кездесетін өлшемдері атомдық масштабтан әлемдік кеңістікке дейін созылып жатқан обьектілердің (нысандардың) геометриясы біздің оны зерттеп түсіну үшін құратын, идеалдандырылған модельдерімізде басты орын алады. Бірақ дәстүр бойынша табиғат геометриясын индуктивті түсінудің негізі ретінде осы уақытқа дейін евклидтік геометрияның түсініктері: сызықтар, шеңберлер, сфералар мен тетраэдрлар қолданылады.

Күрделі жүйелерде болатын процестерді, құрылымды - стохастикалық құбылыстарды барынша қарапайым түрде сипаттауға, түсіну мен түсіндіруге мүмкіндік беретін ғылым - фракталдар теориясы.

Фрактал түсінігі алғаш математикалық түрде күрделі геометриялық формаларды сипаттау үшін енгізіледі. Ғылымның дамуы және компьютерлік техниканы қолданудың алуан түрлі мүмкіндіктері фрактал түсінігінің табиғаттың ең жалпы, түбегейлі заңдылықтарымен байланысты екенін көрсетті. Физика - математика ғылымдарының бұл жаңа бағытының күрт дамуына француз ғалымы Б. Мандельброттың 1982 жылы жарық көрген "Табиғаттың фракталдық геометриясы" атты кітабының шығуы тікелей себеп болды.

Б. Мандельброт бұл кітабында табиғатта кездесетін фракталдық нысандардың көптеген мысалдарын келтірді және оған ғылыми көпшіліктің жаппай назарын аударды. Оның дамытқан геометриясы сан түрлі обьектілердің формасын сипаттауға қолданылуымен қатар, заңдылығы бар, масштабты - инварианты құрылымдарның моделін салуға мүмкіндік береді. Осы үлгілерді қолдану ретсіз құрылымдарды зерттеп білудің жаңа жолдары болып табылды.

Аспандағы бұлттар, тау сілемдері, терезе шынысына қатқан қыраулар, полимерді түзетін молекулар, тірі клеткалар және тағы сол сияқты нысандар мен құрылымдардың бәріне ортақ бір қасиеті - олардың кіші және бөліктерінің бір - біріне ұқсастығы. Әртүрлі уақыт мезетінде түсірілген, үлкен және кіші бұлттардың суреттерін салыстыру олардың өзгеру заңдылығының бірдей болатынын көрсетеді. Осы сияқты заңдылықты әртүрлі масштабта түсірілген жағалау сызықтарының фрагменттерінін (мысалы, Британия аралының, Арал теңізінің, Балқаш көлінің) салыстыру арқылы да байқауға болады.

Осындай өзұқсас нысандар үшін француз математигі Б. Мандельброт жаңа фрактал (латыншадан аудармасы - бөлшектік, кескіленген) ұғымын енгізді. Ол құрылымдық, өзіне - өзі ұқсас иерархиялық ішкі құрылысы бар обьектілерді фракталдар деп аталады. Фракталдық қасиет бейсызық процестер мен құбылыстарды сипаттайтын фазалық кеңістіктерде, күрделі жүйенің функционалды харакеттерінде, адрондардың әсерлесуінің, қоғамның экономикалық көрсеткішінің өзгерістерінде және т. б. байқалады.

Фракталдардың дәл және қатаң анықтамасы әзірге жоқ. Б. Мандельброт алғаш рет фрактал анықтамасының мынадай вариантын ұсынған: фрактал деп тұтас күйіне белгілі бір мағынада ұқсас бөліктерден тұратын құрылым айтылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.